引言

随着数字技术、通信技术的飞速发展与普及, 图像信息成为多媒体和网络中最重要的信息之一. 然而, 由于互联网的不确定性与开放性, 在图像数据传输过程中, 其信息数据安全性问题越来越受到重视. 所以, 如何保证数字图像的安全性显得特别重要, 图像加密是最直接有效的途径之一. 传统的加密方法加密效率低、时间较长, 不再适用于图像加密^[1,2]. 由于混沌系统具有伪随机性、初值敏感性等特性, 因此将混沌系统应用到图像加密中非常契合. 随着研究的不断深入, 混沌图像加密算法和技术有了相当大发展^[3–6].

文献[7]提出基于logistic映射图像加密算法. 简单易实现, 效果良好, 但是单一的映射加密安全性较差. 文献[8]提出一种基于图像分区的置乱算法. 该算法首先对原始图像进行分块置乱,再对相邻像素值进行异或运算置乱图像. 谢国波^[9]提出了结合logistic映射和Arnold映射对图像进行加密, 提高了置乱和扩散两者之间的关联性, 增加了图像的安全性. 文献[10]提出了加强型超混沌加密算法, 相比低维系统密钥空间大, 非线性行为复杂化, 虽提高了图像的安全性, 但是效率不高^[11–13].

本文在cubic映射和logistic映射基础上, 提出了一种改进logistic映射的图像加密算法. 首先改进logistic映射对图像进行置乱, 然后将置乱图像进行相邻像素间按位异或运算、交叉换位操作, 实现了对数字图像的加密. 实验结果表明, 本文算法不仅达到了较好的加密效果, 而且安全性好, 抵抗统计攻击和差分攻击强等特点.

1 Logistic映射及改进 1.1 Logistic映射

Logistic映射是一个典型的非线性迭代方程. 其方程如下:

${x_{k + 1}} = \mu {x_k}(1 - {x_k})$

(1)

其中, 当3.5699< $\mu $ ≤4时, Logistic映射系统处于混沌状态, 对给定初始值 ${x_0}$ , 在式(1)作用下生成的序列是非周期性、非收敛以及对初始条件敏感的, 如图1所示.

1.2 改进的Logistic映射

目前一维离散混沌映射有logistic映射和cubic映射以及它们的衍生映射, 其共同点都是系统参数少, 混沌区间窄, 混沌的复杂性较低, 函数形式简单. 为了克服以上不足, 本文将logistic映射和cubic映射进行结合改进, 其方程表达式如下所示:

$ \left\{ {\begin{array}{*{20}{c}} {{x_{k + 1}} = \mu {y_k} - c{x_k}{y_k}} \\ {{y_{k + 1}} = ax_k^2 - b{x_k}} \end{array}} \right. $

(2)

式中, $\mu \in [0,4]$ , $a \in [0,4]$ , $b \in [0,3]$ , $c \in [0,4]$ 当参数 $\mu $ =1.8, a=0.5, b=1, c=1时, 系统具有两个正的Laypunov指数, 说明该系统是一个超混沌系统.

为了检验改进logistic映射系统伪随机性的好坏, 分别对logistic映射改进前后进行了NIST测试, 测试结果如表1所示, 从表1可以看出, logistic序列有5项密钥通过, 改进logistic映射全部通过, 表明改进后映射的伪随机性高于经典的logistic映射.

2 改进的加密算法设计 2.1 位置置乱

本文应用改进的logistic映射置乱明文图像, 其主要步骤如下:

(1) 将原始明文图像转换成二维矩阵, 分别将其行数和列数放在数组C1和C2中;

(2) 计算原始明文图像所有像素值之和为sum, 通过式(3), 得到辅助密钥k;

$ k = od (sum,256)/255 $

(3)

(3) 设改进logistic映射的初始值为 ${x_0}$ 和 ${y_0}$ 经过 ${x'_0} = \sqrt {({x_0}^2 + {k^2})/2} $ 和 ${y'_0} = \sqrt {({x_0}^2 + {k^2})/2} $ 得到混沌系统新的初始值 ${x'_0}$ 和 ${y'_0}$ ;

(4) 设置初始条件 ${x_0}$ =0.3, ${y_0}$ =0.4经过式(2)迭代生成两个实数序列 $\left\{ {{x_k},{y_k}|k = 1,2,\cdots, m \times n} \right\}$

(5) 对序列 ${x_k}$ 和 ${y_k}$ 分别依次进行升序操作, 并相应地记录各元素在原始序列的下标, 得到两个序列的索引Index1和Index2, 将索引Index1和Index2与原始图像的行C1和列C2交换, 从而达到置乱的效果, 得到置乱图像C.

2.2 图像像素值的改变

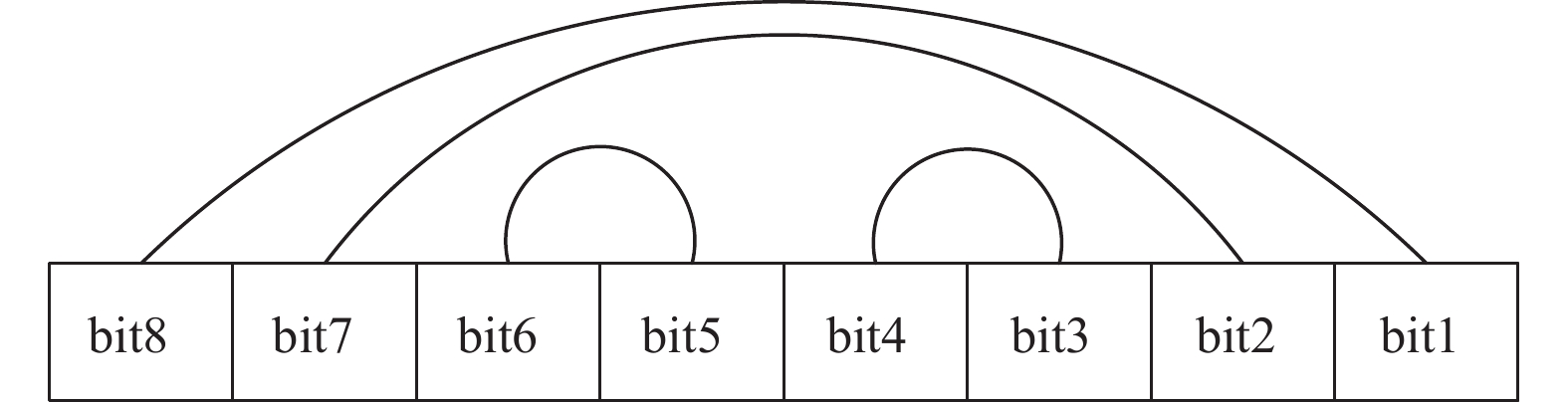
首先对置乱图像C中每个像素和它前面相邻的像素进行按位异或运算, 再对其异或运算的结果进行像素值的交叉换位, 得出最终加密图像. 其主要步骤如下:

(1) 设置乱图像C的第一个像素的灰度值为C(1)与255进行异或, 得到 $C'(1)$ ,再对 $C'(1)$ 进行交叉换位, 得到Q(1). 具体的换位操作如下图2所示(图 2中的bit1, bit2, …, bit8 分别表示像素点二进制灰度值的第 1, 2, …, 8位);

(2) 置乱图像C的第二个像素的灰度值C(2)与Q(1)进行异或操作, 得到 $C'(2)$ ,再对 $C'(1)$ 进行交叉换位, 得到Q(2);

(3) 依次将图像的每个灰度值C(i)与Q(i-1)进行异或, 得到 $C'(i)$ ; 依据交叉换位规则得到Q(i). 最后将一维Q(i)换成图像D, 即得到最终加密图像D.

2.3 解密算法

解密过程为加密过程的相反过程, 只要在正确的密钥条件下, 按照加密过程的相反操作处理就可以恢复得到原始图像.

3 仿真结果

本文采用经典的Lena作为原始图像, 大小为256×256, 在 Matlab7.0平台上仿真实验, 运行得到加密图像. 图3(b)为置乱图像, 图3(c)为密文图像, 图3(d)为正确解密图像.

4 算法分析 4.1 直方图分析

图4(a)为明文图像的灰度直方图, 图4(b)为密文图像的灰度直方图. 从图4可以看出, 明文图像的像素点分布不均匀, 密文图像的像素点分布相对均匀, 很好地隐藏了明文图像的统计特性, 达到了预期的要求.

4.2 密钥空间分析

本文加密算法中改进的logistic映射有4个系统参数和2个初始值共6个密钥值. 假如计算机精度可以达到 ${10^{ - 16}}$ ,那么密钥空间为 ${10^{96}}$ ,以及在置乱-扩散过程中有一个外层循环, 可见密钥空间非常大. 想要通过穷举攻击解密图像, 成功的几率是及其渺小的, 也就是说可以满足抵御暴力破译的要求.

4.3 信息熵

信息熵是衡量信号源不确定性的重要参数, 图像越是混乱, 信息熵就越接近理想值, 其定义式为:

$ H(m) = \sum\limits_{i = 1}^{2N - 1} {P({m_i})} {\log _2}\frac{1}{{P({m_i})}} $

(4)

其中, $P({m_i})$ 是灰度值 ${m_i}$ 出现的概率, N为像素比特位数. 由式(11)计算可得原始图像的信息熵为7.5683, 密文图像的信息熵为7.9900, 非常接近于灰度级为256的图像最大值8, 可以得出密文图像所有像素值分布十分均匀的, 加密系统能够有效地抵御恶意熵攻击.

4.4 相邻像素点的相关性

为了检验与分析加密前后图像的相关性, 分别从明文和密文中随机性地选取2000对相邻的像素, 使用式(12)计算相关性:

$\left\{ {\begin{array}{*{20}{l}} {D(x) = 1/n\sum\limits_{i = 1}^n {{{[{x_i} - E(x)]}^2}} } \\ {\operatorname{cov} (x,y) = 1/n\sum\limits_{i = 1}^n {[{x_i} - E(x)][{y_i} - E(y)]} } \\ {r = \operatorname{cov} (x,y)/(\sqrt {D(x)} \sqrt {D(y)} )} \end{array}} \right.$

(5)

其中, E(x)、E(y)分别是x, y的期望; n是像素点的个数; cov(x, y)是x, y的协方差; r相关系数,

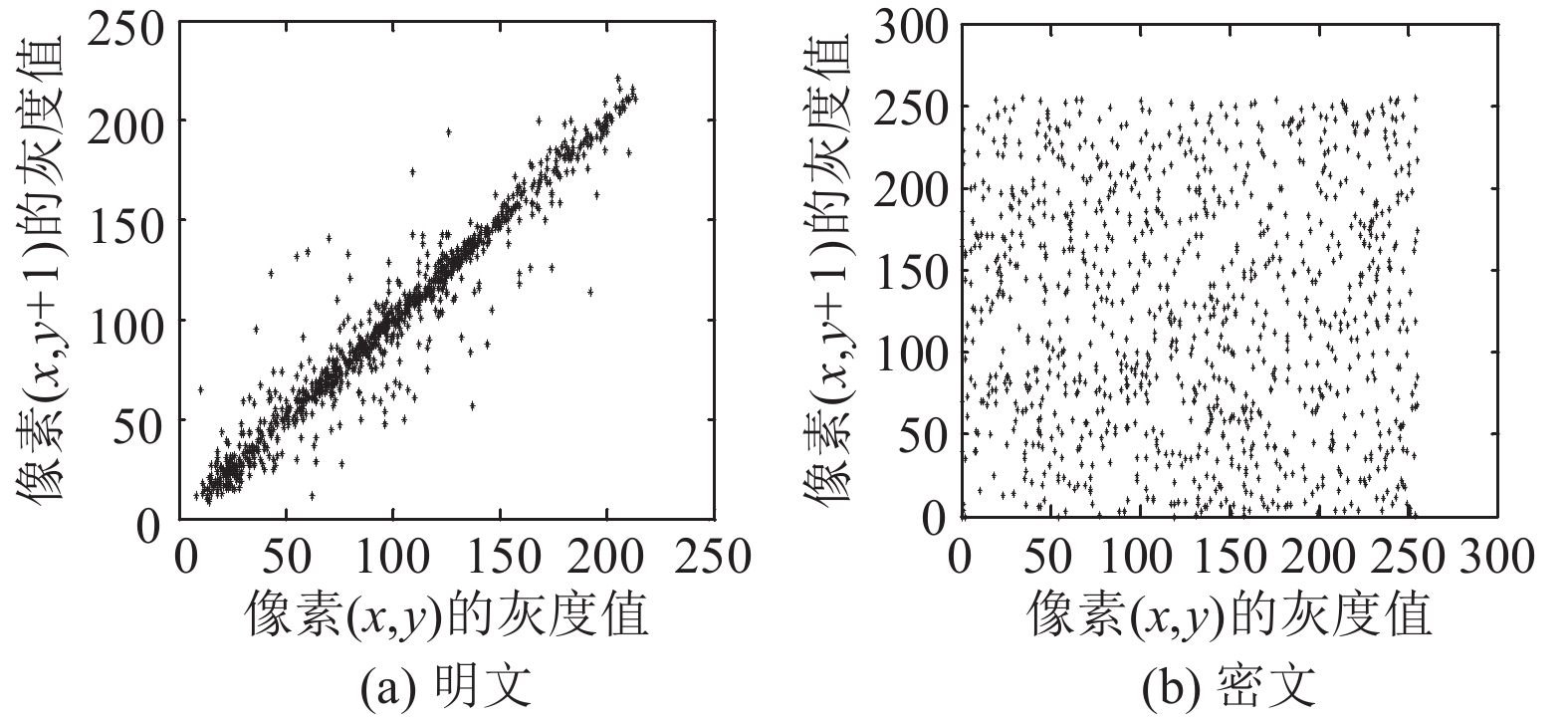
图5至图7分别是明文图像和密文图像在垂直、水平、对角线方向相邻点分布情况. 从各图中可以看出, 明文图像中的点基本上都集中在对角线周围, 即图像相邻点相关性很强. 而密文图像中的像素点均匀集中在坐标上, 即密图相邻点相关性低.

由表2可得到, 明文图像的相邻像素点相关性系数趋近于1, 而密文图像的相关性较小, 其相关系数靠近于0, 可以得出密文图像的相邻间像素点基本不再相关. 相比较其他算法^[4,9,14], 可见该算法的相关系数r更小一点, 说明本文加密算法具有良好的扩散性.

4.5 差分攻击分析

为了测试明文图像一个像素的变化对该算法整体加密结果的影响, 采用两种常见的措施^[15]: 像素变化率(NPCR)和统一平均变化程度(UACI). 若一个像素值的变化导致密文图像发生显著地改变, 就可以说明算法能抵御差分攻击.

$NPCR = \frac{{\sum\limits_{i,j} {D(i,j)} }}{{m \times n}} \times 100\% $

(6)

$UACI = \frac{1}{{m \times n}}\left[ {\sum\limits_{i,j} {\frac{{\left| {{C_1}(i,j) - {C_2}(i,j)} \right|}}{{255}}} } \right] \times 100\% $

(7)

其中, ${D_{ij}} = \left\{ {\begin{array}{*{20}{c}} {1,{c_1}(i,j) \ne {c_2}(i,j)} \\ {0,{c_1}(i,j) = {c_2}(i,j)} \end{array}} \right.$ , m和n分别是图像的行数和列数;

现从图像中随机选取5个像素点, 分别将像素值加1, 再对改变像素值后图像进行加密, 应用式(13)和式(14)进行计算. 对得到的值取平均值NPCR= 99.61%和UACI=31.62%. 这就说明当改变原始图像lena(256×256)一个像素时, 会使密文图像接近100%的NPCR变化, UACI也在31%以上. 说明本文加密算法抵抗差分攻击能力比较强.

5 结束语

本文提出了基于改进logistic映射的图像加密算法. 先利用改进的logistic映射对图像进行位置置乱, 再进行相邻像素间按位异或、交叉换位操作得到最终加密图像. 仿真实验分析表明, 该算法可以达到良好的加密效果、简单易实现、安全性较好, 在数字图像通信传输中, 具有良好的实用价值.