2. 商洛学院 经济管理学院, 商洛 726000
2. Faculty of Economics and Management, Shangluo University, Shangluo 726000, China
随着数据采集技术和存储技术的发展, 获取大量无标记样本已经比较容易, 而由于需要耗费一定的人力和物力, 获取大量有标记样本则比较困难[1]. 如果只使用少量有标记样本, 采用有监督学习方法进行分类, 那么有监督学习训练得到的学习模型不具有很好的泛化能力, 同时造成大量无标记样本的浪费; 如果只使用大量无标记样本, 采用无监督学习方法进行分类, 那么无监督学习将会忽略有标记样本的价值. 因此, 研究如何综合利用包含少量有标记样本和大量无标记样本来提高学习性能的半监督学习(Semi-supervised Learning)成为当前机器学习非常重要的研究领域之一[1–3].
半监督学习[4,5]是一种介于传统有监督学习和无监督学习之间的新的机器学习方法, 其目的就是充分利用大量的无标记样本来弥补有标记样本的不足. 半监督分类主要研究从有监督学习的角度出发, 当有标记训练样本不足时, 如何利用大量无标记样本信息辅助分类器的训练. 目前的半监督学习方法大致有四种主流范型[6], 即基于生成式模型的方法、半监督SVM方法、基于图的方法和基于协同训练的方法. 半监督学习是当前的一个研究热点, 广泛应用到各种实际应用中, 且取得了较好的成果[1,4,5].
虽然半监督学习方法被成功应用于处理不同类型的数据集, 但是半监督学习过程中无标记样本的选择会增加算法的随机性, 同时传统的半监督学习对不同的参数值敏感, 会导致不稳定的结果, 这些都会影响半监督学习的鲁棒性[7–9].
集成学习可以减少由于无标记样本的随机选择导致分类器性能的下降. 与单一的半监督学习方法相比, 半监督集成学习方法能够将从不同数据集中生成的多个学习模型产生的结果进行集成, 得到的结果更准确、更稳定, 鲁棒性更强[7,8]. 已有不少学者从事半监督集成学习方面的研究, 且取得了较好的研究成果. Zhou和Li[10]对标准的协同训练算法Co-training进行改进, 提出了一种既不要求充分冗余视图、也不要求使用不同类型半监督分类器的tri-training算法. Mallapragada等人[11]将Boosting技术推广到半监督学习中, 提出了Boosting的半监督版本SemiBoost. Yaslan和Cataltepe[12]利用随机子空间技术研究自学习半监督学习. Yan等人[13]提出了一种有效的鲁棒半监督集成学习方法处理带有噪声标签的大规模数据集. Stanescu和Caragea[14]将半监督集成学习方法应用到不平衡数据集的分类领域. Yu等人[15,16]提出了一种渐进子空间集成学习方法. Ding等人[16]提出一种高效的半监督聚类集成算法. Liu等人[17]提出了一种基于稀疏特征空间表示的半监督多源自适应学习框架. Yu等人[18]提出一种增量式半监督聚类集成方法和一种基于选择约束投影的半监督集成聚类.
但是, 传统的半监督集成学习方法仍然存在下面几个局限性:
(1)很少考虑如何处理高维且具有极少量有标记样本的数据集[7,18].
(2) 大多数集成方法在处理一些高维数据时, 只考虑样本空间中数据的分布, 或者特征空间中属性的分布. 没有将这两种分布综合起来进行处理, 以获得更好的结果[15].
将样本空间中数据的分布和特征空间中属性的分布两者综合起来, 实现高维数据的分类, 能有效改善分类性能. 一方面能有效的缩减问题的规模, 缩短分类时间, 另一方面能有效选取对分类贡献大的属性和样本参与分类, 提高分类效率, 改善分类性能[15].
本文从探索数据样本空间和特征空间两个角度出发, 提出一种结合随机子空间技术和集成技术的安全半监督学习算法(A safe semi-supervised learning algorithm combining stochastic subspace technology and ensemble Technology, S3LSE), 处理仅包含极少量有标记样本的高维数据分类问题. 首先, S3LSE采用随机子空间技术将高维数据集分解为B个特征子集, 并根据样本间的隐含信息对每个特征子集优化, 形成B个最优特征子集; 接着, 将每个最优特征子集抽样形成G个样本子集, 在每个样本子集中使用安全的数据样本标记方法扩充有标记样本, 生成G个分类器, 并对G个分类器进行集成; 然后, 对B个最优特征子集生成的B个集成分类器再次进行集成组合, 实现高维数据的分类. 最后, 使用高维数据集模拟半监督学习进行实验, 验证算法的有效性.
2 提出的算法算法S3LSE充分利用高维数据特征之间的关系, 挖掘高维数据之间的隐含信息, 扩充有标记高维数据的数目. 主要通过将高维数据的分类问题转化为低维数据的分类问题. 通过对新增标记进行可靠性验证的方法, 保证新增标记样本的增加后, 分类器的性能不会恶化, 分类器向着误差减小的方向进行演化. 同时, 通过多分类器集成的方法, 提高分类器的鲁棒性.
算法S3LSE的输入是训练集Tr, 包括无标记数据集Tu和有标记数据集Tl, 其定义如下:
| $ {{{T}}_r} = {T_u} \cup {T_l} $ | (1) |
| $ {T_l} = \{ ({x_1}, {y_1}), ({x_2}, {y_2}), \cdots, ({x_l}, {y_l})\} $ | (2) |
| $ {T_u} = \{ {x_{l + 1}}, {x_{l + 2}},\cdots, {x_{l + u}}\} $ | (3) |
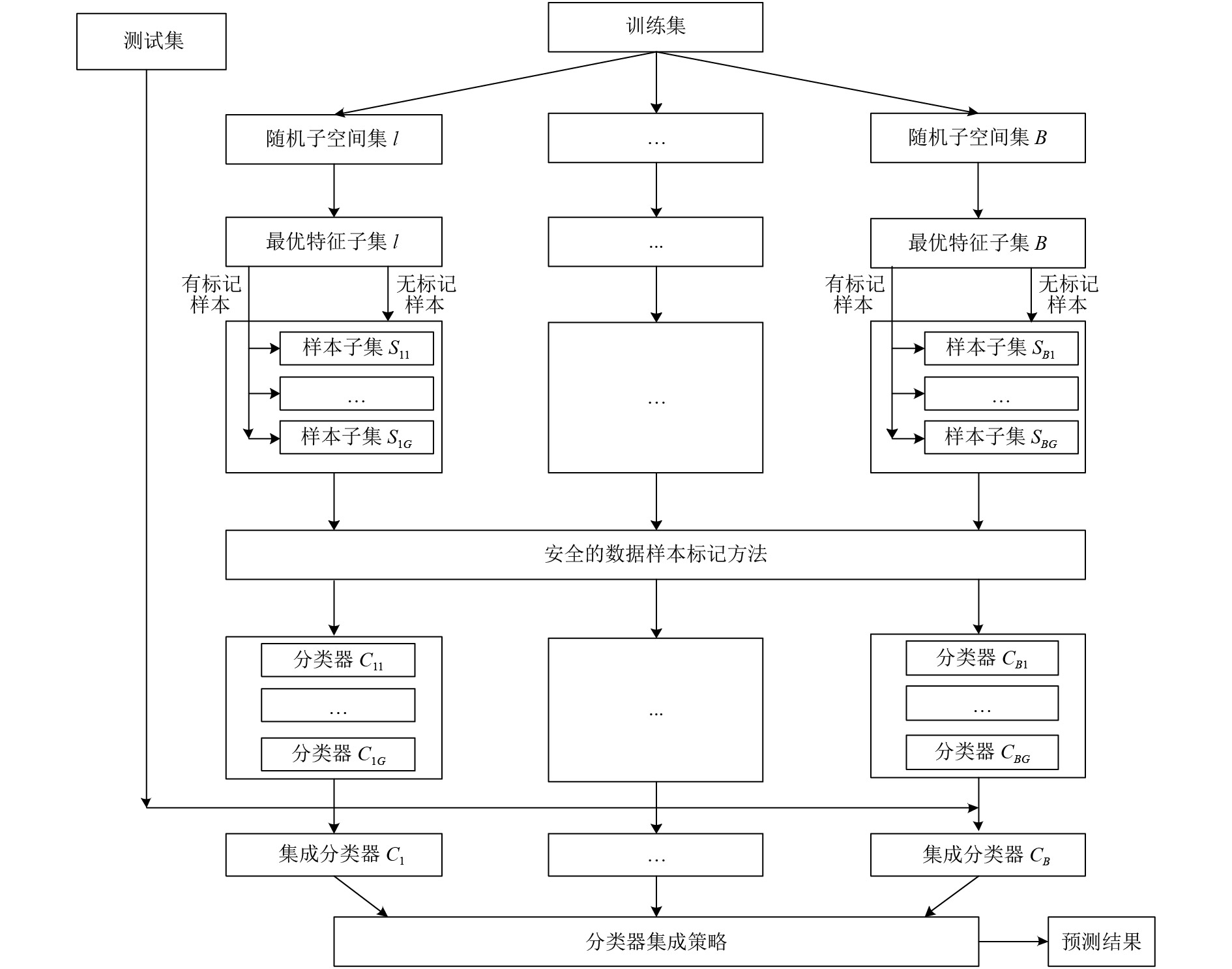
算法S3LSE流程如图1所示, 首先, 采用随机子空间技术将高维数据集Tr分解为B个特征子集, 并挖掘样本间的隐含信息, 对每个特征子集进行特征优化, 形成最优特征子集; 接着, 对每个最优特征子集进行抽样生成G个样本子集, 在每个样本子集中使用安全的半监督学习算法生成G个分类器, 并对G个分类器进行集成; 最后, 对B个最优特征子集中的形成的B个集成分类器再次进行集成, 挖掘高维数据的隐含信息, 实现高维数据的分类. 具体步骤如下:
|
图 1 算法流程图 |
(1)使用随机子空间技术进行特征子集划分
假设每个样本的特征数目为m, 特征选取率为τ, 随机子空间的特征数目为τ*m. 被选中的特征的序号为:
| $ j = \left\lfloor {1 + \varsigma (m - 1)} \right\rfloor $ | (4) |
式中, j表示被选中的特征的序号,
在随机选择过程中, 每个被选中的序号对应的特征将会被记录, 避免重复采样, 同时被重复选中的特征直接被忽略. 上述操作反复进行, 直到τ*m个特征全部被选中. 选中的τ*m个特征对应的样本组成一个随机子空间集(特征子集). 完成一个特征子集的选择后, 其它B–1个特征子集依次进行. 在整个特征选择过程中, 记录每个特征子集所选中的特征序号.
(2)特征子集优化(Feature optimization, FL)
随机子空间技术选取的特征具有随机性, 不能很好的反映出特征之间的相关性等信息. 因此, 在这里, 我们进行特征优化操作. 建立一个包括特征和标签之间的相关性(即特征的相关性)、特征之间的冗余度等信息的目标函数, 通过计算对应于每个特征子集的目标函数的值, 得出每个特征子集的对应的最优特征值, 形成最优特征子集. 特征的相关性函数如式(5)所示, 特征之间的冗余度计算如式(6)所示, 构造的最优化函数如式(9)所示.
| $ {\gamma _1}(R) = \sum\limits_r^R {\frac{{\frac{{\sum\nolimits_{({x_i}, {x_j}) \in {\Omega _{ML}}} {{{({f_{ri}} - {f_{rj}})}^2}} }}{{\sum\nolimits_{({x_i}, {x_j}) \in {\Omega _{CL}}} {{{({f_{ri}} - {f_{rj}})}^2}} }}}}{{{{\left| d \right|}^2}}}} $ | (5) |
式中,
| $ {\gamma _2}(R) = \frac{{\sum\limits_{r, c}^R {I({f_r}, {f_c})} }}{{{{\left\| d \right\|}^2}}} $ | (6) |
| $ I({f_r}, {f_c}) = - \frac{1}{2}\log (1 - {\rho ^2}({f_r}, {f_c})) $ | (7) |
| $ \rho ({f_r}, {f_c}) = \frac{{\sum\nolimits_i {({f_{ri}} - \overline {{f_r}} )({f_{ci}} - \overline {{f_c}} )} }}{{\sqrt {\sum\nolimits_i {{{({f_{ri}} - \overline {{f_r}} )}^2}\sum\nolimits_i {{{({f_{ci}} - \overline {{f_c}} )}^2}} } } }} $ | (8) |
式中,
| $ \mathop {\min }\limits_R \Gamma (R) = ({\gamma _1}(R), {\gamma _2}(R)) $ | (9) |
通过对式(9)进行优化, 在每个随机子空间集中产生最优的特征子集.
(3)在最优特征子集内, 使用抽样技术进行样本子集划分
在最优特征子集中, 有标记样本的数目很少. 那么, 在进行随机抽样过程中, 有可能造成某个样本子集中没有抽取到有标记样本, 影响后面的半监督学习. 所以, 在每个最优特征子集的抽样过程中, 我们首先仅仅对无标记样本集TU进行不放回抽样, 形成G个无标记子集; 然后, 将有标记集Tl和G个无标记子集分别进行合并, 形成G个样本子集; 最后, 其它B–1个最优特征子集中, 依次类推. 考虑到算法的时间效果, 在多个最优特征子集中可以并发运行.
(4)使用安全的样本标记方法在样本子集内进行样本标记
每个最优特征子集对应的G个样本子集中, 分别使用安全的数据样本标记算法对无标记样本进行标记, 挖掘无标记样本的隐含信息, 扩充有标记样本的数目.
算法的主要思想是使用多个伪标记对无标记样本进行标记, 将具有伪标记的样本加入到有标记样本集中, 参与训练和测试, 将使分类器误差较小的伪标记作为无标记样本的最终标记[19].
算法的主要过程如下: ① 选取一个无标记样本集U, 按照不同的分类类别对U中的无标记样本分别进行伪标记; ② 将标记后的候选样本放入有标记样本集中, 将有标记集进行分组, 各组依次作为训练集和测试集进行组合, 使用训练集训练分类器, 在测试集上进行测试, 记录每次组合对应的误差, 将平均值作为每种伪标记对应的误差值; ③ 选取误差值最小的伪标记作为样本的预测标记值. 算法的描述如算法1所示.
算法1. 安全样本标记方法(Safe Labeling method, SL)
输入: 有标记样本集L;
无标记样本x;
有监督分类器
输出: 无标记样本x对应的标记
过程:
For i=1 to m/* m表示数据的分类类别数*/
使用伪标记Mi去标注无标记样本x, 记做yi;
将yi添加到训练集L中;
将L分为k组, 记做L(1), L(2), …, L(k);
For j=1 to k
让L(j)作为测试集, 其它k-1个组中的有标记样本作为训练集;
使用训练集训练分类器Cij;
用Cij去测试测试集;
记录此时的是正确分类率为acci (j);
EndFor
计算第i个伪标记对应的误差: ei=1–(acci(1)+acci(2)+…+acci(k))/k;
EndFor
获取e1, e2, …, em的最小值, 记为emin;
emin对应的标记t作为样本x的预测标记.
该算法保证分类器朝着误差降低的方向进行演化, 能很好的提高标记的正确率, 较好的保证分类器的安全性. 考虑到算法的时间效果, 在G个样本子集中程序并发运行. 最终, 在每个最优特征子集中, 形成G个分类器.
(5)在最优特征子集内进行分类器集成
在最优特征子集内实现G个分类器的集成, 采用最大投票法进行集成, 即将相同标记数目最多的分类器对应的标记作为集成分类器的标记. 集成方法如下:
| $ f(t, b) = \mathop {\arg \max \sum\nolimits_{i = 1}^M {1\{ {y_{ib}} = j\} } }\limits_{1 \le j \le k} $ | (10) |
式中, f(t, b)表示测试样本xt在第b个最优特征子集中的预测标记; yib表示在第b个最优特征子集中, 第i个分类器的预测标记; k表示分类的类别.
(6)在最优特征子集间进行分类器集成
在B个最优特征子集之间也采用最大投票法进行集成, 将集成结果作为输入高维数据的最终分类结果, 扩充高维数据有标记样本的数目. 集成方法如下所示:
| $ f(t) = \mathop {\arg \max \sum\nolimits_{i = 1}^{{B}} {1\{ {{{y}}_i} = j\} } }\limits_{1 \le j \le k} $ | (11) |
式中, f(t)表示测试样本xt的最终标记值, yi表示测试样本xt在第i个最优特征子集中的预测标记, k表示分类的类别.
3 实验及结果分析 3.1 实验平台及数据集在UCI中的高维数据集上进行实验, 实验数据集如表1所示. 实验模拟半监督学习过程, 将样本集分为有标记样本和无标记样本, 其中有标记样本所占的比例很小. 实验中, 与经典半监督集成算法(Co-Forest[9], Tri-training[10], PSEMISEL[15])进行比较, 对提出S3LSE的有效性和鲁棒性进行评估.
3.2 实验评价指标分类问题中, 通常采用下面四个度量来评估结果.
•True Positive (TP): 分类正确, 把原本属于正类的样本分成正类.
•True Negative (TN): 分类正确, 把原本属于负类的样本分成负类.
•False Negative (FN): 分类错误, 把原本属于正类的错分成了负类.
•False Positive (FP): 分类错误, 把原本属于负类的错分成了正类.
| 表 1 实验数据集 |
由于本实验中选取数据集是平衡的, 主要将accuracy等参数作为算法的性能评价指标, 进行30次实验求平均值, 评价本文提出的算法与传统的经典算法之间的差别性, 验证所提出算法的有效性. 基于上述四个度量, 使用式(12)定义Accuracy:
| $ Accuracy = \frac{{TP + TN}}{{TN + FN + TP + FP}} \times 100\% $ | (12) |
实验主要分为以下三大类进行操作:
实验一: 验证提出的半监督算法处理高维数据的有效性. 模拟半监督实验过程, 使用经典半监督集成算法(Co-Forest, Tri-training, PSEMISEL)和本文提出的半监督学习算法S3LSE分别处理高维数据, 对比几种算法的实验结果.
实验二: 验证随机子空间集中特征优化的有效性. 实验分两种进行, 第一种实验不使用特征优化算法, 直接对随机子空间集产生的样本集进行半监督学习, 计算对应高维数据的分类正确率; 第二种实验使用特征优化算法对随机子空间集产生的数据进行优化, 形成最优特征子集, 在最优特征子集中进行半监督学习, 计算对应高维数据的分类正确率. 最后, 对比两种实验的结果.
实验三: 验证本文提出的安全的数据样本标记方法的有效性. 模拟半监督实验, 与其它算法进行比较.
3.3 实验结果及分析 3.3.1 实验一的结果及分析本实验中模拟半监督实验过程, 使用经典半监督集成算法(Co-Forest, Tri-training, PSEMISEL)和本文提出的S3LSE分别处理高维数据, 实验结果如表2所示.
| 表 2 准确率(Accuracy)对比表 |
从表2可以看出, 本文提出的算法S3LSE相对传统的经典半监督集成算法具有较好的分类性能. 这是因为: (1)算法S3LSE充分利用高维数据特征之间的关系, 挖掘高维数据之间的隐含信息, 扩充有标记高维数据的数目, 提高了高维半监督学习的性能. (2)算法S3LSE对新增标记进行可靠性验证的方法, 保证新增标记样本的增加后, 分类器的性能不会恶化, 保证分类器向着误差减小的方向进行演化. (3)算法S3LSE通过多分类器之间的多次集成, 提高分类器的鲁棒性.
3.3.2 实验二的结果及分析第一种实验不使用特征优化算法, 直接对随机子空间集产生的样本集进行半监督学习(算法记作S3LSE - FL), 计算对应高维数据的分类准确率和分类时间; 第二种实验使用特征优化算法对随机子空间集产生的数据进行优化, 形成最优特征子集, 在最优特征子集中进行半监督学习(即S3LSE), 计算对应高维数据的分类准确率和分类时间.
实验结果如表3所示, 从表中可以看出本文提出的算法S3LSE通过对特征集进行优化, 减少了特征的数目, 缩短了分类时间. 和没有使用特征优化的算法S3LSE - FL相比, S3LSE分类准确率并没有因为特征的减少而降低. 同时, 在有些数据集中, S3LSE的分类准确率不但没有降低反而得到了提高, 这是因为特征优化算法选取了最优的特征组合, 删除了一些与分类无关或者作用不大的特征, 新的特征集更有助于分类, 分类性能更好.
3.3.3 实验三的结果及分析实验中模拟半监督学习, 一种方法使用本文提出安全的数据样本标记方法实现对未标记样本进行标记(记做S3LSE, 一种方法使用S3VM[20]实现对未标记样本进行标记(记做S3VM), 对比两种方法的实验性能.
| 表 3 准确率和分类时间对比表: 准确率(%)/分类时间(s) |
实验结果如表4所示, 通过实验结果可以看出, 采用本文提出安全的数据样本标记方法能保证新增加样本标记的可靠性, 分类准确率得到了有效提高. 这是因为本文提出安全的数据样本标记方法保证新样本添加到有标记样本集后, 分类器向着误差降低的方向进行演化.
| 表 4 准确率对比表 |
通过以上实验结果可以看出, 算法S3LSE是一个性能较好的分类算法. 其从探索数据样本空间和特征空间两个角度出发, 结合随机子空间技术和多分类器集成技术, 处理仅包含极少量有标记样本的高维数据分类问题. 它通过对特征子集进行优化, 选取能有效反映特征的相关性、特征之间的冗余度等信息的特征进行半监督学习, 使用安全的数据样本标记算法提高算法安全性, 并使用集成技术提高算法的鲁棒性.
4 结束语本文从探索数据样本空间和特征空间两个角度出发, 提出一种结合随机子空间技术和集成技术的安全半监督学习算法, 处理仅包含极少量有标记样本的高维数据分类问题. 实验结果表明本文的提出的算法能有效发挥集成学习和半监督学习的优势, 同时为处理高维数据开创了一种新途径. 下一步的研究内容是将该算法应用到大规模高维数据分类领域.
| [1] |
梁吉业, 高嘉伟, 常瑜. 半监督学习研究进展. 山西大学学报(自然科学版), 2009, 32(4): 528-534. |
| [2] |
Belkin M, Niyogi P. Semi-supervised learning on Riemannian manifolds. Machine Learning, 2004, 56(1–3): 209-239. |
| [3] |
Wang M, Fu WJ, Hao SJ, et al. Scalable semi-supervised learning by efficient anchor graph regularization. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(7): 1864-1877. DOI:10.1109/TKDE.2016.2535367 |
| [4] |
Sheikhpour R, Sarram MA, Gharaghani S, et al. A survey on semi-supervised feature selection methods. Pattern Recognition, 2017, 64: 141-158. DOI:10.1016/j.patcog.2016.11.003 |
| [5] |
刘建伟, 刘媛, 罗雄麟. 半监督学习方法. 计算机学报, 2015, 38(8): 1592-1617. |
| [6] |
周志华. 基于分歧的半监督学习. 自动化学报, 2013, 39(11): 1871-1878. |
| [7] |
Yu ZW, Zhang YD, Chen CLP, et al. Multiobjective semisupervised classifier ensemble. IEEE Transactions on Cybernetics, 2018.
|
| [8] |
Roy M, Ghosh S, Ghosh A. A novel approach for change detection of remotely sensed images using semi-supervised multiple classifier system. Information Sciences, 2014, 269: 35-47. DOI:10.1016/j.ins.2014.01.037 |
| [9] |
蔡毅, 朱秀芳, 孙章丽, 等. 半监督集成学习综述. 计算机科学, 2017, 44(S1): 7-13. |
| [10] |
Zhou ZH, Li M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(11): 1529-1541. DOI:10.1109/TKDE.2005.186 |
| [11] |
Mallapragada PK, Jin R, Jain AK, et al. SemiBoost: Boosting for semi-supervised learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(11): 2000-2014. DOI:10.1109/TPAMI.2008.235 |
| [12] |
Yaslan Y, Cataltepe Z. Co-training with relevant random subspaces. Neurocomputing, 2010, 73(10–12): 1652-1661. |
| [13] |
Yan Y, Xu ZW, Tsang IW, et al. Robust semi-supervised learning through label aggregation. Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix, AZ, USA. 2016. 2244–2250.
|
| [14] |
Stanescu A, Caragea D. An empirical study of ensemble-based semi-supervised learning approaches for imbalanced splice site datasets. BMC Systems Biology, 2015, 9(S5): S1. |
| [15] |
Yu ZW, Lu Y, Zhang J, et al. Progressive semisupervised learning of multiple classifiers. IEEE Transactions on Cybernetics, 2018, 48(2): 689-702. DOI:10.1109/TCYB.2017.2651114 |
| [16] |
Ding SF, Jia HJ, Du MJ, et al. A semi-supervised approximate spectral clustering algorithm based on HMRF model. Information Sciences, 2017, 429: 215-228. |
| [17] |
Liu L, Yang LC, Zhu B. Sparse feature space representation: A unified framework for semi-supervised and domain adaptation learning. Knowledge-Based Systems, 2018, 156: 43-61. DOI:10.1016/j.knosys.2018.05.011 |
| [18] |
Yu ZW, Luo PN, You J, et al. Incremental semi-supervised clustering ensemble for high dimensional data clustering. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(3): 701-714. DOI:10.1109/TKDE.2015.2499200 |
| [19] |
赵建华. 一种基于交叉验证思想的半监督分类方法. 西南科技大学学报, 2014, 29(1): 34-38, 48. DOI:10.3969/j.issn.1671-8755.2014.01.008 |
| [20] |
蒋长鸿, 范钢龙. 先验信息优化的S3VM算法模型研究. 西北工业大学学报, 2017, 35(5): 786-792. DOI:10.3969/j.issn.1000-2758.2017.05.007 |
 2019, Vol. 28
2019, Vol. 28



