分形艺术审美的产生及特殊的生成规则, 打破了常规审美的标准. 利用分形理论可以生成超出人类想象力的图案, 并应用于织物花型设计, 这是计算机技术在艺术设计中的典型应用^[1,2]. 随着计算机技术的进步, 分形理论在数字艺术图形设计、装饰、纺织领域得到了广泛应用^[3,4]. 但是根据分形理论生成的图形, 一般都是单个的花型, 不具周期反复的规律. 而在织物面料、包装纸等实际产品的花型设计中, 往往需要连续纹样的图形, 需要将单个图形转化为连续纹样图^[5]. 代沛涵在《分形在纺织纹样设计上的应用》一文中介绍了四方连续纹样作为一种节奏均匀、韵律统一、整体感强的图形组织方式, 可以将分形图形作为纹样单元进行设计^[6,7]. 目前业界还没有自动实现单个图形转换为连续纹样图形的算法和软件, 人工转换需要设计者手动对图形单元进行分割、再布布局之后, 将图形进行重复排列, 费时费力且效率低下, 这成为了限制计算机自动生成花型在实际应用中的“最后一公里”问题^[8]. 本文提出了一种将单个花型自动转为四方连续纹样的方法. 在分析花型内容特征的基础上, 提供多种四方连续拼接方式, 供设计师参考. 本方法计算复杂度低, 适用范围广, 具有良好的实际应用价值.

1 算法原理

本文提出的方法先将分形图形缩放到统一的分辨率区间, 然后利用Canny计算检测边缘特征, 判断花型分布及边缘特征一致性, 并用矩形窗口轮寻机制提取主花型; 接着通过灰度共生矩阵提取分形图的纹理特征, 选择最佳的拼接方法; 最后利用选择的方法对主花型进行拼接, 生成四方连续纹样. 流程如图1.

1.1 边缘检测确定花型区域

边缘检测处理后的图片包含了分形图中花型的相对位置与花型的边缘特征. 本文采用自适应阈值的Canny边缘检测^[9]. 与LOG算子相比, Canny算子计算图像一阶差分, 具有速度快、边缘信息定位准确的优点, 与Sobel、Prewitt等一阶微分算子相比, Canny算子边缘定位准确且噪声抑制效果好. 图3为图2对应示例花型在OTSU最大类间差^[10]确定分割阈值后得到的边缘检测结果.

1.2 花型提取处理

根据上述边缘检测结果显示, 图2中示例2的分形花型像素点集中, 四周模糊, 四周像素灰度值较低, 采用矩形轮寻机制对其进行目标区域(主花形区域)提取. 矩形轮寻机制是用矩形框按设定步长去遍历整张图片, 选取全局图片部分视野, 再对矩形框内像素点进行操作, 具体操作流程如下:

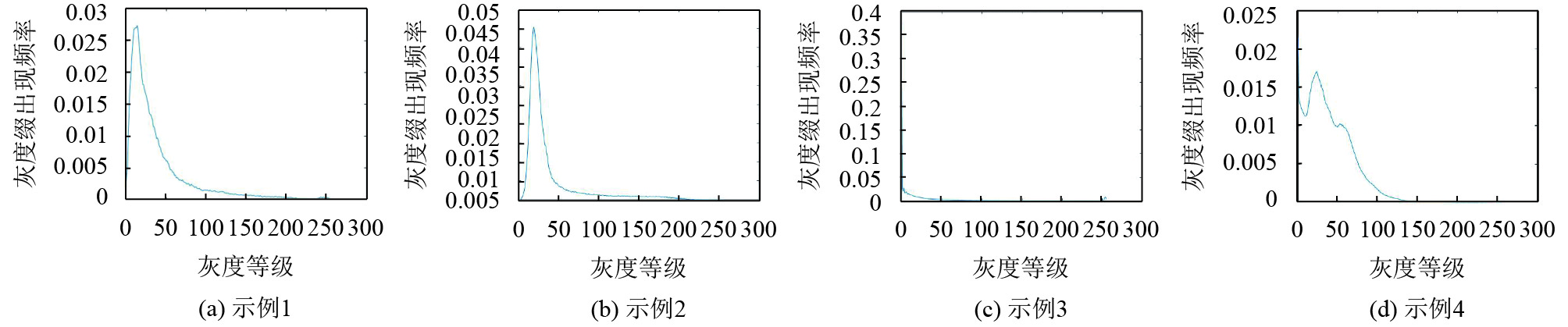
1)自定义一个矩形大小, 本文设置初始默认长宽各为原图片的1/4大小. 图4为图2中对应示例的灰度等级出现概率直方图.

2)利用灰度概率对分形图Otsu二值化处理^[10], 统计矩形内的像素点个数. 如果矩形内非零像素点占比达到1/5, 说明矩形大小合适, 记录包含边缘像素的矩形起始点坐标. 若占比小于1/5, 则说明矩形较大, 矩形长宽依次减小, 若矩形长宽减小到图片的1/10后非零像素占比仍小于1/5, 则判定为花型区域过小, 不适合进行提取. 在进行矩形窗口循环计算过程中, 考虑到算法的运行效率, 需要控制矩形框的大小, 矩形越小, 计算图像信息占比越准确, 但随着矩形框数量增加, 计算量也增加, 有可能导致运行效率低的问题, 矩形轮寻机制中矩形数量控制在2000以下, 计算一张分形图大约需要0.8–1.5秒, 可满足实际应用需求.

3)为精确定位包含主要花型的外接矩形, 得到包含所有边缘像素点矩形的起始坐标,再求包含所有起始点的最小外接矩形, 并将此矩形设定为目标区域, 图5分别用红色框标注了图2中对应示例所求得的最小外接矩形, 并将该部分设置为感兴趣(ROI)区域.

4)将感兴趣(ROI)区域提取并作为基础纹样进行直接拼接或错位拼接.

1.3 灰度共生矩阵提取纹理特征

根据1.2节提取的基础纹样中花型形态差异, 纹样四边纹理特征决定了基础纹样是否适合拼接. 纹理特征是灰度在空间分布上的相关性, 灰度共生矩阵是涉及像素距离和角度的矩阵函数, 它通过计算图像中一定距离和一定方向的两点灰度之间的相关性, 反映图像在方向、间隔、变化幅度及快慢上的综合信息^[11–13]. 本文灰度共生矩阵方向设定了0度、45度、90度、135度4个方向, 设定为16个灰度级,提取常用的5个特征性: 能量(角二阶矩), 熵, 对比度, 逆差距, 相关性. 结合灰度特征需求, 提出了适应于分形图集的四边灰度分布均匀度量公式H. 相关公式如下:

$Asm = \sum\limits_i {\sum\limits_j {P{{(i,j)}^2}} } $

(1)

$Ent = \sum\limits_i {\sum\limits_j {P(i,j){{\log }_2}P(i,j)} } $

(2)

$H = {w_1}Asm + {w_2}Ent,Asm > 0.2,Ent < 4$

(3)

上述公式中 $P(i,j)$ 表示四个方向上的不同灰度共生矩阵元素, $Asm$ (能量)是图像纹理的灰度变化稳定程度的度量, 值越大说明灰度均匀且纹理规则, $Asm$ 值与灰度均匀成正相关关系, 所以 ${w_1}$ 取正. $Ent$ (熵)是对灰度分布复杂度的度量, 其值越小, 纹理复杂度越低, $Ent$ 值与纹理复杂度成负相关, 所以 ${w_2}$ 取负. 公式(3)是综合了两种灰度分布特征, 用来筛四边选灰度均匀且复杂度低的分形图形, 所求得 $H > 1$ 时认为符合条件. 经过实验分类, 公式中 ${w_1} = 5$ , ${w_2} = - 0.25$ . 纹理特征提取具体判定方法如下:

1)对分形图边缘进行四边像素提取, 分别提取四边(20像素单位), 并转换为灰度图像.

2) 通过灰度共生矩阵提取纹理特征, 通过相关性筛选纹理灰度相似程度, 计算H判断分形图的灰度纹理均匀程度(特征值为4个方向共生矩阵的平均值).

1.4 四方连续拼接

四方连续纹样的组织方式主要有散点式、连缀式、重叠式三种. 本文算法主要对分形图进行花纹提取, 用于散点式纹样组织方式. 其中散点式组织方式可分为平排或错接. 文中将平排定义为直接拼接, 错接定义为错位拼接. 直接拼接要求基础纹样进行水平垂直平移或镜面翻转. 错位拼接要求根据自定义参数(如1/2、1/3、2/5等)错位拼接.

针对错位拼接因为偏移导致的边缘花型衔接性差的问题. 本文采取对错位拼接部分(注: 取拼接点左右(上下)各1个像素的长宽, 拼接部分像素总数 $ S = 3\times$ $Dstrows$ 或 $S = 3 \times Dstcols$ , $Dstrows$ 与 $Dstcols$ 分别为基础纹样的宽长), 进行二次低阈值的边缘检测, 统计拼接处的边缘像素, 若拼接边缘像素少于15, 则证明错位拼接效果良好, 图6中示例1的拼接处仅有6个边缘像素, 适合错位拼接, 示例2的拼接处包含过多边缘像素, 不适合错位拼接.

2 实验结果展示

根据分形图分类中对分形图是否需要提取花型, 基础纹样按直接拼接或错位拼接, 生成如表2所示几种四方连续纹样.

3 结语

本文设计了一种针对分形图中花型内容的四方连续纹样自动生成算法, 结合边缘检测统计判定边缘特征, 再用矩形轮寻机制提取制作基础纹样, 提取分析分形图纹理特征, 最后通过直接拼接与错位拼接两种拼接方式, 快速生成四方连续纹样并显示. 实验结果表明, 相较于借助软件工具进行设计, 该方法生成纹样效果美观, 计算复杂度低, 通用性强.