云计算服务的广泛应用极大地促进了数据中心的发展, 但与此同时, 规模日趋庞大的数据中心产生了巨大的能耗. 根据美国劳伦斯伯克利国家实验室最近发布的美国数据中心能源使用报告, 在2014年, 美国的数据中心能耗已达到700亿千瓦时, 约占美国总用电量的1.8%[1]. 数据中心的能耗问题引起了IT界的密切关注, 能耗管理也成为了近年来的研究热点. 数据中心能耗优化的相关研究往往需要大量的实验, 而在实体服务器集群环境中, 实验参数出现差错或中间结果失效都会导致实验的失败, 重启服务会大大增加实验周期, 并且在实体集群中进行实验需要承担巨额的费用[2]. 云计算仿真平台很好的解决了这一问题, 使面向大规模云资源能耗优化的相关研究能够更加经济、高效. 但仿真技术也存在着一定的局限性, 仿真平台无法直接测量能耗, 只能通过内置的能耗模型进行估算. 因此, 能耗评估是云计算仿真的关键环节, 直接决定了仿真实验的准确度和可信度.
1 云计算数据中心能耗评估方法概述目前已有的云计算数据中心的能耗评估方法可以大致分为两类, 一是云计算仿真平台中内置的能耗模型, 二是面向真实的物理集群进行的能耗评估.
当前应用最为广泛的云计算仿真平台是澳大利亚墨尔本大学的网格实验室开发的CloudSim[3], 为估算仿真平台的能耗, CloudSim内置了Power模块, 提供了依赖于服务器CPU利用率的能耗评估模型. CloudSim的能耗模型可以分为两类, 一类分别采用CPU利用率的平方根、线性、平方、立方来计算能耗, 另一类依据SPECpower记录的服务器功耗情况对特定的7种服务器进行能耗计算. 其中SPECpower能耗模型采用了服务器真实的CPU使用率和能耗数据作为样本, 选取了11个采样数据点, 最终采用一元分段式模型来进行能耗计算.
除了仿真平台的内置能耗模型之外, 很多学者进行了面向真实集群的能耗评估方法相关研究. 文献[4]的研究表明, 数据中心服务器的能耗可以利用CPU利用率来计算, 可以简单高效地采用一元线性回归数学模型来进行能耗建模. 而文献[5]认为服务器的能耗和CPU的利用率不是完全的线性关系, 服务器的能耗增速随着CPU利用率的增加逐渐增大, 之后增速逐渐平稳再迅速减小, 直到能耗值达到最大. 文献[6]指出, 数据中心的能耗与CPU利用率、内存、主板、外存等有关, 仅仅使用CPU利用率来进行能耗估算可能会导致能耗估算误差较大. 文献[7]提出了利用CPU实时利用率、CPU实时频率和内存利用率, 结合多元线性回归进行能耗建模, 提高了能耗建模的精确度, 但采用的参数较多. 在文献[8]中, 采用基于CPU和内存使用率的多元线性和多元非线性方法进行能耗建模, 选用的参数较少, 且结果较为准确, 适合移植到仿真环境中, 但在建模过程中没有考虑CPU利用率对内存能耗的影响, 以及在计算节点启动过程中的状态转换能耗. 随着服务器处理器的不断改进, 相关学者开始从性能计数器的角度进行能耗建模的研究. 在文献[9]中, 采用性能事件进行建模, 定义了22个性能事件, 通过全回归的数学模型进行能耗评估. 在文献[10]中, 选用CPU、内存、I/O等主要组件的细粒度性能计数器作为特征值集合, 并建立该集合与运行时系统总功耗的对应关系, 通过多元线性回归的方法确定相关系数, 最终得到较为精确的能耗模型. 基于性能计数器的能耗建模方法具有较高的准确性, 但测算数据中心能耗的监控参数过多,难以在仿真平台中实现.
针对以上问题, 本文对CloudSim云计算仿真平台的能耗模块进行了修改, 提出了适用于仿真环境能耗评估方法, 该方法基于计算节点的CPU和内存利用率, 并考虑了状态转换能耗和CPU 利用率对内存能耗的影响, 利用多元回归进行建模. 本文通过实验对比了CloudSim一元线性模型、CloudSim一元分段式模型、多元线性模型、多元非线性模型的能耗评估效果, 验证了本文提出的能耗评估方法的有效性.
2 仿真环境下的数据中心能耗评估原理云计算仿真平台的主要功能是为数据中心资源调度等相关实验提供实验环境, 尽管仿真环境在规模和精度等方面与真实集群有一定的差距, 但它可以创建一个近似的模拟环境, 使数据中心资源调度相关实验可以在一个较小的计算环境中进行. 应用于仿真环境中的能耗评估方法, 应该在保证易于建模的基础上, 尽量提高其评估的准确性, 因此需要监测多的性能参数或者过于复杂的决策评估过程并不适用于仿真环境.
云计算数据中心的总能耗包括云计算中心的计算节点能耗、网络设备能耗、存储设备能耗、温控设备能耗和其他设备能耗. 网络、存储、温控及其他设备能耗的变化相对较小, 因此在仿真环境的能耗评估过程中, 我们将其视为恒定的能耗. 数据中心的计算节点可能是同构的也可能是异构的, 为简化能耗评估过程, 我们假定数据中心中所有的计算节点都是同构的, 并且具有相同的配置, 那么数据中心的能耗可以表示为:
| $E(DC) = \sum\limits_{i = 1}^N {E(i)} \;\;{\rm{ + }}E(other)$ | (1) |
其中, E(DC)为数据中心的总能耗, N代表同构计算节点个数, E(i)代表同构节点能耗, E(other)代表网络、存储、温控和其他设备的恒定能耗.
计算机系统的能耗通过功率来计算, 在实际情况下, 计算节点能耗并不能以一个固定的功率和时间做简单乘积来度量, 对于单个计算节点来说, 能耗与功率的关系如式(2)所示:
| ${E_i} = {\int_0^T P _{run}}\left( t \right)dt + s \cdot {E_s}$ | (2) |
其中, E(i)为云计算数据中心同构节点能耗, Prun为同构节点的运行功率, s为节点i发生状态转换的次数, Es为节点i启动时的瞬时能耗. 服务器在启动时功率会迅速上升, 产生较大的能耗, 忽略启动瞬时能耗会影响数据中心能耗模型的准确度. 特别是对于虚拟机分配和迁移算法的能耗评估, 如果不考虑启动能耗, 将无法衡量物理机频繁的开闭产生的能耗. 启动能耗可以通过测量得到, 这里用常量表示. 通过上述分析,将云计算数据中心的能耗评估简化为同构计算节点实时功率建模.
在实际情况下, 计算机功率的变化情况是十分复杂的, 受多种因素的综合影响. 其中CPU是计算机的主要能耗组件, 已有的基于计算机系统的资源利用率的能耗模型几乎都首先将CPU的能耗考虑在内. 内存组件本身能耗消费不高, 但CPU与内存互相关联, 任务的运行往往伴随着CPU和内存利用率的同时提高, 从而导致整体能耗的提高, 因此内存也是能耗评估时需考虑在内的重要组件[8]. 另外硬盘、网络接口等组件也会产生一定的能耗, 但对整体能耗的影响相对较小, 为简化能耗模型, 可以将计算节点的实时功率按各个组件进行分解, 表示为:
| $P(total) = P(cpu) + P(mem) + P(others)\;\;\;\;$ | (3) |
其中, P(cpu)和P(mem)分别表示计算机处理器和内存对功率的影响, P(others)表示硬盘、网络接口等其他组件对计算节点功率的影响. 由于硬盘和网络接口对整体能耗影响较低, 且对于仿真环境来说引入过多变量将导致模型过于复杂, 大大增加重写能耗模型的难度, 因此我们只针对与能耗关系最紧密的处理器和内存进行建模, 网络接口和硬盘的能耗将被视为常量. 其中处理器能耗用CPU利用率来构建, 内存能耗通过内存利用率来构建.
3 仿真环境下的云计算数据中心能耗评估方法 3.1 数据准备为保证仿真环境下的数据中心能耗模型的可信度和准确度, 在建模之前需要收集大量的真实数据, 根据上一节阐述的能耗建模原理, 采样数据应包括同构节点对应的CPU利用率、内存利用率和实时功率.
在本文中, 同构节点的操作系统为CentOS, 在Linux系统中, 可以采用top命令来监测系统的CPU利用率和内存利用率. 执行top命令会显示CPU和内存的相关信息, 可以表示为:
Cpu(s): 3.3 us, 1.4 sy, 0.0 ni, 94.7 id, 0.6 wa, 0.0 hi, 0.0 si, 0.0 st
Mem: 3803368 total, 2117404 free,1084500 used, 601464 buffers
其中与CPU利用率相关的参数有us、sy和id, 分别代表用户空间占用CPU的百分比、内核空间占用CPU的百分比和空闲百分比, CPU利用率的计算公式可以表示为
| $U(cpu) = U(us) + U(sy) = 1 - U(id)\;\;\;\;$ | (4) |
与内存相关的参数有total, used,free, buffers, 分别表示物理内存总量、使用中的内存、空闲内存和缓存内存, 内存利用率的计算公式可以表示为:
| $\;U(mem) = \frac{{total - free - buffers}}{{total}} = \frac{{used}}{{total}}$ | (5) |
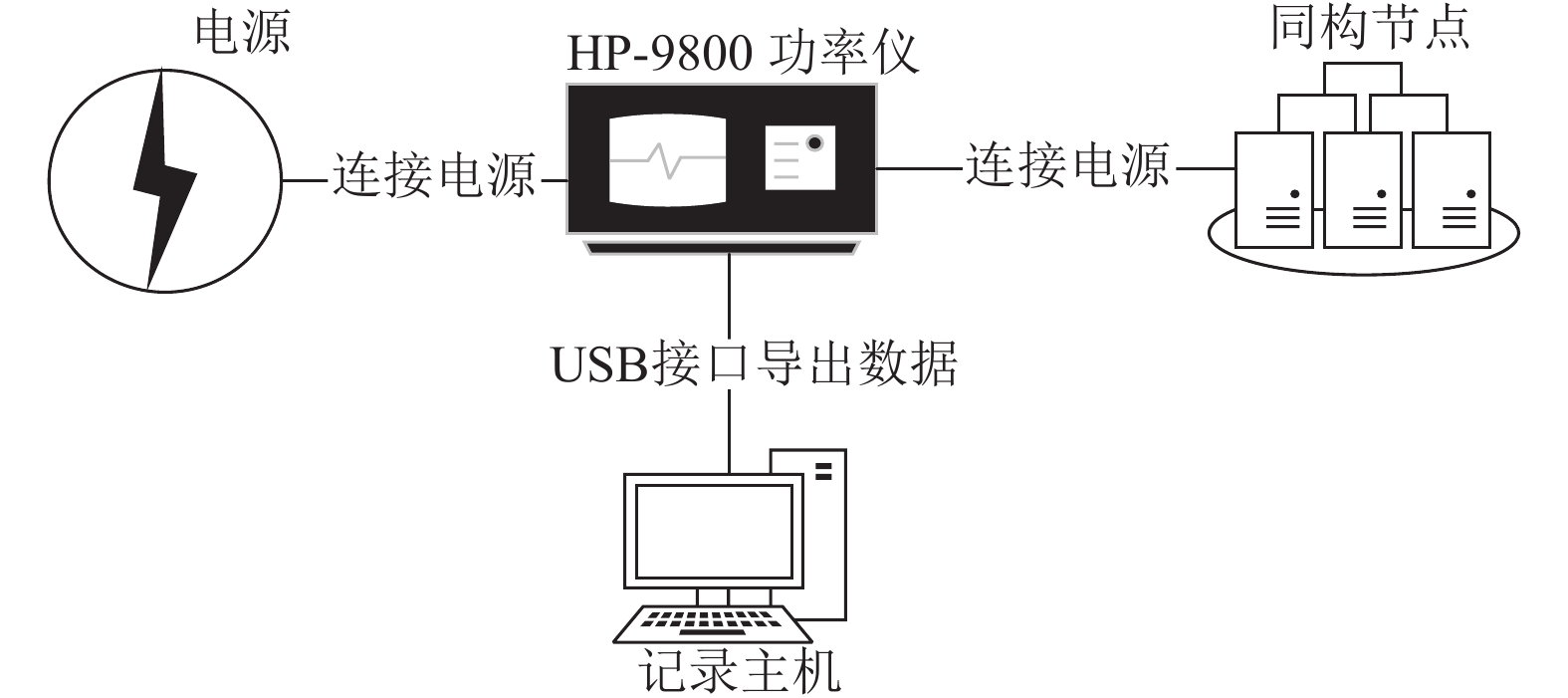
同构节点的实时功率采用HP-9800功率仪进行测量, HP-9800功率仪包含USB接口, 可以连接收集数据的主机, 通过代理软件将功率和对应的时间导入到计算机中. 同构节点实时功率采样拓扑如图1.
|
图 1 实时功率采样拓扑 |
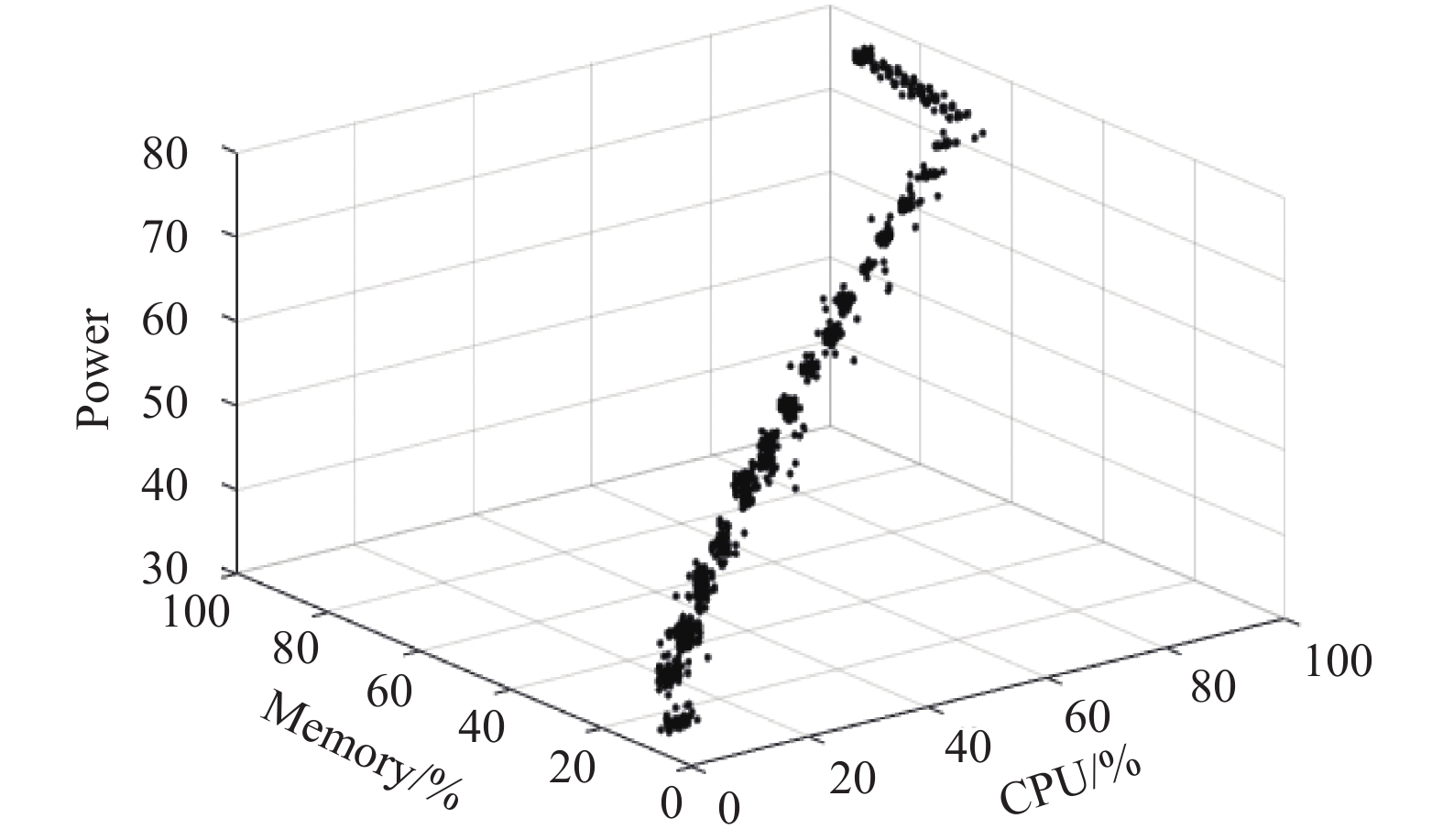
在完成CPU利用率、内存利用率和实时功率的数据采集后, 通过采集时间进行匹配, 形成功率、CPU利用率、内存利用率的三元组, 采样结果如图2.
|
图 2 采样结果图 |
3.2 能耗模型
在本文中, 通过采样得到了近3800组CPU利用率、内存利用率和实时功率数据, 将CPU利用率和内存利用率作为自变量, 实时功率作为因变量, 通过多元线性回归和多元非线性回归的方式进行能耗建模与验证.
3.2.1 多元线性回归模型多元线性回归是处理变量间相关关系时常用的分析手段, 含n个变量的多元线性回归模型可以表示为:
| ${\rm{y = }}{\beta _{\rm{0}}}{\rm{ + }}{\beta _{\rm{1}}}{{\rm{x}}_{\rm{1}}}{\rm{ + }}{\beta _{\rm{2}}}{{\rm{x}}_{\rm{2}}}{\rm{ + }}\cdots + {\beta _n}{{\rm{x}}_n} + \varepsilon \;\;\;\;$ | (6) |
其中, β0, β1, β2, …, βn为回归系数, ε为随机误差, 多元线性回归的过程就是对回归系数和误差的计算. 利用多元线性回归方法进行建模, 因变量与每个自变量需大致满足线性关系, 即要求自变量CPU利用率、内存利用率与因变量实时功率的线性相关系数大于0.75, 线性相关系数计算公式为:
| $\;\;r = \frac{{\displaystyle\sum\limits_{i = 1}^n {({x_i} - \bar x)} ({y_i} - \bar y)}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} \sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} } }}$ | (7) |
将采样的得到的3800组数据代入上式进行计算, CPU利用率、内存利用率与功率的线性相关系数分别为: rcpu=0.9603, rmem=0.9537. 由此可以得出, CPU利用率、内存利用率与功率之间的线性关系较强, 可以尝试采用多元线性回归的方式进行能耗建模. 多元线性回归的能耗模型可以表示为:
| $P{\rm{ = }}{\beta _{\rm{0}}}{\rm{ + }}{\beta _{\rm{1}}}{{{U}}_{{{cpu}}}}{\rm{ + }}{\beta _{\rm{2}}}{U_{{{mem}}}}\;\;\;\;$ | (8) |
其中, β0, β1, β2为需要确定的回归系数, 通过回归分析可以得到β0的值为36.6309, β1的值为0.5315, β2的值为−0.1644.
3.2.2 多元非线性回归模型多元线性回归模型简单、高效并且易于使用, 但它更适用于自变量之间相互独立的问题. 而在本文中, 由于CPU和内存是通过主板连接的一个整体, CPU和内存的能耗产生可能会相互影响, 并且功率和CPU利用率、内存利用率不是绝对的线性关系, 为进一步提高能耗模型的准确性, 本文引入了非线性模型, 并将CPU对内存的影响考虑在内.
首先采用多项式模型为基本函数, 初步得到非线性能耗模型, 计算公式如下:
| $P{\rm{ = }}{\beta _{\rm{0}}}{\rm{ + }}{\beta _{\rm{1}}}{{{U}}_{{{cpu}}}}{\rm{ + }}{\beta _{\rm{2}}}{{U}}_{{{cpu}}}^{\rm{2}}{\rm{ + }}{\beta _{\rm{3}}}{U_{{{mem}}}}{\rm{ + }}{\beta _{\rm{4}}}U_{{{mem}}}^{\rm{2}}\;\;\;\;$ | (9) |
CPU是计算机的主要能耗组件, 并且对内存能耗存在着一定的影响, 因此内存相关系数β3, β4可能与CPU利用率相关. 我们首先通过多项式回归分析, 得到只考虑CPU利用率时β0, β1, β2的值. 之后将采样数据分为38组, 每组一百份数据, 在β0, β1, β2值固定的情况下, 观察CPU利用率的变化对内存的相关系数β3, β4的影响. 分析发现, β4的值随CPU利用率变化不明显, 在一定的区间内上下浮动, 而β3随CPU利用率变化明显, 其变化趋势如图3.

|
图 3 CPU利用率与内存相关系数分布图 |
通过曲线拟合得到CPU利用率和内存的相关系数β3函数形式, 之后结合式(9)得到非线性能耗评估模型, 如式(10)所示:
| $\left\{ \begin{gathered} P{\rm{ = }}{\beta _{\rm{0}}}{\rm{ + }}{\beta _1}{U_{cpu}}{\rm{ + }}{\beta _{\rm{2}}}U_{cpu}^{\rm{2}}{\rm{ + }}\operatorname{f} {\rm{(}}{{{U}}_{cpu}}{\rm{)}}{U_{mem}}{\rm{ + }}{\beta _4}U_{mem}^{\rm{2}} \hfill \\ \operatorname{f} {\rm{(}}{{{U}}_{cpu}}{\rm{)}} = {\gamma _0} + {\gamma _1}{U_{cpu}} + {\gamma _2}{\rm{ln(}}{{{U}}_{cpu}}{\rm{)}} \hfill \\ \end{gathered} \right.$ | (10) |
得到函数基本模型后, 通过进一步非线性回归分析, 确定各个系数值, 其中β0, β1, β2, β4分别取值为20.5604, 1.3027, –0.0107, –0.0041, γ0, γ1, γ2分别取值为1.5963, 0.0200, –0.6236.
3.3 预测和评估完成能耗模型建立后, 将依据能耗模型进行能耗评估, 为比较评估结果的精确度, 将采用相对偏差和平均相对偏差作为评估标准. 其中相对偏差反应每个采样点的评估精度, 平均相对偏差反应模型评估的整体情况. 相对偏差和平均相对偏差的计算公式如下:
| ${P_{\text{相对偏差}}}{\rm{ = }}\frac{{{P_{\text{预测}}}{\rm{ - }}{P_{\text{真实}}}}}{{{P_{\text{真实}}}}}$ | (11) |
| ${P_{\text{平均相对偏差}}}{\rm{ = }}\frac{{\displaystyle\sum\limits_{{\rm{i = 1}}}^{\rm{n}} {\left| {{P_{\text{偏差}}}} \right|} }}{n}$ | (12) |
为验证本文提出的能耗模型的有效性, 本文采用CloudSim内置模型作为参考组设计了对比实验. CloudSim中内置的能耗模型全部为基于CPU利用率的一元模型, 在对比实验中选择最为常用的一元线性模型和较为准确的一元分段式模型作为对照组. 其中一元分段式模型将CPU利用率以10%为梯度进行分段, 设置11个分段点, 在每个分段内采用一元线性模型来计算服务器功率, 实验的软硬件环境见表1.
| 表 1 实验软硬件参数表 |
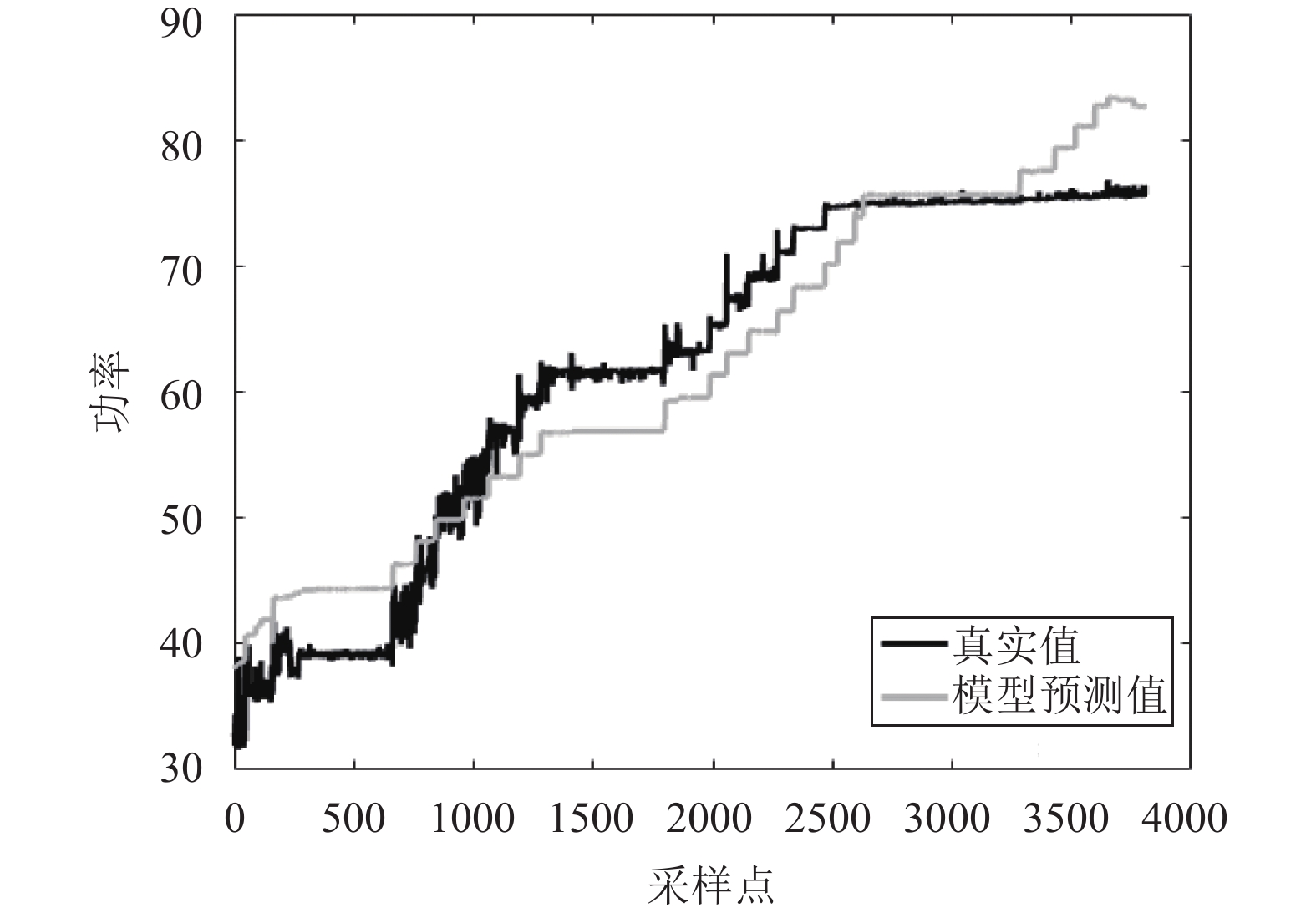
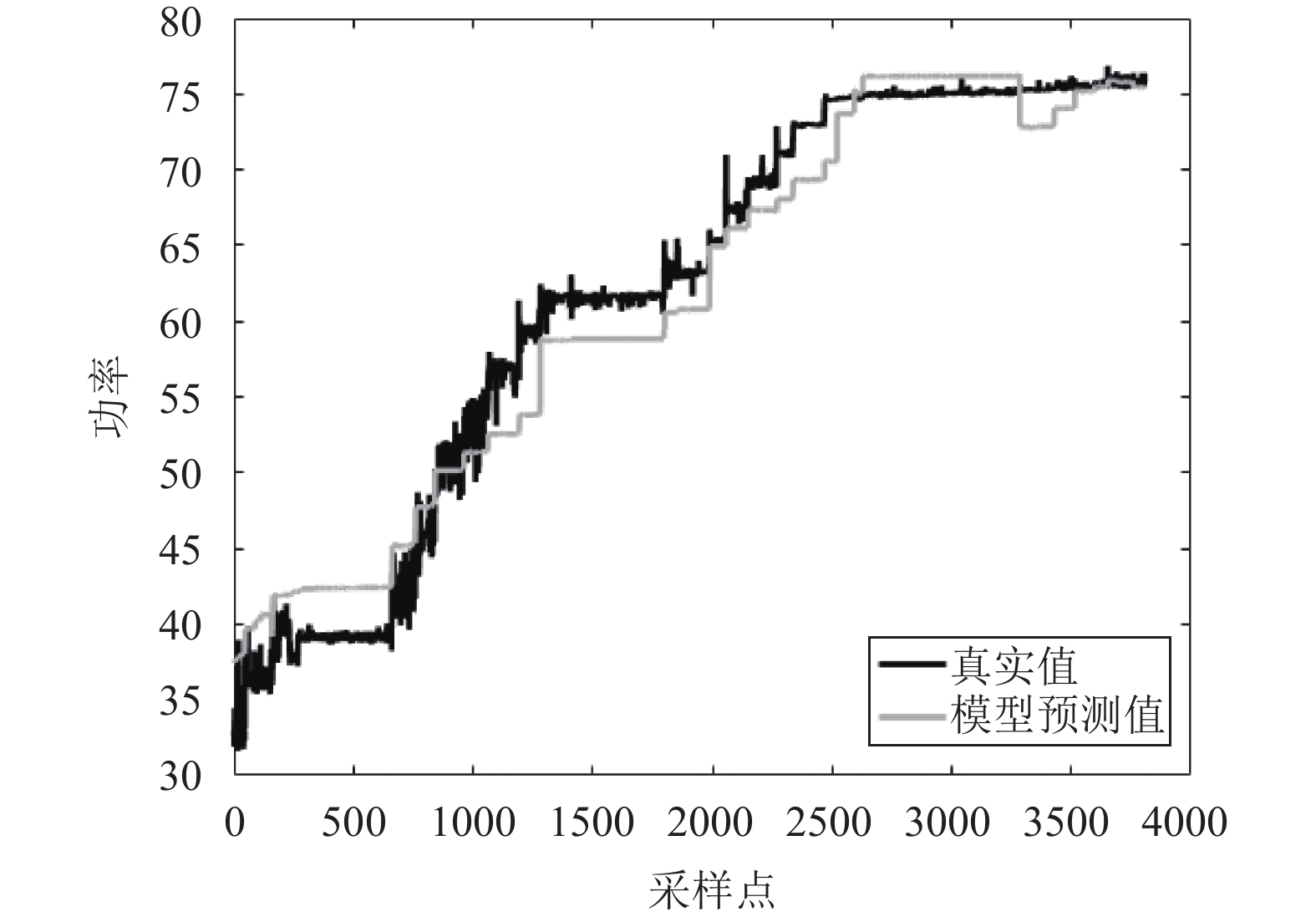
CloudSim一元线性模型、CloudSim一元分段式模型、多元线性模型、多元非线性模型的能耗预测值和能耗真实值的对比情况依次如图4至图7所示.
通过对比各个能耗模型的预测值和能耗真实值可以直观地判断各个模型的预测准确性. 之后, 根据公式(11)计算可以得到CloudSim仿真平台一元线性模型、CloudSim一元分段式模型、多元线性模型、多元非线性模型的相对偏差, 反应了各个模型每个采样点的预测误差分布情况. 以上四个模型的相对偏差情况如图8至图11所示.
|
图 4 CloudSim一元线性模型预测情况 |
|
图 5 CloudSim一元分段式模型预测情况 |

|
图 6 多元线性回归模型预测情况 |
根据式(12)计算可得到各个模型的平均相对偏差, 其中CloudSim一元线性模型的平均相对偏差为0.0659, CloudSim一元分段式模型为0.0421, 多元线性模型的平均相对偏差为0.0261, 多元非线性模型为0.0094, 通过对比以上四种模型的预测情况、相对偏差和平均相对偏差, 可以发现, 多元线性模型、多元非线性模型预测效果均优于CloudSim平台中的内置模型, 其中考虑了CPU对内存能耗影响的多元非线性模型有较为明显的优势. 因此, 选择本文提出的多元非线性模型重写仿真平台的能耗评估方法, 用于资源调度相关实验的能耗评估.

|
图 7 多元非线性回归模型预测情况 |

|
图 8 CloudSim一元线性模型相对偏差 |
5 结论与展望
本文针对云计算仿真平台中数据中心能耗评估误差较大的问题, 提出了基于计算机CPU和内存利用率的多元非线性能耗评估方法. 实验结果表明, 本文提出的多元非线性能耗模型在适用于云计算仿真平台的同时, 有较高的准确性, 有效的提高了仿真环境中的能耗评估效果. 在本文中为简化能耗评估过程, 将数据中心的网络、存储等设备产生的能耗和计算节点的硬盘、网络接等口产生的能耗都视为了常量, 接下来的研究将分析这些设备或组件的能耗特性, 在尽量保证仿真过程简单可行的前提下, 进一步提高仿真模型的精确度. 此外, 还将在重写了能耗模型的CloudSim仿真平台中实现资源调度算法, 以本文的能耗评估方法为标准进行能耗感知相关实验.

|
图 9 CloudSim一元线分段模型相对偏差 |

|
图 10 多元线性回归模型相对偏差 |

|
图 11 多元非线性回归模型相对偏差 |
| [1] |
Shehabi A, Smith S, Sartor D, et al. United States Data Center energy usage report. Berkeley: Lawrence Berkeley National Laboratory, 2016.
|
| [2] |
林伟伟, 吴文泰. 面向云计算环境的能耗测量和管理方法. 软件学报, 2016, 27(4): 1026-1041. |
| [3] |
Calheiros RN, Ranjan R, De Rose CAF, et al. CloudSim: A novel framework for modeling and simulation of cloud computing infrastructures and services. arXiv: 0903.2525, 2009.
|
| [4] |
Chen G, He WB, Liu J, et al. Energy-aware server provisioning and load dispatching for connection-intensive internet services. Proceedings of the 5th USENIX Symposium on Networked Systems Design and Implementation. San Francisco, CA, USA. 2008. 337–350.
|
| [5] |
Fan XB, Weber WD, Barroso LA. Power provisioning for a warehouse-sized computer. ACM Sigarch Computer Architecture News, 2007, 35(2): 13-23. DOI:10.1145/1273440 |
| [6] |
Basmadjian R, Ali N, Niedermeier F, et al. A methodology to predict the power consumption of servers in data centres. Proceedings of the 2nd International Conference on Energy-Efficient Computing and Networking. New York, NY, USA. 2011. 1–10.
|
| [7] |
陈俊, 胡悦, 杨娇, 等. 云计算数据中心实时能耗建模. 计算机工程与设计, 2017, 38(9): 2494-2497, 2555. |
| [8] |
罗亮, 吴文峻, 张飞. 面向云计算数据中心的能耗建模方法. 软件学报, 2014, 25(7): 1371-1387. |
| [9] |
Isci C, Martonosi M. Runtime power monitoring in high-end processors: Methodology and empirical data. Proceedings of the 36th Annual IEEE/ACM International Symposium on Microarchitecture. San Diego, CA, USA. 2003. 93–104.
|
| [10] |
程华, 陈左宁, 孙凝晖, 等. 一种基于细粒度性能计数器建立系统实时功耗模型的方法. 计算机学报, 2014, 37(3): 687-699. |
 2019, Vol. 28
2019, Vol. 28



