由于汽车刹车片生产工序相对其它复杂产品工序较少, 因而以往刹车片生产计划的排产主要依靠人工来完成. 但是随着刹车片市场对刹车片品种的多样化和个性化需求不断增加, 使得刹车片的种类日益增多, 从而逐渐形成一种多品种变批次的生产模式[1–3]. 这使得之前依靠人工进行刹车片生产计划排产的模式不能高效适用于新的生产模式, 且生成的排产计划难以合理分配生产资源, 给企业带来不必要的生产资源浪费.
多品种变批次生产模式的排产问题属于NP-hard问题[4–6], 其中NP是指非确定性多项式, 这类问题无法通过公式推导来精确求解, 只能通过“猜测”来间接地获取结果, 因此仅通过人工来解决该问题, 很难求得最优解. 另外目前针对刹车片生产计划的排产问题的研究很少, 因此, 有必要对刹车片生产计划的排产问题进行深入的研究.
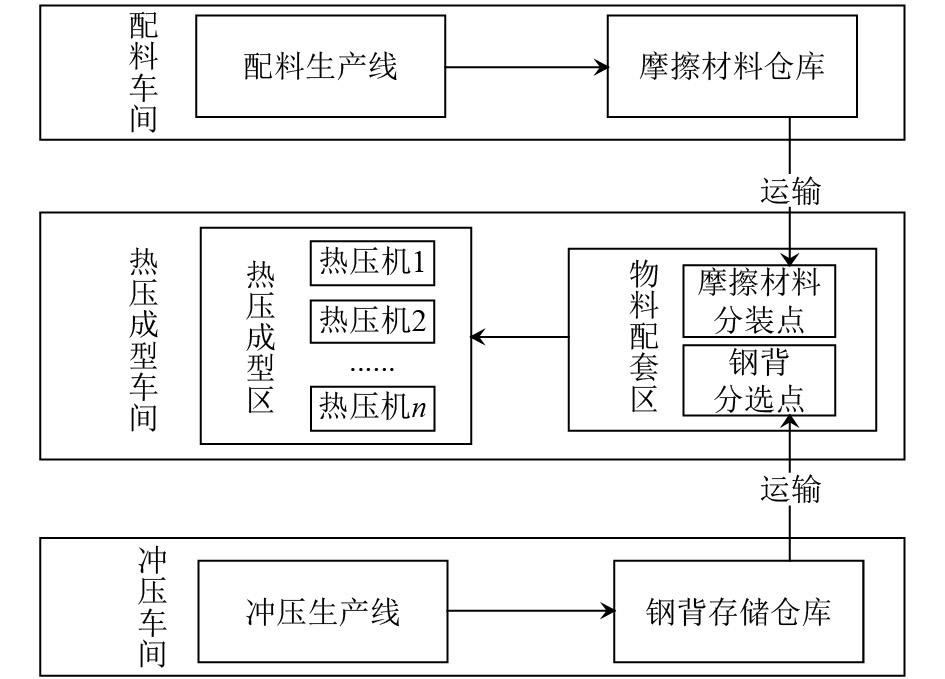
1 问题描述刹车片生产的主要工序有: 配料、冲压和热压成型, 其分别在配料车间、冲压车间和热压成型车间内进行. 其中配料和冲压工序是服务于热压成型工序, 另外配料车间和冲压车间有各自的配套仓库, 且生产设备少产量大, 可以直接使用针对热压车间生成的排产计划来提前指导配料车间和冲压车间的生产. 而热压成型工序时间较长, 且热压机数量多, 因此合理利用热压机对提高刹车片的产量至关重要. 因此, 本文重点对热压机的多品种变批次生产模式的排产问题进行研究. 刹车片生产主要的流程如图1所示.
|
图 1 刹车片生产主要流程 |
2 数学模型
在建立数学模型之前, 做出如下合理假设:
(1)在车间开始排产前, 车间单个生产班次的订单已经生成, 且不再发生变化.
(2)在热压机进行生产时, 各种物料已经齐套, 不需要考虑物料齐套的运输问题.
(3)在产品开始热压前需要一定的准备时间ts, 来调整热压机生产参数和热压配套工具等, 这里认为每种产品准备时间是相同的且热压机在生产不同的产品前都需要准备时间.
(4)每台热压机在生产过程中是连续生产的, 生产过程中不会出现中断.
(5)每一种产品在开始热压前, 热压工艺已经确定, 在单个生产班次中不会发生变化.
(6)在单个生产班次内生产的产品是没有优先级的.
(7)一个产品只能在一台热压机上生产一次.
2.1 目标函数刹车片生产计划的排产问题描述为: 有m台功能相同的热压机, n种不同的刹车片, 单个生产班次订单中每种刹车片的数量为
第i台热压机总的加工时间Ti为:
| $ {T_i} = \sum\limits_{j = 1}^n {{t_j}*c(j,i)} + \sum\limits_{j = 1}^n {x(j,i){t_s},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } i = 1,2,\cdots,m{\kern 1pt} $ | (1) |
式中, tj表示产品j的热压时间, 同型号刹车片在不同的热压机上生产时间是相同的; c(j, i) 表示产品j在热压机i上的生产数量; x(j, i)只有1和0两种取值, 产品j在热压机i上进行生产时等于1, 否则等于0; ts表示每种产品开始生产前的准备时间, 这里ts是常数.
则用时最长的热压机生产时间Tmax为:
| $ {T_{\max }} = \mathop {\max }\limits_i {T_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1,2,\cdots,m{\kern 1pt} $ | (2) |
本次排产设计的目标是获取整个生产过程最小加工时间的排产计划, 即求m台热压机中生产时间最长的热压机生产时间最小值, 因此目标函数为:
| $ \min ({T_{\max }}) $ | (3) |
本文建立的数学模型是由实际生产现场抽象而来, 所以该数学模型应该和实际生产现场一样会受到生产能力的约束[7,8], 其约束条件如下:
(1)机器加工时间约束:
| $ {T_i} \le {T_c},\begin{array}{*{20}{c}} {}&{i = 1,2, \cdots ,m} \end{array} $ | (4) |
式中, Tc表示单个生产班次内一台热压机允许的最长生产时间.
(2)每种产品的总数量约束: 在单个班次内, 每种产品生产的数量应该等于该生产班次订单中每种刹车片的数量, 即
| $ \sum\limits_{i = 1}^m {c(j,i)} = C_j^{\max },{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,n $ | (5) |
在产品种类和热压机数量比较少时, 目标函数的非线性程度低, 解空间比较小, 此时仅仅使用传统的遗传算法来求解排产问题, 能够得到比较理想的结果; 但在热压机数量比较多时, 目标函数的非线性程度和解空间都变的比较大, 很难得到比较理想的结果. 因此本文针对热压成型车间设计了一种联合均值-遗传算法来解决排产问题, 算法首先利用单个生产班次内分配在每台热压机上的理想加工时间进行排产, 即均值排产; 然后基于均值排产的结果再利用遗传算法继续排产, 即遗传算法排产. 较单纯使用遗传算法求解, 本文设计的联合均值-遗传算法将排产问题分两步进行求解, 能够有效的降低目标函数的非线性程度和解空间的复杂度, 从而得到比较理想的排产方案.
3.1 均值排产单个生产班次内分配在每台热压机上的理想加工时间是车间最小的整体生产时间, 所以将单个生产班次内分配在每台热压机上的理想加工时间作为最优方案的参考值. 为了减少生产准备时间和物料齐套运输的成本, 应该尽量让一种产品在一台机器上进行连续生产, 所以首先利用均值进行排产. 具体步骤如下:
(1)首先计算出单个生产班次内分配在每台热压机上理想的加工时间Tmean:
| $ {T_{\rm{mean}}} = \sum\limits_{j = 1}^n {\frac{{{t_j} \times C_j^{\max }}}{m}} + {t_s} $ | (6) |
(2)根据Tmean计算出在该时间段内能够连续生产产品j的最大数量Pj:
| $ {P_j} = \left\lceil {\frac{{({T_{\rm{mean}}} - {t_s})}}{{{t_j}}}} \right\rceil, \;\;j = 1,2,\cdots,n $ | (7) |
(3)Pj为在Tmean时间段中产品j在热压机连续生产的最大数量, 所以首先以Pj为指标进行均值排产.
| $ {H_j} = \left\lfloor {\frac{{C_j^{\max }}}{{{P_j}}}} \right\rfloor,\;\;j = 1,2,\cdots,n $ | (8) |
式中, Hj是产品j在均值排产过程中分配的热压机数目.
综上, 在均值排产过程中产品j已完成排产的数量Cj和m台热压机中已完成排产的总热压机数量f, 如式(9)所示. 剩余的没有在均值排产中排产的热压机与产品将由遗传算法进行排产.
| $ \left\{ {\begin{array}{*{20}{l}} {{C_j} = {P_j} \times {H_j}}\\ {f = \displaystyle\sum\limits_{j = 1}^n {{H_j}} } \end{array}} \right.,\;\;\;{j = 1,2,\cdots,n} $ | (9) |
经过均值排产后, 剩余的产品为
| $ {C_{j - left}} = C_j^{\max } - {C_j},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2,\cdots,n $ | (10) |
没有安排生产的热压机为
| $ {N_{\rm{left}}} = m - f $ | (11) |
此时, 利用遗传算法对剩余的机器和产品进行排产, 以获得最佳排产结果.
遗传算法的主要运算过程包括: 编码、选择、交叉、变异和迭代[9–11]. 编码是遗传算法的第一步, 是整个算法的基础, 目前比较流行的编码规则有, 矩阵编码、二进制编码、树形编码和量子比特编码等[12]. 结合由热压成型车间抽象出来的数学模型, 本文编码选择矩阵编码, 其归属于实数编码, 矩阵编码在求解大规模数据问题和高维度数据问题上具有明显的优势[13]. 选择的目的是在种群中选择合适个体, 常见的选择算子有锦标赛算法、随机遍历抽样法、比例选择、排序选择与无回访随机选择等. 本文以热压机生产时间为指标, 将锦标赛算法与随机遍历抽样法相结合来对种群进行选择, 这样能够在一定程度上保证在算法快速收敛的同时避免陷入局部最优. 交叉是模拟自然界生物杂交的过程, 通过个体间的染色体交叉, 会不断产生新的个体, 从而增加种群的多样性, 扩展问题的解空间. 目前几种比较常用的适用于实数编码的交叉算子有: 单点交叉、两点交叉、均匀交叉等[14]. 本文为了更好的模拟自然界的染色体交叉, 采用一种随机交叉方式. 变异是自然界的生物繁衍时发生的一种小概率事件, 在遗传算法中对种群中的个体进行变异的主要目的是保持种群的多样性, 同时在一定程度上防止算法陷入局部最优[15]. 最后一步是迭代, 通过迭代选择、交叉与变异, 选出最优个体.
具体的排产步骤如下:
(1)编码: 首先根据矩阵编码规则, 随机生成一个个体, 然后依照单个个体的编码规则, 随机生成一个种群. 单个矩阵的具体编码规则如下:
| $ \begin{array}{*{20}{c}} {c(1,f + 1)}& \cdots &{c(1,m)}\\ \vdots & \ddots & \vdots \\ {c(n,f + 1)}& \cdots &{c(n,m)} \end{array} $ |
在随机生成c(j, i)时, 随机数的生成范围通过单个生产班次理想生产时间Tmean来控制, 即满足:
| $ 0 \le c(j,i) < \left\lceil {\frac{{{T_{\rm{mean}}} - {t_s}}}{{{t_j}}}} \right\rceil, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots,m $ | (12) |
(2)选择: 按照概率Rg选出前Q个比较优秀的个体, 同时按概率Rb在除去前Q个体的种群中随机选择出比较差的个体. 由于是随机选择个体进入下一代, 无法具体控制下一代的种群数量, 因此本文设计的选择算子中的概率Rg具有一定的自适应性, 具体自适应规则为:
| $ {R_g} = \left\{ {\begin{array}{*{20}{c}} {{R_1},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S > IT}\\ {{R_2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S \le IT} \end{array}} \right.{\kern 1pt} {\kern 1pt} $ | (13) |
式中, R1、R2是两个常量概率, 且R1 < R2, S为当前迭代的种群数量, IT代表迭代开始时的初始迭代种群数量.
(3)交叉: 首先根据种群大小利用随机函数无放回的在种群中随机选取一对个体, 然后利用随机函数随机产生的交叉位置进行交叉, 最后重复上述过程, 直到整个种群全部完成交叉. 因为式(4)和式(5), 交叉时应该以矩阵的行为单位进行平行交叉, 即两个矩阵相同位置处的行进行互换. 以下为单次交叉的结果, 即随机选取的第j行个体进行了交叉.
| $ \begin{array}{c} \begin{array}{*{20}{c}} {{c_s}(1,f + 1)}&{{c_s}(1,f + 2)}& \cdots &{{c_s}(1,m)}\\ {}& \vdots &{}&{}\\ {{c_x}(j,f + 1)}&{{c_x}(j,f + 2)}& \cdots &{{c_x}(j,m)}\;\;\Leftrightarrow \\ {}& \vdots &{}&{}\\ {{c_s}(n,f + 1)}&{{c_s}(n,f + 2)}& \cdots &{{c_s}(n,m)} \end{array} \begin{array}{*{20}{l}} {{c_x}(1,f + 1)}&{{c_x}(1,f + 2)}& \cdots &{{c_x}(1,m)}\\ {}&\vdots &{}&{}\\ {{c_s}(j,f + 1)}&{{c_s}(j,f + 2)}& \cdots &{{c_s}(j,m)}\\ {}& \vdots &{}&{}\\ {{c_x}(n,f + 1)}&{{c_x}(n,f + 2)}& \cdots &{{c_x}(n,m)} \end{array} \end{array} $ |
其中, cs(j, i)和cx(j, i)代表随机选出的两个随机个体.
(4)变异: 首先使用概率Rb用来随机选取要进行变异的个体, 然后利用随机函数随机产生的变异位置进行变异. 同样因为式(4)和式(5), 变异的位置以行为单位.
(5)迭代: 综上4步, 在完成步骤(1)后, 通过循环按顺序反复进行(2)、(3)和(4)步骤, 通过Tmean值来动态控制迭代次数, 具体控制步骤如下:
| $ {T_{\max }} \le {T_{\rm{mean}}} + {T_d} $ | (14) |
| $ L \le {L_{\max }} $ | (15) |
式中, Td表示Tmax与Tmean最大允许偏差; L表示当前已经累计的迭代次数, Lmax表示最大允许的迭代次数. 如果循环同时满足式(14)和式(15), 表示已经产生最优解, 则停止循环, 取出最优解. 如果不满足式(15), 表示算法过早收敛, 则删除当前种群重新进行步骤(1)到步骤(5).
4 仿真实验与分析本文采用处理器为Intel i3-2348M的计算机, 利用Python在Spyder上进行仿真实验, 利用三个实例来验证算法的性能.
假设单个生产班次内一台热压机最大允许生产时间Tc = 400 min, 每种产品生产准备时间均为ts = 6 min, 排产实际时间与理想时间允许偏差Td = 9 min. 三个实例的具体参数如表1所示, 优化排产后的结果分别如表2、表3、表4和表5所示.
| 表 1 实例数据表 |
| 表 2 实例1排产计划 |
表2中前8台热压机排产结果是均值排产结果, 后2台是遗传算法排产结果. 在表3中前17台热压机排产结果是均值排产结果, 后3台是遗传算法排产结果. 在表4及表5中前25台热压机排产结果是均值排产结果, 后5台是遗传算法排产结果. 根据式(6)求得三个实例的理想生产时间Tmean分别为78 min、328.5 min和281 min. 而利用本文算法所得到的生产时间Tmax分别为83 min、335 min和286 min; 另外, 通过优化排产得到的生产时间与理想生产时间的偏差均小于9 min, 由此可见三个实例的排产结果都能够满足要求.
| 表 3 实例2排产计划 |
| 表 4 实例3排产计划(一) |
| 表 5 实例3排产计划(二) |
遗传算法是模仿自然界生物进化的仿生算法, 求解结果具有一定的随机性. 为了验证算法的稳定性, 本文对三个实例分别进行了100次仿真实验, 求得优化排产的生产时间与理想生产时间的平均误差如表6所示.
| 表 6 实际排产与理想排产时间差值表 |
从表6可见: 三个实例的平均误差都小于9 min, 所以本文设计的排产算法是稳定的.
5 结束语本文设计了一种联合均值-遗传算法来解决刹车片生产计划的排产问题. 首先对热压成型车间的实际生产现状进行分析, 建立了相应的生产数学模型, 然后针对已经建立的数学模型, 设计了利用联合均值-遗传算法进行排产的优化方案, 最后利用三个实例验证了算法的性能, 得出本文设计的排产方案可以有效地应用于热压成型车间.
| [1] |
王爱民. 制造执行系统(MES)实现原理与技术. 北京: 北京理工大学出版社, 2014. 11–21.
|
| [2] |
蒋海峰. 多品种少批量生产线排产软件的设计与实现[硕士学位论文]. 大连: 大连理工大学, 2017.
|
| [3] |
刘晨, 蒙丹花, 方玮宸, 等. 多品种小批量订单型企业生产调度优化. 包装工程, 2016, 37(11): 93-99. |
| [4] |
孟巧凤, 张林鍹, 董杰涛, 等. 混流柔性生产线排产优化. 计算机仿真, 2016, 33(7): 245-250. |
| [5] |
武韶敏, 胡晓兵, 王江武, 等. 改进遗传算法求解面向订单多目标排产问题. 机械设计与制造, 2018(3): 102-104, 108. |
| [6] |
金剑, 金钊, 祁跃东. 卷烟生产计划排产模型建立与优化. 计算机工程与应用, 2013, 49(18): 253-259. |
| [7] |
姚丽丽, 史海波, 刘昶, 等. 烟草排产中嵌入规则的遗传算法应用研究. 制造业自动化, 2011, 33(4): 89-93. |
| [8] |
王博. 液压缸基础零件制造车间MES的研究与设计[硕士学位论文]. 南京: 南京理工大学, 2017.
|
| [9] |
吕文军. 基于BOM的柔性作业车间调度方法与信息系统研究[硕士学位论文]. 重庆: 重庆大学, 2016.
|
| [10] |
王明星, 李利民. 改进的遗传算法在机加车间排产优化的研究. 制造业自动化, 2014, 36(8): 34-37, 48. |
| [11] |
张国庆, 刘永进, 梅中义. 改进的遗传算法在复合材料车间计划排产中的应用研究. 现代制造工程, 2010(7): 56-59. |
| [12] |
张超群, 郑建国, 钱洁. 遗传算法编码方案比较. 计算机应用研究, 2011, 28(3): 819-822. |
| [13] |
陆远, 尹建定. 智能制造车间设备动态能力分析技术研究. 机床与液压, 2018, 46(1): 1-6. |
| [14] |
李书全, 孙雪, 孙德辉, 等. 遗传算法中的交叉算子的述评. 计算机工程与应用, 2012, 48(1): 36-39. |
| [15] |
孙羽. 基于遗传算法的生产计划调度系统设计与实现[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
 2019, Vol. 28
2019, Vol. 28


