随着信息技术的不断发展, 网络教学已经成为一种重要的学习方式, 根据文献[1]统计的数据, 截止到2016年年底, 我国在线学习的用户数已经超过了1.38亿, 和2015年相比增加了2750万人, 年增长率为25%. 由于网络学习本身的特点, 从教师的角度出发, 存在无法及时有效掌控学习者的学习状态和能力程度, 从而无法做出有效的教学干预和调整. 从学习者的角度出发, 对于自己的学习进展、能力提升、掌握程度缺乏精准的量化依据. 由此可见, 在网络学习逐渐普及的今天, 如何对在线学习用户的成绩进行分析预测, 并根据预测结果对学习者提出相应的学业建议或学业预警, 从而保证在线学习者的学习效率和质量, 已经成为网络教学平台是否能够继续发展的关键问题. 本文通过分析学习者在网络教学平台上的日常学习数据和最终学习成绩的关系, 采用学习向量化神经网络(Learning Vevtor Quantization, LVQ)对不同类型的学习者数据样本进行分类, 同时采用遗传算法(Genetic Algorithm, GA)作为BP (Back Propagation)神经网络的学习算法, 建立基于遗传算法GA的BP神经网络的在线学习学业成绩预测模型, 并验证其准确性和收敛速度. 最后的实验结果表明: 与其他的方法相比, 利用该方法建立的预测模型能够有效提高在线学习者的学业成绩预测精度, 根据参数的调整还能显著提高神经网络的训练速度和收敛性, 为在线学习者是否进行学业预警和调整教学策略提供量化依据, 具备一定的工程应用价值.
1 在线学习行为特性分析 1.1 目前研究现状Ohia等人提出了采集学业成绩相关数据的六步模型-FAMOUS, 注重实现六个关键步骤[2], 文献[3]从学习行为分析和学习结果分类设计了学业成绩预测框架. 文献[4]提出将课程、课堂、课外三者进行综合之后形成“三位一体”学业预警机制. Arsad等人使用人工神经网络, 利用学习绩点作为输入输出的方法来预测工程学专业学生的学业成绩[5]; 文献[6]利用离群点检测的学生学习状态分析方法, 对学生的历史成绩数据进行二次挖掘, 以此判断成绩的变化. 文献[7]在数据挖掘的基础上, 以聚类分析为核心对网络学习过程进行监管, 从数据的历史变化中预测学生的学习效果. 文献[8]建立了一个三层神经网络, 包含17个输入结点, 7个隐藏结点, 1个输出结点, 用来对学生的学业成绩进行预测. 文献[9]提出了学习分析循环模型, 包括学习过程的搜集、存储、数据的清洗、整合、分析等部分, 将学习的各个环节融为一个整体. 文献[10]通过分析学习过程及其学习者心态分析, 提出了如何改善学习效率的模型, 其中的信息处理模块涵盖了学生成绩的整合及预测, 通过知识应用模块来对其进行进一步的分析和优化.
通过文献分析发现国内外研究者对于在线学习行为及其成绩的分析预测已经做了不少的研究工作, 但是经过归类分析可以发现: 以上部分研究属于工作模型, 主要基于理论演绎推导和经验预测, 缺少以学习者的学习行为、成绩分布、能力层次为核心分析对象的计算模型. 大部分侧重于对于数据的二次挖掘分析, 缺少学习者其他相关关键特征数据的关联分析. 采取神经网络进行预测的部分研究往往侧重于单一的分类器模式, 并没有真正把神经网络的学习机制应用到学业成绩的分析预测.
1.2 在线学习成绩特性分析在线学习行为具有一定的随机性和间歇性, 其行为受到多方面情境的影响, 通过历史数据的分析比对, 对于在线学习成绩影响的因素比较多, 但是最重要的影响因素主要有三类, 分别是“学习特征”、“个人情感”、“学习环境”, 对于不同层次和类型的学习者, 这三类因素对学习的影响是比较大的, 也是具有共性的, 本文对以上三个因素又进行了进一步的细分, 将一个主因素划分成三个辅因素, 如图1所示, 我们将这些影响学习者最终成绩的因素称之为“情境分类”.
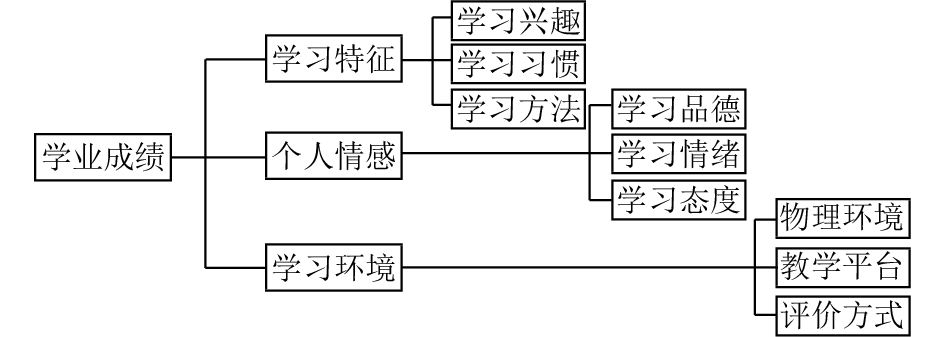
|
图 1 在线学习学业成绩情境分类 |
在实际应用中, 每种情境对于学业成绩的影响程度都是不一样的, 但是总体上呈现一定的规律, 为了更好的衡量每一种情境对学业成绩的影响, 根据现有教学平台的数据, 本文对每一个影响因素对学业成绩的影响做了统计分析(以12个月的数据为例), 具体结果如图2所示.
测试数据来源于我校全部学生使用的网络教学平台为主, 参加测评的学生一共1000人, 分别在网络平台注册账号完成课程的完整学习过程. 从图2可以看出, 在“学习特征”部分, “学习方法”对于学业成绩的影响高于“学习习惯”和“学习兴趣”, 这说明有效的学习方法能够对最后成绩的获得达到事半功倍的效果. 在“个人情感”部分, “学习态度”对学业成绩有着决定性的作用, 而“学习品德”和“学习情绪”对成绩的影响微乎其微, 这说明良好的学习态度对于网络教学这种松散型的教学方式显得尤为重要, 而“学习品德”和“学习情绪”由于主观成分较大, 且在某些方面受制于“学习态度”, 所以在测试结果中表现出来的影响值并不是那么强烈. 在“学习环境”方面, 可以看到有影响作用的是“评价方式”和“教学平台”, 这说明, “教学平台”用户体验程度的优劣、用户界面的友好程度对于学习者最终的成绩也是有一定的影响作用的, 至于“评价方式”这种在传统教学方式中显得比较“鸡肋”的功能, 在在线学习中却变得尤为重要, 这可能取决于两方面的因素, 一是由于在线学习的特殊性, 教师和学生很难做到日常的交流, 所以学生对教师的授课方式或者讲解的难易程度的要求只能以“在线评价”的方式给出, 另外, 在线学习的另外特点是“铁打的平台, 流水的教师”, 教师质量的把握很大一方面也是通过学生对其进行评价来衡量的, 所以, “评价方式”的优劣和设置是否科学对学生的成绩也是有着很大的作用, 这要求在线学习平台设计者除了注重开设的课程科目之外, 还要对在线学习平台上的服务型资源加以重视, 以期学生能够在平台上获得更好的学习成绩.
2 网络教学学业成绩预测模型设计 2.1 基于LVQ神经网络预测模型由1.2节的分析可以看出, 不同的情境因素对学业成绩有较大的影响, 其中“学习方法”、“学习态度”和“评价方式”对学业成绩的影响最为显著, 本文把这三个情境元素归类为广义的“能力层次”样本, 利用LVQ神经网络对样本进行分类, 然后按照分类后的样本进行训练, 最后利用遗传算法在BP神经网络的基础上建立学业成绩预测模型. 具体实现方式如图3所示, 模型算法的核心在于利用LVQ神经网络对样本进行分类, 模型对样本按照学习行为、学习目标、学习活动参与度三方面来进行分类.
2.2 LVQ网络结构LVQ神经网络在竞争网络结构的基础上提出的, 它融合了竞争学习思想和有监督学习算法的特点, 对输入样本的分配类别进行规定, 从而克服自组织网络采用无监督学习算法带来的缺乏分类信息的弱点, 其网络结构如图4所示, 竞争层有m个神经元, 输入层有n个神经元, 两层之间完全连接. 输出层每个神经元只与竞争层中的一组神经元连接, 连接权重固定为1, 训练过程中输入层和竞争层之间的权值逐渐被调整为聚类中心. 当一个样本输入到LVQ网络时, 竞争层的神经元通过“胜者为王学习规则”产生获胜神经元, 允许其输出为1, 其它神经元输出为0. 与获胜神经元所在组相连的输出神经元输出为1, 而其它输出神经元为0, 从而给出当前输入样本的模式类. 将竞争层学习得到的类成为子类, 而将输出层学习得到的类成为目标类, 以达到输入样本分类的目的.

|
图 2 各种情境因素对学业成绩的影响 |
设输入层的输入向量定义为
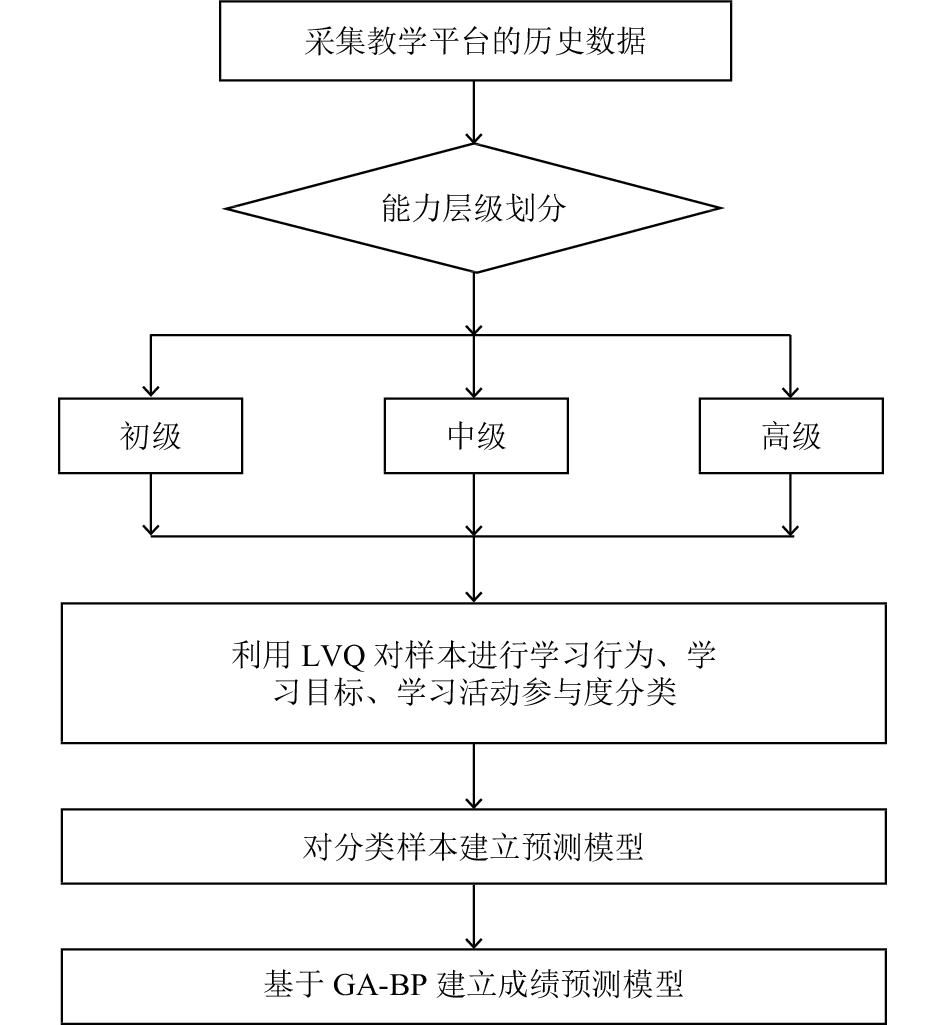
|
图 3 在线学习学业成绩预测流程图 |
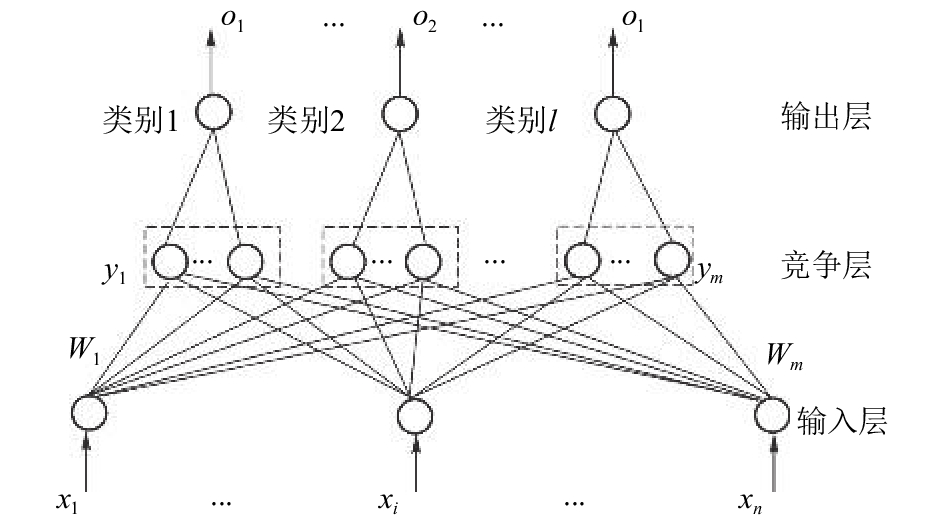
|
图 4 LVQ网络结构图 |
LVQ神经网络训练的步骤如图5所示.
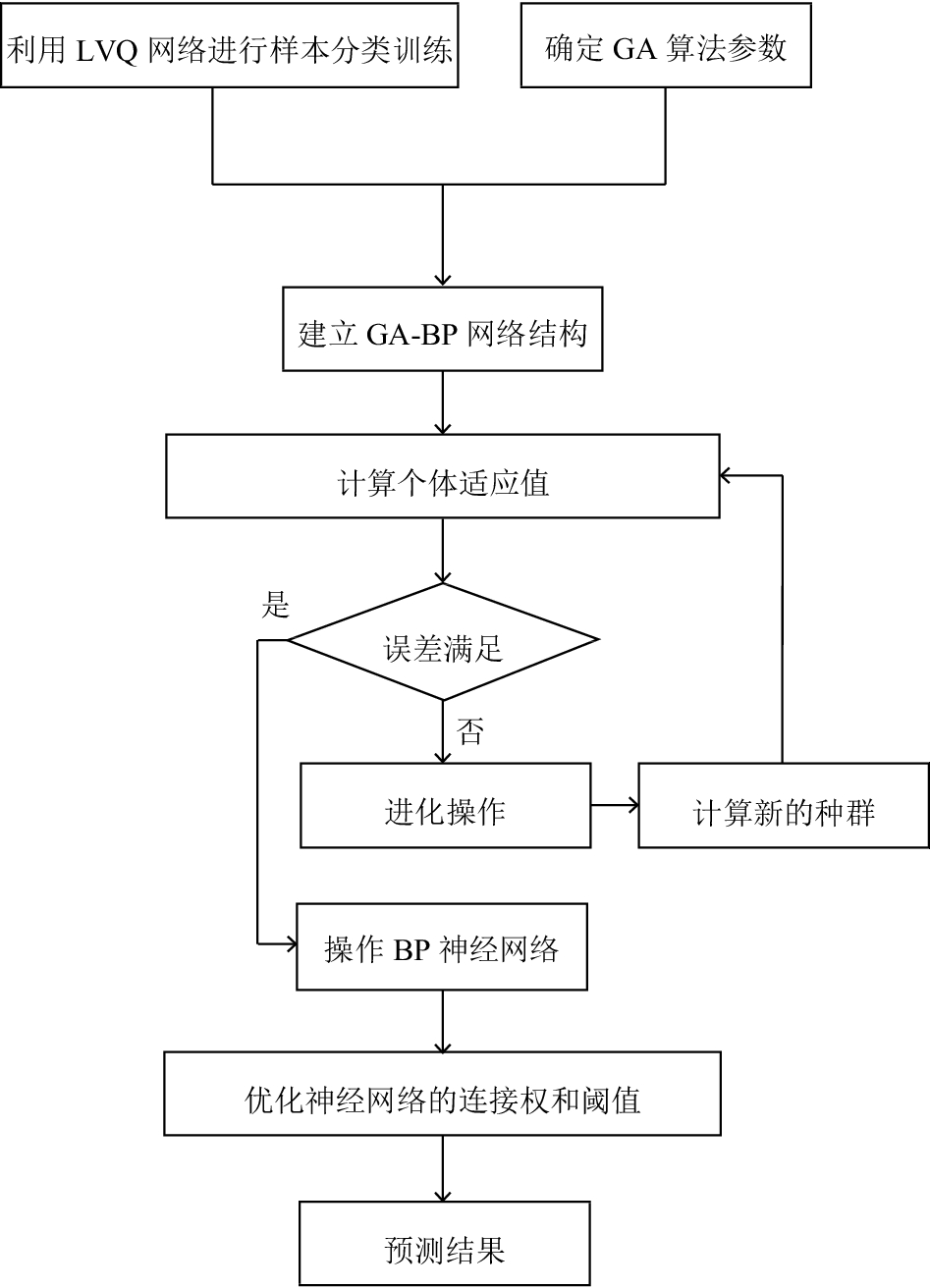
2.3 采用GA算法的BP神经网络BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络. 它的基本思想是梯度下降法, 利用梯度搜索技术, 以期使网络的实际输出值和期望输出值的误差均方差为最小, 但是BP神经网络容易陷入局部最小值. 而遗传算法的优化搜索方法在计算时并不依赖于梯度信息, 而只需要影响搜索方向的目标函数和相应的适应度函数, 不依赖于问题的具体领域, 在求解最优解方面能够弥补BP神经网络容易陷入局部最小值的问题. 本文的主要工作亮点利用在于利用LVQ神经网络学习分类, 然后将BP网络和GA算法结合起来对在线学习行为的学业成绩进行预测. 之所以这么做的原因主要考虑两方面因素: 第一, 如果只是单纯的采用BP网络, 由于网络本身的结构导致适应过程和全局逼近比较耗时, 导致网络的收敛速度会变慢. 另外BP神经网络算法本身属于梯度下降, 容易陷入局部最优的错误模式. 第二, GA是一种自适应优化方法, 以样本适应度函数为基础, 可以在全局解空间的多个区域内采用随机方法寻求最优解, 这刚好弥补了BP神经网络的缺陷. 考虑到二者的特点, 将他们结合起来是一种提高预测精准率的策略. 其具体实现方式如图6所示.
2.4 采用GA算法进行网络优化算法的过程将GA与BP网络进行结合, 本质上是利用了种群搜索的方式对BP神经网络的权值、阈值进行最优化的配置, 以寻找最容易获得全局最优的参数, 目的是为了改变BP神经网络过度依赖梯度信息的问题. 其实现的关键过程如下所示.
(1) 基因表述
这一步的主要工作是为了确定网络的权值和阈值的编码, 将其作为一组有序染色体, 用相应维数的实属变量表示, 完成编码过程, 提高运算效率, 经过编码后的基因可以如式(1)表示:
| $X = \left[ \begin{array}{l} {w_1}_1,{w_{12}}, \cdot \cdot \cdot ,{w_{mn}},,{v_{11}},{v_{12}}, \cdot \cdot \cdot ,{v_{pm}},\\ {\theta _1},{\theta _2}, \cdot \cdot \cdot ,{\theta _m},{t_1},{t_2}, \cdot \cdot \cdot ,{t_p} \end{array} \right]$ | (1) |
(2) 个体适应度的表示
这一步的主要工作是为了完成对第一步中染色体的评价工作, 根据个体所对应的神经网络计算出BP神经网络的误差平方和, 并采用误差平方和的倒数来表示, 如式(2)表示:
| $E\left( {{X_i}} \right) = \frac{1}{{2m}}\sum\limits_{k - 1}^m {\sum\limits_{j = 1}^n {{{\left( {d_{kj}^i - o_{kj}^i} \right)}^2}} } $ | (2) |
其中,
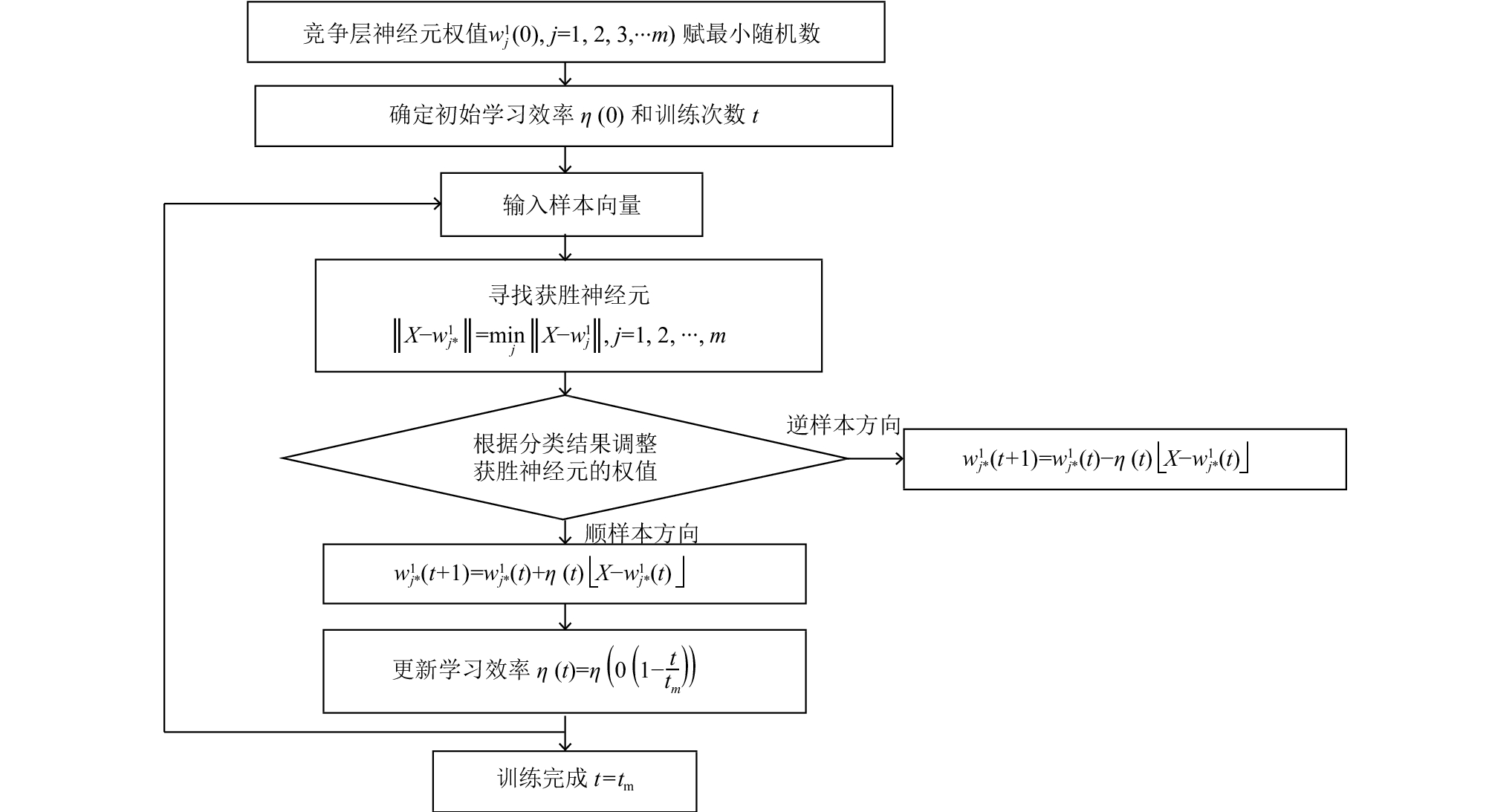
|
图 5 LVQ神经网络训练过程 |
|
图 6 基于GA-BP神经网络的预测过程 |
(3) 运用进化操作算子
假设两个基因链为
| $\begin{array}{l} \delta _i^m = \left\{ \begin{array}{l} \min \left\{ {{y_i} + \dfrac{{1 + {p_c}}}{2}\left( {{y_i} - {y_j}} \right),\;{y^{\max }}} \right\}\\ \max \left\{ {{x_i} + \dfrac{{1 + {p_c}}}{2}\left( {{y_i} - {y_j}} \right),\;{y^{\min }}} \right\} \end{array} \right\}\\ \delta _j^m = \left\{ \begin{array}{l} \min \left\{ {{y_j} + \dfrac{{1 + {p_c}}}{2}\left( {{y_j} - {y_i}} \right),\;{y^{\min }}} \right\}\\ \max \left\{ {{x_j} + \dfrac{{1 + {p_c}}}{2}\left( {{y_j} - {y_i}} \right),\;{y^{\max }}} \right\} \end{array} \right\} \end{array}$ | (3) |
交叉后的新个体如式(4)表示[11]:
| $\left\{\begin{array}{l} {x_i} = \dfrac{{1 + {p_c}}}{2}\delta _i^m + \dfrac{{1 + {p_c}}}{2}\delta _j^m\\ {x_j} = \alpha {y_i} + \left( {1 - \alpha } \right){y_j} \end{array}\right.$ | (4) |
式(4)中的交叉运算保证了子代既可以在其父代所处的区域之间搜索, 也可以在适应度更高的方向搜索更适合的区域, 既保证搜索的多样性, 又提高搜索的效率.
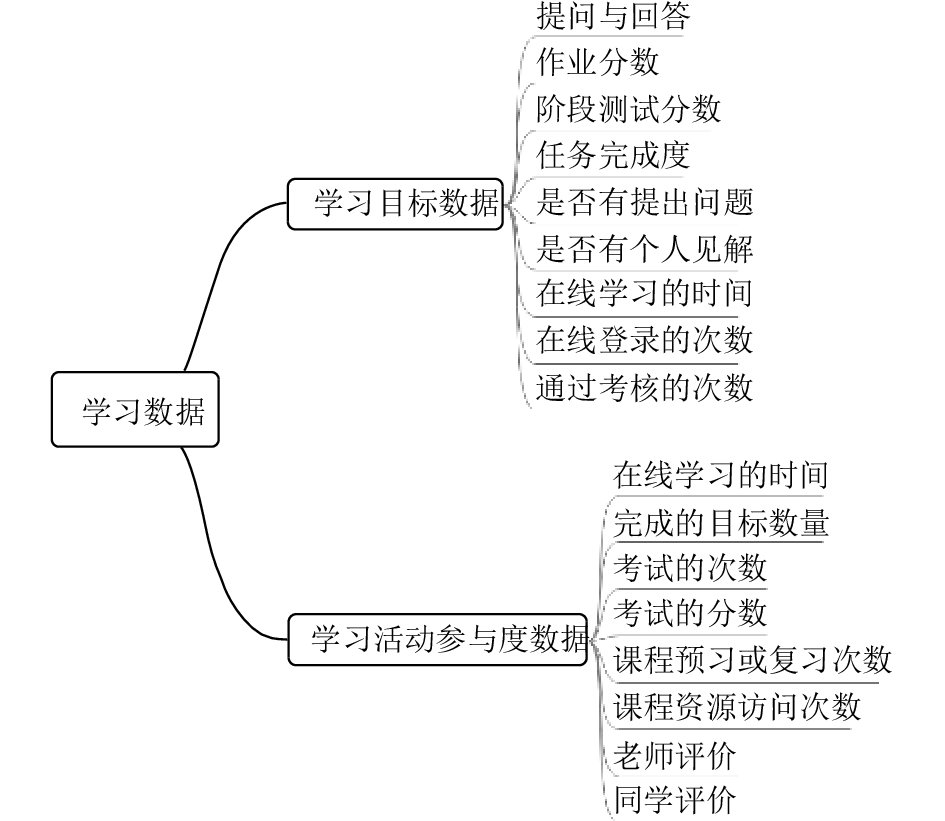
3 预测实例及分析以我校网络教学平台1000名学生在半年内的阶段学习数据为研究对象, 由于平台上记录的数据没有规则, 为了尽量提高学业成绩预测的准确性, 在采集数据的时候从这几个方面作为学业成绩预测的属性因素, 具体见图7所示.
本文采用平均绝对误差百分比MAPE和均方根误差RMSE对在线学习学业成绩预测进行评估, 其中,MAPE用来衡量一个模型预测结果的好坏, RMSE用来反映预测的精准度, 分别如式(5)(6)表示:
| $ MAPE{\rm{ = }}\dfrac{{sum\left( {\dfrac{{\left| {{y^*} - y} \right| \times 100}}{y}} \right)}}{n} $ | (5) |
|
图 7 网络教学平台学习数据的影响因子 |
| $ RMSE = \sqrt {\dfrac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{X_{{\rm {obs}},i}} - {X_{{\rm{model}},i}}} \right)}^2}} }}{n}} $ | (6) |
其中, y*和y分别代表预测值和实际值, n代表样本数量. Xobs和Xmodel分别代表观测值和实际值.
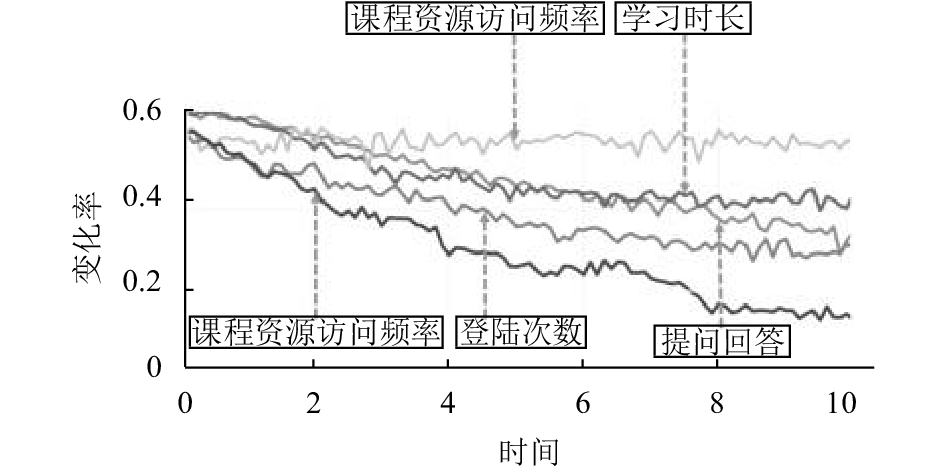
在实际测试中, 以每天为单位对数据进行归一化处理, 学习者每天学习的情况受不同影响因子的作用, 参看图7. 为了测试结果公平, 我们统一将每天的影响因子归结为五类, 为了公平起见, 选取影响因子的标准是尽可能的满足所有状态学习的变化, 通过大量的实验测试, 我们选取作业分数、提问回答、登录次数、学习时长、课程资源访问频率五个因素, 具体的表现关系如图8所示.
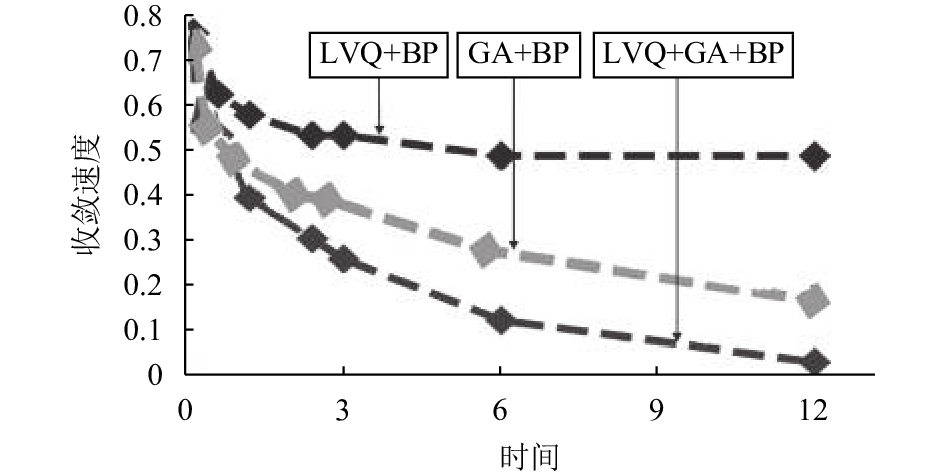
从图8中可以看出, 这五种影响因子的变化规律对每个学习者基本呈现相同的规律, 可以用作统计参数使用. 每天的实际影响因子表现为它们的不同组合. 用前一日的学习数据按一定的权重比例加上当天的影响因子构成完整的数据作为训练样本, 训练目标以当日的数据为基本单位, 用当日的测试数据及后一日的学习状态影响因子来预测后一日的学习成绩, 依次迭代下去. 以完成的任务学时作为窗口长度, 对在线学习时间序列进行移位加窗分析, 依次移动窗口, 直至选定足够多的训练样本和目标, 在LVQ-GA-BP网络中进行训练, 然后用此网络模型依次学习数据进行预测, 从而得到学业成绩的总体预测. 在实际训练中, 网络的隐层节点为15, 基因长度为426, 种群规模为50, 遗传代数为150, 学习速率设为0.1, 最大迭代次数为1000次. 为了验证本文提出的方法在收敛速度和计算精度上的改进, 采用了两种模型与之对比, 第一种是只采用遗传算法的BP神经网络, 第二种是没有采用遗传算法的LVQ网络与BP网络相结合. 图9表示的是三种网络结构的收敛速度, 可以看到LVQ+GA+BP的收敛速度明显快于其他两种.
|
图 8 在线学习影响因子的变化状态 |
|
图 9 三种模型运算收敛速度 |
为了验证预测结果与真实成绩走向之间的关系, 我们分别选取了当年数据(2016年)和近4年的数据(2012–2016年), 在本文设计的网络中进行训练学习, 得到的结果如图10和图11所示、在图10中, 点状虚线表示真实的成绩变化走向, 深色实线表示没有采用LVQ的GA+BP神经网络的训练预测结果, 浅色实线表示本文中提出的LVQ+GA+BP神经网络训练预测结果. 图11表示采用的是年度数据预测, 虚线表示真实的成绩分布趋向, 实线表示利用本文方法得到的成绩预测趋向. 从两图的结果可以看出, 无论是年度数据还是历年数据, 本文设计的网络结构都能够很好的符合真实成绩的变化趋势, 在学业成绩预测方面具有一定的可信度. 利用式(5)和(6)分别计算三种模型的MAPE和RMSE值, 结果如表1所示.
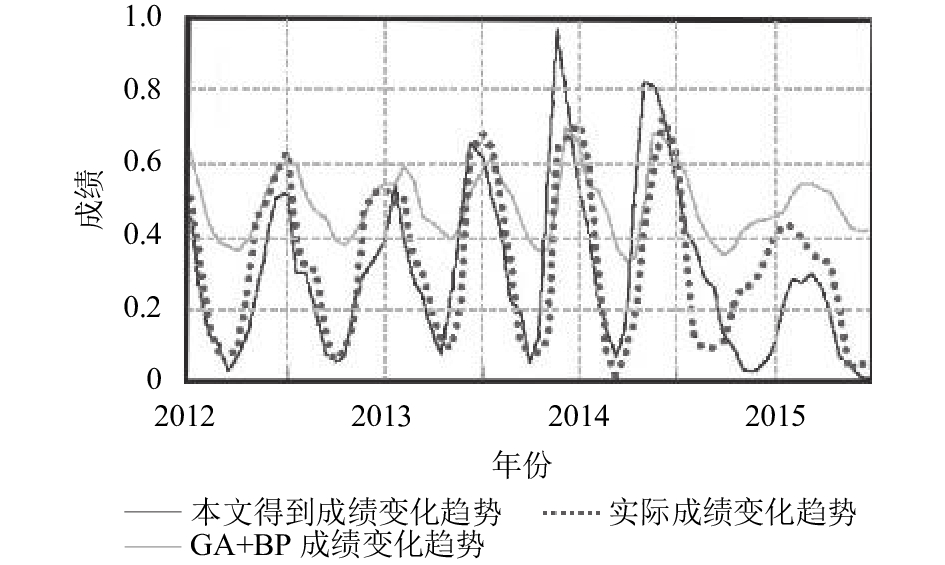
|
图 10 历年学业成绩变化趋势图 |
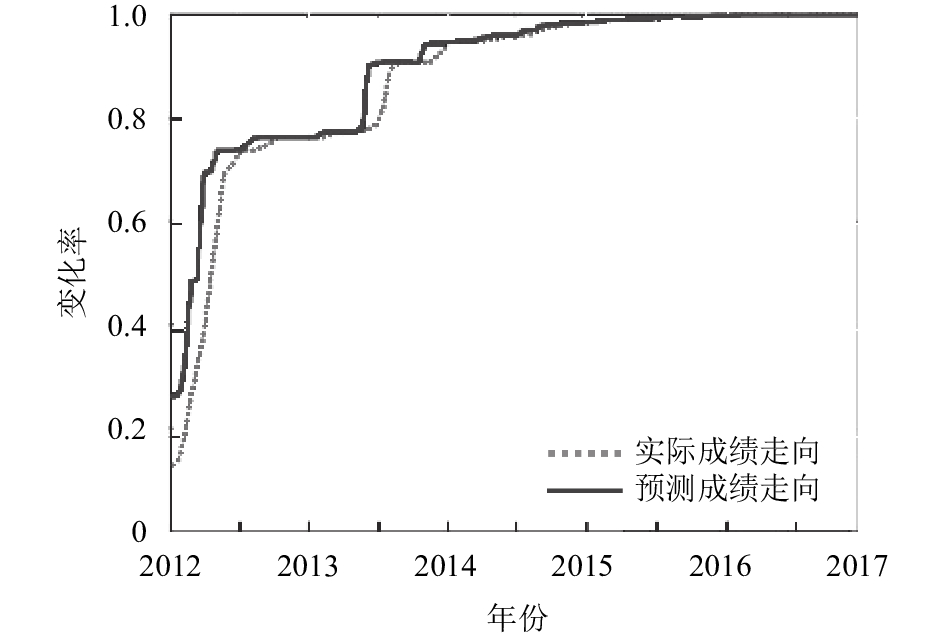
|
图 11 年度学业成绩变化趋势图 |
| 表 1 三种预测模型的结果评估(单位: %) |
从表1可以看出, 采用LVQ的网络进行样本分类以后, MAPE和RMSE的值显著下降, 这表明LVQ前期样本分类结果对于模型最后的结果预测有重要的影响作用, 而采用GA算法以后, 可以更进一步的优化两者的值, 使得预测精度更加精确.
4 结论与展望在互联网极度发达的今天, 网络在线学习已经成为传统教育的重要补充部分, 利用学习者的特征数据进行学习分析并对其学习成绩进行有效预测, 可以及时发现学习过程中存在的问题和障碍, 为进行适当的学习干预提供精准化的数据支持, 这是传统教育无法做到的一点. 本文构建三者合一的神经网络模型, 利用现有数据对学生的学习成绩做出预测, 实验结果表明, 使用本文提出的网络模型进行预测得到的成绩与真实成绩的分布基本一致, 预测精度具有很高的可信度. 在后期的研究中, 我们将依据现有的模型和框架, 利用可视化的方式对学生的学习活动和学业成绩之间的关系进行呈现, 为更加有效的提供在线学习精准化分析提供科学依据.
| [1] |
中国互联网络信息中心. 中国互联网络发展状况统计报告. 北京: 中国互联网络信息发展中心, 2018.
|
| [2] |
Ohia UO. A model for effectively assessing student learning outcomes. Contemporary Issues in Education Research, 2011, 4(3): 25-32. DOI:10.19030/cier.v4i3 |
| [3] |
武法提, 牟智佳. 基于学习者个性行为分析的学习结果预测框架设计研究. 中国电化教育, 2016(1): 41-48. DOI:10.3969/j.issn.1006-9860.2016.01.006 |
| [4] |
金义富, 吴涛, 张子石, 等. 大数据环境下学业预警系统设计与分析. 中国电化教育, 2016(2): 69-73. DOI:10.3969/j.issn.1006-9860.2016.02.010 |
| [5] |
Arsad PM, Buniyamin N, Manan JLA. A neural network students’ performance prediction model (NNSPPM). 2013 IEEE International Conference on Smart Instrumentation, Measurement and Applications. Kuala Lumpur, Malaysia. 2013. 1–5.
|
| [6] |
陆柳生, 余明晖. 基于离群点检测的学生学习状态分析方法. 计算机与现代化, 2016(3): 35-40. DOI:10.3969/j.issn. |
| [7] |
施佺, 钱源, 孙玲, 等. 基于教育数据挖掘的网络学习过程监管研究. 现代教育技术, 2016, 23(6): 87-93. DOI:10.3969/j.issn.1009-8097.2016.06.014 |
| [8] |
舒忠梅, 屈琼斐. 基于教育数据挖掘的大学生学习成果分析. 东北大学学报(社会科学版), 2014, 16(3): 309-314. |
| [9] |
Siemens G. Learning analytics: The emergence of a discipline. American Behavioral Scientist, 2013, 57(10): 1380-1400. DOI:10.1177/0002764213498851 |
| [10] |
Kardan AA, Ebrahim MA, Imani MB. A new personalized learning path generation method: ACO-Map. Indian Journal of Scientific Research, 2014, 5(1): 17-24. |
| [11] |
Back B, Laitinen T, Sere K. Neural networks and genetic algorithms for bankruptcy predictions. Expert Systems with Applications, 1996, 11(4): 407-413. DOI:10.1016/S0957-4174(96)00055-3 |
 2019, Vol. 28
2019, Vol. 28



