2. 中北大学 电子测试技术国防科技重点实验室, 太原030051;
3. 中北大学 信息探测与处理山西省重点实验室, 太原 030051
Key Laboratory of National Defense Science for Electronic Measurement Technology, North University of China, Taiyuan 030051, China;
Shanxi Key Laboratory of Instrumentation Science and Dynamic Measurement, North University of China, Taiyuan 030051, China
在设计基于FPGA的数字图像处理系统时, 有两种主要的实现方式: 一种是传统的基于硬件描述语言(HDL)的开发方法, 另一种是基于图形化设计工具的实现方法[1–3]. 传统的开发方式采用层次化和模块化的设计思路, 通过编写HDL代码和调用IP核来描述处理过程. 这种设计方法需要编写大量代码, 并且工作量很大[4]. 调试时间长, 重复劳动严重, 对算法处理模块仿真的结果也只能是时钟沿和海量的数字信息组成的时序, 若要得到直观的图像处理结果, 还需要进行预存数据、虚拟数据传输接口、数据结果分析等后续工作, 导致系统开发周期大大延长. 而图形化编程方式的出现为FPGA设计提供了新的设计思路, 这种方法使用人们熟悉的图标表达设计内容, 使用连线来表示子系统之间的互动关系, 开发者可以通过直观的可视化操作完成处理算法的搭建[5]. 相比传统的开发方式, 图形化编程简单直接, 易于理解, 由计算机负责对代码的编写, 避免了人为错误的引入, 大大提升了开发效率.
常用的图形化编程工具包括NI公司的LabView、若贝公司的Robei、Altera公司的Dsp Builder和Xinlinx公司的System Generator等[6,7]. 基于这些开发工具, 国内外对FPGA的图形化编程有过很多较为深入的研究. 比如: 高静等通过LabVIEW图形化编程实现了增量式数字PID控制算法[8]; 马涛, 陈娟等利用系统工具DSP Builder给出了数字下变频器的FPGA设计方法[9]. 郭俊位等针对USDR软件无线平台基于simulink环境设计了一套FPGA图形化设计工具为算法工程师扫除了硬件编程的障碍[10]. 本文基于System Generator工具, Sobel算子作为图像边缘检测中最重要的算子之一, 在机器学习、数字媒体、计算机视觉等信息科技领域起着举足轻重的作用[11,12], 以Sobel边缘检测算法为例, 在Matlab/Simulink平台搭建了数字图像处理系统, 完成了该算法的图形化建模及在线仿真并对系统进行了功能验证和测试结果分析.
1 System Generator概述System Generator是Xinlinx公司推出的一款基于Matlab/simulink平台的图形化设计工具, 目的是为了简化传统的FPGA开发流程. 它为硬件设计提供了合适的数字图像处理建模环境, 可以使得基于FPGA的数字信号处理系统硬件的设计开发变的简单快捷[13–15]. System Generator可以看作是Matlab环境下的硬件设计工具包, 内部提供了丰富的子模块, 用户只需通过拖拽和连接子模块就可以搭建数字系统, 最后把模型化的设计结果通过编译器直接转化为硬件描述语言, 再通过ISE软件综合、布线等过程即可完成算法模块的硬件设计. 这样的设计方法已在许多大型复杂的系统中体现出巨大的优势和强大的潜能, 借助于这个高层次的图形化设计工具, 我们可以对数字信号的处理算法进行系统建模并将图形化的设计模型直接编译为硬件设计结果, 从而成功连接了高层次的算法设计与硬件描述工具.
2 Sobel边缘检测算法及其基于System Gen-erator的实现 2.1 sobel边缘检测算法图像边缘检测是计算机视觉和数字图像处理研究领域的基础概念, 边缘指的是数字图像矩阵中灰度急剧变化的边界. 它是图像分析和理解的重要基础, 如区分目标与背景, 分析目标纹理特征和形状特征[16]. 研究者们根据图像边缘处灰度值突变的特点提出了多种以一阶导数为基础的梯度算子.
索贝尔算子(Sobel operator)是边缘检测中常用的算子之一, 分别为横向和纵向, 它们的模版分别为:
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{ - 1}}}&{\rm{0}}&{\rm{1}}\\ {{\rm{ - 2}}}&{\rm{0}}&{\rm{2}}\\ {{\rm{ - 1}}}&{\rm{0}}&{\rm{1}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\rm{ - 1}}}&{{\rm{ - 2}}}&{{\rm{ - 1}}}\\ {\rm{0}}&{\rm{0}}&{\rm{0}}\\ {\rm{1}}&{\rm{2}}&{\rm{1}} \end{array}} \right] $ |
Sobel横向算子 Sobel纵向算子
这种离散型的差分算子, 对图像的每个像素以检测像素点为中心, 考察其3×3领域内像素灰度的加权差, 根据该点是否处于极值状态进行边缘检测, 其本质上是一种梯度的幅度, 通过选取适当的门限, 当大于门限时判定为边缘点[17].
| $ {G_x} = \left[ {\begin{array}{*{20}{c}} {{\rm{ - }}1}&0&{\rm{1}}\\ {{\rm{ - 2}}}&{\rm{0}}&{\rm{2}}\\ {{\rm{ - 1}}}&{\rm{0}}&{\rm{1}} \end{array}} \right] * A $ | (1) |
| $ {G_y} = \left[ {\begin{array}{*{20}{c}} {{\rm{ - }}1}&{{\rm{ - }}2}&{{\rm{ - }}1}\\ 0&0&0\\ 1&2&1 \end{array}} \right] * A $ | (2) |
其中, Gx表示基于横向算子的滤波结果, Gy表示基于纵向算子的滤波结果.A表示由检测到的元素周围的3×3阵列中的所有元素组成的矩阵[18].
设A矩阵中处于3×3矩阵正中间的元素为g(x,y), 则A可以表示为:
| $ \left[ {\begin{array}{*{20}{c}} {g(x - 1,y - 1)}&{g(x,y - 1)}&{g(x + 1,y - 1)}\\ {g(x - 1,y)}&{{{g}}(x,y)}&{g(x + 1,y)}\\ {g(x - 1,y + 1)}&{g(x,y + 1)}&{g(x + 1,y + 1)} \end{array}} \right] $ | (3) |
将式 (3) 分别带入 (1), (2)得:
| $ \begin{array}{l} {{{G}}_x} = [{{g}}(x - 1,y - 1) - g(x + 1,y - 1)]\\ \;\;\;\;\;\;\;\;\;{\kern 1pt} + 2 \times [g(x - 1,y) - g(x + 1,y)]{\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {\kern 1pt} \;\;\;\;\;\;\;\;\; +[g(x - 1,y + {{1}}){{ - g}}(x + 1,y + 1)] \end{array} $ | (4) |
| $ \begin{array}{l} {{{G}}_y} = [{{g}}(x - 1,y - 1) - g(x - 1,y + 1)]\\ \;\;\;\;\;\;\;\;\; + 2 \times [g(x,y - 1) - g(x,y + 1)]\\ \;\;\;\;\;\;\;\;\; + [g(x + 1,y - {\rm{1}}){{ - g}}(x + 1,y + 1)] \end{array} $ | (5) |
图像的每一个像素的梯度的大小可由以下公式计算.
| $ {{G}} = \sqrt {{G_x}^2 + {G_y}^2} $ | (6) |
如果梯度值G或者G2大于某一阈值则认为该点属于边缘点.
2.2 sobel边缘检测算法处理仿真系统的搭建基于System Generator的Sobel边缘检测算法仿真系统模型如图1所示.
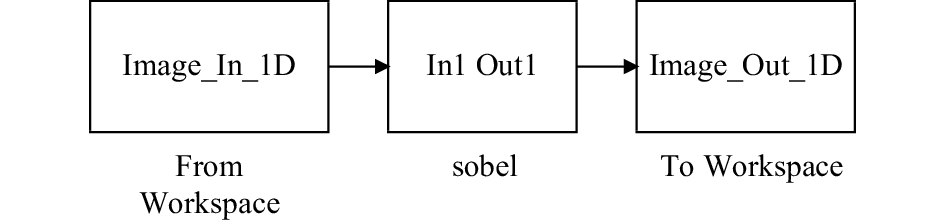
|
图 1 Sobel边缘检测算法仿真系统模型 |
数据源模块(Image_In_1D)是图像数据的输入模块, 通过调用Simulink中Souce目录下的From Workspace模块并加载Matlab程序来实现, 其功能是读入图像并将二维矩阵数据转化一维数据作为系统的数据源输入.
图像显示模块(Image_out)是图像数据的输出模块, 通过调用Simulink中Souce目录下的To Workspace模块并加载Matlab程序来实现, 用于把算法模块输出的一维数据流重新组合为二维矩阵并显示为图像.
2.3 Sobel边缘检测算法处理模块设计Sobel边缘检测模块的处理模型如图2: 图像数据经过三行缓存后同时通过X方向和Y方向两个滤波器, 在这两个滤波器中完成卷积运算, 对二者的运算结果平方后求和, 再经过阈值判断变为二值图像.

|
图 2 Sobel边缘检测模块的处理模型 |
图2中3LineBuffer子模块的功能是缓存三行图像数据并同时输出, 这个过程通过调用双口RAM资源来实现, 将一块RAM资源分成大小相等的两部分, 低地址部分实现一行缓存, 其输出经过高地址部分实现第二行缓存, 如图3.
XSobelFilter子系统如图4, 该子模块实现的功能是计算式(4), 其中, 滤波系统的2倍运算是通过移位来实现的, 系统中T, T1, T2的作用是屏蔽掉悬空引脚的报错信息. YSobelFilter设计结构与之类似.
其中, 两个滤波系统的2倍运算是通过移位来实现的. 阈值判决子系统如图5, 该子模块实现的功能是根据预设的阈值将图像二值化.
3 实验分析对系统进行在线仿真得到原图和边缘检测后的处理效果图, 由图6与图7, 可见系统较好地完成了边缘检测的任务.
将System Generator的设计结果编译为硬件描述语言并在ISE软件上建立工程, 进行综合得到RTL级视图. 对比图8的RTL级视图和图2的Sobel边缘检测模块的处理模型, 可以发现基于Syetem Generator的设计结果与ISE软件的综合结果在结构上是完全一样的, 从而进一步证明了设计的正确性.
基于Matlab环境仿真Sobel边缘检测算法可知: 对一副300×246的图像执行一次Sobel边缘检测大约耗时0.007 206 s. 而使用该算法模块完成一次运算需要约74 100(300×246+300)个时钟周期, 如果以50 M的时钟作为驱动, 耗时约0.001 482 s, 即每秒可处理约674帧图片, 处理速度提高了约7倍.
以Spartan6系列csg324型号FPGA内部拥有的资源情况为基准, 考察该设计资源消耗情况可以发现: 该算法模块消耗较少的资源, 这为后续实现更为复杂的算法留下了很大的空间.

|
图 3 三线缓存模块 |

|
图 4 X方向Sobel滤波计算模块 |
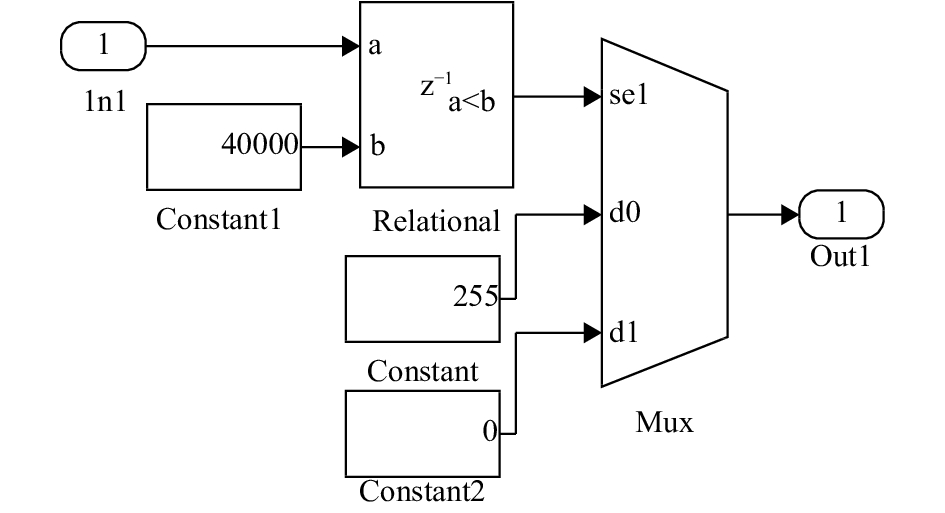
|
图 5 阈值判断模块 |
4 总结
本文在Matlab/Simulink平台上实现了基于System Generator的Sobel边缘检测算法的图形化建模. 实现了对该算法的在线仿真并将设计结果编译为硬件描述语言(HDL). 相比传统的基于HDL语言的设计方案, 在实现同样功能的前提下, 本设计极大的缩短了开发周期并支持在线查看图像处理结果. 文章最后还对算法模块的设计结果进行了分析, 讨论了图像的直观处理结果、RTL级视图、实际消耗资源以及运行速度等情况.

|
图 6 处理前图像 |

|
图 7 处理后图像 |
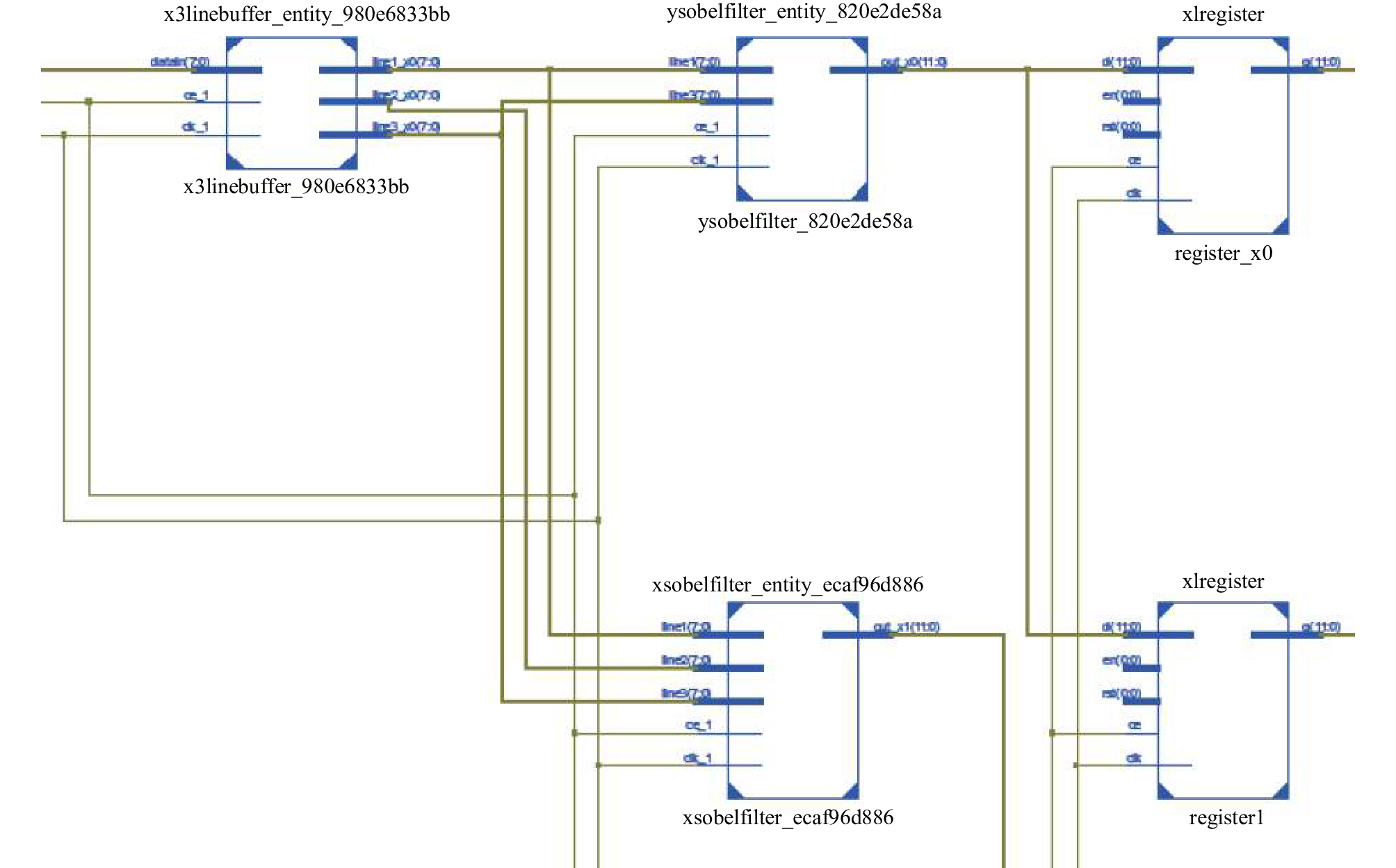
|
图 8 RTL级视图 |
| 表 1 资源使用情况表 |
| [1] |
覃永新, 田玉晓, 陈文辉. 图像边缘检测器的FPGA实现. 广西科技大学学报, 2017, 28(3): 88-91, 109. |
| [2] |
胡红伟. 基于FPGA的图像边缘检测系统研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [3] |
张伟. 基于FPGA的车牌识别中值滤波算法的研究与实现[硕士学位论文]. 天津: 天津大学, 2014.
|
| [4] |
Wang SY, Wang X. Realization of edge detection algorithm based on FPGA by simulink. Computer Systems & Applications, 2016, 25(5): 89-93. |
| [5] |
Liu BF, Gao LP. Sobel image edge detection method based on FPGA. Applied Science and Technology, 2016, 43(6): 59-61. |
| [6] |
Du ZC, Ning LF. Image edge detection based on Sobel algorithm in FPGA implementation. Application of Electronic Technique, 2016, 42(10): 89-91, 95. |
| [7] |
王博. 基于FPGA的视频信号处理的应用[硕士学位论文]. 济南: 山东大学, 2016.
|
| [8] |
高静. 基于LabVIEW图形化编程的PID控制算法. 软件导刊, 2012, 11(4): 51-53. |
| [9] |
Ma T, Chen J, Shan H. FPGA design of digital down converter based on DSPBuilder. Application of Electronic Technique, 2006, 32(7): 93-96. |
| [10] |
郭俊位. USDR平台中FPGA图形化设计关键技术研究[硕士学位论文]. 成都: 电子科技大学, 2013.
|
| [11] |
Zhang Q, Jia FX, Yin TT. Design of real-time image edge detection system based on improved Sobel algorithm. Instrument Technique and Sensor, 2018(2): 101-104, 108. |
| [12] |
李丹阳. 基于Soble算子的图像边缘检测优化设计. 数字技术与应用, 2017(11): 137-138. |
| [13] |
黎天赐. 一种阈值自适应的边缘检测算法及其FPGA实现[硕士学位论文]. 广州: 华南理工大学, 2016.
|
| [14] |
刘开健. 基于FPGA的实时图像处理系统的设计与实现[硕士学位论文]. 昆明: 昆明理工大学, 2008.
|
| [15] |
乔磊. 基于FPGA的图像边缘检测系统研究与设计[硕士学位论文]. 淮南: 安徽理工大学, 2017.
|
| [16] |
Gan JW, Qin FJ, Cao B. Design of FPGA image processing system for the bubble edge detection. Journal of Chinese Agricultural Mechanization, 2015, 36(2): 293-296. |
| [17] |
Liu J, Yang S, Yu HM. Improvement and realization of Sobel algorithm in license plate recognition system. Computer Systems & Applications, 2010, 19(5): 209-211. |
| [18] |
吴天明, 赵新力, 刘建存. MATLAB电力系统设计与分析. 2版. 北京: 国防工业出版社, 2007. 28–46.
|
 2019, Vol. 28
2019, Vol. 28



