2. 聚光科技(杭州)股份有限公司, 杭州 310052
2. Focused Photonics (Hangzhou) Inc., Hangzhou 310052, China
地表水是人类用水的重要来源之一, 人类每天生活用的自来水就是地表水经过加工后提供的, 由于工业废水排放和人为生活废水乱排等原因, 导致地表水污染严重, 水体中的氮、磷等元素含量增加, 水污染问题已经严重破坏了生态环境[1]. 为了有效的进行地表水水质管理和保护, 目前很多专家和学者积极进行水质污染防控的研究, 同时也迫切需要对地表水监测因子进行分析预测, 以便提供多方面的管理决策.
目前常用水质监测因子的预测方法有人工神经网络、深度循环神经网络、灰色预测模型等等, 吴旭东、李映曦等[2]人利用基于径向基的RBF神经网络算法建立水质评价预测模型, 实验结果预测准确率较高; 杨祎玥等[3]人利用深度循环神经网络的时间序列预测模型结合小波变换方法, 采用时间进化反向传播算法(BPTT), 更新网络权值进行训练, 减少了水文序列预测的滞后; 张青、袁宏林等[4,5]人建立BP神经网络水质预测模型对水质相关指标进行预测, 取得了良好的效果; 李宣谕等[6]人利用动态灰色可修正模型以一定的权重对不同预测模型的预测值加权进行水质预测, 得到了较好的结果; 这些算法虽然各有优点, 但是在输入数据的噪音处理以及算法模型对时间序列的数据分析上还有欠缺, LSTM神经网络具有选择记忆的特点, 任君等[7]人用LSTM做了关于股票指数预测的研究, 得到了良好的结果, 通过查找相关文献发现利用LSTM对地表水水质的预测鲜有报道, 因此, 提出了一种基于K-Similarity降噪的LSTM神经网络水质多因子预测方法, 本算法能够降低数据噪声, 提高预测准确度. 在相同的条件下, 利用某站点地表水水质监测数据进行仿真对比实验, 证实了所提出预测模型的优越性.
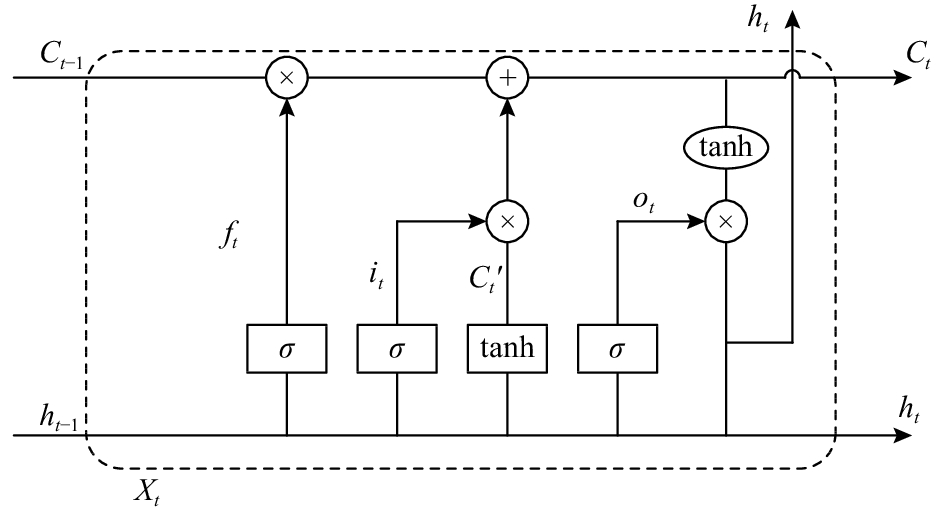
1 LSTM算法原理长短期记忆[8,9](Long Short-Term Memory neural network, LSTM)是一种特殊形式的递归神经网络(Recurrent Neural Networks, RNN), 它的选择性记忆功能和其单元内部的门控(输入门、输出门、遗忘门)结构改进了递归神经网络, 其基本思想是神经元受控于多个门控, 以此来克服神经网络中的梯度消失, 能够深入挖掘时间序列中的固有规律. LSTM神经网络的每个细胞有三个门控, 输入门(Input gate)、遗忘门(Forget gate)和输出门(Output gate), 其模块结构如图1所示, 圆圈表示逐点运算, 矩形表示神经网络层.
|
图 1 LSTM门控模块结构图 |
设
| ${i_t} = \sigma ({W_{xi}}{x_t} + {W_{hi}}{h_{t - 1}} + {W_{ci}}{C_{t - 1}} + {b_i})$ | (1) |
| ${f_t} = \sigma ({W_{xf}}{x_t} + {W_{hf}}{h_{t - 1}} + {W_{cf}}{C_{t - 1}} + {b_f})$ | (2) |
| ${o_t} = \sigma ({W_{xo}}{x_t} + {W_{ho}}{h_{t - 1}} + {W_{co}}{C_t} + {b_o})$ | (3) |
| $\sigma (x) = \frac{1}{{1 + {e^{ - x}}}}$ | (4) |
其中,
| $C_t' = \tanh ({W_{xc}}{x_t} + {W_{hc}}{h_{t - 1}} + {b_c})$ | (5) |
| ${C_t} = {f_t}{C_{t - 1}} + {i_t}C_t'$ | (6) |
| $\tanh (x) = \frac{{1 - {e^{ - 2x}}}}{{1 + {e^{ - 2x}}}}$ | (7) |
其中,
设有n(n>0)维输入
| ${y_t} = {o_t}\tanh ({C_t})$ | (8) |
本文以某站点的地表水水质监测数据为研究对象, 由于有多种因子对水质有影响, 因此在预测水质中的某一因子时, 其他的因子对其含量的变化影响也不容小觑, 因此采用LSTM构建水质多因子预测模型.
所谓的多因子预测, 是指在同一时刻的水质中含有的多种监测因子的指标数据是受其他因子相互作用和影响的, 利用多个因子的相互作用来共同预测下一时刻的某一因子的指标数据. 把每个因子的数值当做高维空间对应坐标轴中的坐标, 多个因子共同组成高维空间中的向量.
根据地表水环境质量标准以及水质因子相互影响的因素, 最终选取水温(x1)、PH(x2)、氨氮(x3)、总磷(x4)、高锰酸盐指数(x5)、溶解氧(x6)、总铅(x7)、电导率(x8)共8个指标作为模型输入参数, 同时, 将这8个指标作为输出参数水温(y1)、PH(y2)、氨氮(y3)、总磷(y4)、高锰酸盐指数(y5)、溶解氧(y6)、总铅(y7)、电导率(y8). 从某地表水水质监测站点采集2017年10月12日到2018年3月1日地表水水质监测因子相关数据, 采集时间周期为4个小时采样一次, 所选择数据样本部分数据如表1所示.
| 表 1 部分样本数据信息表 |
2.2 数据预处理
由于监测站点采集的数据因子指标范围较大, 数据参差不齐, 并且数据样本由八个不同指标组成, 这些指标具有不同的量纲和量级. 为了保证时间序列数据趋于稳定以及模型的高效性, 首先对数据进行归一化处理, 将其转换到[0, 1]之间. 本文采用最大值最小值归一化方法进行处理, 公式如式(9):
| $x_t' = ({x_t} - {x_{\min }})/({x_{\max }} - {x_{\min }})$ | (9) |
公式中
K-Similarity降噪法是本文提出的一种应用于高维空间向量簇中判别噪声的方法, 它是通过将N个数据对象划分为K个类簇, K的意义类似于K-Means算法[10,11]中的聚类数目; 在每个类簇中将向量余弦相似度[12,13](即Similarity)作为噪声判别指标去除噪声. 若输入类簇数目为K、数据对象为N则具体流程如下:
(1) 将样本中数据划分为K个类簇, 计算每个类簇的质心[14](即重心向量, 是衡量向量簇中的向量偏离度或相似度的重要指标)作为类簇中心.
(2) 对每个类簇, 计算类簇内各向量到其质心的余弦相似度.
(3) 根据向量余弦相似度的大小来判别噪声.
通过参考相关文献资料[15,16]发现, 近似简谐波变化规律的数据在降噪过程中能更容易的将偏差过大的向量分辨出来, 本文所选用的地表水水质监测数据也呈现出随着时间有近似周期变化的规律. 因此利用本文提出的K-Similarity降噪法对LSTM预测模型的输入数据进行降噪.
设LSTM中N个样本数据按照时间
为了使降噪更加高效稳定, 首先将输入向量进行单元化(将原有的高维空间向量长度归一), 然后再计算向量簇的质心, 计算公式如式(10)和式(11),
| $\overrightarrow X = (\frac{{{x_1}}}{{\sqrt {\sum\nolimits_1^n {x_i^2} } }},\frac{{{x_2}}}{{\sqrt {\sum\nolimits_1^n {x_i^2} } }},\cdots,\frac{{{x_n}}}{{\sqrt {\sum\nolimits_1^n {x_i^2} } }})$ | (10) |
| $\overrightarrow \mu = \frac{{\sum\nolimits_1^n {\overrightarrow {{A_i}} } }}{n}$ | (11) |
数据中的噪声向量往往与相邻或者相近的数据呈现较大差异, 在高维空间中主要体现在噪声向量与重心向量之间的夹角差距远远大于其他多数非噪声向量与重心向量之间的夹角的差距. 若两个向量的交角越小, 余弦值就越大, 两个向量也就越相似. 余弦相似度计算公式如式(12), 其中
| $similarity = \cos ine(\theta ) = \frac{{\sum\nolimits_1^n {({a_i} \times {b_i})} }}{{\sqrt {\sum\nolimits_1^n {a_i^2} } \times \sqrt {\sum\nolimits_1^n {b_i^2} } }}$ | (12) |
利用K-Similarity法降噪的具体步骤如下:
(1) 确定类簇数目K, 计算类簇质心
(2) 对于每个向量簇, 按照1)-3)进行计算.
1) 根据公式(12)计算簇内各对象到其质心的余弦相似度(即降噪有效性指标).
2) 按照余弦相似度升序排序, 计算最小值
3) 人工设定一个阈值
| $\mathop B\limits^ \to = \frac{{\mathop A\limits^ \to + \mathop C\limits^ \to }}{2}$ | (13) |
(3) 当所有数据类簇完成降噪即去除每个类簇中最大的噪声向量时结束.
2.4 K-Similarity降噪的LSTM水质多因子预测模型流程K-Similarity降噪的LSTM水质多因子预测模型主要可分为三步:
(1) 数据采集预处理部分, 首先对大量数据样本进行整合处理, 将无用数据和缺失数据删除, 按照时间先后进行排列作为实验的有效数据进行分析.
(2) K-Similarity降噪部分, 见上一节.
(3) LSTM算法部分, 通过降噪后的训练数据进行模型训练, 选择Adam算法[17]进行优化, 设置学习率来更新权重减少损失, 最后使用测试集数据进行验证. 模型流程图如图2所示.
本文选取均方误差MSE(Mean Squared Error)来评价预测性能, 均方误差是指参数估计与参数真值之差平方的期望值, 计算公式如(14)所示,
| $MSE = \frac{1}{N}\sum\nolimits_{t = 1}^N {{{({y_t} - {p_t})}^2}} $ | (14) |

|
图 2 模型流程图 |
3 实验结果分析
实验平台和环境: 实验所使用计算机配置如下: 处理器为2.3 GHz Intel Core i5, 内存为8 GB, 操作系统为macOS High Sierra 10.13.2; 程序设计语言为Python2.7.10; 集成开发环境为Pycharm Professional 2016.2.3; 程序中TensorFlow由1.6.0版本实现、scikit-learn由0.19.1版本实现. 实验相关参与设置: LSTM时间步长time_step为20, 隐层单元数为10, 批量大小batch_size为60, 学习率为0.001. 针对获取的783个数据样本, 将前743个作为模型训练数据, 后40个作为模型验证数据, 进行预测.
为了验证本文提出的预测模型的有效性, 选取BP神经网络、RNN、传统的LSTM神经网络等预测模型进行对比实验. 四个预测模型均在相同的实验平台和环境下进行实验, 对于BP神经网络采用三层神经网络, 11个隐层单元, 学习率为0.001; 对于RNN采用10个隐层单元, 学习率为0.001, 时间周期为20, 激活函数采用relu函数; 对于本文K-Similarity降噪的LSTM和传统的LSTM均采用Adam随机梯度下降算法进行优化, 损失函数使用均方误差MSE进行评价. 为了消除一次实验结果的偶然性, 对每种算法模型进行50次实验, 计算出相应的误差. 实验对每个模型均进行了100次迭代, 并且在每次迭代完成后计算其均方误差, 并绘制出误差对比结果图, 如图3所示. 从图3中可以看出, 四种模型随迭代次数均方误差的变化情况, 本文通过K-Similarity降噪的LSTM神经网络模型与BP神经网络、RNN和传统的LSTM神经网络模型相比误差明显降低.

|
图 3 误差对比结果图 |
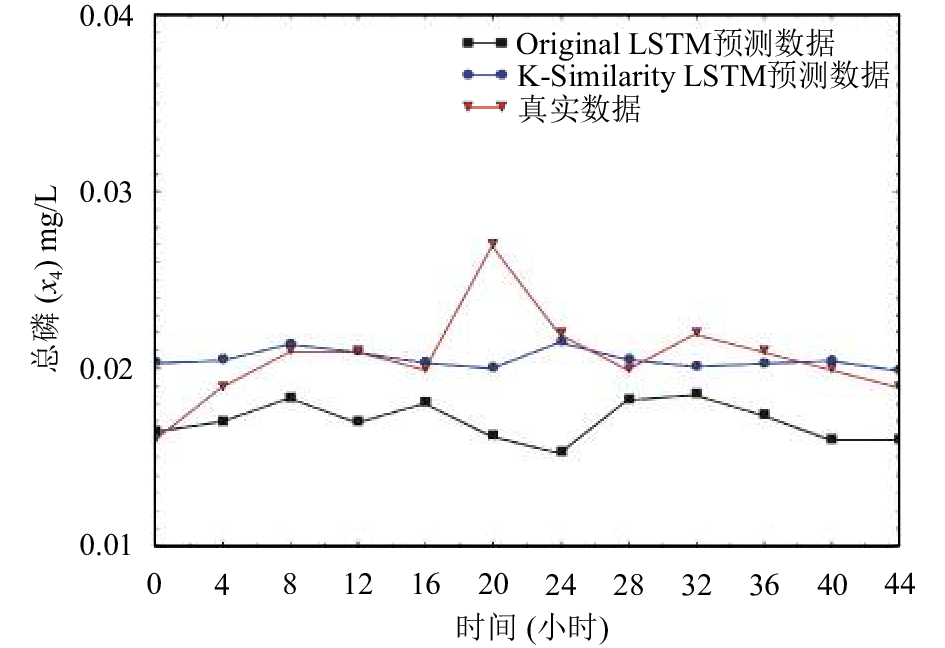
为了更加直观的看出K-Similarity降噪后的算法在预测效率上的提高, 以及模型对于每个因子的预测效果, 分别选取测试集的12个数据, 绘制八个因子的实际数据与预测数据对比图, 如图4至图11. 从图中可以看出, 降噪后的算法模型的预测结果曲线和实际数值更加吻合, 与实际情况更加符合, 预测结果更加准确.

|
图 4 水温(x1)预测结果图 |

|
图 5 PH(x2)预测结果图 |

|
图 6 氨氮(x3)预测结果图 |
|
图 7 总磷(x4)预测结果图 |
根据测试集数据计算每个因子的平均相对误差E, 计算公式如式(15)所示.
| $E = \frac{{\sum\nolimits_{t = 1}^N {|({y_t} - {p_t})/{y_t}|} }}{N} \times 100\% $ | (15) |
每个因子的平均相对误差计算结果如表2所示, 从表中可知, 本文提出的算法预测模型平均相对误差相比于传统的LSTM模型大大降低. 水温平均相对误差比之前降低了51.4%, PH平均相对误差比之前降低了64.1%, 氨氮平均相对误差比之前降低了65.3%, 总磷平均相对误差比之前降低了55.9%, 高锰酸盐指数平均相对误差比之前降低了79.4%, 溶解氧平均相对误差比之前降低了44.9%, 总铅平均相对误差比之前降低了84.5%, 电导率平均相对误差比之前降低了84.2%.

|
图 8 高锰酸盐指数(x5)预测结果图 |
|
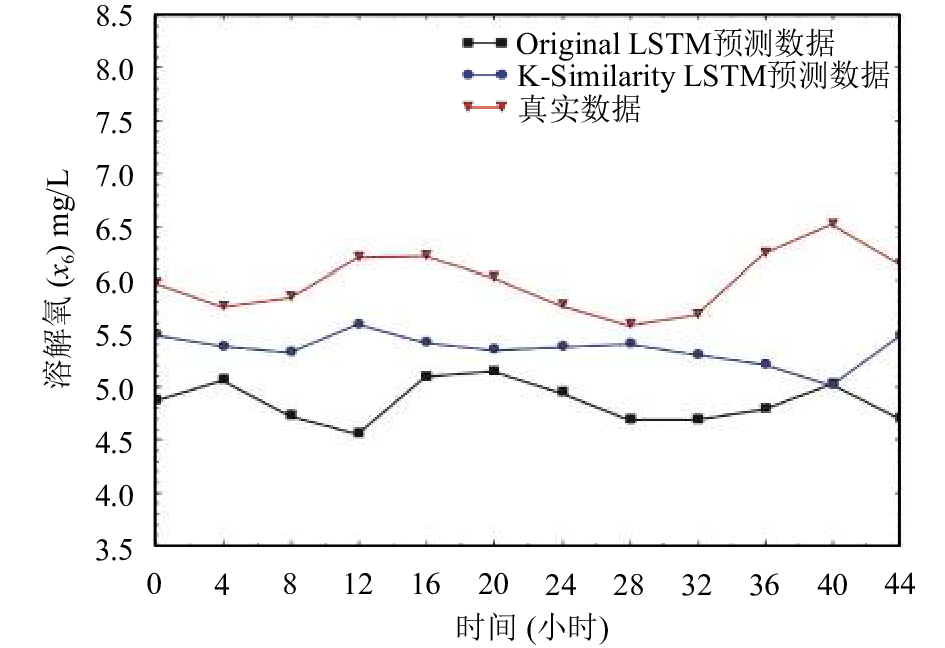
图 9 溶解氧(x6)预测结果图 |

|
图 10 总铅(x7)预测结果图 |
|
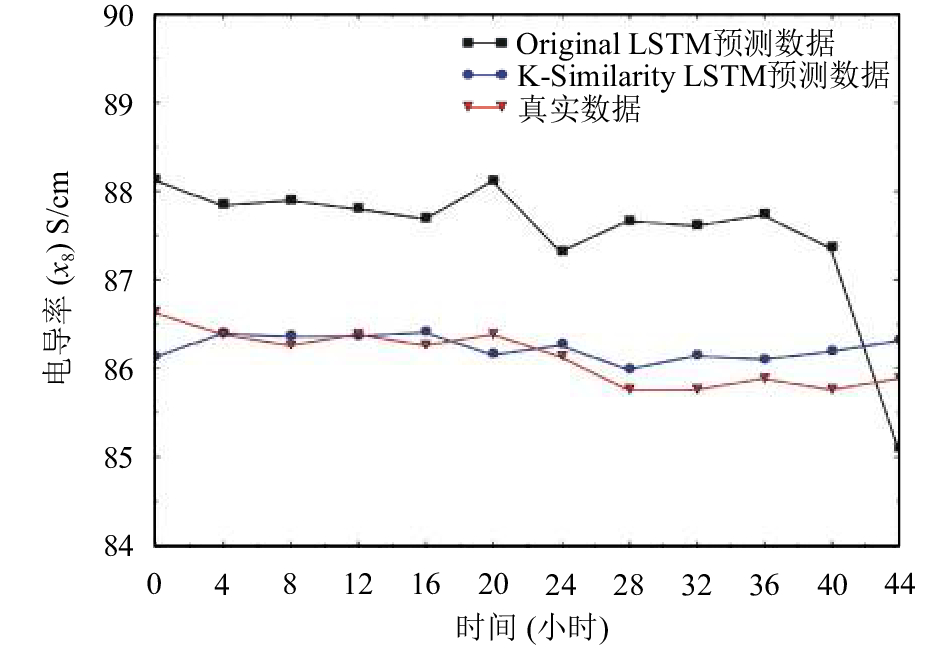
图 11 电导率(x8)预测结果图 |
从以上实验结果可知, 本文提出的预测模型均方误差最小, 并且每个预测因子的平均相对误差均明显降低, 预测结果更加准确. 因此本文提出的模型可以应用到地表水水质因子预测中, 为地表水水质预测提供参考.
| 表 2 预测因子平均相对误差表(%) |
4 结论
本文首先针对地表水水质预测的多因子影响因素建立高维空间坐标体系, 利用最大值最小值归一化方法对监测站点水质因子数据进行数据预处理, 简化了数据的波动和复杂性, 然后将K-Similarity降噪法与LSTM算法结合, 通过计算高维空间中向量的余弦相似度来去除噪声, 最后进行训练和预测. 实验结果表明: 本文提出的预测模型的均方误差最小, 预测结果曲线与实际数据更加吻合, 平均相对误差明显降低, 预测结果比BP神经网络、RNN和传统的LSTM神经网络模型更优, 模型预测更加准确. 在地表水水质多因子预测方面能够取得较好的效果, 对于水质预测具有重要的实践意义. 基于目前的研究, 后续的主要研究工作是寻求更有效的参数优化方法.
| [1] |
刘冠凤. 聊城市地表水环境问题及对策研究[博士学位论文]. 武汉: 武汉理工大学, 2012.
|
| [2] |
吴旭东, 冯璐远, 陈正军, 等. 数据挖掘算法在水质评价预测中的应用. 电脑知识与技术, 2017, 13(35): 3-4, 12. |
| [3] |
杨祎玥, 伏潜, 万定生. 基于深度循环神经网络的时间序列预测模型. 计算机技术与发展, 2017, 27(3): 35-38, 43. |
| [4] |
张青, 王学雷, 张婷, 等. 基于BP神经网络的洪湖水质指标预测研究. 湿地科学, 2016, 14(2): 212-218. |
| [5] |
袁宏林, 龚令, 张琼华, 等. 基于BP神经网络的皂河水质预测方法. 安全与环境学报, 2013, 13(2): 106-110. DOI:10.3969/j.issn.1009-6094.2013.02.023 |
| [6] |
李宣谕. 基于人工智能对地表水的水质预测与评价研究[硕士学位论文]. 吉林: 东北电力大学, 2017.
|
| [7] |
任君, 王建华, 王传美, 等. 基于正则化LSTM模型的股票指数预测. 计算机应用与软件, 2018, 35(4): 44-48, 108. DOI:10.3969/j.issn.1000-386x.2018.04.008 |
| [8] |
Li X, Peng L, Yao XJ, et al. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environmental Pollution, 2017, 231: 997-1004. DOI:10.1016/j.envpol.2017.08.114 |
| [9] |
Fischer T, Krauss C. Deep learning with long short-term memory networks for financial market predictions. European Journal of Operational Research, 2018, 270(2): 654-669. DOI:10.1016/j.ejor.2017.11.054 |
| [10] |
李卫军. K-means聚类算法的研究综述. 现代计算机, 2014(23): 31-32, 36. |
| [11] |
周爱武, 于亚飞. K-Means聚类算法的研究. 计算机技术与发展, 2011, 21(2): 62-65. DOI:10.3969/j.issn.1673-629X.2011.02.016 |
| [12] |
谢平, 肖婵, 雷红富, 等. 基于向量相似度原理的湖泊富营养化评价方法及其验证. 安全与环境学报, 2008, 8(4): 93-96. DOI:10.3969/j.issn.1009-6094.2008.04.024 |
| [13] |
陈春芳, 朱传喜. 基于向量相似度的区间数排序方法及其应用. 统计与决策, 2014(3): 76-78. |
| [14] |
谢华, 王健, 林鸿飞, 等. 基于特征选择的质心向量构建方法. 计算机工程, 2012, 38(1): 195-196, 210. DOI:10.3969/j.issn.1000-3428.2012.01.062 |
| [15] |
孙红星, 张洋. 改进阈值函数在振动信号降噪中的仿真研究. 系统仿真学报, 2017, 29(8): 1788-1794. |
| [16] |
赵化彬, 张志杰. 基于本征模态函数最优配比的冲击波信号经验模态分解降噪方法. 科学技术与工程, 2017, 17(18): 231-237. DOI:10.3969/j.issn.1671-1815.2017.18.036 |
| [17] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv: 1412.6980, 2014.
|
 2019, Vol. 28
2019, Vol. 28



