2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
计算流体力学方法将连续的物理空间离散为网格单元构成的计算空间, 通过对流体控制方程(Navier-Stokes方程)的离散求解达到揭示分析流动特性的目的. 计算网格从单元形状和数据结构上可分为结构化网格、非结构化网格和笛卡尔网格等[1]. 结构网格的特点是拓扑结构有序, 逻辑关系简单, 流场计算精度和效率高, 缺点是对复杂外型的适应性差, 在确定各种复杂外型的空间拓扑关系时显得非常困难, 难以自动化生成, 从而需要投入大量人工时间. Steger[2,3]提出了“重叠网格”的概念, 将流场模拟区域分解为若干子区域, 在每个子区域上分别生成高质量网格, 各个子区域之间存在相互重叠关系. 在流场计算过程中, 通过重叠网格内各套子网格之间的插值实现流场信息传递, 这样对于复杂的外型结构, 不同的外型区域可以单独生成拓扑, 不用再进行耗时的复杂拓扑划分, 弥补了结构网格的缺点, 同时保持了结构化网格计算精度高和边界处理能力强的优点, 扩展了对复杂外型和运动问题的适应性, 减少了生成网格的时间和工作量, 因而得到了较广泛的应用.
重叠网格的实现过程分为挖洞、找点和插值3个步骤[4], 即首先确定并标记出流场计算中无意义的重叠网格单元、然后确定各个网格点在其他网格中的位置对应关系和相应的插值贡献单元, 最后在重叠边界处通过贡献单元向插值点传递流场信息, 实现整个流场的同步更新. 为了减少重叠网格处理的迭代时间, 通常采用阵面推进类方法确定洞边界和进行洞面优化[5], 此类方法对网格点数据的连续性要求高, 不利于并行扩展和应用, 尤其对于网格量大的复杂外型流场模拟. YikLoon Lee[6,7]提出了结构网格的隐式挖洞算法, 相比于阵面推进类方法, 隐式挖洞算法采用网格密度严格对比的找点过程, 替换传统重叠网格方法的网格状态标识和贡献单元寻址步骤, 保留流场信息插值这一环节, 其最大特点是不需要额外的重叠关系输入文件, 重叠网格切割和贡献单元寻址在一个过程中同时完成. Landmann B[8]对隐式挖洞的流程进行了并行化实现, 分析了网格装配各个阶段的耗时对比以及算法并行扩展性. Kenway GK[9]等对隐式重叠方法的并行特性进行了较为细致的研究, 根据不同网格块之间的重叠关系, 建立“重叠矩阵”, 将网格比较分配到不同进程进行, 并根据重叠网格区域大小、实际的查找耗时对网格的分配进行优化, 达到数千核的并行扩展效果, 并指出了隐式挖洞方法负载不均衡的局限性.
隐式挖洞算法中网格之间的比较判断会占用大量时间开销, 对于工程实际的复杂构型, 网格重叠的结果可能是某些区域的子网格块需要和所重叠的其他子网格中大量网格块进行信息交换. 因此在并行算法设计中, 需要综合考虑网格挖洞插值和计算阶段的负载平衡, 并尽量减少全局通信. 本文在并行隐式挖洞算法实现的基础上, 提出了笛卡尔辅助网格和多块结构网格的混合网格方法. 通过基于搭接边界的多层背景网格, 实现隐式挖洞的快速确定洞边界和网格间插值关系的快速建立; 通过对重叠区域网格重叠权重的定义和应用, 建立混合网格的并行分配模式和负载均衡模型, 有效减少重叠插值信息在各进程间的通信, 并实现计算负载和通信负载在各个进程的均匀分配.
1 并行混合重叠网格算法 1.1 并行隐式挖洞算法并行隐式挖洞算法的实现流程如图1所示, 将读入的多块结构网格分为背景网格和子区域网格2类: 背景网格包围主要部件, 覆盖从部件物面边界到远场的整个流场区域, 子区域网格包围其他部件, 从部件的物面边界法向向外延伸一定距离, 重叠在背景网格的区域之内. 将背景网格和子区域网格块分配到不同的节点. 在各个节点内, 根据网格质量的定义, 分别计算所分配网格点的网格单元体积和到壁面的最短距离, 作为网格质量的组成因素. 然后对每个网格单元进行初始化标记, 将所有的背景网格标记为计算, 将所有的子区域网格标记为插值.

|
图 1 并行隐式挖洞方法流程 |
之后在每个进程内计算各个子区域的坐标范围, 归约到主进程, 得到各个子区域的包围盒, 再将所有包围盒信息发送到各个节点. 后续仅需要考虑包围盒内的网格单元. 对于这些单元需要进行网格标记并寻找贡献单元, 在各个节点进行的网格质量比较, 如果子区域网格单元质量更高, 将其标记由改为计算, 所对应的背景网格单元标记为插值, 然后将更新后的网格属性标记收集并存储到主进程, 主进程得到所有更新后的网格信息. 用于下一阶段的流场计算.
网格密度的定义需要结合网格生成的特点, 包括网格单元的体积和网格距离物面边界的距离, 通常在物面附近, 网格具有较小的网格单元体积, 较好的正交性和合理的过度. 本文中采用网格体积和网格到壁面距离的组合作为网格密度的定义, 如式(1)所示:
| $ Q = 1/\left( {{v^a} \cdot {d^b}} \right) $ | (1) |
其中, v为网格单元的体积, d为网格距离物面边界的距离, 通过a和b参数的调节改变网格体积和网格距离物面距离两个因素的影响, 取a=1, b=0时仅考虑网格尺度作为网格质量, 取a=0, b=1时仅考虑网格到物面距离作为网格质量. 对网格体积的计算可以在各个网格单元所分配的进程内分别进行, 不需要与其他进程进行数据交换.
1.2 笛卡尔背景网格本文将笛卡尔辅助背景网格引入到重叠网格系统, 在多块结构网格的重叠网格中, 通常对模拟中主要部件或非定常过程中静止部件生成覆盖整个模拟区域的多块网格, 如多段翼型或机翼的主翼、飞行器挂载分离模拟中的飞行器、子母弹抛撒模拟中的母弹等; 对于运动部件或复杂的构件, 生成覆盖流场局部区域的子网格块, 构成重叠网格系统. 采用笛卡尔辅助网格后, 在物体物面到法向向外足够包含附面层区域的一定距离内, 各自生成贴体的局部网格作为输入文件, 流场中的其他范围由在预处理中生成的笛卡尔网格覆盖. 图2显示的是加入笛卡尔辅助网格后30P30N多段翼型模拟需要的网格输入, 即各自围绕主翼、襟翼和副翼, 在法向一定距离内生成的贴体曲面网格. 在预处理过程中生成覆盖从各个物面到远场模拟区域的笛卡尔网格作为辅助背景网格. 在靠近模拟物体附近的辅助笛卡尔网格中, 各个方向采用固定的网格间隔, 这样在背景网格某一区域内可以根据网格点的编号方便的确定出网格的体积, 即隐式挖洞中的网格密度(背景辅助网格中不存在物面边界, 不必考虑网格点到壁面的距离).
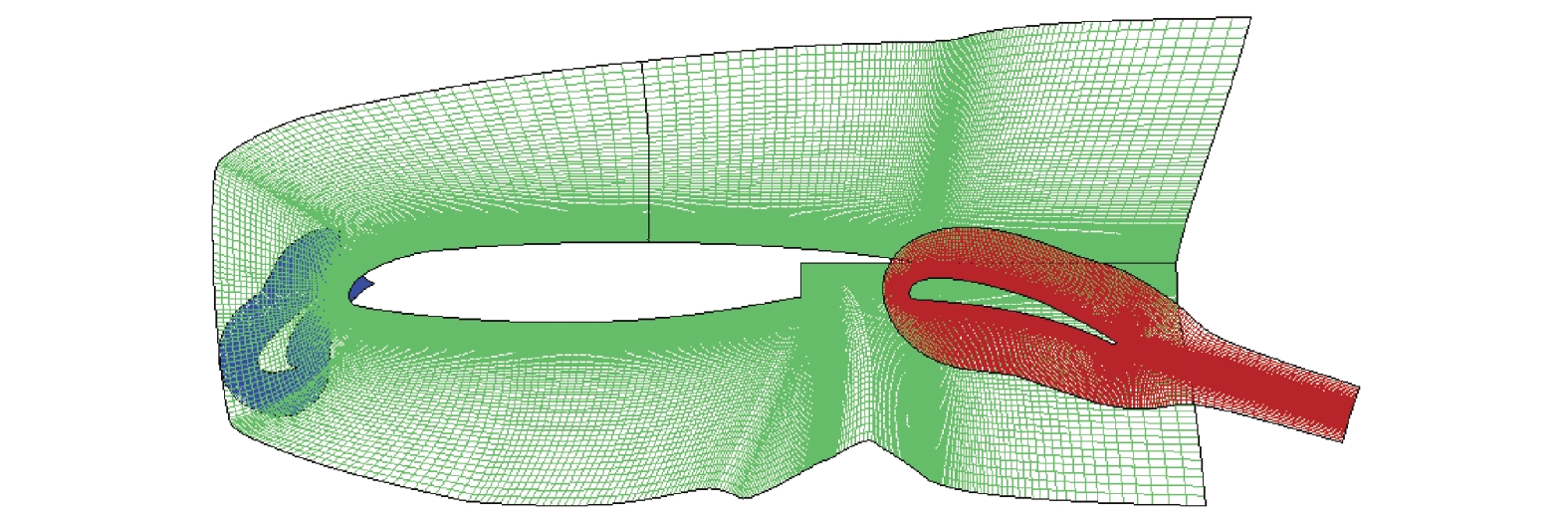
在预处理阶段中生成辅助笛卡尔网格需要确定辅助网格单元的尺寸和整个网格区域的大小, 两者均可以从输入的贴体网格中得到. 为了使重叠边界产生在远离固壁边界的的合适位置, 首先计算出子区域网单元尺寸的最小值和最大值, 再根据具体问题乘以合适的比例系数. 得到背景网格的单元尺寸. 通过计算各个模拟物体在各方向的长度, 在各个方向上扩大一定距离确定远场边界的位置. 生成的笛卡尔网格按规则结构网格的数据形式组织, 与各个部件网格在预处理阶段统一进行网格的分区, 并分配至各个进程, 图3展示的是执行隐式挖洞后的效果, 各段翼型与背景的重叠边界, 各段翼型之间的重叠边界均清晰的建立起来.
|
图 2 翼型附近区域的贴体网格 |

|
图 3 挖洞处理后的翼型网格和笛卡尔网格边界 |
1.3 基于笛卡尔网格域的找点插值方法
重叠网格找点的过程即是建立网格间插值关系的过程, 这一过程往往是重叠网格关系中耗时最多的步骤. 引入笛卡尔辅助背景网格后, 可以利用辅助网格数据结构简单, 网格单元标记和网格点坐标存在直接联系的特点, 通过背景网格寻找各个网格单元所要进行比较的单元, 也同时标记为插值的贡献单元, 在不同重叠子网格单元之间建立插值关系.
对近壁面区域背景网格采用相同的网格单元, 各方向网格单元的间隔是相等的, 即所有的网格单元具有相同的Δx, Δy和Δz, 因此可以建立网格数组标记和网格坐标的直接联系, 根据部件网格坐标确定背景网格数组值的步骤为: 对某一个部件网格单元, 首先根据辅助背景网格的分块边界, 确定网格单元位于哪一个背景网格块之内, 之后根据该网格单元格心的坐标与部件网格边界坐标各方向的差, 以及背景各个方向的单元大小, 确定出该部件网格单元在背景块内的编号. xo, yo, zo表示部件网格点(l, m, n)的坐标,xb, yb, zb 表示背景网格的坐标, Δx, Δy和Δz表示在各个方向上背景网格的单元间隔, 通过式(2), 即可以得到与该部件网格存在插值关系的背景网格单元的i, j, k编号.
| $\left\{ \begin{aligned} & i = \left\lfloor {\frac{{{x_o}({{l,m,n}}) - {x_b}(1,1,1)}}{{\Delta x}}} \right\rfloor \\ & j = \left\lfloor {\frac{{{y_o}({{l,m,n}}) - {y_b}(1,1,1)}}{{\Delta y}}} \right\rfloor \\ & k = \left\lfloor {\frac{{{z_o}({{l,m,n}}) - {z_b}(1,1,1)}}{{\Delta z}}} \right\rfloor \end{aligned}\right. $ | (2) |
定义网格块重叠权重系数的概念, 将所有的网格被分为2个部分, 对于不存在重叠关系的网格单元, 定义为背景区域, 其权重系数设置为1, 对于存在重叠关系的网格单元, 定义为混合区域, 如果有n套网格, 那么权重系数定义为n. 在将网格分配到各个进程时, 根据重叠关系将位于同一坐标区域内的网格尽可能分配到同一进程, 达到避免部分进程间插值信息通信的目的.
2 通信优化算法实现 2.1 网格块与背景辅助网格块的绑定在确立网格插值关系的流程之后, 每个部件块的网格单元均记录了相应的背景块中网格单元插值信息, 对各个部件网格块的信息进行遍历, 累加统计出每个部件网格块在各个背景网格块内插值点的数目. 比较得到与该部件网格块插值点最多的背景网格块, 即与附件网格块重叠区域最大的背景块, 遍历结束后, 每个部件网格块绑定唯一的一个背景网格块编号, 在后续分配到各个计算节点时, 将部件网格块与其绑定的背景网格块分配到同一个节点内, 如图4所示, 蓝色网格线表示部件贴体子网格的网格块, 红色网格线表示背景辅助网格的网格块, 部件网格块(1234)与背景网格多个网格块重叠, 根据重叠关系可分为(156)、(2567D9)、(738D)、(48D)和(94D) 5个部分, 根据网格块(1234)中各个单元记录的插值关系, 计算出与其重叠的五个背景网格块内重叠的点数, 比较得到网格点数最多的背景网格块, 如图所示为背景网格块(ABCD), 标记为部件网格块(1234)绑定的背景网格块, 在并行分配过程中分配到同一节点.

|
图 4 确定部件网格块绑定的背景网格块 |
在执行该流程的同时, 对于每一个背景网格块, 统计与其绑定的部件网格块数目, 作为该背景网格块分配的重叠权重系数, 并将该背景网格块标记为重叠块, 没有被标记的背景网格块为非重叠块. 在分配过程中, 重叠背景块与非重叠背景块分开处理, 对于重叠背景块, 其分配的节点预留其绑定部件块的空间, 将与其绑定的块分配在同一个进程.
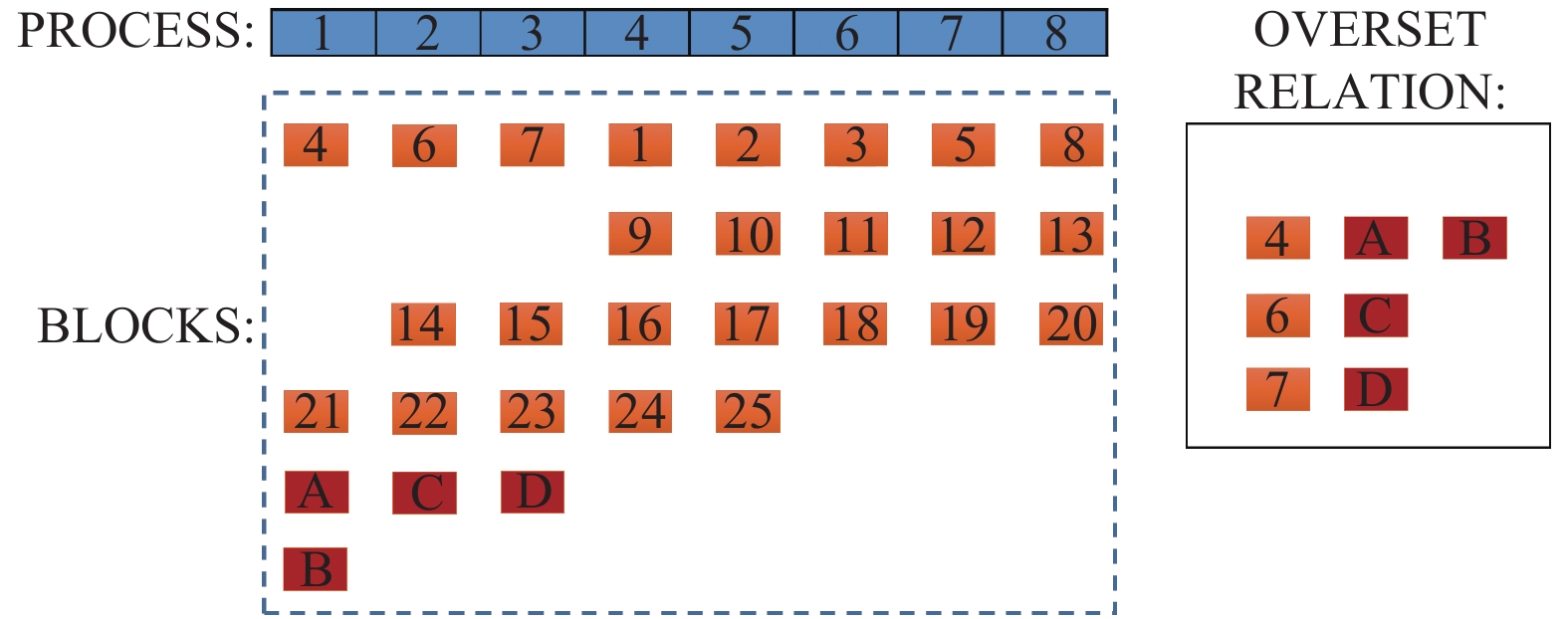
2.2 网格块的分配算法网格预处理分块后的块数达到数倍于计算分配的节点数, 实际分配中网格块会循环多次. 由于分块分配在预处理阶段进行, 所有网格块最终循环轮数是不确定的, 每个节点上最多分配的网格块数量也是无法预知的. 所以采取如下处理方法: 把重叠的背景块最先处理, 按照重叠权重降序进行排列, 第一次循环每个网格块都分配节点, 从第二次循环开始, 直到重叠系数为n的背景块循环到第n+1次之前, 跳过该背景网格块不分配, 以预留给绑定的部件网格块. 当所有背景网格块循环分配完毕后, 把各个部件网格块分配到所绑定的背景块所在节点.
以图5为例进行说明, 重叠网格系统中共有背景网格块25块, 部件网格块3块, 分配到8个进程. 背景网格中编号4、6、7的块与部件网格重叠, 第4块与部件网格块A和B重叠, 权重系数定义为3, 第6块和第7块分别与部件网格块C和D重叠, 权重系数定义为2. 在分配之前把有重叠关系的背景块按权重系数排在前面, 确保重叠的背景块先分配到进程号, 从第2次循环开始, 第4块轮空两次, 第6块和第7块轮空一次, 之后的非重叠块依次分配. 待所有背景网格块分配完后, 把部件网格块分配到相应的背景块所在节点.
|
图 5 根据重叠权重进行网格分配 |
3 算法测试与分析
为了验证本文提出混合重叠网格方法和通信优化方法的有效性. 选用ANF模型[10,11]对算法进行测试分析. ANF模型由锥头圆柱弹身和4个尖头弹翼组成, 弹体子网格的网格量为1039万, 每个弹翼网格子网格的网格量为52万, 在预处理过程中根据贴体网格信息, 生成多层背景网格, 组成总计3017万的重叠网格系统. 输入ANF模型的贴体网格拓扑如图6所示.

|
图 6 ANF贴体重叠网格拓扑结构 |
测试在中国科学院计算机网络信息中心的“元”高性能计算系统进行, 系统每个刀片节点配备两颗Intel Xeon E5-2680V3处理器(2.5 GHz, 12核), 256 GB内存. 编译环境为Intel Fortran+OpenMPI, 使用-O2编译优化选项. 分别使用64核、128核、256核、512核及1024核进行测试并分析.
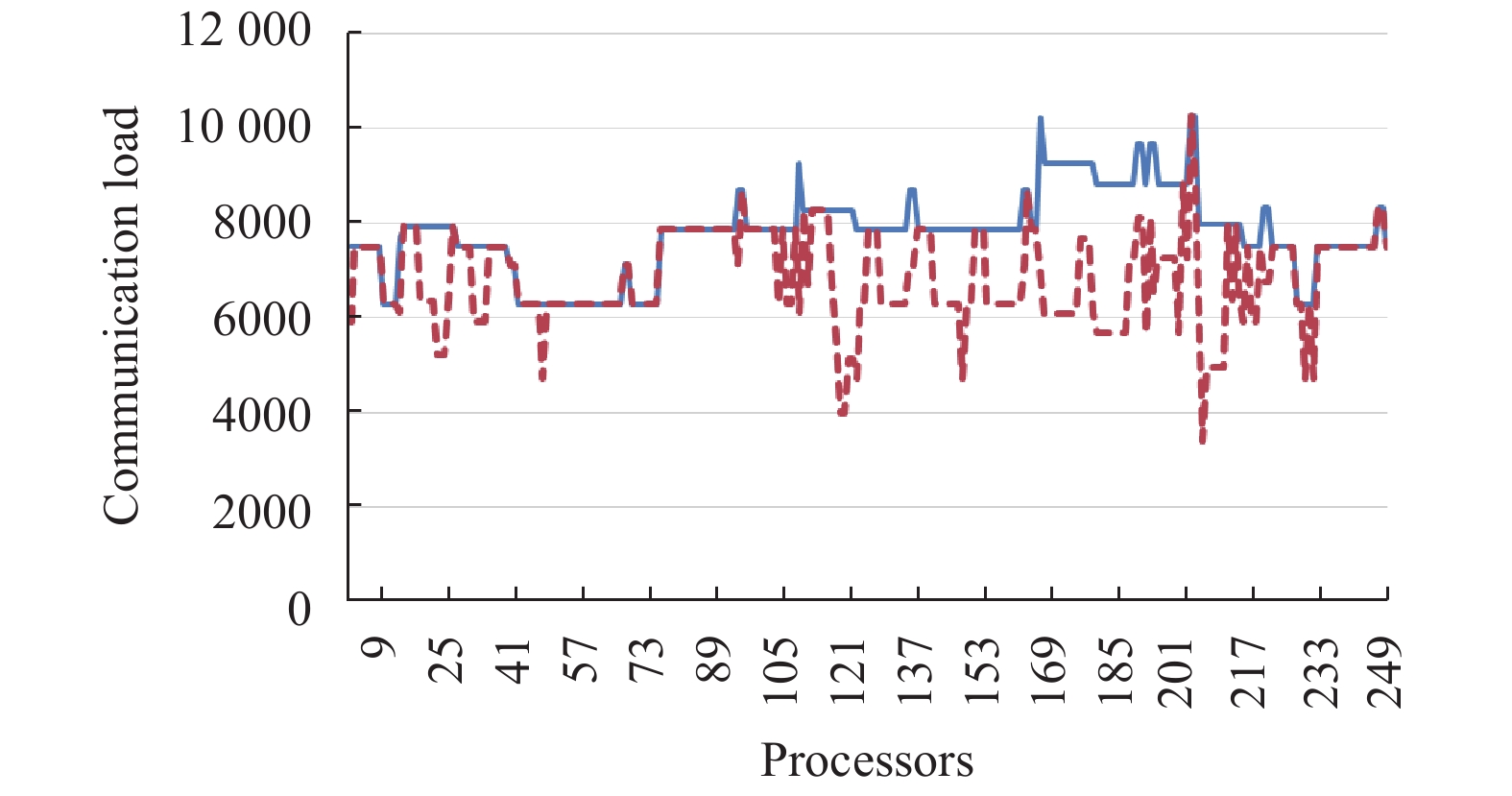
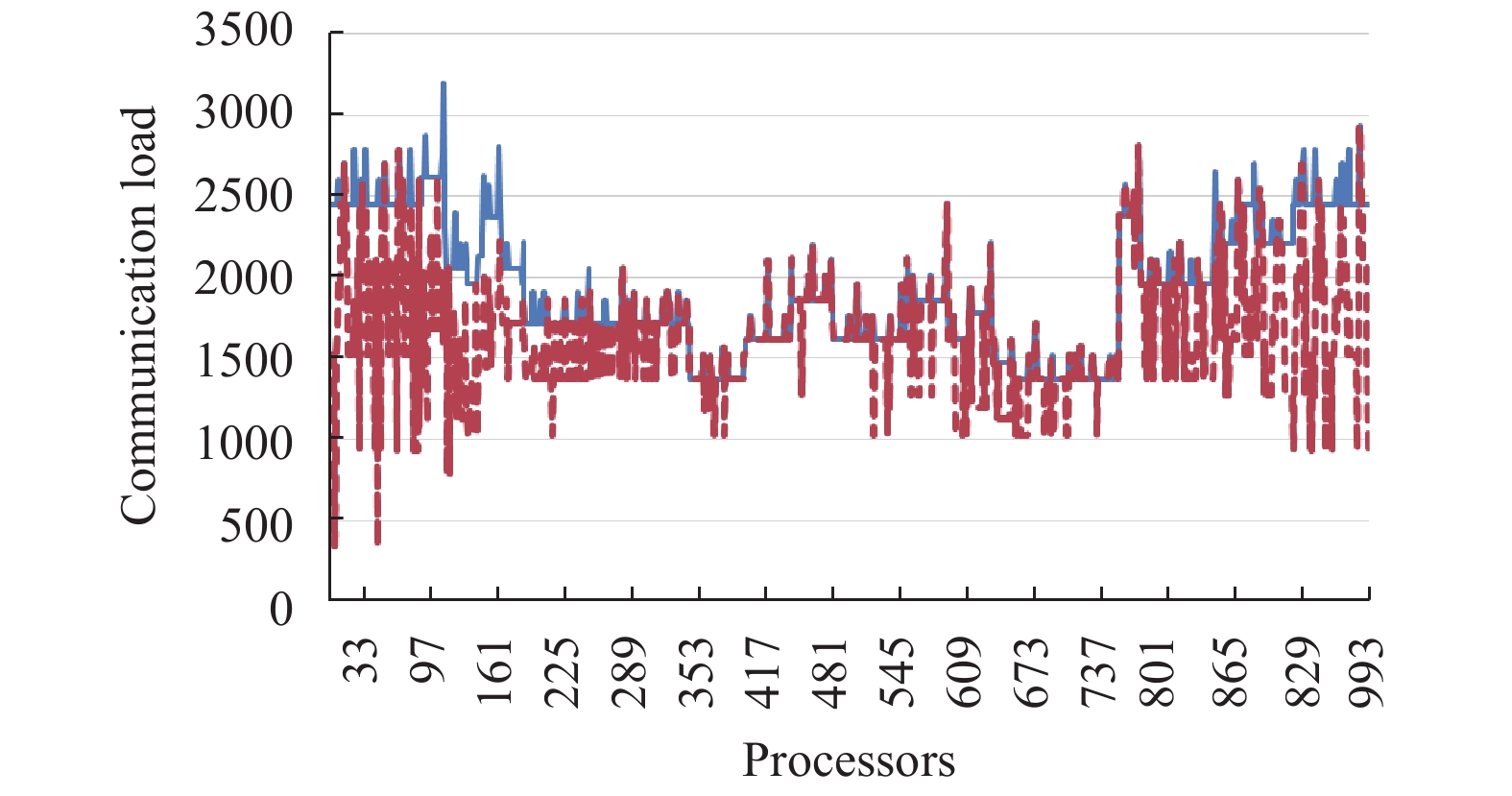
在不同规模的测试中, 统计各个进程内需要与其他进程内需要交换插值信息的网格单元, 作为通信量比较的依据. 图7-图10展示了不同规模测试优化前后的通信量对比, 实线表示采用循环分配法依此分配各个网格块时, 每个进程内的重叠插值信息通信量; 虚线表示采用优化算法后, 每个进程内需要通信的插值信息. 测试结果表明本文提出的混合重叠网格方法可扩展应用至千核规模的重叠网格模拟, 在不同规模下, 各个进程的通信量基本平衡, 通信优化算法能够有效减少进程间插值信息的传递.

|
图 7 128核测试通信量优化效果 |
|
图 8 256核测试通信量优化效果 |

|
图 9 512核测试通信量优化效果 |
|
图 10 1024核测试通信量优化效果 |
在并行测试过程中, 将执行混合重叠网格方法的预处理流程分解为7个部分, 分别统计这7个部分的运行时间. 这7个部分包括:
(1) 多层背景网格建立Background time.
(2) 计算各个网格单元的体积Volume time.
(3) 计算各个单元的到最近物面距离Distance time.
(4) 网格块的剖分Split time.
(5) 建立网格间插值关系和重叠权重系数Overset time.
(6) 发送网格块信息和重叠关系至各个进程Sendrecv time.
(7) 隐式挖洞标识IHC time.
统计的时间结果如表1所示, 展示了从128到1024和时不同处理环节消耗的时间, 从统计结果看, 计算网格标记属性的体积和最短壁面距离所消耗的时间最少, 建立插值关系是整个流程中最耗时的部分, 随着测试规模的扩大, 网格块规模的减少而耗时减少; 网格信息发送至各进程的时间耗时较多并随着测试规模扩大而减少; 隐式挖洞标识的时间基本不随规模增大而变化.
| 表 1 重叠网格不同环节时间对比(单位: s) |
4 结论
本文采用多层嵌套的背景网格替代空间区域的结构网格, 建立了笛卡尔辅助网格+多块结构网格的混合网格系统. 通过辅助网格实现洞边界的快速确定和网格间插值关系的快速建立, 在此基础上实现了混合网格的并行重叠流程. 通过定义重叠区域网格权重、部件网格与背景网格绑定的方法, 建立了混合网格的并行分配模式, 有效减少重叠插值信息在各进程间的通信, 并实现计算负载和通信负载在各个进程的均匀分配. 测试表明该方法可应用于数千万量级的重叠网格系统, 可扩展至千核规模, 高效的实现多个物体构成的复杂网格系统的重叠关系建立.
| [1] |
张来平, 常兴华, 赵钟, 等. 计算流体力学网格生成技术. 北京: 科学出版社, 2017. 3–15.
|
| [2] |
Benek J, Steger J, Dougherty FC. A flexible grid embedding technique with application to the Euler equations. Proceedings of the 6th Computational Fluid Dynamics Conference. Danvers, MA, USA. 1983. 373–382.
|
| [3] |
Meakin RL. Composite overset structured grids. In: Thompson JF, Soni BK, Weatherill NP, eds. Handbook of Grid Generation. Boca Raton, FL, USA: CRC Press, 1999. 11-1–11-20.
|
| [4] |
王文. 结构重叠网格方法及其并行算法研究与应用[学位论文]. 北京: 北京航空航天大学, 2017.
|
| [5] |
范晶晶, 阎超, 张辉. 重叠网格洞面优化技术的改进与应用. 航空学报, 2010, 31(6): 1127-1133. |
| [6] |
Lee Y, James D. Baeder, Implicit hole cutting–A new approach to overset grid connectivity. Proceedings of the AIAA 16th Computational Fluid Dynamics Conference. Orlando, FL, USA. 2003. 2003–4128.
|
| [7] |
Lee Y, Baeder J. High-order overset method for blade vortex interaction. Proceedings of the AIAA 40th Aerospace Sciences Meeting & Exhibit. Reno, NV, USA. 2002.
|
| [8] |
Landmann B, Montagnac M. A highly automated parallel Chimera method for overset grids based on the implicit hole cutting technique. International Journal for Numerical Methods in Fluids, 2011, 66(6): 778-804. DOI:10.1002/fld.2292 |
| [9] |
Kenway GK, Mishra A, Secco NR, et al. An efficient parallel overset method for aerodynamic shape optimization. Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Grapevine, TX, USA. 2017.
|
| [10] |
Bhagwandin VA, Sahu J. Numerical prediction of pitch damping stability derivatives for finned projectiles. Proceedings of the 29th AIAA Applied Aerodynamics Conference. Honolulu, HI, USA. 2011.
|
| [11] |
Murman SM. Reduced-frequency approach for calculating dynamic derivatives. AIAA Journal, 2007, 45(6): 1161-1168. DOI:10.2514/1.15758 |
 2019, Vol. 28
2019, Vol. 28



