2. 河海大学 计算机与信息学院, 南京 210008
2. College of Computer and Information, Hohai University, Nanjing 210098, China
随着经济环境的高速发展, 众多企业步入科学化管理时代, 但企业管理人员对企业的销售预测管理方面仍有疏漏, 甚至出现了各种问题. 比如管理人员常用的销售预测模型为专家法, 就是靠有经验者的从事经验来对销售进行人为主观预测, 与本文提出的改进BP神经网络算法相比有这快速、简单的优点. 但同时也有不可弥补的缺点, 每位专家的预测可能不一样, 带有严重的差异性与客观上的不可靠性. 还有时间序列方法中最为简单的指数平滑法[1], 通过不同的权重来控制预测的精度, 但是随着预测时间的延长精确率会大打折扣. 再者如ARIMA模型, 相对于前两者就较为复杂, 其原理是利用历史销量对未来销量进行预测, 但是ARIMA模型的建立, 需要数据集具有趋势性强的特点, 对于趋势性弱的数据集, 则通过ARIMA模型得到的结果预测效果也不理想.
作者就以上3种预测方法的优缺点, 提出进行改进优化后的BP神经网络算法预测模型, 同时利用指数平滑法和遗传算法模型得到的结果与改进后的BP神经网络算法进行对比实验, 以验证其在准确度、对数据集趋势性依赖强度、预测时间长度失准度方面的优化提升.
1 优化BP神经网络的算法设计基础 1.1 时间序列模型时间序列, 是一组按时间顺序排列并随时间的变化而变化的数据序列[2]. 一个时间序列往往是由上两点或多点以变化的方式叠加或耦合起来的.
所选择的二次指数平滑法[3]处理数据可预防实际在时间序列出现直线形式的上下波动时产生的“滞后”现象[4], 并能自动识别数据模式的变化, 加以调整.
1.2 BP神经网络BP神经网络是带有隐含层的多层前馈网络, 是一种误差反向传播算法[5]. 此算法由信息正向传递和误差反向传播组成, 其基本原理是不停地修正网络中各层节点的权值、阈值, 直到网络输出达到目标输出值, 且具有很好的泛化能力.
2 优化BP神经网络的具体算法设计 2.1 算法原理可泛化型时间序列校正下的遗传算法优化BP神经网络预测模型(简称TC_GA_BP神经网络预测模型), 使用了合并传统BP神经网络以及遗传算法[6–8]对BP神经网络进行改进, 利用时间序列预测值和改进后的GA_BP神经网络[9–11]进行“误差值”比较, 利用时间序列模型预测结果误差呈增函数关系的特点, 使用其与GA_BP神经网络的差值进行一元线性回归[12,13], 讨论出两者之间误差值的函数拟合关系, 再利用拟合函数[14]进行误差测算, 最后通过两者误差规律, 校正其中一者的预测值, 这里选择对GA_BP神经网络的预测值进行校正, 从而最后得到校正后的预测值.
已知BP神经网络算法的收敛速度较慢是由于BP神经网络算法究其本质是梯度下降法, 因为需要优化的目标函数非常复杂, 所以出现“锯齿形现象”在所难免, 这会使得BP算法低效. 与此同时正也因为目标函数的复杂, BP网络的神经元输出在接近0或1的情况下, 会出现一些平坦区, 在这些平坦区内, 权值误差变化很小, 使训练过程几乎停滞. 再者为了使网络执行BP算法, 必须预先赋予网络的步长更新规则, 这样也会使得算法低效. 就此引发出利用遗传算法优化BP神经网络的优化方式.
而在面临小数据量的处理情况时, 由每个个体独立讨论是有可能利用线性关系处理非线性问题, 真实值与预测值之间一定会存在误差. 故令距离为
为解决此问题, 对时间与真实值之间的误差
得到了一元回归模型的具体表达, 利用时间序列预测值减去回归模型得出的对应误差量, 得出修正E值, 即可以用来的再次优化GA_BP神经网络的传递权值和各个神经元的阈值, 以达到利用校正函数[15]修正GA_BP神经网络的目的.
在GA_BP神经网络的优化后, 依旧存在步长
| $\Delta {w_{ij}}(n) = \alpha \Delta {w_{ij}}(n - 1) + \eta {\delta _i}(n){y_j}(n) $ | (1) |
其中, 第二项是传统BP神经网络的修正量, 第一项就是上文提及的优化因子,
| $\Delta {w_{ij}}(n) \approx \eta \sum\limits_{t = 0}^n {{\alpha ^{n - 1}}{\delta _i}(t){y_j}(t) = - \eta \sum\limits_{t = 0}^n {{\alpha ^{n - 1}}\frac{{\partial \xi (t)}}{{\partial {w_{ij}}(t)}}} } $ | (2) |
当
结合上面分析结果, 二次改进后
| ${w_{ij}}(t + 1) = {w_{ij}}(t) - \eta {d_j}{O_j} + \alpha \left\{ {{w_{ij}}(t) - {w_{ij}}(t - 1)} \right\}$ | (3) |
其中,
经过对GA_BP神经网络预测值修正后, 可以得到误差平方和
已知输出层的输出误差
| ${E_c} = \frac{1}{2}\sum\limits_j {{{\left( {O_j^{k - 1}\left( {W,X} \right) - {y_j}} \right)}^2}} $ | (4) |
其中,
| ${E_c} = \frac{1}{2}\sum\limits_{k = 1}^l {{{\left[{d_{{}_k}} - f(ne{t_k})\right]}^2} = } \frac{1}{2}{\sum\limits_{k = 1}^l {\left[{d_k} - f\left(\sum\limits_{j = 0}^m {{w_{jk}}{y_j}} \right)\right]} ^2}$ | (5) |
最后推导至输入层
| $ \begin{aligned}[b] {E_c} &= \frac{1}{2}\sum\limits_{k = 1}^l {{\left\{ {d_k} - f\left[\sum\limits_{j = 0}^m {{w_{jk}}f(ne{t_k})} \right]\right\} }^2} \\ &=\frac{1}{2} {\sum\limits_{k = 1}^l {\left\{ {d_k} - f\left[\sum\limits_{j = 0}^m {{w_{jk}}f\left(\sum\limits_{i = 0}^n {{v_{ij}}{x_i}} \right)} \right]\right\} } ^2} \end{aligned}$ | (6) |
根据误差就可以得出权值函数
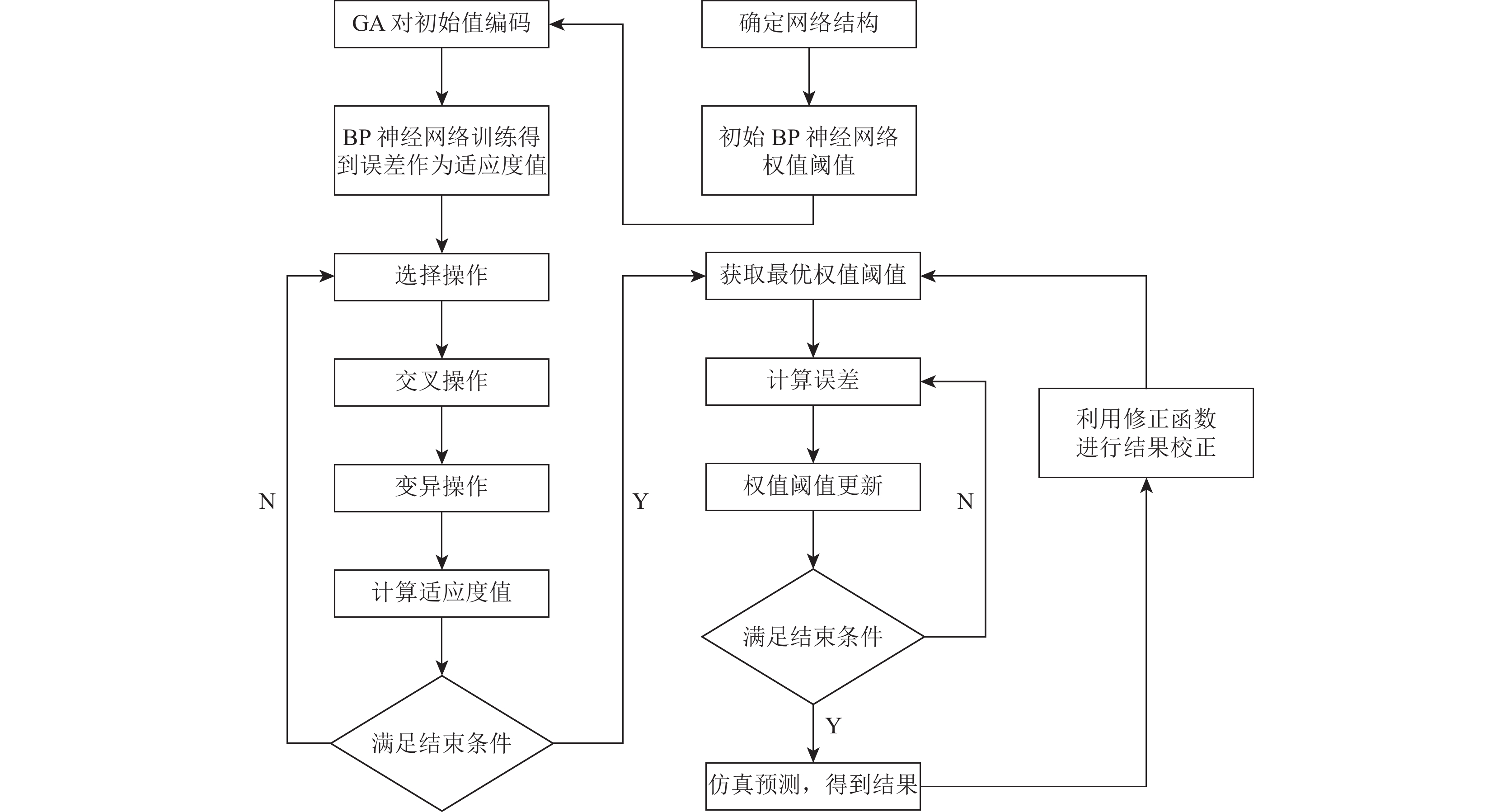
基于优化BP神经网络的流程图如图1所示.
|
图 1 基于优化BP神经网络的流程图 |
3 优化BP神经网络在Kaggle竞赛数据集中的应用
利用上文提到的算法对Kaggle竞赛数据集[16]进行销售预测.
3.1 时间序列仿真实验使用由Kaggle竞赛提供的Restaurant Revenue Prediction数据集, 抽取其中的一家名为“Stanbul”的餐厅作为实验对象进行仿真实验. 利用已有销售额统计的50条数据, 使用时间序列预测模型的二次指数平滑法对其进行时间序列仿真预测, 而且与一次指数平滑法的结果做对比仿真结果如图2、图3.

|
图 2 一次平滑指数预测图 |
|
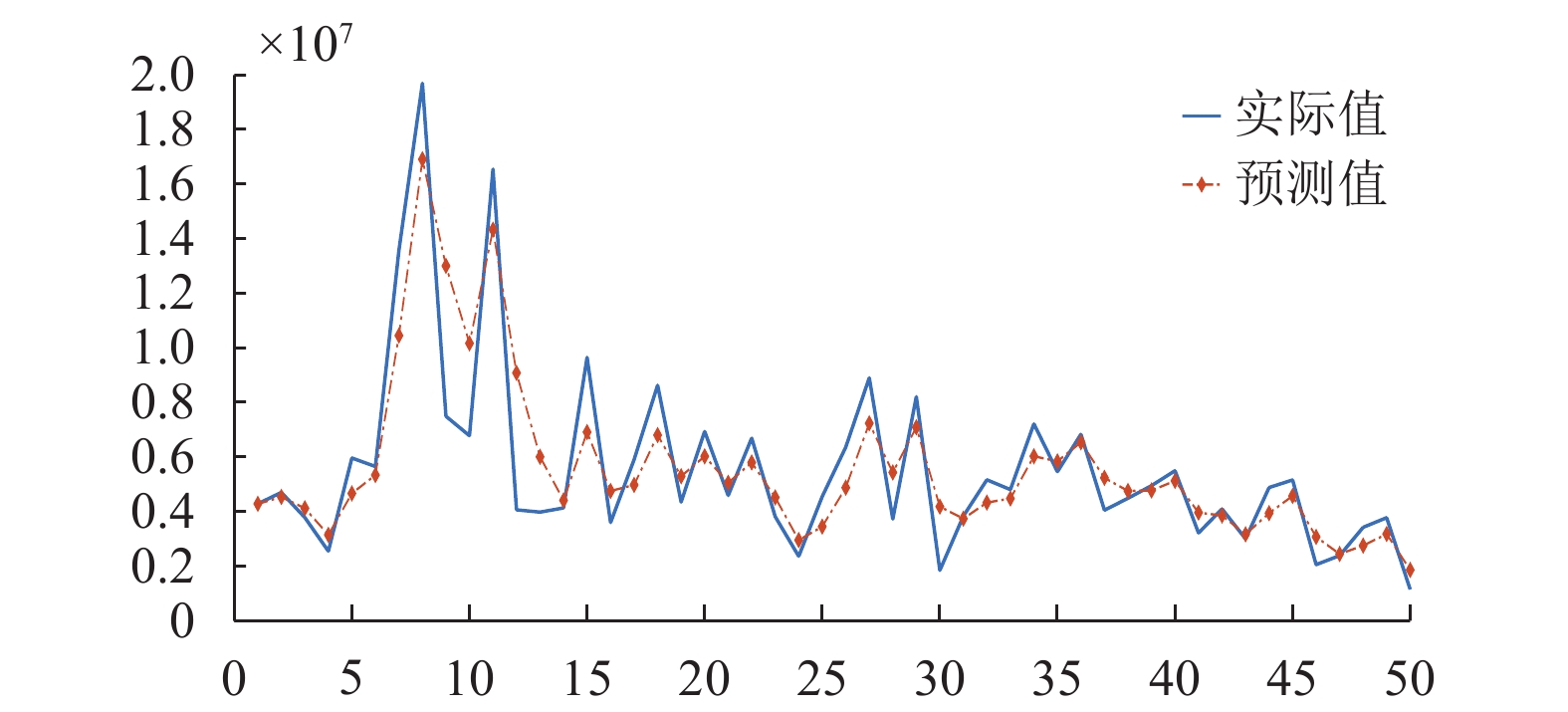
图 3 二次平滑指数预测图 |
经过试验, 实验结果与理论预测完全符合, 一次指数平滑法在25个数据集仿真结果中, 出现了大量的滞后反应, 无论α=0.2, α=0.5还是α=0.8都无法改变滞后反映, 这也正体现了二次指数平滑预测较高的准确度(误差率25.7471%), 为下文提供了可行方案.
3.2 算法实现过程将优化后的 BP 神经网络算法, 与经典 BP 神经网络、时间序列模型、遗传算法改进神经网络进行销售预测的比较. 在已有销售额统计的50条数据中, 抽取其中的25条作为仿真训练集, 剩余的25条作为仿真验证集, 用于验证误差. 3种算法的误差对比分析如图4、图5和图6所示.

|
图 4 传统BP神经网络预测图(误差为50.2401%) |
|
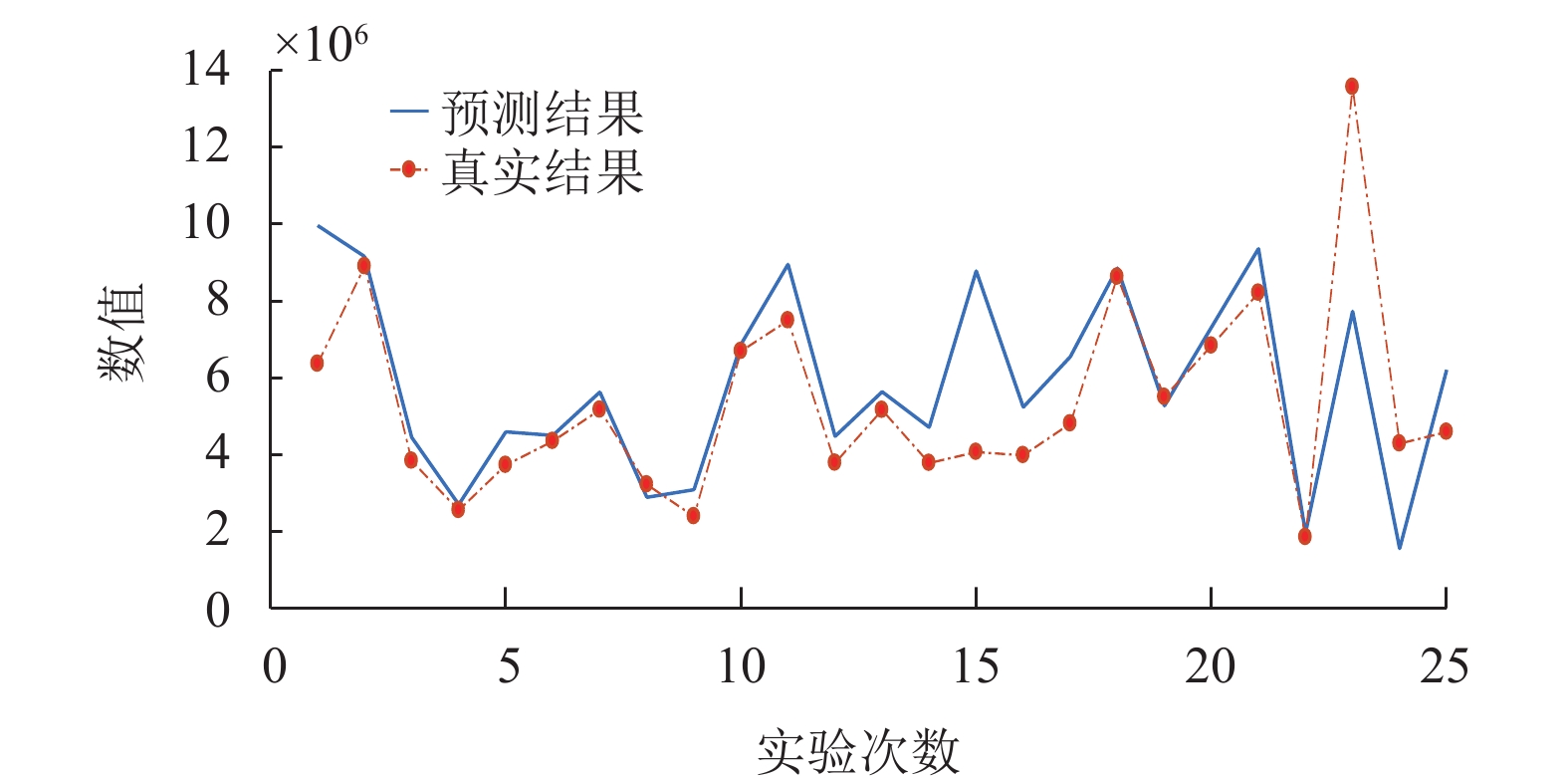
图 5 遗传算法BP神经网络预测图(误差为23.629%) |
|
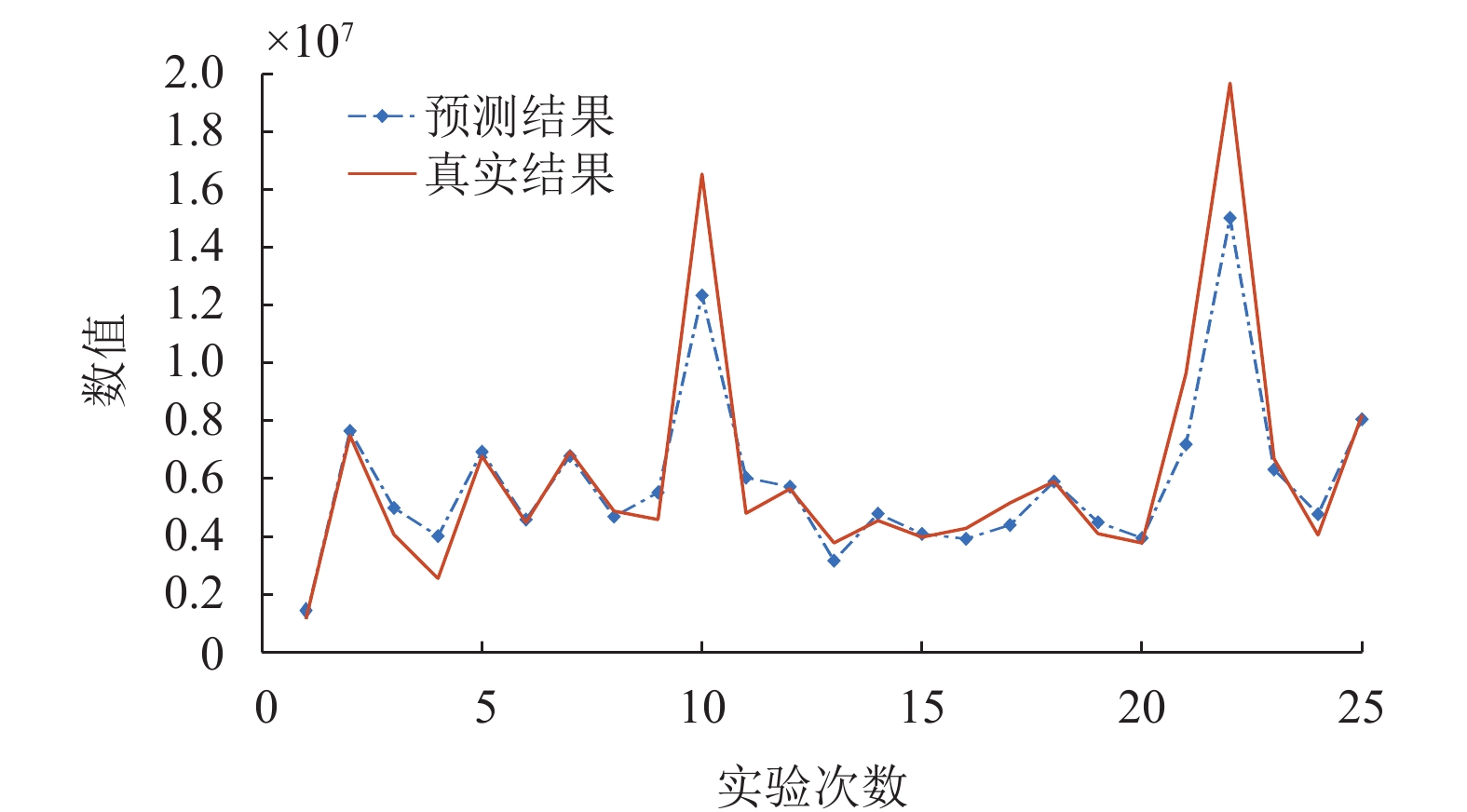
图 6 TC_GA_BP神经网络预测图(误差为12.088%) |
由图像直观看出, 在相应的被修正点上, 预测值比遗传算法改进BP神经网络的结果预测值更为接近真实值结果, 而误差率也降至约12%, 提高近11%. 由此可知, 新提出的TC_GA_BP神经网络模型的预测输出结果, 在预测的准确度上大大改善, 比另外3种模型的预测更加接近未来真实值.
3.3 结果分析部分预测结果如表1所示.
| 表 1 预测结果对比 |
统计数据表明, TC_GA_BP神经网络预测模型的仿真效果最好, 达到12.088%; 而传统BP神经网络的结果误差最大, 达到50.2401%, 被认为是不可信的预测模型; 时间序列预测模型和改进后的BP神经网络都有良好的仿真实验, 但仍没达到TC_GA_BP神经网络的预测精度. 因此TC_GA_BP神经网络在同属性的数据集预测上优于其他3种预测模型.
4 总结与展望文章首先采用时间序列模型减少源数据的误差, 利用优化后的BP 神经网络, 建立起适当的销售预测模型, 并具体应用于某数据集中. 实验表明优化后的 BP 神经网络算法在提高了预测准确度和收敛速度的同时, 也简化了网络结构, 减少了数据的误差. 由于可利用于训练网络的数据量太少, 导致网络训练情况不佳, 达到的准确度不是太高. 如需进一步的深入研究, 可考虑在现有算法基础上训练更多的数据集.
| [1] |
焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年: 回顾与展望. 计算机学报, 2016, 39(8): 1697-1717. |
| [2] |
吴晓峰, 陈垚彤, 赵桂彩. 金融时间序列组合预测模型与方法. 中国市场, 2019(9): 47. |
| [3] |
王林. 指数平滑法在配件销售预测中的应用. 物流科技, 2019, 42(3): 45-48. |
| [4] |
张天作. 基于FPGA的矩阵乘法实现方案在全连接深度神经网络前向传播中的性能评估[硕士学位论文]. 北京: 北京邮电大学, 2018.
|
| [5] |
付敏娟. 基于指数平滑与神经网络模型的太阳能热水器销售预测[硕士学位论文]. 湘潭: 湘潭大学, 2017.
|
| [6] |
高航. 基于改进遗传算法的反向传播神经网络拟合LED光谱模型. 激光与光电子学进展, 2017, 54(7): 072302. |
| [7] |
胡叶容. 基于GA-BP神经网络的电容层析成像图像重建. 电子技术与软件工程, 2018(23): 83-84. |
| [8] |
杨佳欣. 国际贸易对我国通货膨胀的多元线性回归分析. 西部皮革, 2019(5): 134-135. DOI:10.3969/j.issn.1671-1602.2019.05.080 |
| [9] |
张冰. 基于曲线拟合函数和GPU的大规模地形无缝渲染技术研究[硕士学位论文]. 太原: 太原理工大学, 2018.
|
| [10] |
盖立平, 刘爱连, 刘义军, 等. 能谱CT成像中测量位置与校正系数的关系. 中国组织工程研究, 2016, 20(31): 4677-4686. DOI:10.3969/j.issn.2095-4344.2016.31.017 |
| [11] |
董志贵, 王福林, 宋庆凤, 等. 基于BP神经网络的无约束优化方法. 统计与决策, 2019, 35(1): 79-82. |
| [12] |
冯娇, 李红朴. 基于优化小波神经网络的宏观经济预测技术研究. 现代电子技术, 2019, 42(7): 181-183. |
| [13] |
吴诗辉, 张发, 李正欣, 等. 基于神经网络的仿真优化算法设计. 系统工程与电子技术, 2019, 41(6): 1324-1335. DOI:10.3969/j.issn.1001-506X.2019.06.21 |
| [14] |
刘亚丽, 李英娜, 李川. 基于遗传算法优化BP神经网络的线损计算研究. 计算机应用与软件, 2019, 36(3): 72-75. |
| [15] |
周朝进, 王玉珍. 优化BP神经网络算法在农资网站销售预测中的应用. 邵阳学院学报(自然科学版), 2019, 16(1): 52-59. |
| [16] |
邓仲华, 刘斌. 数据挖掘应用热点研究——基于Kaggle竞赛数据. 图书馆学研究, 2019(6): 2-9, 23. |
 2019, Vol. 28
2019, Vol. 28



