一起突发事件将触动一组应急流程, 在一起石化安全引发的火灾事件中, 需要消防、卫生、安全、工程等部门的联合处置, 消防团队与医疗团队, 安全团队与医疗团队, 工程团队与安全团队等之间密切交流和协调, 其中位置区域的最低阈值是应急资源调度的区域边界, 往往调度距离强度关系最近的团队, 结果显示, 距离最近的团队之间的协调救援, 应急结果还有很大的提升空间, 处置结果跟执行实体的协作度有关, 实体及团队之间的协作活动成为决定应急处置结果的核心过程, 需要在应急指挥决策中针对不同的应急事件活动特征, 充分衡量应急团队、实体的优先级, 包括救援团队的实体调度, 突发事件中, 通用型调度方案表现出极其不协调的实体资源分配的多种特征, 影响救援结果.
1 研究现状近年来, 在应急团队的研究中, 有不少研究成果, 有研究团队基于人类动力学理论对应急核心要素进行研究[1], 并利用社团检测等方法对应急情景等复杂情形下对主体、资源、客体等深入研究[2]. Liu D等人对复杂社区的检测中, 对复杂情景下, 个体与个体之间的关系进行研究 [3]. 许多研究团队在成员调配和团队生成研究领域有所成就, Ly[4]等人提出用决策树学习方法进行成员分配; Liu YB[5]等从人工智能角度, 基于机器学习提取成员技能特征, 以便在团队生成时完成技能匹配度; Xu RB[6,7]等在考虑主体成员、资源客体及相关约束关系等属性基础上提出成员分配模型, 兼顾了多种执行模式; 在基于最小冗余度等方面的研究, 在团队生成上都有不错的效果.
同时, 基于活动的协作模式方面, Meddah等[8]提出基于流程挖掘协作模型; Lappas等[9]基于社交网络(SNS)理论研究团队的生成, 把成员间的合作代价作为算子, 以此增加团队的协作效率; Kargar等[10]基于距离之和、领导者距离等方面提出Top-k团队取代过去的最优团队.
目前并没有针对突发事件中的实体成员的最优化调配和应急队伍间协调等方面的进行研究, 本研究的主要任务针对突发事件这一特定的环境, 加入应急救援体系中的必需因子和属性, 是一项有价值的工作, 为应急决策奠定数据基础.
2 相关概念及问题描述 2.1 相关概念定义1. 突发事件(Emergency Event, EE)包括事件开始时间(Emergency Event start time, EEst), 也可以是子事件的开始时间、事件发生地(Emergency Event scene, EEs)可以是事件发生转移地点的集合、事件结束时间(Emergency Event end time, EEet)、事件主体(Emergency Event subject, EEsub)、事件客体(Emergency Event object, EEobj)、事件名称(Emergency Event name, EEname)具有唯一性、事件中活动(Emergency Event activity, EEact), 形式化描述Ee为EE的子集, Ee={Eest (t1, t2, …tn), Ees(s1, s2, …, sn), Eeet (et1, et2, …, etn), Eesub (石油, 热水, 卡车, …), Eeobj (人, 动物, 生物, …), Eename (爆炸、倒塌、塌陷、起火, …), Eeact (喷水, 掩埋, 起吊, …)}.
突发事件EE的实例模型, 如EE1=(2018/2/5/17:18, 浙江省台州市天台县赤诚街道足馨堂足浴店, 2018/2/5/24:00, 大火, 人, 火灾, EEact (冲水、救人、紧急救护、防爆、升降输送)), 应急执行实体(Entity person, Ep)=(消防人员、医疗人员、物管等应急人员).
定义2. 应急救援流程模型(Emergency Rescue Process Model, ERPM), 应急协同部门接警后, 根据应急需求调配自身资源, 以应急救援为目标, 产生的救援活动组成的序列(Activity[n],A)={a1, a2, a3, …, an}, Set表示活动与活动之间的顺序的有序对元组, S
定义3. 应急活动模型. 突发场所环境处理(EvP): a1=气体隔离和净化活动、a2=倒塌物处理、a3=对有电的环境断电处理等.
(1)应急主体处理(SP): a1=对着火点洒水、a2=对着火点干冰处理等.
(2)应急客体处理(OP): a1=救援被困人员、a2=使用探测、a3=抢护其他物资等.
(3)突发现场态势固化处理(SaP): a1=现场评估、a2=确认显态触发点终止、a3=确认隐态触发点终止等.
(4)应急救援处置结果评估(RA): a1=救援经济价值评估、a2=救援人数评估. 最终生成Activity[n]={EvP, SP, OP, SaP, RA}, 其中应急活动与各子活动间的关系可以重复, 如可以出现Activity[n]={EvP, SP, OP, SP, OP, SaP, RA}的情形, 表示SP、OP的优先级不具有明显的优先关系, 需要并发进行, 符合突发事件的特征, 则得到
定义4. 应急库包括案例库和预案库, 用EECB表示, EECB={Ee1, Ee2, Ee3, …, Eei, …, Een}, 按照事件主体进行类别划分, Aee={a1, a2, a3, …, ai,…, an}出现在EECB1中的活动的集合, 轨迹Ti=<Eei, 0; Eei, 1; …; Eei, j >表示应急案例库中所有事件按时间组成的序列, 其中 Eei, j表示第i个应急案例中的第j个发生的事件, 使用活动表示轨迹Ti=<ai, 0; ai, 1; …; ai, j >.
定义5. 应急执行实体Ep={(ai∣Epi), ai∈Aee, Epi∈Ep}, 表示在突发事件中Epi执行救援活动ai; 则实体轨迹定义为EpTi=<ai, 0∣Epi, 0; ai, 1∣Epi, 1; …; ai, j∣Epi, j > 表示应急救援实体的时序活动序列. 同时应急执行实体也可以是应急团体, 里面包含了若干个实体序列.
定义6. 应急执行实体的技能贡献度, Epi在一次应急救援中该项技能使用次数与EECB中所有该项技能使用次数的比值, 比值为uEpi∈(0, 1), 反映实体的某项技能熟练程度.
定义7. 应急活动连续性用
| $conti{n_{{a_i},{a_j}}} = {\left\{ 1 + {e^{ - \theta (f{a_i},{a_j} - f')}}\right\} ^{ - 1}}$ | (1) |
其中,
定义8. 应急执行实体的关系强度(Relationship Strength, RS), 由实体间的属性相似度决定, 而执行实体的归属又是一个重要特征指数, 假设Epi和Epj之间有m种交互关系, m∈N.x(Epi)和y(Epj)表示实体属性向量, RS<Epi, j>表示两个实体间的潜在关系强度S(x(Epi), y(Epj), 表示实体相似度向量.
| $ \begin{split} &P\left( {RS\left\langle {{E_{{P_{i,j}}}}} \right\rangle ,m|{\rm{x}}\left( {E{p_i}} \right),y\left( {E{p_j}} \right)} \right)\\ &=\! P\left( {RS\!\left\langle {E{p_{i,j}}} \right\rangle |x\left( {E{p_i}} \right),y\left( {E{p_j}} \right)} \right)\prod\limits_1^m \!{P\left( {m|RS\!\left\langle {{E_{{P_{i,j}}}}} \right\rangle } \right)} \end{split} $ | (2) |
它是满足高斯分布的.
| $P\left( {RS\left\langle {E{{\rm{p}}_{{\rm{i}},j}}} \right\rangle |x\left( {E{p_i}} \right),y\left( {E{p_j}} \right)} \right) = N\left( {S\left( {x\left( {E{p_i}} \right),y\left( {E{p_j}} \right)} \right),v} \right)$ | (3) |
其中, v是方差, 可取小于1的值, 如果归属团队一致, 则v值稍大.
| $P\left( {{\rm{m}} = 1{\rm{|}}RS\left\langle {E{p_i}_j} \right\rangle } \right) = {\left\{ {{\rm{1 + }}\mathop e\nolimits^{ - \left( {RS + b} \right)} } \right\}^{ - 1}}$ | (4) |
其中, RS是关系强度, 得到一个P值.
定义9. 应急执行实体的协作度[11].
| $coo{p_{{a_i},{a_j}}} = {\left\{ {R{S_{{a_i},{a_j}}} + {e^{ - \theta \left( {{t_{{a_i},{a_j}}}} \right)}}} \right\}^{ - 1}}$ | (5) |
其中,
应急案例库不完备的性, 及对救援实体和救援活动的分析相对薄弱, 造成各大组织应急演练, 依照固定模式执行, 未着重考虑应急资源调度中, 针对某一应急活动, 应急实体的协调性、应急活动连续性、应急关系强度等核心要素之间的关系, 需要在应急预案中搞清应急实体、距离、应急活动等之间的协同, 文中建立真实案例知识库和人工预案库, 来进行数据分析, 扩充智能推理的语料库. 解决应急案例库中的数据段还不完备, 本文主要贡献应用于基于CBR应急预案的生成, 给决策者提供辅助决策.
应急预案和应急演练的焦点在应急处置的应急实体, 其具有的技能贡献度和实体间的协作度, 往往影响整个应急处置的结果, 以往的应急预案中采用的是通用性评估, 事实上, 应急实体的特征显著, 可以从技能贡献度uEpi角度挖掘, 充分考虑实体与实体间的协作能力, 在实际救援中, 才不会因为实体间协调不好, 导致应急任务的拖延, 措施救援时间, 由此产生的应急预案, 为应急执行团队的组建奠定基础.
在应急管理和应急事件处置中, 调配资源和人员, 受到地域行政区划的制约, 通常这样几种情形, 不管事发地位置, 直接选择行政管理区域的中心位置进行调配, 或者挑区域内经验丰富的团队, 实际上, 在有些救援中距离关系强度好的团队和实体, 在协作能力上表现出色, 选择哪个团队需要考虑地理位置这一最低阈值, 同时需要考虑团队间的协作和对应急活动的适应度, 文中在活动频度角度一并作了考虑. 在应急活动的制定上, 环境因素复杂会影响协调, 在应急预案中, 确认活动与活动之间的基本优先关系尤为必要.文中定义了活动之间的连续性
文中数据集包括网络案例数据库和人工案例数据库, 真实数据集是从万维网上爬取了近十年应急救灾案新闻数据达数十万条, 包括相关案例的论文研究, 由于相关数据公开度不一致, 出现结构化数据中部分字段缺失或模糊, 但对本文研究未造成很大的影响, 本文中建立了相对完备的应急预案库, 对于数据稀疏的矩阵区域, 用人工案例库进行校正, 人工数据率为μ=[0.3, 0.4], 消除了噪音等不合理数据, 得到的应急相关要素间的关系和发展趋势, 数据结论对应急预案、演练有极其重要的作用.
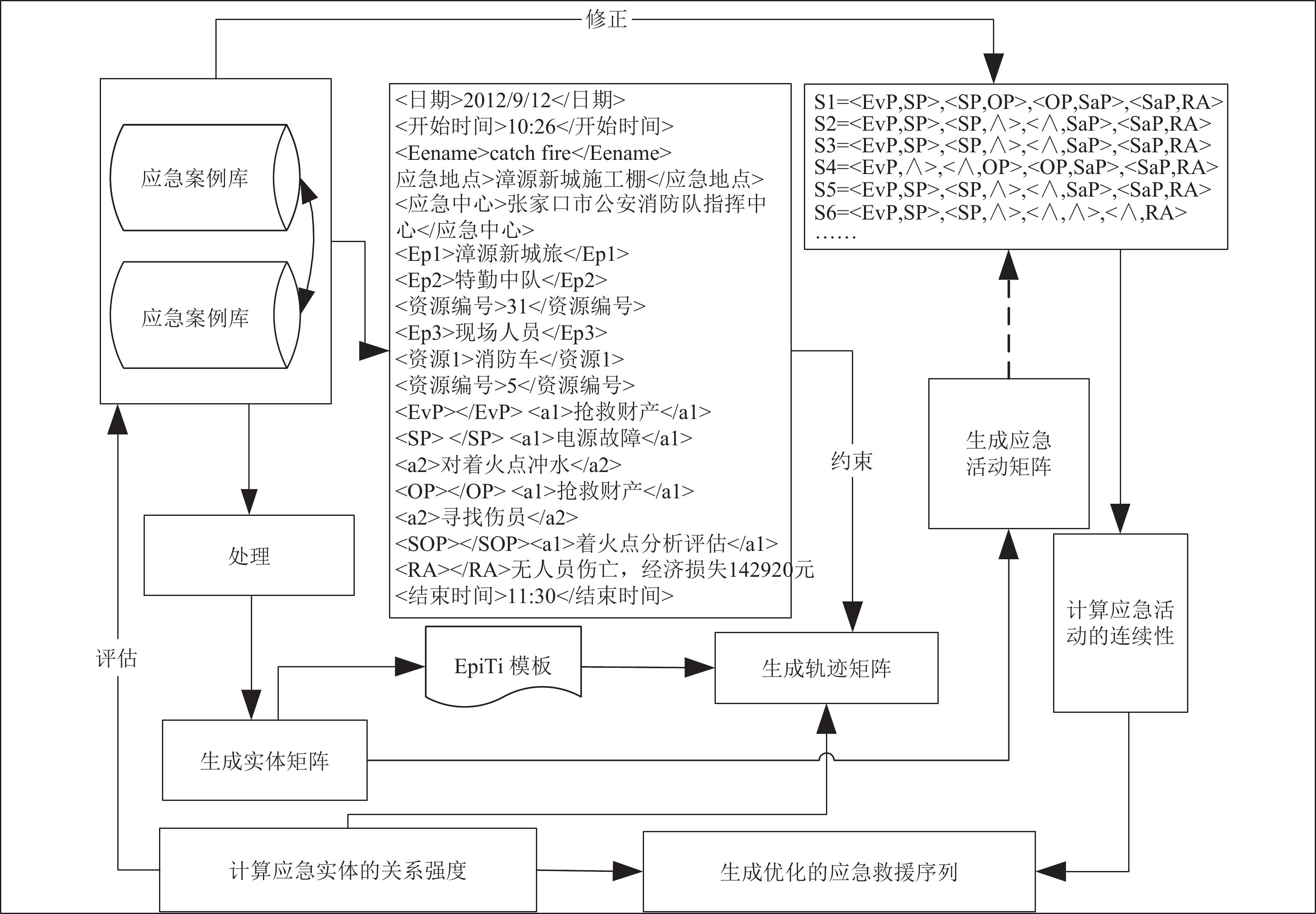
3 方法 3.1 应急执行实体和应急活动的优化基于应急案例、应急预案数据集, 对应急执行实体和应急活动的最优化分配, 实现优化应急活动的序列整体框架如下(见图1):
首先, 对应急案例库预处理的数据清洗中, 将案例库中的非必要字段剔除, 如原采集网页中的标准等, 生成XML结构数据字典, 并按地域进行分类, 模糊行政区域边界(如图2), 即边界区域附近的案例互相包含.
|
图 1 基于案例数据集的实体、活动抽取框架 |
|
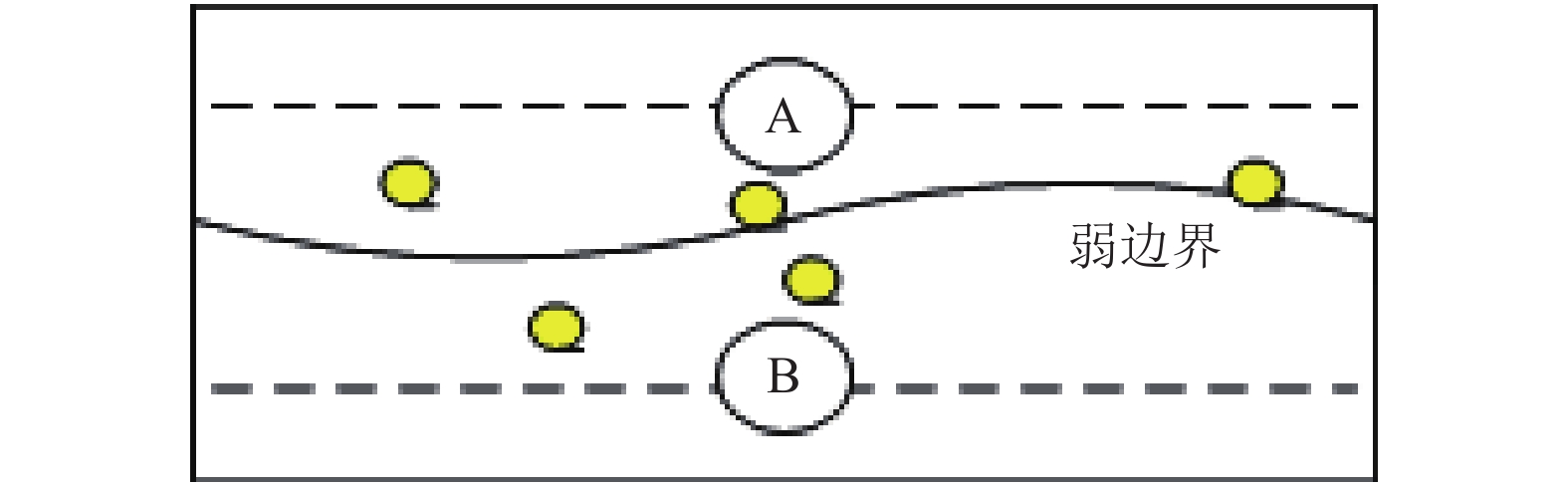
图 2 边界示意图 |
对于地理位置分别属于A、B的两个位置区域中, A和B为区域中心, 地理位置阈值最高, 越往边缘, 地理阈值越小, 称为弱边界, 分布在弱边界中的事件, 分别属于两个行政区域, 这样的划分, 打破了以往的行政区划中心, 而以距离强度来分布.
将同地理区域的案例根据式(1)–式(5), 计算成应急实体轨迹矩阵和活动轨迹矩阵. 稀疏矩阵中的数据元素为“∧”, 则添加人工案例库数据进行修正, 修正系数μ=0.3. 在对应急案例库和预案库过程中, 会存在出现噪音数据和冗余数据, 本文通过标签化处理, 对应急时间、属性等关键信息的标准化处理, 并剔除异常数据值, 采用经典的Needleman-Wunsch算法[12]来实现, 例如, 文中定义活动间的有序对元组Set,
基于上文中数据, 计算应急活动的连续性
为了挖掘应急案例库中具有高协作度的实体, 基于应急实体轨迹、实体技能贡献度等实现算法1, 首先计算所有的实体轨迹的矩阵, 再基于此矩阵, 通过最小地域置信度阈值和技能贡献度等过滤得到具有高协作度的实体即高协作模式.
基于算法得到实体间协作能力的一般矩阵和有高协作能力的实体矩阵.
3.3 挖掘高连续性活动基于应急案例库, 挖掘应急实体活动的轨迹挖掘同区域活动的协作度.首先初始化应急活动轨迹矩阵, 计算一般活动的连续度contin, 根据整个案例库中所有活动为基数, 计算某一个活动出现的频度F′, 产生θ调优值, 可以根据不同的值得到几组结果, 进行迭代.
4 结果
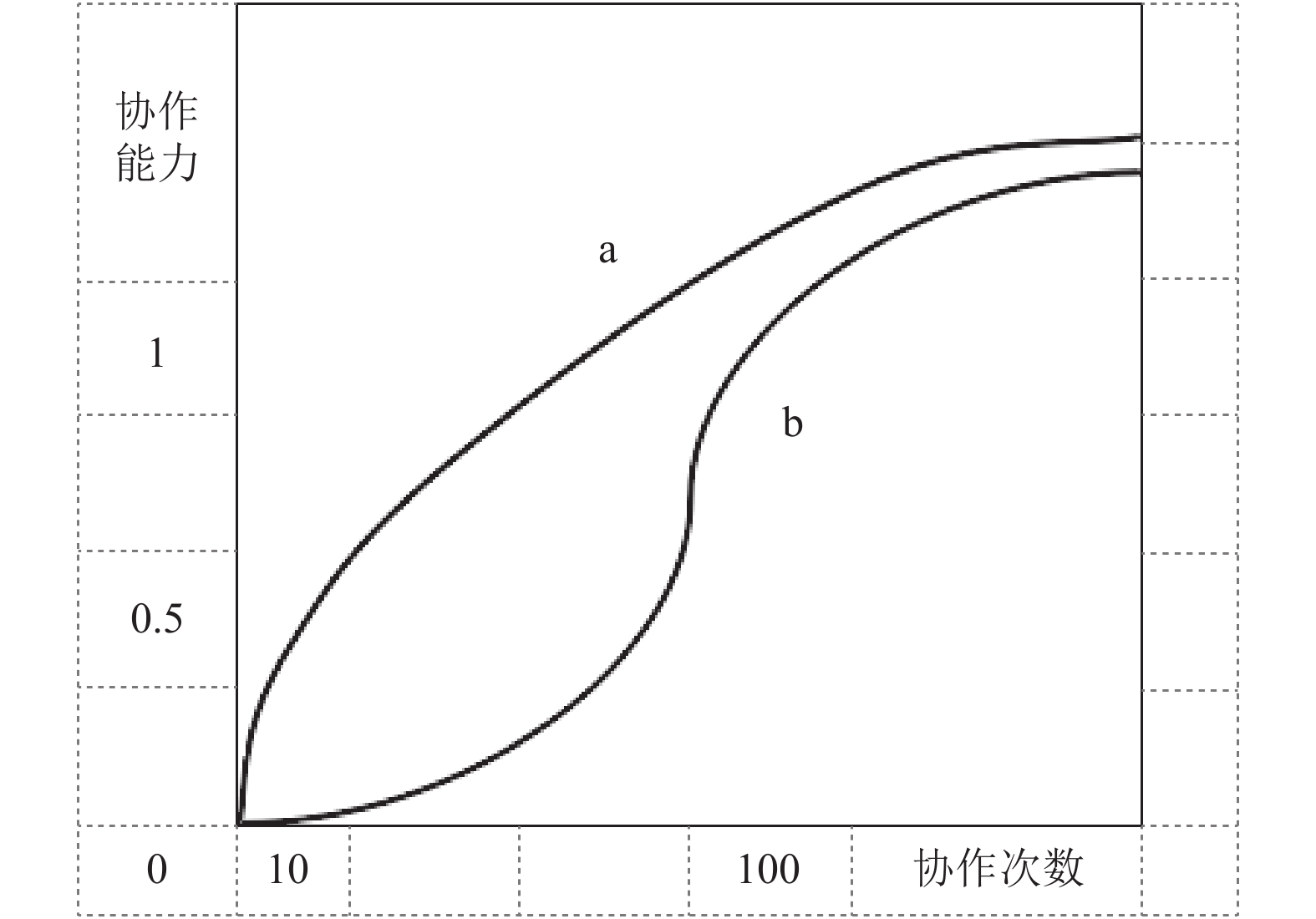
图3中曲线a可以看出某城市中, 不同应急消防团队实体在协作次数和协作能力上的表现, 随着合作次数的增加稳步提升, 可以超过指数1, 在尾部也表现为增幅放缓, 跟合作多次之后, 采用经验和旧案例判断有关, 需要适应性更新案例库和预案库.
|
图 3 应急实体协作次数与协作能力关系 |
曲线b可以看出, 在同属同一位置区域中, 位置强度关系显著的应急实体间的协作能力, 医护实体和消防实体之间随着协作次数的增加, 协作能力稳步增强, 增长期间的会有波动, 跟参与的活动有关, 在协作一定次数之后, 反而协作能力会出现下降, 因为在多次协同之后, 经验占据整个决策的主导, 导致经验主义的误判, 在应急预案的生成中, 要重点规划合作次数较少的和合作有一定次数的.
图4中曲线a可以看出边界消防实体和中心消防实体之间的关系, 随着协作的次数, 它们的协作能力稳步提升, 跟消防团队的调配和管理方式相关, 消防实体在应急中任务明确,平时应急演练标准化程度高的作用体现.
曲线b可以看出在同区域的医护实体实体和中心位置的医护实体之间的协调度随着协作次数的增长而增长, 呈现泛指数分布, 中间反而会出现协作能力的上升, 协调能力可以达到0.5, 跟实体的技能度相关, 也反应了在边界区域的实体之间的协作能力也有表现强的. 在应急预案中不能仅仅关注行政区域中心的应急实体, 这种现象在大规模应急事件中会有所体现, 往往调度一个区域的医护实体不够的时候, 需要调度多个医护实体才能应对的突发事件, 需要考虑此种情形.

|
图 4 边界实体协同次数与协作能力的关系 |
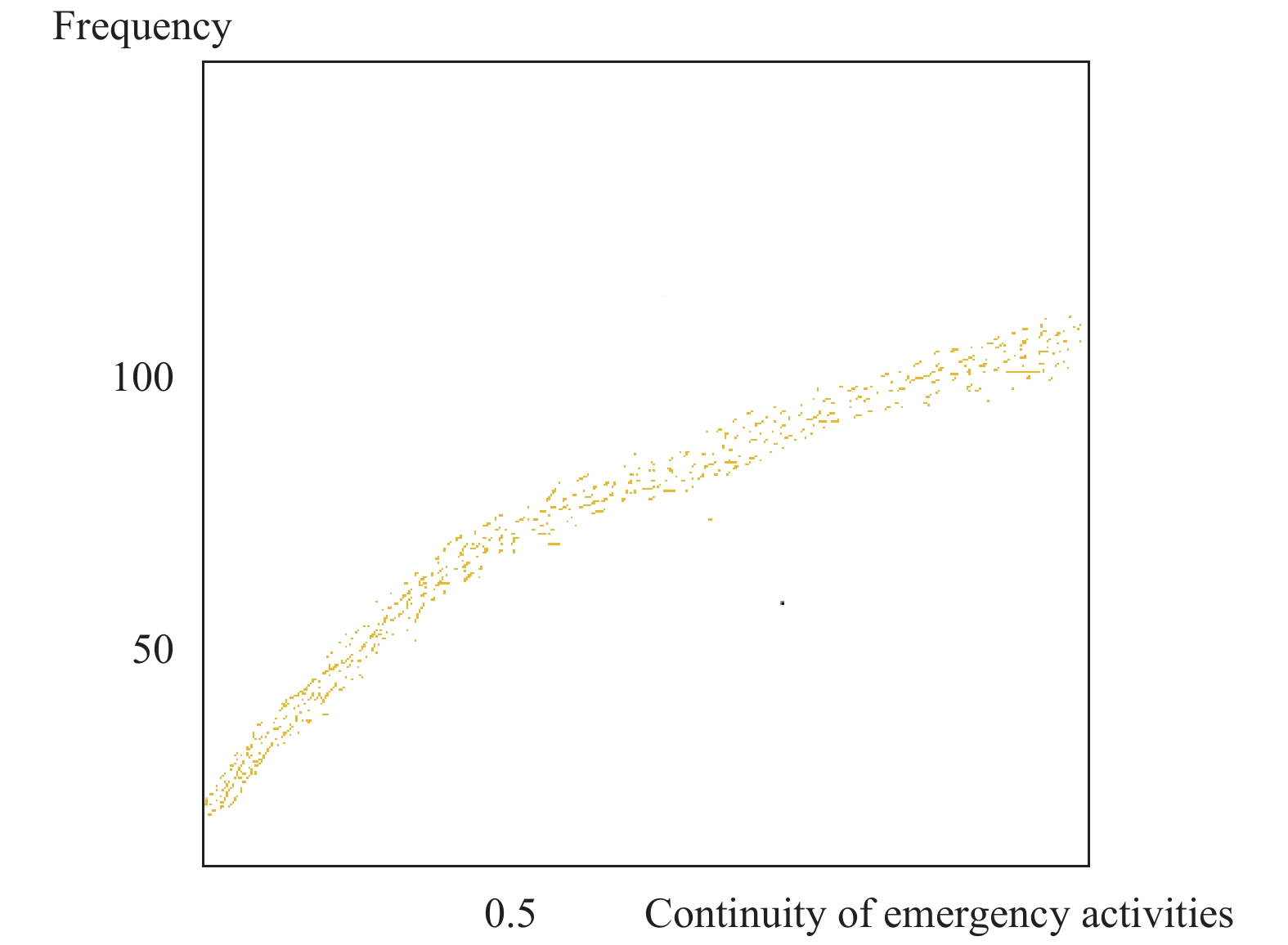
从图5曲线上可以看出, 应急活动的连续性与应急案例库中的应急频率直接成正比. 曲线不平滑, 分段明显. 应急预案库包括应急预案和旧预案. 基于某一特定领域的案例库的完整性, 针对某一特定应急活动的演练越多, 应急活动的连续性就越强. 很强, 反映了应急预案的重要性. 事实上, 应急计划通常非常相似, 但事件的情况是独一无二的. 同类突发事件发生频率较高, 具有预警作用. 同样, 数据库中相应应急活动的频率也下降了. 如图所示, 当活动连续性为零时, 数据中的活动频率不是零. 数据库中存在单一的活动关系, 不一定没有活动连续性, 这与实际的应急指挥一致. 有时根据现场情况, 临时产生应急动员方案.
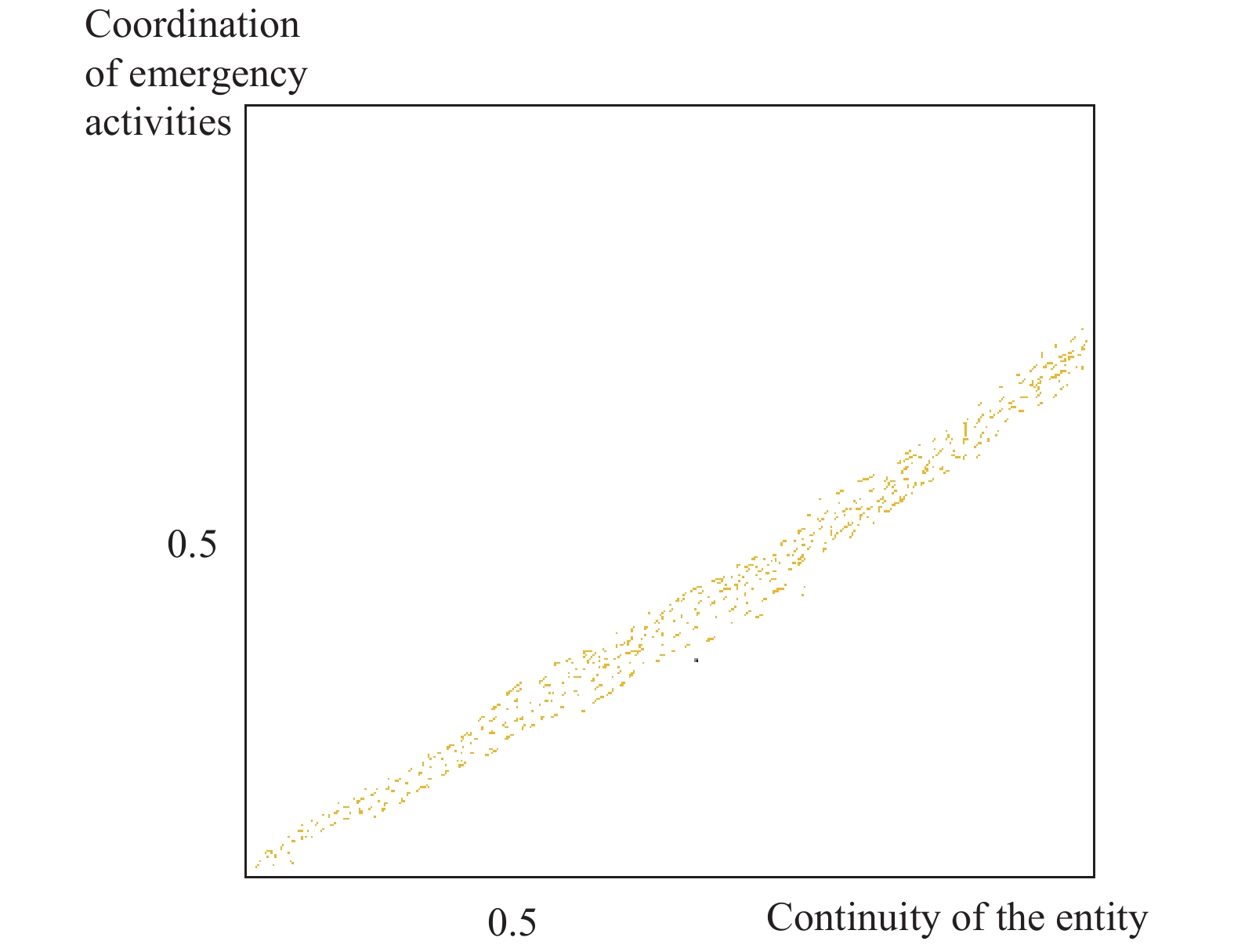
在图6中, 横轴表示活动的连续性, 纵轴表示实体协作的程度. 曲线表现出相似的二项分布, 反映了应急活动的连续性与应急实体协作程度的关系. 在紧急事件中, 应急活动的连续性和参与应急活动的实体的协作程度相互影响. 应急活动的连续性越高, 应急实体的协作程度越高. 同样, 应急协作程度越高, 应急活动的连续性越高, 应急活动越活跃. 当动态连续性超过指数1时, 由于应急实体协调次数增加, 活动与活动的优先关系设计, 曲线中后部的增长速度加快. 当活动连续性值接近1.8时, 不再上升, 与实际应急处置环节一致. 每个突发事件的处置过程都有其自身的特点. 在实际的应急指挥中, 需要通过应急实体的协调和应急活动的连续性, 直接确定应急处置的时间. 时间是紧急处置中最昂贵的成本之一, 首先应该考虑到时间, 提高应急响应的满意度.
|
图 5 频率和应急活动的关系 |
|
图 6 活动连续性与实体协作度的关系 |
5 基于应急案例库的应急预案产生的框架
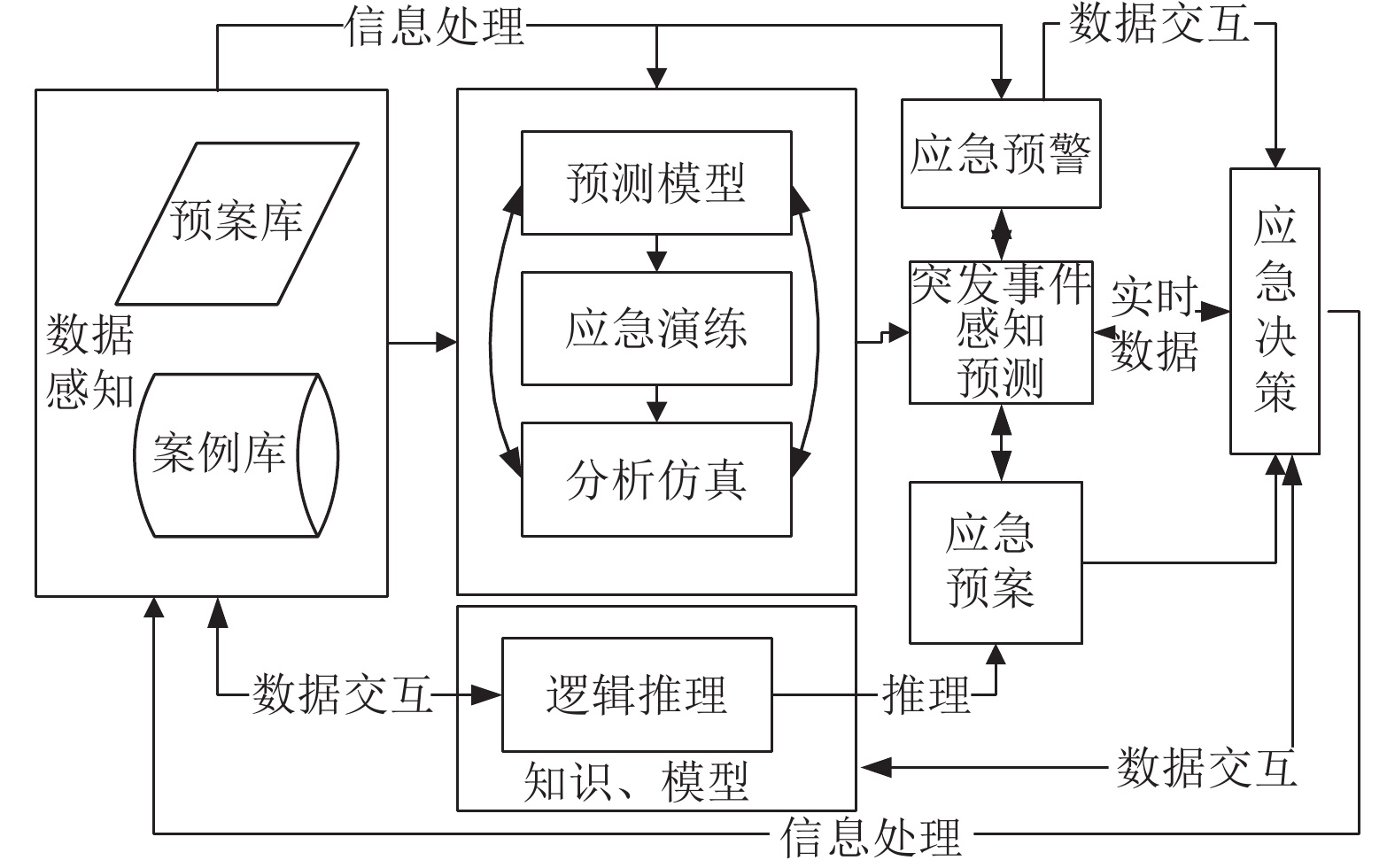
如图7, 基于案例库和预案库进行数据处理, 其中的数据有实时从外部感知的数据, 这样可以动态的调整数据, 在数据分析的基础上建立预测模型, 为应急演练、仿真分析等作准备, 应急预警、应急预案和应急决策是建立在对数据逻辑推理的基础上进行的, 可以提供辅助决策的准确度, 应急个体的属性包括应急执行实体的各种态势, 应急活动的各项指标, 结合实际感知到突发事件的数据, 为应急决策提供理论基础.
|
图 7 基于应急案例库的应急预案产生的框架 |
6 结论
本文以应急案例库和预案库为基础, 对应急实体和应急活动的必要属性进行定义, 对应急执行实体的技能贡献度, 应急实体的关系强度、应急活动的连续度等做了细致分析, 用实验数据得出同一区域同一类型应急实体之间的协作能力和协作次数之间的关系, 不同实体在同一区域的协作能力的趋势, 位置关系强度较弱的实体之间的协作能力关系, 在此基础上产生的应急预案, 有效性和针对性大幅提高, 更合理的选择利用经验知识, 缩小误判率, 文中考虑的因素相对比较理想化, 影响应急事件演变的因素很多, 需要根据确定的某一事件做细化, 今后工作中, 将从下面3点不断深入应急知识库中的知识表示和知识学习, 提高知识库和应急要素对接的精准度, 提高产生应急预案的准确度和可行度, 其一, 实验的数据量直接影响了结果, 由于案例库的不足, 预案库支持率上升, 使得有些实验数据跟现实情况有差值, 还需要不断的爬取新的数据量, 使案例库不断完备. 其二, 影响应急救援结果的因素, 不止文中着重研究的应急实体和活动等要素, 还有诸多突发的要素, 文中就这两点从团队组合的角度去考虑, 有许多救援其实跟资源有关, 文中这点比较薄弱. 其三, 在应急区域边界的划分上, 各个区域有所不同, 文中采用了模糊化的手段, 需要分区域进行考虑, 严格划分位置区域, 本文是理想位置状态.
| [1] |
Jiao PF, Cai F, Feng YD, et al. Link predication based on matrix factorization by fusion of multi class organizations of the network. Scientific Reports, 2017, 7: 8937. DOI:10.1038/s41598-017-09081-9 |
| [2] |
Liu X, Wang WJ, He DX, et al. Semi-supervised community detection based on non-negative matrix factorization with node popularity. Information Sciences, 2017, 381: 304-321. DOI:10.1016/j.ins.2016.11.028 |
| [3] |
Liu D, Liu X, Wang WJ, et al. Semi-supervised community detection based on discrete potential theory. Physica A: Statistical Mechanics and Its Applications, 2014, 416: 173-182. DOI:10.1016/j.physa.2014.08.051 |
| [4] |
Ly LT, Rinderle S, Dadam P, et al. Mining staff assignment rules from event-based data. In: Bussler CJ, Haller A, eds. Business Process Management Workshops. Berlin: Springer, 2006. 177–190.
|
| [5] |
Liu YB, Wang JM, Yang Y, et al. A semi-automatic approach for workflow staff assignment. Computers in Industry, 2008, 59(5): 463-476. DOI:10.1016/j.compind.2007.12.002 |
| [6] |
Xu RB, Liu X, Xie Y, et al. A Gaussian fields based mining method for semi-automating staff assignment in workflow application. Proceedings of 2014 International Conference on Software and System Process. Nanjing, China. 2014. 178–182.
|
| [7] |
许荣斌, 鲍广华, 杨培全, 等. 基于最大依赖度及最小冗余度的员工协作优化策略. 计算机集成制造系统, 2017, 23(5): 1014-1019. |
| [8] |
Meddah I, Khaled B. Discovering patterns using process mining. International Journal of Rough Sets and Data Analysis, 2016, 3(4): 21-31. DOI:10.4018/IJRSDA.2016100102 |
| [9] |
Lappas T, Liu K, Terzi E. A survey of algorithms and systems for expert location in social networks. In: Aggarwal CC, ed. Social Network Data Analytics. Boston: Springer, 2011. 215–241.
|
| [10] |
Kargar M, An AJ. Discovering top-k teams of experts with/without a leader in social networks. Proceedings of the 20th ACM International Conference on Information and Knowledge Management. Glasgow, UK. 2011. 985–994.
|
| [11] |
俞东进, 王娇娇, 柳诚飞. 基于协作模式的工作流最优员工分配方法. 软件学报, 2018, 29(11): 3340-3354. DOI:10.13328/j.cnki.jos.005483 |
| [12] |
Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 1970, 48(3): 443-453. DOI:10.1016/0022-2836(70)90057-4 |
 2019, Vol. 28
2019, Vol. 28



