生产调度问题, 就是在有限资源与时间内, 最大效率的完成指定的生产目标. 关于生产调度问题的研究一直是现今学界研究的热点. 一些学者对单机批调度问题展开了研究. Uzsoy[1]最先考虑了差异工件单机批调度中最小化最大完工时间Cmax的问题, 并且证明其为NP-hard类问题. Lee[2]在Uzsoy[1]的研究基础上, 在单机批调度问题中考虑了工件动态到达约束. Mosheiov和Oron[3]与Cheng等[4]均考虑了其他调度目标, 其中Mosheiov和Oron[3]考虑了单机批调度中最小化总流经时间问题, 而Cheng等[4]考虑了单机批调度中最小化模糊完工时间问题. 刘娟和陈华平[5]提出了一种求解单机批调度问题的改进PSO算法, 并验证了算法的性能. 吴愁[6]在单机批调度问题研究中考虑了能耗情况. 而并行批调度研究是对单机批调度问题的进一步拓展. 一些学者对不同算法在并行批调度问题中的应用进行了研究. Damodaran和Chang[7]提出了一些启发式算法来求解最小化制造跨度并行批调度问题. 然而这些算法的局限之处在于, 求解大规模工件问题得到的解的质量要弱于一些智能优化算法. 郭乘涛和江志斌[8]提出了一种混合型蚁群算法来解决并行批调度中工件动态到达组批难问题; 王庆[9]提出了一个混合粒子蜂群算法, 并将其运用于并行批调度问题研究之中. 程八一等[10]考虑了最小化联合成本并行批调度问题, 并设计了一种多项式时间近似算法. 李国臣等[11]和张震等[12]分别考虑了能耗约束和模具约束并行批调度问题.
本文对遗传算法在差异工件动态到达约束下并行批调度问题中的应用展开了研究. 首先根据问题假设建立了一个混合整数规划模型. 采用BF、ERT-LPT规则对工件进行分批排序. 然后设计了新的选择、交叉、变异操作并结合遗传算法进行求解.
1 问题描述本文研究了差异工件的并行批调度问题, 该问题的具体特征描述如下:
(1)差异工件集合
(2)批处理机器集合
(3)工件加工批次集合
(4)工件动态到达, 工件
(5)批的加工时间为批中工件最大的加工时间, 批的到达时间为批中最晚到达工件的到达时间;
(6)批的加工无法中断, 工件加工不允许抢占;
(7)优化目标是最小化制造周期, 即 makespan.
根据上述描述, 本研究差异工件的并行批调度问题的数学模型为:
| $Min \;\;\;{C_{\max }}$ | (1) |
| ${\rm{s.t.}}\;\;\;\;\sum\limits_{b = 1}^{\left| B \right|} {{x_{jb}}} = 1\;,\;\;\;\;j = 1,2, \cdots ,n$ | (2) |
| $\;\sum\limits_{k = 1}^m {{y_{bk}}} = 1\;,\;\;\;\;b = 1,2, \cdots ,\left| B \right|$ | (3) |
| $\;\sum\limits_{j = 1}^n {{s_j}{x_{jb}}} \le C\;,\;\;\;\;b = 1,2, \cdots ,\left| B \right|$ | (4) |
| $P{T_{bk}} \ge {p_j}{y_{bk}}\;,\;b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m;j = 1,2, \cdots ,n$ | (5) |
| $\;R{T_{bk}} \ge {r_j}{y_{bk}}\;,\;\;\;\;b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m;j = 1,2, \cdots ,n$ | (6) |
| $S{T_{bk}} \ge P{T_{b - 1,k}},\;\;\;\;b = 2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m$ | (7) |
| $\;S{T_{bk}} \ge R{T_{bk}},\;\;\;\;b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m$ | (8) |
| $\left\lceil {\sum\limits_{j = 1}^n {{s_j}} /C} \right\rceil \le \left| B \right| \le n$ | (9) |
| $\;C{T_{bk}}\; = S{T_{bk}} + P{T_{bk}},b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m$ | (10) |
| ${C_{\max }}\; \ge \;C{T_{bk}}\;,b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m$ | (11) |
| ${x_{jb}} \in \left\{ {0,1} \right\},j = 1,2, \cdots ,n;b = 1,2, \cdots ,\left| B \right|$ | (12) |
| ${y_{bk}} \in \left\{ {0,1} \right\},b = 1,2, \cdots ,\left| B \right|;k = 1,2, \cdots ,m$ | (13) |
式(1)表示的是本研究数学模型的优化目标; 式(2)表示的是一个工件只能分配到一个批次; 式(3)表示的是一个批次只能由一个机器进行加工; 式(4)表示的是同一批次所加工工件尺寸的容量约束; 式(5)表示在机器k上加工的批b的加工时间; 式(6)表示在机器k上加工的批b的到达时间; 式(7)、式(8)表示的是系统对批的开始加工时间的约束,即工件加工不允许抢占约束, 批中工件全部到达之后才能开始加工; 式(9)表示批的数量约束; 式(10)、式(11)表示的是模型制造跨度的计算方法; 式(12)、式(13)则是对两个0–1变量的描述.
2 遗传算法在并行批处理机调度中的应用自1975年Holland教授提出遗传算法以来, 由于遗传算法所具有的独特求解复杂的优化问题的优势, 大量学者对遗传算法的理论研究方向以及应用研究方向展开了深入研究. 本文就是对差异工件并行批调度问题中遗传算法应用方向展开研究的.
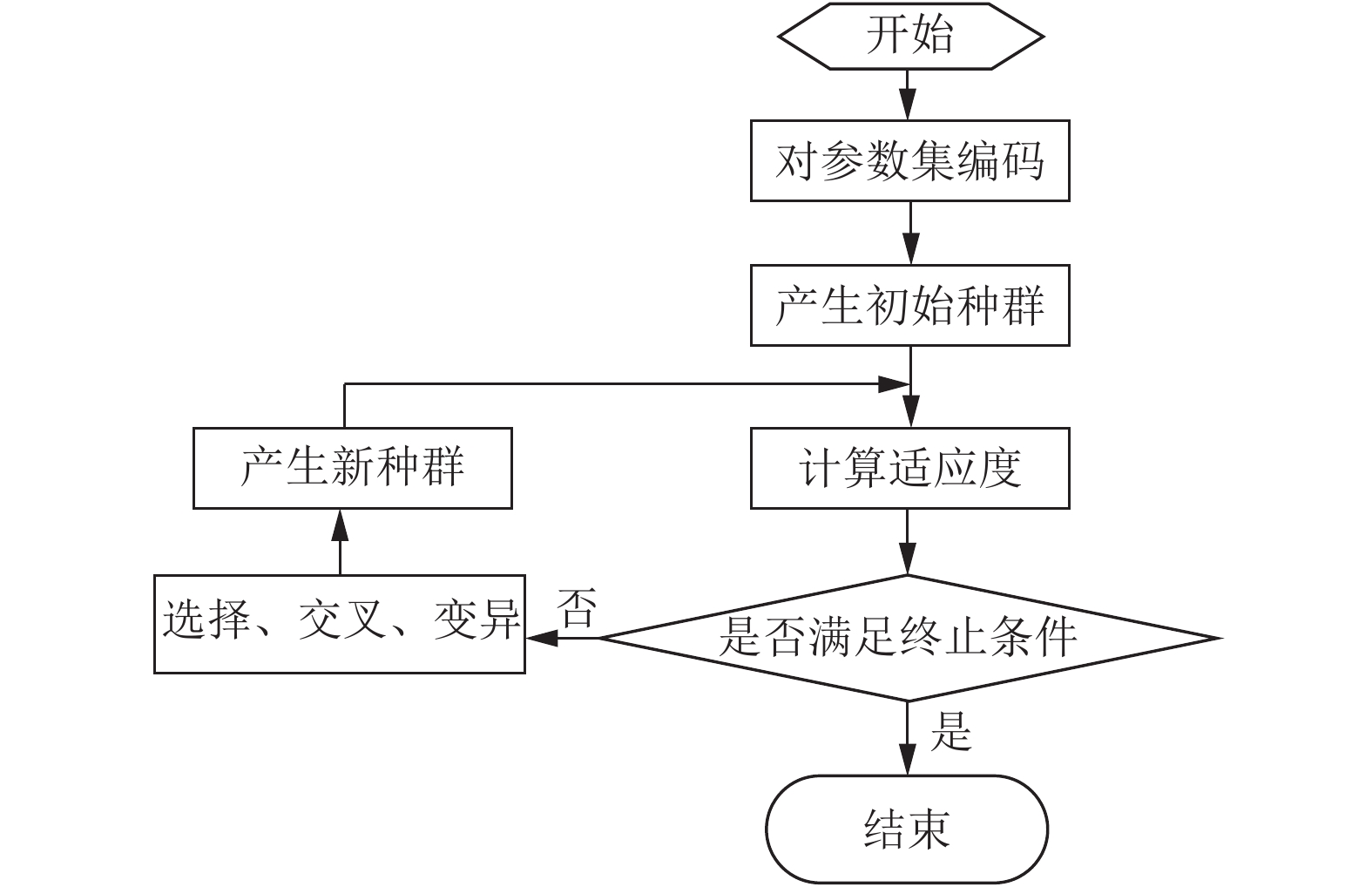
2.1 遗传算法简介遗传算法是通过模拟生物进化过程求得最优解的方法. 遗传算法一般计算流程如图1所示.
|
图 1 遗传算法计算流程图 |
2.2 编码与分批排序策略
常见用来求解批调度问题的编码方式有两种: 基于批和基于工件序列. 本文采用基于工件序列的编码方式, 即用一组1~n的数字排列代表一个可行解, 如表1所示.
| 表 1 基于工件序列的编码方式 |
不同的排列中工件的位置不同, 根据后面提出的调度策略可以生成不同的调度方案.
分批与排序是批调度中最重要的两个决策过程, 决策的好坏直接影响解的质量. 本文考虑采用BF规则进行分批, 采用ERT-LPT规则安排批在机器上的加工顺序. 两种规则的具体实现步骤如下:
BF规则:
(1)给定一个工件序列;
(2)选择序列中第一个工件, 在所有批中查找能容纳该工件且剩余容量最小的批, 并将该工件加入到该批中; 否则, 新建一个批并将该工件加入到新批中;
(3)重复步骤2, 直到所有工件完成分批.
ERT-LPT规则:
(1)计算所有批的到达时间、加工时间. 批的到达时间为批中最晚到达工件的到达时间, 批的加工时间是批中工件最大的加工时间;
(2)将批按到达时间的先后顺序排列, 若有多个批的到达时间相同, 则按照批的加工时间长短顺序进一步排列;
(3)选择当前处于空闲的状态的机器, 将批序列中首个批次安排在该机器上加工;
(4)重复步骤(3), 直到所有批调度完成, 最后计算makespan.
2.3 面向并行机批调度问题的遗传算法遗传算法是基于种群的进化算法, 通过染色体的选择、交叉、变异操作生成新一代种群, 然后在整个解空间迭代优化寻找最优解. Damodaran等[13]提出了一种遗传算法求解单机批调度问题. 本文在此基础上, 考虑新的选择、交叉、变异算子结合遗传算法对并行批处理机调度问题进行求解.
(1)选择
选择操作是首先寻找适应度较高的个体作为母本, 适应度用来评价个体的优劣程度. 根据前文提出的BF、ERT-LPT规则可以计算出个体的makespan值. 本文中选定以下公式作为适应度函数:
| $fitness(i) = \;{e^{ - {C_{\max }}(i)}}$ | (14) |
选取指数函数作为适应度函数, 是因为在公式中采用指数函数可以提高算法的收敛速度[14].
然后基于比例选择的方式挑选优势个体, 其中优势个体选择概率为:
| $ p(i) = \frac{{{\rm{ }}fitness{\rm{ }}(i)}}{{\displaystyle \sum\limits_{j \in pop} {fitness} (j)}} $ | (15) |
其中, pop为当代种群. 显然, 个体适应度越大, 被选择的几率越大.
(2)交叉
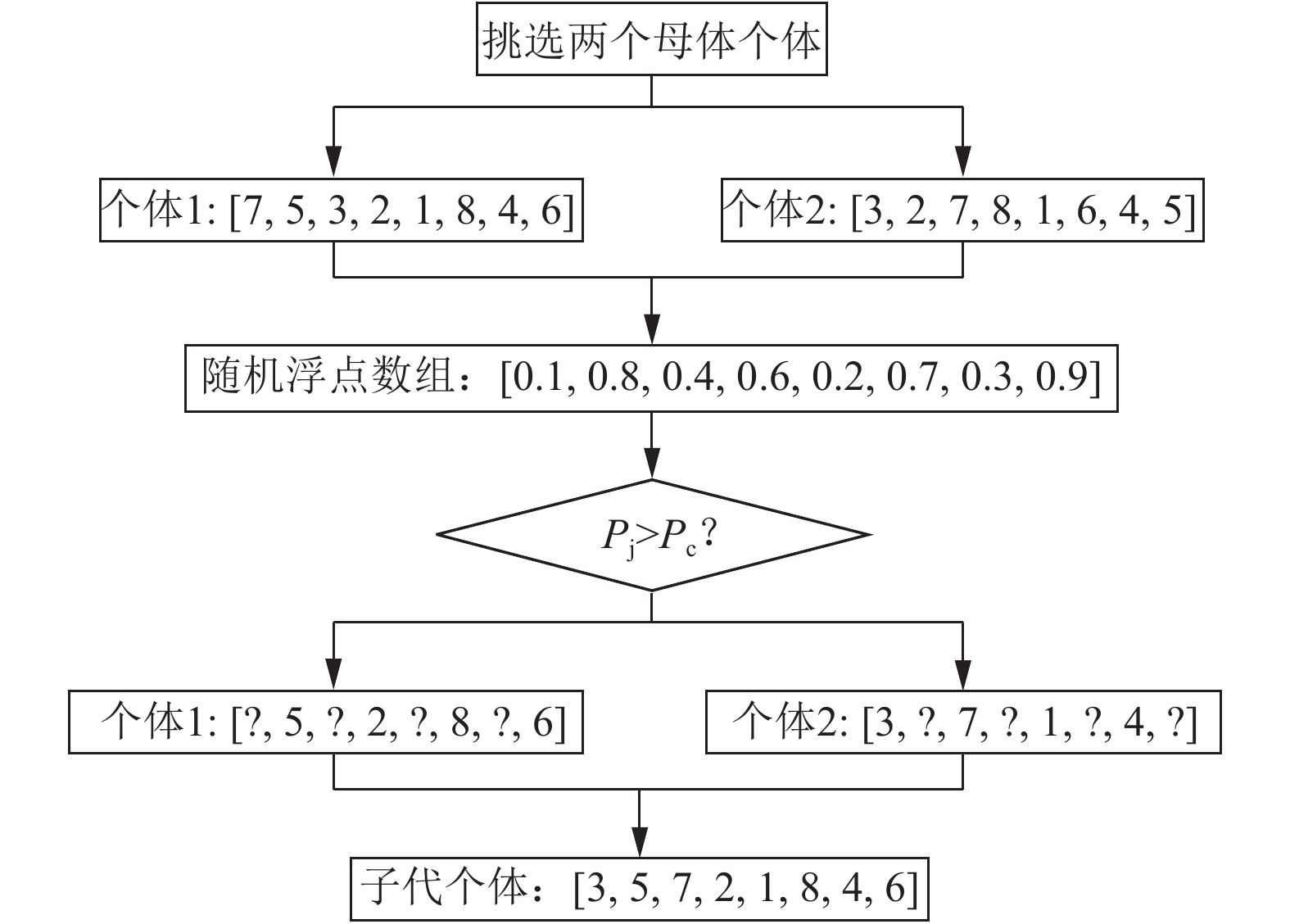
交叉操作是遗传算法中生成子代种群最有效、最直接的方法. 好的交叉策略能够提高算法的搜索能力, 节省运算时间. 常见的交叉操作有单点交叉、双点交叉. 本文通过利用一组随机浮点数组实现一种新的交叉方式, 具体如图2所示.
|
图 2 交叉操作 |
图2中, 我们先挑选工件规模为8的两个个体作为母本, 分别是: 个体1[7, 5, 3, 2, 1, 8, 4, 6]、个体2[3, 2, 7, 8, 1, 6, 4, 5]. 然后随机生成一组浮点数组[0.1, 0.8, 0.4, 0.6, 0.2, 0.7, 0.3, 0.9]. 我们设交叉概率pc=0.5, 对于个体1来说, 当pj>pc时, 子代保留个体1的基因特征, 其余位置上的工件我们根据个体2中这些工件的相对位置来决定相应的次序. 如此我们可以得到这样一个子代个体, 它的2、4、6、8号位置上的工件和个体1一致, 为5、2、8、6; 它的1、3、5、7号位置上的工件和个体2一致, 为3、7、1、4. 最后, 得到一个子代个体[3, 5, 7, 2, 1, 8, 4, 6].
(3)变异
生物在遗传过程中, 难免会发生变异. 遗传算法中同样引入了这种思想. 对于新生成的个体, 设变异概率为pm, 当随机数rand<pm时, 我们随机交换个体中两个位置的工件, 以此作为变异操作.
综上所述, 本文将以上3种遗传操作嵌入到遗传算法中, 并结合上文提出的启发式算法来对并行批处理机调度问题求解, 算法框架如表2所示.
| 表 2 算法框架 |
3 仿真实验设计与分析 3.1 仿真实验设计
本文根据吴愁[6]提出的方法生成随机算例. 算例规模从5个角度进行划分: 工件数量、工件尺寸、加工时间、到达时间和机器数量. 我们考虑了规模分别为10、20、30、40、50、60、70、80、90、100的差异工件算例, 工件尺寸从[1, 10]随机生成, 加工时间从离散均匀随机分布[8, 15]中产生, 机器数量设置为2, 工件的到达从[0,R]中生成, 其中R=
| 表 3 算例规模 |
为了比较算法的性能, 我们将提出的算法和粒子群算法(PSO)作了实验对比, 同时对于每个算例, 首先使用BFLPT-ERTLPT(以下简称BFLPT)启发式算法进行了求解, BFLPT的实验结果也纳入到实验对比当中. 每个算例运行5次取平均值. 所有算法都由Matlab实现, 实验环境为4 G RAM, 2.3 GHz的Windows7电脑.
3.2 实验结果分析实验结果如表4所示, 遗传算法GA与粒子群算法PSO结果中均包含解的质量与运算时间. 而由于BFLPT算法的运算时间很短暂, 不具有对比性, 所以并没有在结果表中列出. 表4中第7列与第8列分别表示的是遗传算法与PSO以及BFLPT算法解的质量对比, 其计算方式为:
| 表 4 结果比较 |
| $ Over\;PSO \!=\! \frac{{avg\;{C_{{\rm{max}}}}\left( {PSO} \right) \!-\! avg\;{C_{{\rm{max}}}}\left( {GA} \right)}}{{avg\;{C_{{\rm{max}}}}\left( {PSO} \right)}}\!*\!100 $ | (16) |
| $ Over\;BFLPT \!=\! \frac{{avg\;{C_{{\rm{max}}}}\left( {BFLPT} \right)\! -\! avg\;{C_{{\rm{max}}}}\left( {GA} \right)}}{{avg\;{C_{{\rm{max}}}}\left( {BFLPT} \right)}}\!*\!100 $ | (17) |
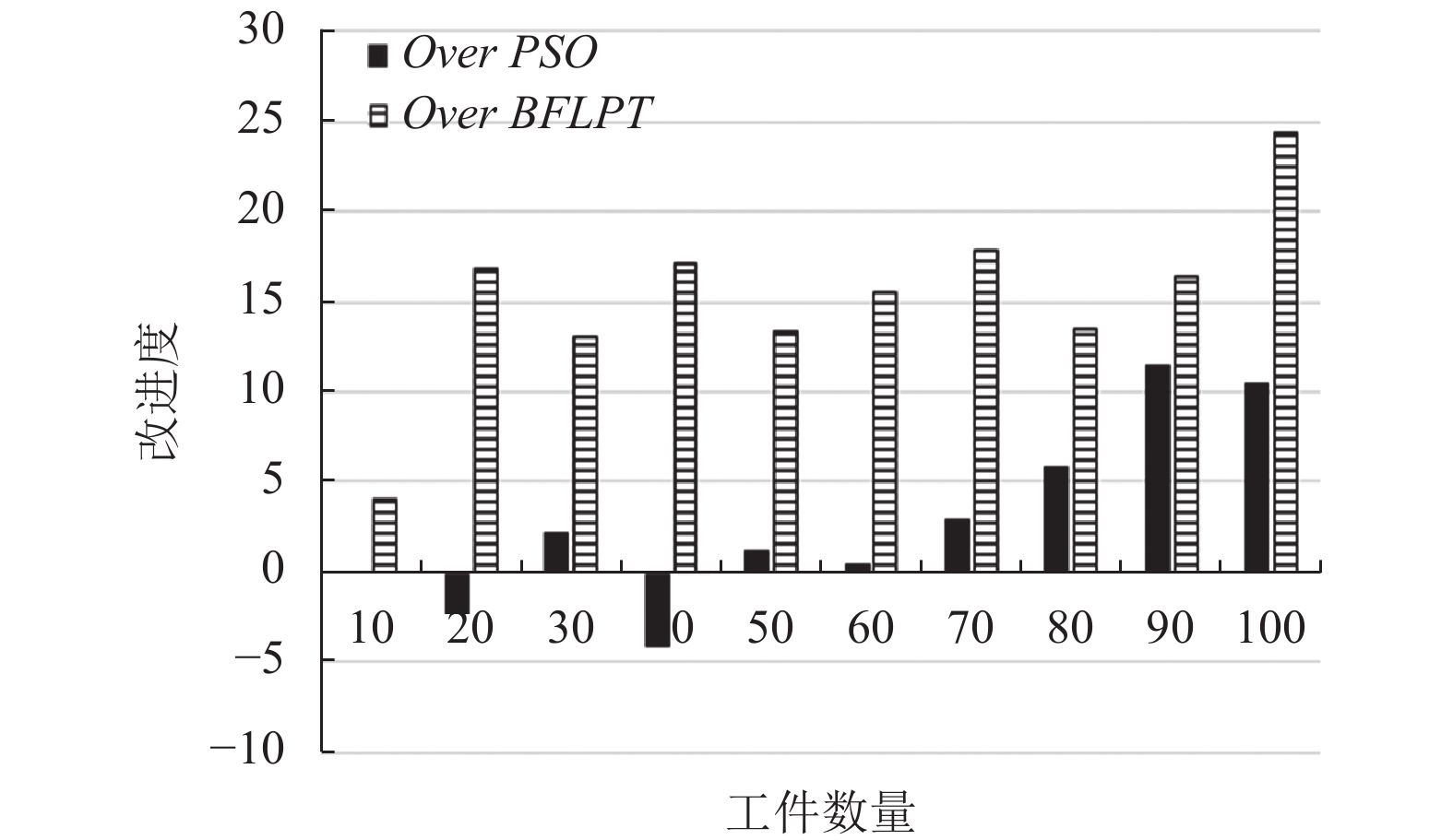
从表4中我们可以看出遗传算法GA的运行时间大多数情况都小于粒子群算法PSO的运行时间. 图3是表4中第2列、第4列与第6列结果对比折线图. 从图3中我们可以清晰的观察到遗传算法GA与其他两种算法解的质量之间的对比情况. 图4是表4中第7列与第8列结果改进柱状图. 从图4中我们可以清晰的观察到遗传算法GA与其他两种算法解的质量改进程度. 如图3与图4所示, 随着工件规模的逐渐增大, 遗传算法GA较之其他两种算法的优势变得十分明显.

|
图 3 不同工件规模下解的质量 |
|
图 4 不同工件规模下解的质量改进 |
4 结论与展望
本文研究了遗传算法在考虑差异工件的并行批处理机调度中的应用问题. 首先提出了一个数学规划模型, 并采用BF规则对工件进行分批, 采用ERT-LPT规则将批分配在机器上加工. 我们提出了一种基于随机浮点数组的交叉操作, 并将其嵌入到遗传算法进行求解. 实验结果表明, 我们提出的算法不论是在解的质量上还是运行时间上, 相比PSO算法都具有很大的优势, 尤其是在大规模工件算例中优势会更加明显.
未来的研究可以考虑更复杂的生产加工模型, 例如多阶段流水车间、柔性车间等; 也可以研究其他的一些优化目标, 例如最大延时时间、延迟工件数等.
| [1] |
Uzsoy R. Scheduling a single batch processing machine with non-identical job sizes. International Journal of Production Research, 1994, 32(7): 1615-1635. DOI:10.1080/00207549408957026 |
| [2] |
Lee CY. Minimizing makespan on a single batch processing machine with dynamic job arrivals. International Journal of Production Research, 1999, 37(1): 219-236. DOI:10.1080/002075499192020 |
| [3] |
Mosheiov G, Oron D. A single machine batch scheduling problem with bounded batch size. European Journal of Operational Research, 2008, 187(3): 1069-1079. DOI:10.1016/j.ejor.2006.01.052 |
| [4] |
Cheng BY, Li K, Chen B. Scheduling a single batch-processing machine with non-identical job sizes in fuzzy environment using an improved ant colony optimization. Journal of Manufacturing Systems, 2010, 29(1): 29-34. DOI:10.1016/j.jmsy.2010.06.007 |
| [5] |
刘娟, 陈华平. 基于云模型的PSO算法求解差异工件单机批调度问题. 计算机系统应用, 2010, 19(2): 164-168. DOI:10.3969/j.issn.1003-3254.2010.02.039 |
| [6] |
吴愁. 遗传算法在考虑能耗的单机批调度中的应用. 计算机系统应用, 2018, 27(8): 138-145. DOI:10.15888/j.cnki.csa.006489 |
| [7] |
Damodaran P, Chang PY. Heuristics to minimize makespan of parallel batch processing machines. The International Journal of Advanced Manufacturing Technology, 2008, 37(9–10): 1005-1013. DOI:10.1007/s00170-007-1042-8 |
| [8] |
郭乘涛, 江志斌. 应用混合蚁群算法求解并行批处理机组批与调度问题. 上海交通大学学报, 2010, 44(8): 1068-1073. |
| [9] |
王庆. 并行多机批调度的问题研究[硕士学位论文]. 北京: 中国矿业大学, 2014.
|
| [10] |
程八一, 黄小曼, 杨艳艳, 等. 差异分批模式下的联合成本优化问题及算法. 管理科学学报, 2016, 19(8): 102-112. DOI:10.3969/j.issn.1007-9807.2016.08.008 |
| [11] |
李国臣, 乔非, 王俊凯, 等. 考虑能耗约束的并行机组批调度. 中南大学学报(自然科学版), 2017, 48(8): 2063-2072. DOI:10.11817/j.issn.1672-7207.2017.08.013 |
| [12] |
张震, 尤凤翔, 赵欣桥. 有模具约束的并行机批量流调度问题研究. 工业工程, 2018, 21(3): 59-64. DOI:10.3969/j.issn.1007-7375.2018.03.007 |
| [13] |
Damodaran P, Manjeshwar PK, Srihari K. Minimizing makespan on a batch-processing machine with non-identical job sizes using genetic algorithms. International Journal of Production Economics, 2006, 103(2): 882-891. DOI:10.1016/j.ijpe.2006.02.010 |
| [14] |
陈成栋. 两阶段流水车间批调度问题的蚁群算法研究[硕士学位论文]. 合肥: 中国科学技术大学, 2012.
|
 2019, Vol. 28
2019, Vol. 28


