支持向量机(Support Vector Machine, SVM)是建立在统计学习理论的VC维理论和结构风险最小原理基础上的, 根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折中, 以期获得最好的推广能力. 目前, 支持向量机分类技术已经广泛应用于机器学习、模式识别、模式分类、计算机视觉、工业工程应用、航空应用等各个领域中, 其分类效果可观, 具有很好的发展前景[1].
SVM最初在线性可分情况下寻求最优分类面, 为解决二类分类问题而提出来的, 不能直接运用于多类分类. 业内专家提出One-Versus-Rest (1-v-r)[2], One-Versus-One (1-v-1)[3], Directed Acyclic Graph (DAG)[4,5], 决策树[6–8]等方法能够将它扩展到多分类问题, 取得较好的分类精度, 但是这些方法尚存在“决策盲区”、“不平衡类”等缺陷, 分类器性能的优劣主要由分类精度和分类速度来确定, 其推广能力受到一定影响. 随着分类问题复杂性的增加, 类别数量、训练样本、特征维数均有所增加, 分类速度也越来越受到重视, 学者不断深入研究改进二叉树算法, 取得了较显著成果, 陈柏志等[9]通过帕累托原则建立类间差异性估计策略对二叉树分类算法进行了改进, 在一定程度上缩减了分类盲区; 赵海洋等[10]则从类型间距方面对BT-SVM的层次结构进行改进, 提高了BT-SVM的分类精度; 权文等[11]为改善分类效果采用了聚类算法对BT-SVM进行了改进, 提高分类精度; 冷强奎等[12]提出通过计算两个距离最远的类的质心获得超平面, 建立混合二叉树结构, 取得较好效果. 因此提高SVM多类分类的快速性和准确性成为机器学习领域研究的热点和难点[13].
本文在对现有主要的SVM多类分类算法作简单介绍和分析的基础上, 提出一种改进的二叉树多类分类算法, 达到又快又好地解决多类分类问题的预期. 在二叉树结构的基础上, 根据训练样本对最优分类超平面的贡献程度, 引入概率计算方法, 为每个二类分类器赋值不同的权重系数, 从而建立一个推广性较高的多类SVM分类模型. 通过采用标准数据集对比分析各种算法的性能, 结果表明基于二叉树的改进分类算法有效, 提高分类精度, 扩大推广能力.
1 支持向量机理论简介[14]Vapnik[15]等人根据统计学习理论提出的一种新的学习方法——支持向量机, 坚持结构风险最小化原则, 尽量提高学习机器的泛化能力, 即由有限的训练集样本得到小的误差能够保证对独立的测试集仍保持小的误差. 在线性可分的情况下, 定义分类超平面f (x)
| $f(x) = W \cdot X + b = \sum\limits_{j = 1}^d {{\omega _j}{x_j} + b} $ | (1) |
当输入的样本值x属于正类时, f (x)≥0; 当输入的样本值x属于负类时, f (x)<0.
| ${y_i}f\left( {{x_i}} \right) = {y_i}\left( {W \cdot {x_i} + b} \right) \ge 0,\;\;i = 1, \cdots ,n$ | (2) |
式中, W是分类面的权系数向量; b为分类的域值. W·X是W和X的内积. 如果要求得到W和b的值, 通过样本与最佳超平面的最近距离为1/‖W‖, W和b的优化条件应是使两类样本到超平面最小的距离之和2/‖W‖为最大. 因此最佳超平面应满足约束:
| ${y_i}\left( {W \cdot {x_i} + b} \right) - 1 \ge 0,\;\;i = 1, \cdots,n$ | (3) |
假设a的最优解为a*, 然后W和b的最优解分别为w*和b*, 这样可以得到:
| $\left\{ \begin{array}{l} {w^ * } = \displaystyle \sum\limits_{i = 1}^n {\alpha _i^ * {y_i} \cdot {x_i}} = \displaystyle \sum\limits_{supportvectors} {\alpha _i^ * {y_i} \cdot {x_i}} \\ {b^ * } = 1 - {w^ * } \cdot {x_i} \\ \end{array} \right.$ | (4) |
式中, sgn(·)代表符号函数, w*表示权值,
| $f\left( x \right) = sgn\left( {\sum\limits_{j = 1}^n {\alpha _i^ * {y_j}{x_j} \cdot x} + {b^ * }} \right)$ | (5) |
核函数是一种特定的高维特征空间的线性学习算法, 实现非线性映射的目的. 典型的核函数有三种: 多项式核函数、径向基核函数、Sigmoid核函数.
SVM在解决小样本、非线性及高维数等模式识别问题中表现出许多特有的优势, 克服人工神经网络学习结构难以确定和存在局部最优等缺点, 这些优势能够被推广应用到分类预测等问题中, 这使它成为机器学习领域的研究热点, 并被成功应用到很多领域. 但是经典的SVM算法只能解决二类分类问题, 如何有效地扩展到多分类问题仍未很好的解决, 特别是标准SVM的判决输出为硬判决, 在多分类中更需要一个具有软判决输出的SVM. 利用标准SVM的判决输出与类后验概率的映射关系[16], 即将SVM的判决输出f (x)通过Sigmoid函数映射到0与1之间, 构造概率输出的数学表达式, 其简化形式如下:
| $p\left( x \right) = p\left( {y = 1/x} \right) = 1/\left\{ {1 + \exp \left[ { - f\left( x \right)} \right]} \right\}$ | (6) |
| $p\left( { - x} \right) = p\left( {y = - 1/x} \right) = \exp \left[ { - f\left( x \right)} \right]/\left\{ {1 + \exp \left[ { - f\left( x \right)} \right]} \right\}$ | (7) |
| $f\left( x \right) = Af + B$ | (8) |
| $f = \sum {{a_i}{y_i}K\left( {{x_i},{x_j}} \right)} + b$ | (9) |
式中, 参数A和B控制Sigmoid函数的形态, A和B是通过最小化已知的训练数据和它们的决策值f的负的对数似然函数得到.
2 多类分类器算法[17]在实际应用中的分类问题都是多类的, 经典SVM无法直接解决, 为将支持向量机技术更好应用于实际中, 目前国内外学者提出了许多途径, 归纳为两类[18]: 一是构造多类分类数学模型, 考虑所有情况, 这种方法在经典SVM分类的基础上, 优化SVM的目标函数和参数, 通过决策实现多类分类. 但是这种方法目标函数的表达式十分复杂, 难于求解, 在工程应用领域很少被采用; 二是按照将多类问题归结为多个两类问题的思路, 通过优化组合多个二分类支持向量机实现多类分类, 即将一个复杂问题转化若干个简单问题, 得到较好推广. 基于第二种算法思想, 经典方法有: One-Versus-Rest (1-v-r), One-Versus-One (1-v-1), Directed Acyclic Graph (DAG), 二叉树等.
2.1 1-v-r算法基本思想[19]: 构造一个二类分类器, 将其中的一类作为一大类, 其余各类作为另外一大类, 分类时把那一类同其他类中分开. 对于N (N≥2)类的分类问题, 需构造N个二类分类器, 采用“比较法”. 对测试样本x进行识别. 将样本输入到已构造的N个二类分类器, 得到相应的N个输出结果, 综合比较这些结果, 明确输出最大的那一类, 其分类器的序号就是样本所属的类别号, 如图1所示.
|
图 1 1-v-r构造示意图 |
决策函数中输出最大值的类别为x的类别, 判定规则的公式
| $\arg \mathop {\max }\limits_{i = 1,2,\cdots,k} \left[ {{{\left( {{w^i}} \right)}^{\rm{T}}}\phi \left( x \right) + {b^i}} \right]$ | (10) |
1-v-r算法的优点是简单、直接. 主要缺点是: 1) 训练样本需要先通过构造的每个二类分类器进行训练; 而已构造的所有二类分类器都要对测试样本进行分类后, 才能确定测试样本的类别, 所以, 一旦训练样本数和类别数较大, 那么训练和测试分类的速度就会比较慢; 2) 假如N类中所有的类型没有测试样本的类型, 这样就找不到正确的类别, 按照“比较法”的方法, 表明N个输出结果中总有输出最大的一个, 就会将本来找不到类别的测试样本误判为N类中的一类, 出现分类的错误.
2.2 1-v-1算法基本思想: 构造N(N≥2)个类别中所有存在的二类分类器, 一共建立N(N–1)/2个, 如图2所示. 采用“投票法”对测试样本进行识别, 将样本输入到已构造的任何一个二类分类器, 当所有的分类器都对测试样本进行分类后, 最后确定哪一类的票数最多, 那么该测试样本就属于这一类别.
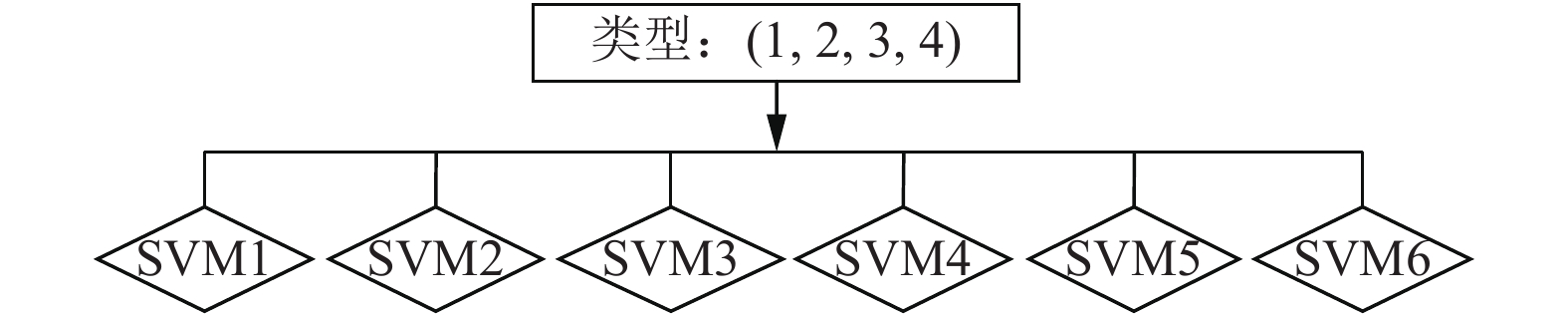
|
图 2 1-v-1构造示意图 |
假设已有第i类和第j类训练样本构造的二类分类器, 算法解决如下优化问题:
| $\left\{\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{w^{ij}},{b^{ij}},{\xi ^{ij}}} \dfrac{1}{2}{{\left( {{w^{ij}}} \right)}^{\rm{T}}}{w^{ij}} + C\displaystyle \sum\limits_t {\xi _j^{ij}} }\\ {\rm{s.t.}}\left\{\begin{array}{*{20}{l}} {{{\left( {{w^{ij}}} \right)}^{\rm{T}}}\phi \left( {{x_i}} \right) + {b^{ij}} \ge 1 - \xi _t^{ij},\;\;{y_t} = i}\\ {{{\left( {{w^{ij}}} \right)}^{\rm{T}}}\phi \left( {{x_i}} \right) + {b^{ij}} \le - 1 + \xi _t^{ij},\;\;{y_t} \ne i}\\ {\xi _t^{ij} \ge 0,\;\;{t = 1,\cdots,n} } \end{array}\right. \end{array}\right.$ | (11) |
构造N(N-1)/2个二类分类器的决策函数, “投票法”判决max((wij)TΦ(xi)+bij), 若属于i类, 则i的票数增加一, 否则j的票数增加一, 哪类统计得票最多, 即为所属类别.
1-v-1算法的优点是每个SVM只考虑两类样本, 易训练, 且其训练速度较“1-v-r算法”方法快, 其分类精度也较“1-v-r算法”方法高. 主要缺点是: 1) 二类分类器的数目N(N–1)/2随着类别数N的增加而增加, 运算量也随之变得很大, 导致训练和测试分类的速度变得非常慢. 2) 测试分类的结果, 一旦出现某两类的得票相同时, 无法找到正确的类别, 可能出现分类的错误. 3) 假如N类中所有的类型没有测试样本的类型, 这样就找不到正确的类别, 按照“投票法”的方法, N类中总有某一类得票最多, 表明N类中总有某一类所得的票数最多, 就会将本来找不到类别的测试样本误分为N类中的一类, 造成分类的错误.
2.3 有向无环图(DAG)算法基本思想[20]: 构造所有的二类分类器, 作为一种双向的有向无环图的节点, 底层的“叶”是由N个类别组成的, 最底层含有N个叶节点, 如图3所示. 按照“自上而下”的原则, 分类时从顶部分类器开始, 依据顶部的分类器分类结果, 判定采用下一层的左节点还是右节点进行分类, 直到底层的某个“叶”为止, 对样本所属的类别进行编号, 对应该“叶”的序号. 采用“排除法”对测试样本进行识别, 将样本输入到已构造的子二类分类器中, 每通过一个, 都能排除掉最不可能的类别, 最终得到底层的某个“叶”所对应的类别.
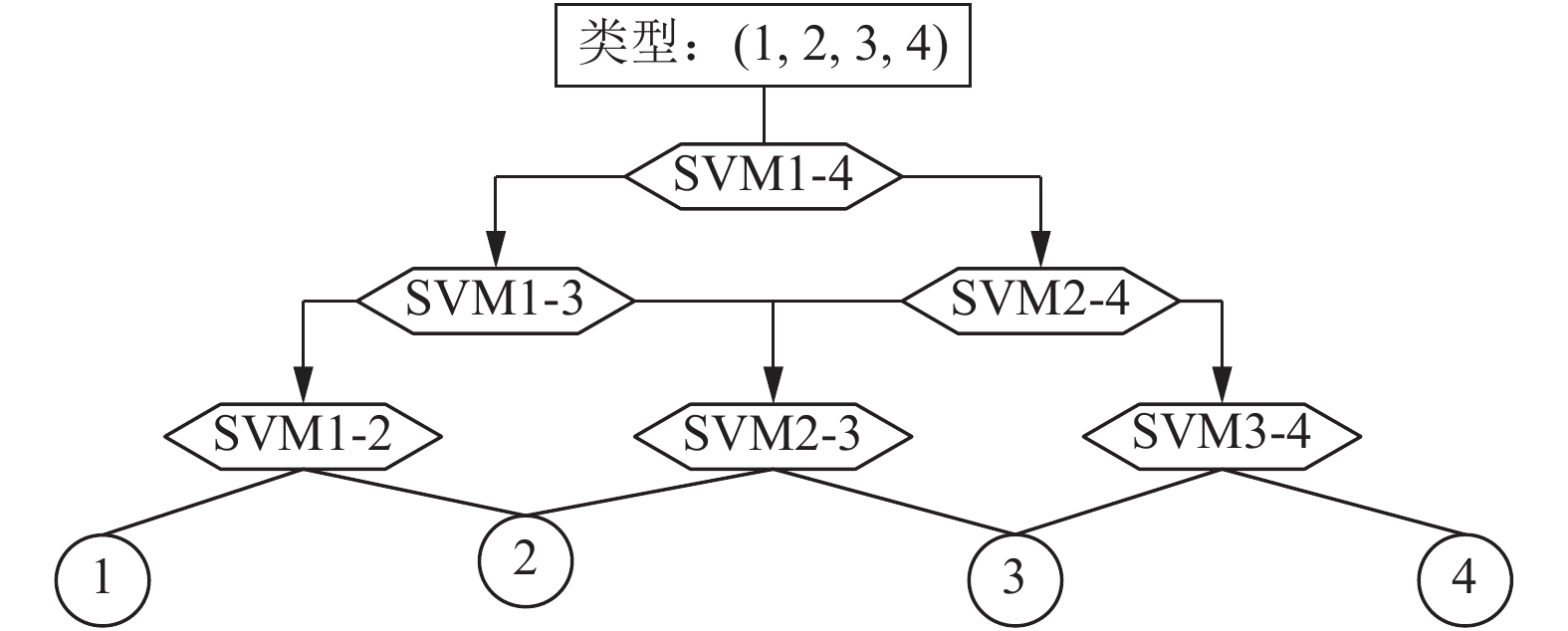
|
图 3 DAG构造示意图 |
DAG算法的优点是在训练阶段, 虽然与1-v-1算法相同, 但在分类阶段时, 仅用N-1个分类器, 分类效率明显高于1-v-1算法和1-v-r算法, 重复训练样本少, 分类精度较高. 采用“排除法”进行分类, 降低误分的可能性. 主要缺点是: DAG结构相对于二叉树, 它具有冗余性, 同一类别的分类个体, 分类路径可能不同, 影响分类精度.
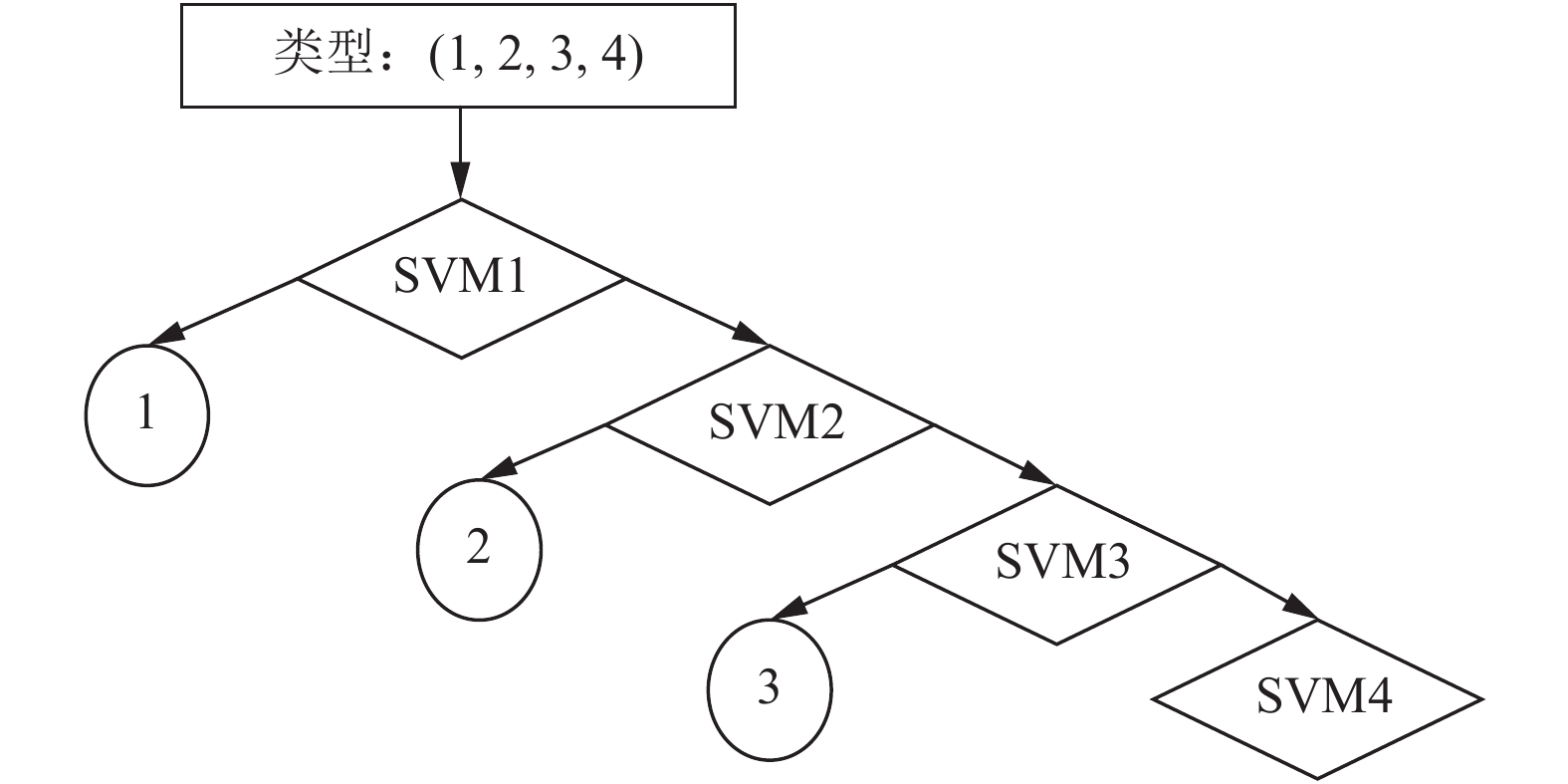
2.4 二叉树分类算法基本思想[21]: 将N(N≥2)类中N/2(或(N+1)/2)类作为一大类, 剩余的类看作另一大类, 建立第一个二类分类器. 然后再分别对那两个多类单独分类, 各取出最相近的N/2-1类作为一大类, 将那N/2类中余下的一类看作另一大类, 再建立一个二类分类器. 往下同理建立二类分类器, 依次往下采取“直接法”直至完全分类, 如图4所示.

|
图 4 完全二叉树构造示意图 |
二叉树分类算法的优点是简单、直观, 重复训练样本少. 对于N类, 测试时仅需建立log2N 二类分类器, 都比前面的三种算法数量少, 克服上面算法存在的无法识别的阴影区域, 而且重复训练的样本量少, 训练和分类的时间可以减少. 主要缺点是初始分类错误具有遗传性, 各子节点的划分方法对结果有较大影响, 在某个节点出现误分类后, 将无法纠正到正确的结果, 因此具有较低的容错率.
以上介绍4种常用的多类分类算法. 其中, 前3种方法在样本数目及类别数目较多时, 训练和分类速度都比较慢, 而且前两种方法还存在不可分区域. 二叉树多类分类方法在识别速度上具有一定的优势, 不过, 二叉树分类器存在着“错误积累”的问题, 对于N类分类问题, 4种算法的对比见表1.
| 表 1 4种算法的对比 |
3 改进的二叉树多类分类算法
在多分类问题中, 二叉树分类算法表现出许多优良的性能, 不仅可以有效解决了不可分问题, 还能减少分类器的数量, 但是也存在较突出问题: 可能会导致“错误累积”现象, 即若在上层节点处分类一旦错误分类, 则这种错误会传递下去, 后续节点将失去分类的意义, 因此二叉树分类算法越上层节点的分类性能对整个分类模型的推广性影响越大. 为了获得最佳的分类效果, 必须根据实际情况来构造二叉树各内节点的最优超平面, 在生成二叉树的过程中, 应该让最易分割的类最早分割出来, 即在二叉树的上层节点处分割. 但考虑到不同的训练样本对最优分类超平面的贡献程度不同, 为综合考虑样本信息, 参考郭亚琴等人[22]提出的样本分布度量方法, 利用类间散布度量与类内散布度量的比值作为样本分布情况的度量, 构造样本间的映射关系. 在二叉树分类的基础上, 构建SVM输出模型, 为二类分类器赋值不同的权重系数, 求得各分类器的可信度. 具体算法流程图如图5所示.
(1) 将训练样本集输入到支持向量机中学习, 求得最优的参数w*、ai*、b*、A、B等, 从而得到式(6), 式(7)中的SVM输出模型Si.
(2) 假设Θ为识别框架, 且
(3) 将训练样本集输入到SVM输出模型进行训练, 求出分类器
(4) 计算测试样本分布情况的度量, 采用类间分布度量与类内分布度量的比值作为分类依据, 将比值相近的作为一大类, 剩余的类看作另一大类, 再根据分类器的可信度, 将属于第i类的样本尽快从样本集中识别出, 属于第i类别的样本标记为正, 而其它样本标记为负. 往下依次, 直至完成分类.
该改进分类算法为解决二叉树的“错误累积”问题, 根据样本对最优分类超平面的贡献程度不同, 通过计算样本分布情况的度量, 利用有限样本数据的分布来对真实分布做近似估计, 同时根据SVM输出模型计算分类器分类可信度, 避免在上层节点处分类出现错误分类, 继续传递错误; 同时搭建较优的二叉树结构, 如图6所示, 能让最易分割的类最早分割出来, 即在二叉树的上层节点处分割, 提高分类效果.

|
图 5 改进分类算法流程图 |

|
图 6 改进二叉树结构示意图 |
4 实验验证
实验仿真采用UCI机器学习公用数据库[23]中Iris和Wine Quality Red数据集的实验数据. 为了验证支持向量机的分类决策性能, 首先利用Iris数据集: 3种不同类型的花(Setosa、Versicolour和Virginica), 以及Iris花的4种特征属性: 花瓣长度、花瓣宽度、萼片长度、萼片宽度, 共150组数据, 每种花50组数据, 每组数据包含4种属性, 在Matlab上进行了仿真试验. 任取部分数据作为实验样本进行测试和分类, 得到Fisher Iris数据集样本分布图和分类结果, 可知支持向量机具有较好的分类性能, 如图7所示.

|
图 7 样本分布图 |
为了测试支持向量机多类分类器的准确性和快速性, 再利用Wine Quality Red数据集: 11种不同质量等级的葡萄酒, 共1599组样本, 每组样本含有11种葡萄酒的有效化学度量值(固定酸度、挥发酸度、柠檬酸、残糖、氯化物、游离二氧化硫、总二氧化硫、密度、pH值、硫酸盐、酒精), 选取与质量等级相关性较大的5种量值(柠檬酸、pH值、酒精度、挥发酸以及硫酸盐)作为特征属性, 支持向量机的结构是5个输入变量, 11个输出变量. 任取150组样本, 作为实验样本, 1/2作为训练样本, 其余1/2作为测试样本, 通过多类分类算法(1-vs-r、1-vs-1、DAG、二叉树及改进的二叉树)对样本进行仿真试验. 分类测试对比结果见表3.
从表2, 表3实验结果来看: 表2是针对类别数为3的多类分类实验结果, 表3是针对类别数为11的多类分类实验结果, 两组实验结果得到类似结果, 说明改进二叉树算法分类方法具有明显的优势.
从时间角度, 时间与决策分类器的数量、求解分类参数的计算量相关, 五种多类分类算法中, 改进的二叉树算法的训练时间稍长于二叉树算法, 由于引入权值计算, 优化问题求解计算量变大, 但是分类器数量最少, 得到分类最优参数后测试时间最短; 而明显短于其它3种算法, 由于搭建分类器的数量少于其它3种算法.
| 表 2 3种类别分类结果 |
| 表 3 11种类别分类结果 |
从分类精度角度, 分类精度与求解决策最优超平面的准确性、是否对样本进行预处理有关, 求解最优分类平面和有针对性地分类可以减少“误分”、“错分”、“不可分”等, 提高了分类精度, 改进的二叉树算法的分类精度最高, 对样本进行预处理, 为分类器赋值不同的权重, 更具针对性, 做到“能分先分, 应分尽分, 难分赋值分”, 分类精度明显高于其它四种算法.
综上, 改进二叉树算法具有较明显的时间优势, 较高的分类精度. 验证了改进二叉树算法分类器的准确性和快速性, 且整体性能稍优于其他4种算法. 如果分类类别多时, 从表1中可知分类器的数量递增, 除二叉树外其他3种算法的分类时间会明显增加, 从表2、表3中可知改进二叉树的分类精度明显高于其他4种算法, 并且类别越多优势更凸显. 因此改进二叉树算法分类方法适用于类别数较多, 分类实时性要求较高的场合.
5 结论本文从支持向量机的基本理论出发, 通过对比分析了4种常见多分类器分类算法的构造原理和特点, 为改进支持向量机的多类分类问题提供依据, 引入二类分类器的权值, 提出基于二叉树的改进分类算法, 实验结果表明该算法可提高多类SVM分类器的效率, 并有助于分类准确率的提升, 使多类支持向量机能够更好地解决工程实际问题. 笔者认为改进二叉树算法的分类器适用于类别数较多, 分类实时性要求较高的场合, 将发挥其优势. 再采用最大化样本类间几何距离的方法划分各类别, 可能会取得更好的效果, 还有待于进一步的研究验证.
| [1] |
刘方园, 王水花, 张煜东. 支持向量机模型与应用综述. 计算机系统应用, 2018, 27(4): 1-9. DOI:10.15888/j.cnki.csa.006273 |
| [2] |
刘雨康, 张正阳, 陈琳琳, 等. 基于KNN算法的改进的一对多SVM多分类器. 计算机工程与应用, 2015, 51(24): 126-131. DOI:10.3778/j.issn.1002-8331.1311-0448 |
| [3] |
单玉刚, 王宏, 董爽. 改进的一对一支持向量机多分类算法. 计算机工程与设计, 2012, 33(5): 1837-1841. DOI:10.3969/j.issn.1000-7024.2012.05.032 |
| [4] |
牛犇, 顾宏斌, 孙瑾, 等. 有向无环图-双支持向量机的多类分类方法. 计算机应用与软件, 2015, 32(11): 167-170, 184. DOI:10.3969/j.issn.1000-386x.2015.11.039 |
| [5] |
汪政, 邵良彬. 多类支持向量机分类算法—DDAG. 计算机系统应用, 2010, 19(7): 87-90. DOI:10.3969/j.issn.1003-3254.2010.07.020 |
| [6] |
李荣雨 程磊. 基于SVM最优决策面的决策树构造. 电子测量与仪器学报, 2016, 30(3): 342-351. |
| [7] |
闫晓静, 于放, 孙咏, 等. 支持向量机决策树在隐患预警模型中的应用. 计算机系统应用, 2017, 26(2): 212-216. DOI:10.15888/j.cnki.csa.005589 |
| [8] |
龙军, 王易, 刘高嵩. 基于二叉树多类支持向量机的文本分类研究. 计算机系统应用, 2009, 18(5): 65-68. DOI:10.3969/j.issn.1003-3254.2009.05.017 |
| [9] |
陈柏志, 石宇强, 詹钧凯, 等. 改进二叉树支持向量机及其TE过程故障诊断. 西南科技大学学报, 2018, 33(2): 101-107. DOI:10.3969/j.issn.1671-8755.2018.02.018 |
| [10] |
赵海洋, 徐敏强, 王金东. 改进二叉树支持向量机及其故障诊断方法研究. 振动工程学报, 2013, 26(5): 764-770. DOI:10.3969/j.issn.1004-4523.2013.05.016 |
| [11] |
权文, 王晓丹. 基于改进FCM聚类的BT-SVM多类分类算法. 微计算机信息, 2009, 25(2–3): 230-232. |
| [12] |
冷强奎, 刘福德, 秦玉平. 一种基于混合二叉树结构的多类支持向量机分类算法. 计算机科学, 2018, 45(5): 220-223, 237. |
| [13] |
薛宁静. 多类支持向量机分类器对比研究. 计算机工程与设计, 2011, 32(5): 1792-1795. |
| [14] |
陈丹玲. 基于小波包和支持向量机的旋转机械故障诊断方法研究[硕士学位论文]. 赣州: 江西理工大学, 2010.
|
| [15] |
Cortes C, Vapnik V. Support- vector network. Machine Learning, 1995, 20(3): 273-297. |
| [16] |
Platt JC. Probabilities for support vector machines and comparisons to regularized likelihood methods. http://research.microsofe.com/~jplatt, [2010-11-15].
|
| [17] |
付静. 面向旋转机械的支持向量机故障智能诊断方法及实验研究[硕士学位论文]. 赣州: 江西理工大学, 2009.
|
| [18] |
宋召青, 陈垚. 基于支持向量机的多类分类算法综述. 海军航空工程学院学报, 2015, 30(5): 442-446. |
| [19] |
Vapnik VN. 统计学习理论的本质. 张学工, 译. 北京: 清华大学出版社, 2000.
|
| [20] |
Platt JC, Cristianini N, Shawe-Taylor JW. Large margin DAGs for multiclass classification. Advances in Neural Information Processing Systems, 2000, 547-553. |
| [21] |
房汉鸣, 税爱社, 汪辉, 等. 支持向量机动态多分类方法. 后勤工程学院学报, 2017, 33(2): 90-96. DOI:10.3969/j.issn.1672-7843.2017.02.015 |
| [22] |
郭亚琴, 王正群. 一种改进的支持向量机多类分类方法. 现代电子技术, 2009, 32(20): 143-146. DOI:10.3969/j.issn.1004-373X.2009.20.046 |
| [23] |
ftp://ftp.ics.uci.edu/.
|
 2019, Vol. 28
2019, Vol. 28

