2. 内蒙古科技大学 信息工程学院, 包头 014010
2. School of Information Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, China
近年来, 由于气候变化、少雨干旱、超载过牧等因素的影响, 内蒙古自治区的部分牧区草原生态环境发生急剧恶化, 甚至严重影响到我国北方和有关邻国的生态安全, 因此, 做好草原生态环境监测工作, 及时掌握草原环境变化, 对合理保护草原以及有效利用草原其意义十分重大.
为了提高环境监测效率, 其监测方法已不再利用单一的监测体系, 而是采用多传感器相互协作方式对环境进行监测, 但是利用多传感器采集到的各种环境参数存在大量冗余, 若将这些数据直接送到监测中心做处理, 不仅增加了数据的传输量, 而且可能导致最终的监测结果存在较大误差. 因此, 学者们将多源数据融合技术应用到环境监测中, 对融合模型和算法进行深入研究. 文献[1]基于自适应加权平均和BP神经网络建立融合模型, 对农田环境进行监测. 但由于BP神经网络易陷入局部最优值, 导致融合结果存在偏差; 文献[2]基于D-S证据理论构建的环境监测模型, 增强了监测指标之间的相关性, 但使用D-S证据理论的难点在于基本概率的分配, 存在较大的主观性, 从而降低监测的准确性; 文献[3]采用AFWDF算法建立融合模型, 对各区域内所有节点采集的数据直接进行加权融合. 但是该模型的运算量较大, 降低了环境监测的效率. 针对上述融合模型的不足之处, 本文建立了一种两级数据融合模型. 通过该模型对多传感器接收的数据进行融合处理, 不仅提高了环境监测的效率, 而且大大提高了准确性.
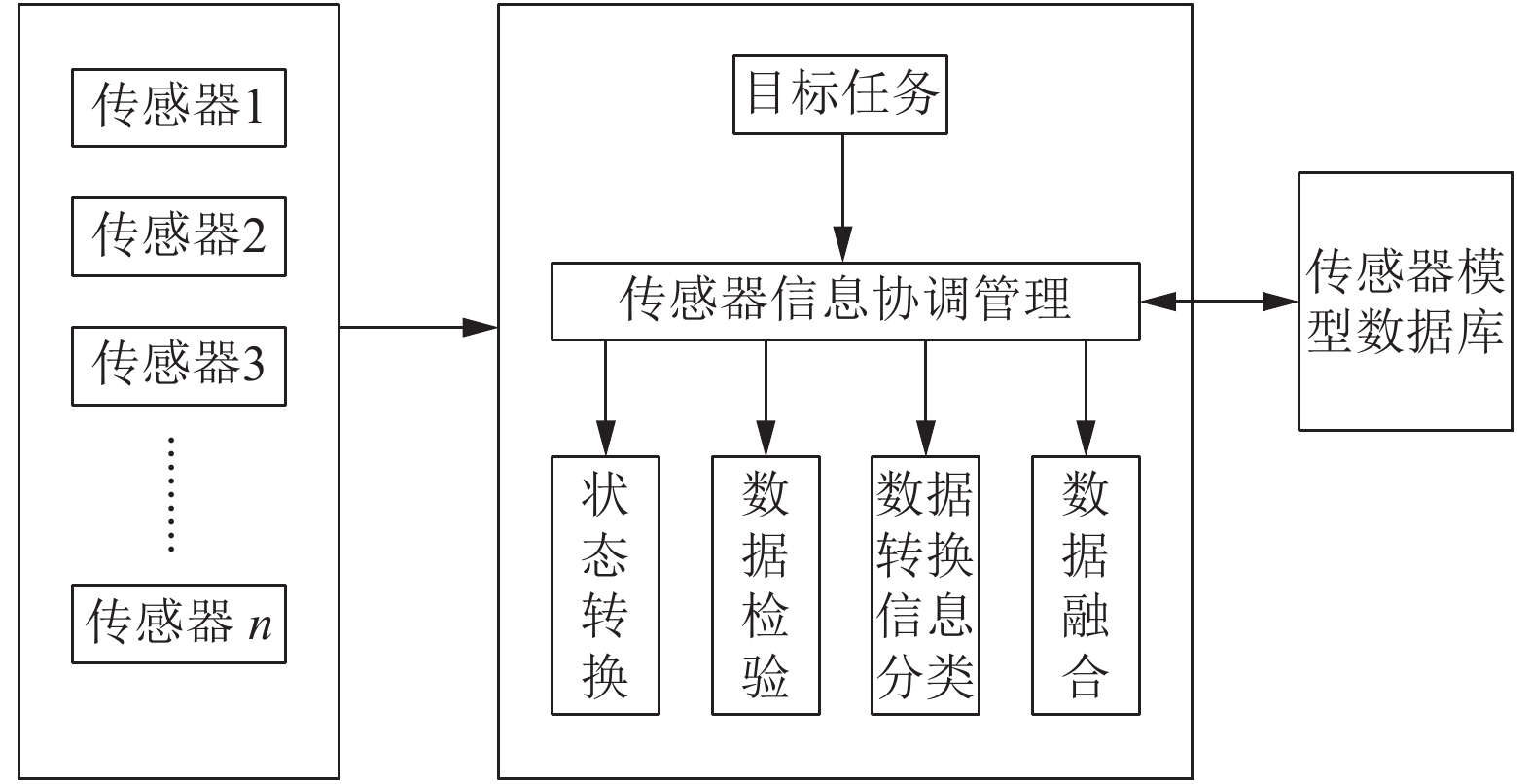
1 多源数据融合技术简介多源数据融合(multi-source data fusion)又称多传感器数据融合, 指的是为了某一目的, 综合处理来自多个传感器的数据, 以期得到既精确又可靠的估计或推理决策[4]. 按照这一定义我们可以进一步明确: 多源数据融合技术是运用计算机技术对来源于各传感器探测的信息, 按照所需达到的目标任务协调和管理传感器信息, 并构建相应的传感器模型, 在此基础上对所收集的传感器数据进行数据状态统一、数据选择剔除、数据分类和数据融合, 以此达到对对象进行综合准确判断的目的[5]. 多传感器数据融合技术流程如图1所示.
数据融合技术的出现和应用起源20世纪70年代[6]. 从20世纪80年代初期到现今为止, 持续的研究热潮使多源数据融合理论和技术得到迅猛发展. 多源数据融合技术的主要特点是它可以依靠一定的标准来综合分析不同时间和空间的数据, 以获得比单传感器更准确的类别或者状态检测. 如今该技术在众多领域得到广泛应用, 原因在于该技术具有较高的精确度和抗干扰能力.
|
图 1 多传感器数据融合技术流程 |
把多源数据融合技术应用到各种领域, 对同类传感器来说, 它不仅可以获得较全面准确的信息, 还能克服因信息的冗余性造成输出结果不确定性的缺点, 提高其可信度. 同样地对于异类传感器, 数据融合技术可以互补不同传感器测得的数据, 而相互补充的信息既补偿了单个传感器测量的不确定性, 又解决了测量范围局限性的问题, 因此应用多源数据融合技术对增加系统的可靠性起到了很大的帮助.
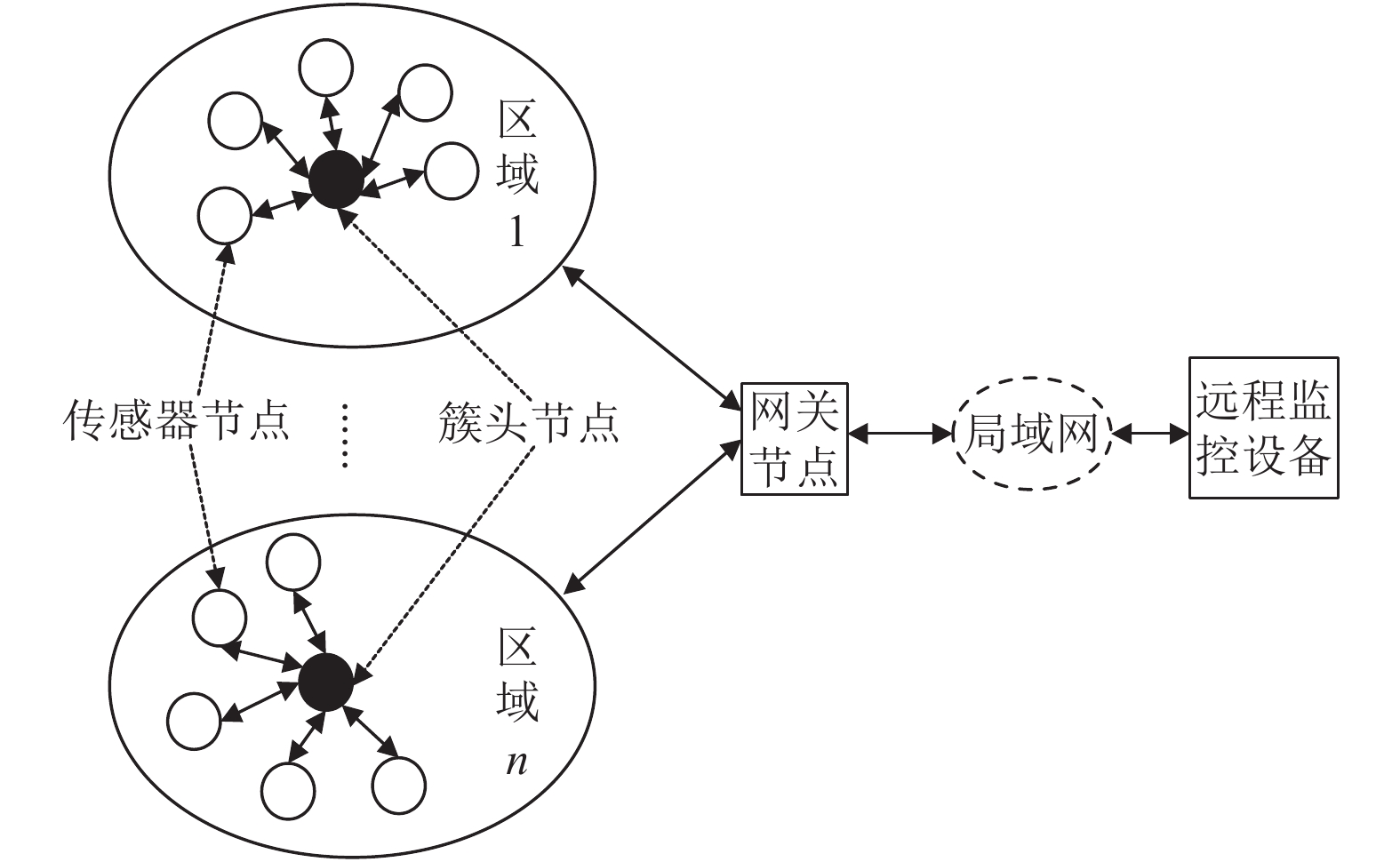
2 草原环境监测的数据融合模型构建由于草原地域广阔, 需要划分区域布置传感器, 每个区域内都布置若干个传感器节点, 然后根据LEACH协议在各区域按照一定规则选取一个簇头节点, 这便形成一个分簇结构[7,8]. 其网络拓扑图如图2所示. 其中传感器节点主要负责采集各类环境参数数据, 簇头节点则负责接收各区域内传感器节点送来的数据. 簇头节点在收到各传感器节点传来的数据后执行一级融合, 然后将一级融合结果发送给网关节点. 网关节点负责接收不同区域传来的数据, 在接收到各区域传来的数据后进行二级融合, 通过对融合结果的综合分析得到最终的环境状况.
|
图 2 草原环境监测网络拓扑结构 |
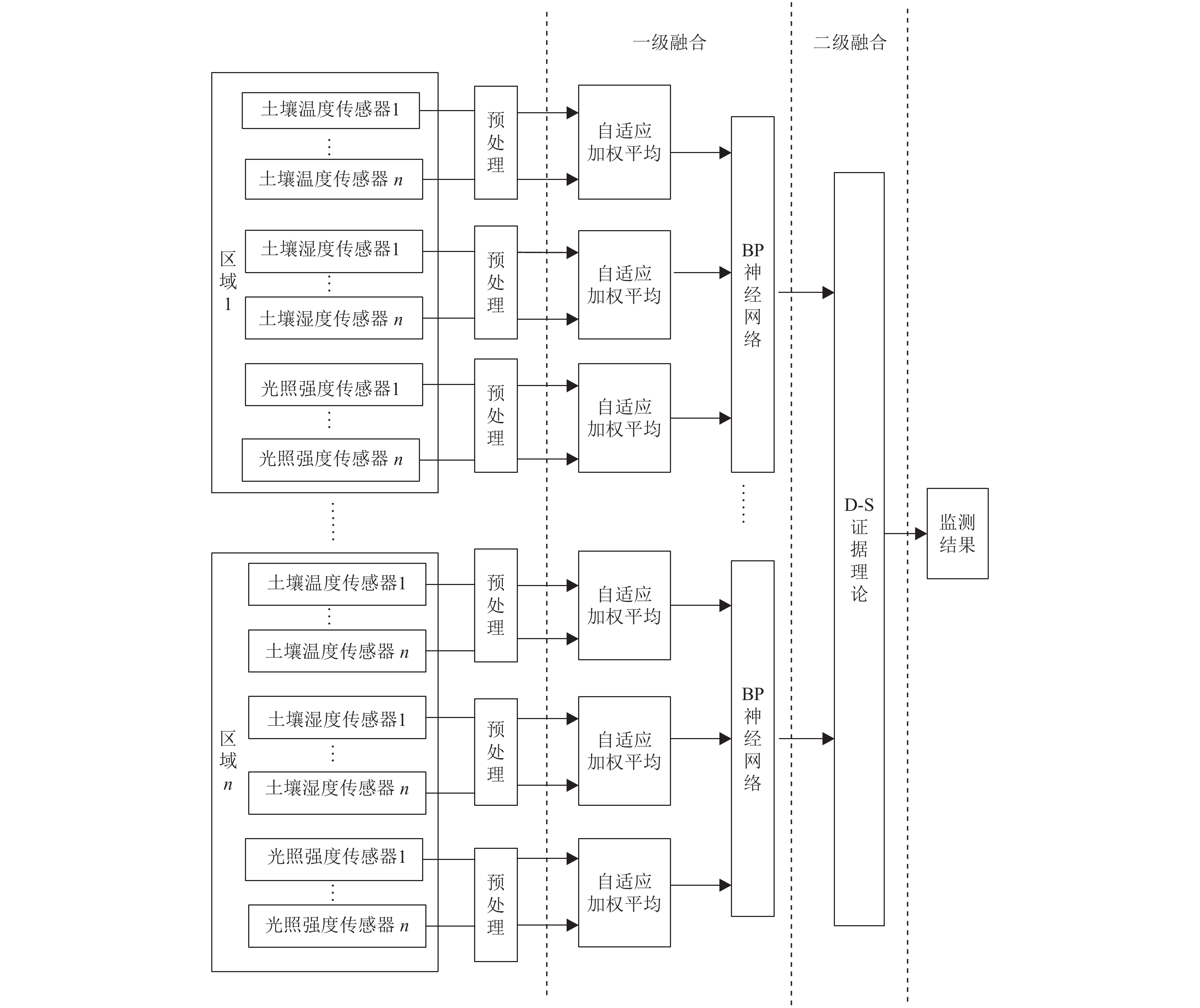
本文以监测土壤温度、土壤湿度和光照强度3个环境参数为例, 设计两级数据融合模型如图3所示. 当簇头节点接收到该区域中传感器采集的数据之后, 首先对该区域内的同类传感器数据利用自适应加权平均法来融合; 其次, 采用BP神经网络方法对各区域进行局部融合处理, 即把各区域的异类传感器数据进行融合. 然后将一级融合结果发送到网关节点进行二级融合, 二级融合采用D-S证据理论对BP神经网络局部融合的结果进行决策级融合, 从而整体判断草原环境状况.
|
图 3 草原环境监测多源数据融合模型示意图 |
数据预处理: 在传感器采集的数据中, 可能有异常数据存在, 所以在融合前有必要进行预处理. 在这些异常数据中, 一种称为有效异常数据, 主要是因为周围环境存在隐患引起的; 另一种是节点故障等非正常因素导致采集到的无效异常数据, 这些无效异常数据会影响最终的融合结果, 因此需要判断传感器测量数据的有效性[9]. 在本文中, 判断采集数据的有效性方法是群体支持度的思想, 以此剔除无效的异常数据, 其不参与融合.
数据融合: 由于每个区域内各传感器的测量精度不同, 若直接将传感器接收的数据融合, 计算量较大. 因此, 首先利用自适应加权平均法对区域内多个同类传感器预处理后数据进行融合, 自适应地根据均方误差最小的方法寻找对应的权值, 将预处理后的数据乘以权值后相加得到对各区域内同类传感器融合. 然后利用BP神经网络对各区域异质传感器数据进行融合, 输出为各区域的环境状况. 经一级融合得到的融合结果仅能够反应该区域内的环境状况, 具有一定的不确定性, 因此需要进行二级融合整体判断草原环境状况, 即归一化处理各区域BP神经网络输出值, 以此作为各区域焦点元素的基本概率分配. 最后再利用D-S证据理论进行综合考虑, 得到最终判断.
2.1 数据预处理在数据融合过程中, 无效异常数据会导致最终融合结果不准确. 因此, 应剔除无效异常数据. 为了准确判断异常数据的有效性, 本文引入群体支持度的思想.
用群体支持度来判断异常数据有效性的方法如下[9]: 在所有传感器节点数据中, 都有一个支持度, 而支持度所反映的是该区域内临近节点对异常数据有效性的支持. 假设某区域内测量土壤温度的传感器有若干个, 其中节点i的测量值记作
为了证明各传感器采集数据的相关支持度, 采用支持度函数
(1)
(2)
(3)若
描述支持度函数通常采用高斯函数, 但高斯型支持函数需要执行指数运算, 这将占用节点大量的硬件资源, 并不适用于资源有限的传感器网络. 因此, 本文提出了一种改进型支持度函数, 以提高数据融合的精确度. 如式(1)所示:
| $\sup (m, \;n) = SN(m,\; n, \;K,\; \beta ) = K \times {\left(1 + {(a - b)^6}\right)^{ - 1}}$ | (1) |
式中,
设某区域内采集土壤温度的传感器节点有n个, 通过式(1) 计算支持度矩阵.
| $S = \left[ {\begin{array}{*{20}{c}} {{s_{11}}}&{{s_{12}}}& \cdots &{{s_{1n}}} \\ {{s_{21}}}&{{s_{22}}}& \cdots &{{s_{2n}}} \\ \vdots & \vdots & \vdots & \vdots \\ {s{}_{n1}}&{{s_{n2}}}& \cdots &{{s_{nn}}} \end{array}} \right]$ | (2) |
则其他传感器节点对传感器节点
| ${s_i} = \sum\limits_{j = 1}^n {{s_{ij}}} $ | (3) |
若
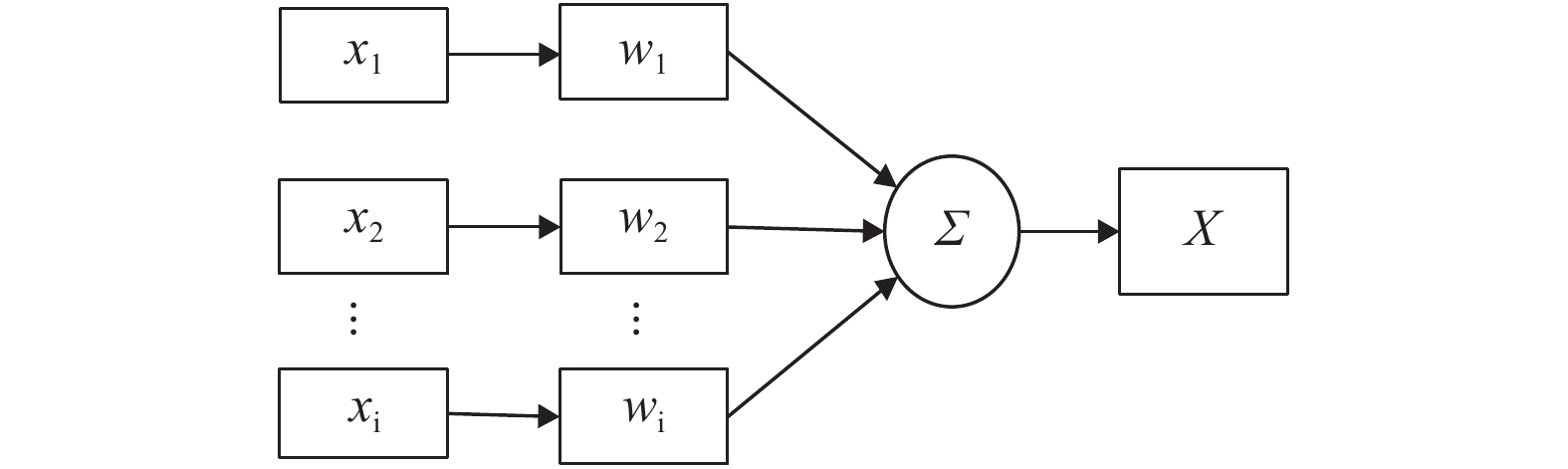
本文首先将各区域内经预处理后的同类传感器数据进行融合, 采用的是自适应加权平均法. 由于不同传感器的权重不同, 因此根据均方误差最小理论, 自适应寻找各传感器对应的权值
|
图 4 自适应加权融合算法模型示意图 |
假设某一区域内用到n个土壤温度传感器, 每个传感器的方差分别为
| $\mathop X\limits^ - = \sum\limits_{i = 1}^n {{w_i}{x_i}} $ | (4) |
| $\sum\limits_{i = 1}^{{n}} {{w_i} = 1} $ | (5) |
其中, 均方误差如式(6)所示:
| $\begin{aligned} {\sigma ^2} & = {{E}}\left[{(x - {\bar X} )^2}\right]\\ & = E\left[\sum\limits_{i = 1}^n {{w_i}^2{{(x - {x_i})}^2}}\right. \left.{+ 2\sum {{w_i}{w_j}(x - {x_i})(x - {x_j})} } \right] \end{aligned}$ | (6) |
由于各传感器安装在草原的不同位置并且距离足够远, 因此可近似认为各传感器数据相互独立, 所以有:
| ${{E}}\left[(x - {x_i})(x - {x_j})\right] = 0\;(i \ne j)$ | (7) |
| ${\sigma ^2} = {{E}}\left[\sum\limits_{i = 1}^n {w_i^2{{(x - {x_i})}^2}} \right] = \sum\limits_{i = 1}^n {w_i^2\sigma _i^2} $ | (8) |
当均方误差最小时, 各土壤温度传感器所对应的权值为:
| ${{w}_i} = 1/\sigma _i^2\sum\limits_{i = 1}^n {\frac{1}{{\sigma _i^2}}} $ | (9) |
类似地, 可获得该区域内土壤湿度传感器和光照强度传感器在剔除无效异常数据后的一级融合值.
2.2.2 BP神经网络融合方法在本文中, 采用BP神经网络方法对各区域内异类传感器数据进行局部融合. 各区域自适应加权平均融合后得到的各环境参数融合值作为BP神经网络的输入, 利用BP神经网络分别对各区域的异类传感器数据做融合处理, 得到该区域环境状况判断. 其中具体融合方法如下:
(1) 首先预处理这3种类型传感器的数据;
(2) 经预处理后, 分别对各环境参数进行特征提取;
(3) 归一化处理各特征信号, 提供统一的形式以供神经网络输入;
(4) 开始进行BP神经网络训练. 将样本数据送入BP神经网络中, 训练到满足要求为止. 然后将训练好的网络作为已知网络, 把归一化处理后的监测数据送入该神经网络中, 此时神经网络的输出即为该区域的环境状况.
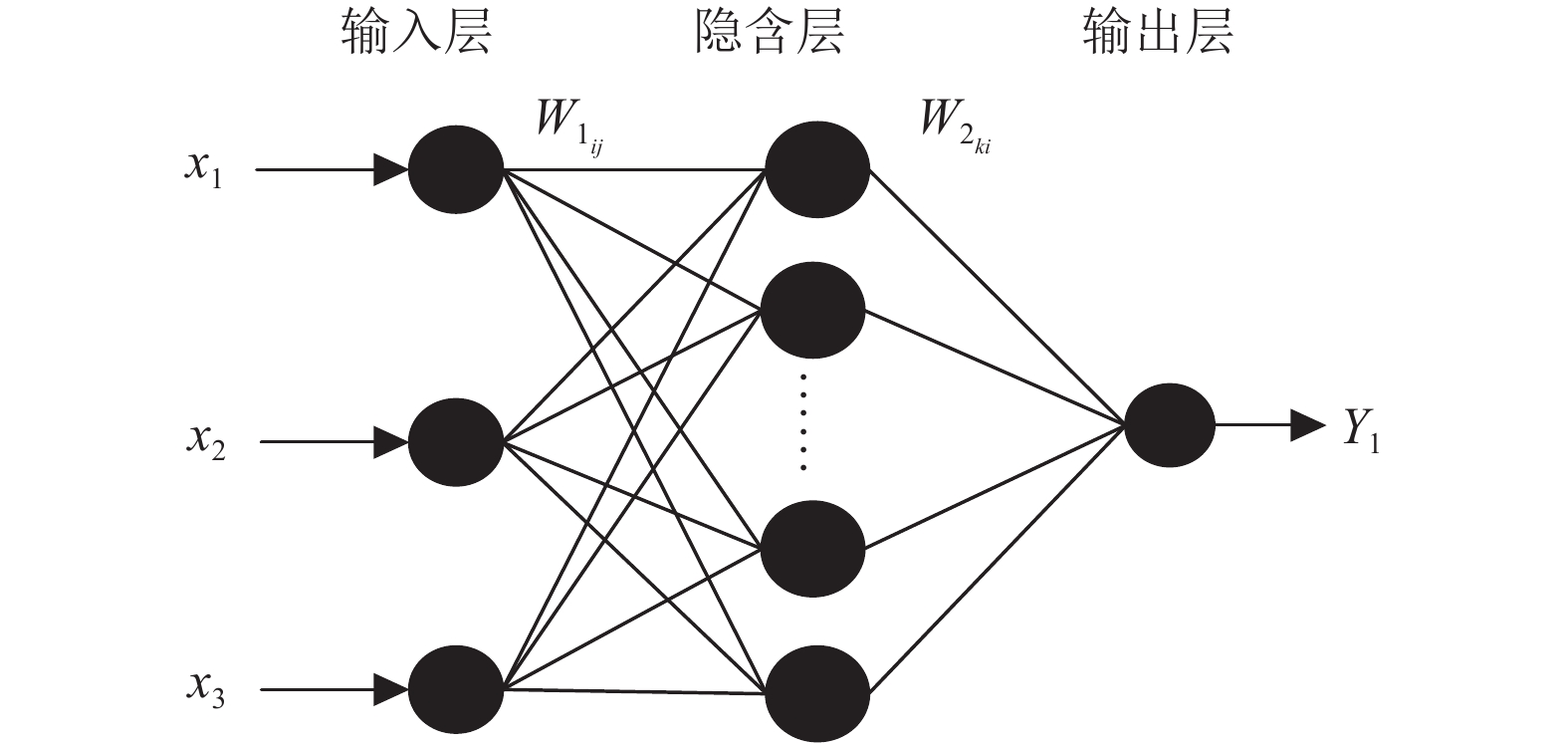
根据草原环境监测的实际情况, 本文设计的BP神经网络模型如图5所示. 其中各参量意义如下: 输入向量
|
图 5 BP神经网络模型 |
根据选择的三个环境参数并经过反复训练, BP神经网络的各层参数设置如下: 其中输入层神经元的个数, 是根据输入信号的维数确定的, 本文中选取3个环境参数作为输入量, 即为土壤温度、土壤湿度和光照强度; 隐含层神经元的个数的选取, 一般是由经验公式(10) 计算出隐含层节点数的区域范围, 并通过实验进行确定, 直到网络输出误差值最小为止[11].
| ${{p}} = \sqrt {{{m}} + {{n}}} + {{a}}$ | (10) |
式中, p为隐含层节点数; n为输入层节点数; m为输出层节点数; a为[1, 10]之间的常数. 由经验公式(10), 可以得到隐含层节点数范围在[2, 12]之间. 通过实验结果发现当隐含层节点数为6时, 网络误差较小, 因此本文将隐含层节点数设定为6个. 输出层设置神经元节点个数为1, 输出的是对各区域的环境状况初级判断.
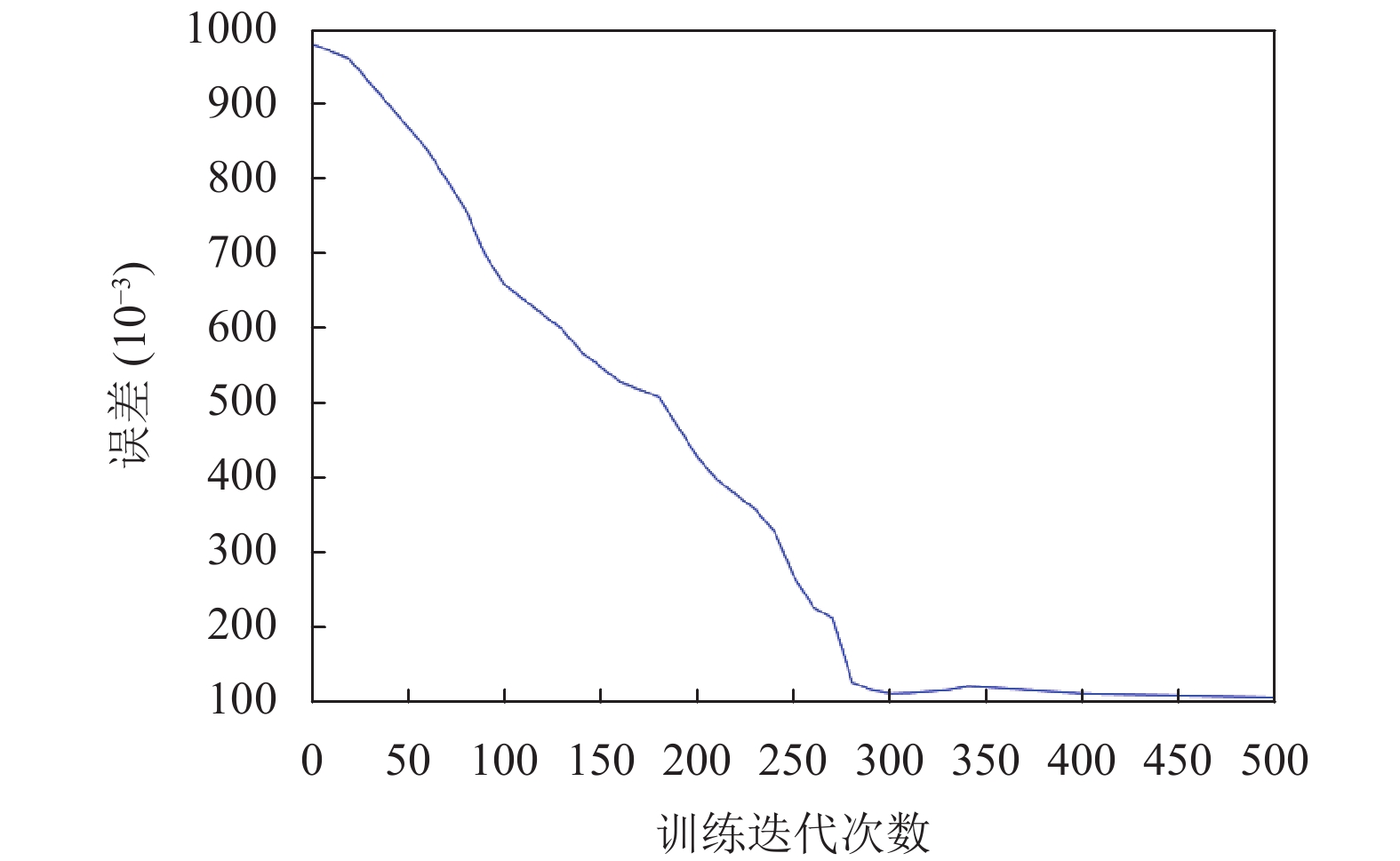
在BP神经网络各层节点数设计完成后, 开始对BP神经网络进行训练. 本次训练采集1200组数据作为样本数据, 然后利用图3所示的BP神经网络结构, 使用MATLAB工具箱建立BP神经网络. 在考虑收敛精度与收敛速度最佳的情况下, 采用logsig函数作为激活函数将网络输出限定到(0, 1)区间上, 训练函数使用trainlm函数, 学习函数使用learnpbm函数, 取目标误差值
|
图 6 BP神经网络训练曲线 |
由图6可以看出, 在训练300次后趋于稳定. 若训练误差要求越来越小, 则训练结果更接近实验期望值. 因此, 直到网络误差满足
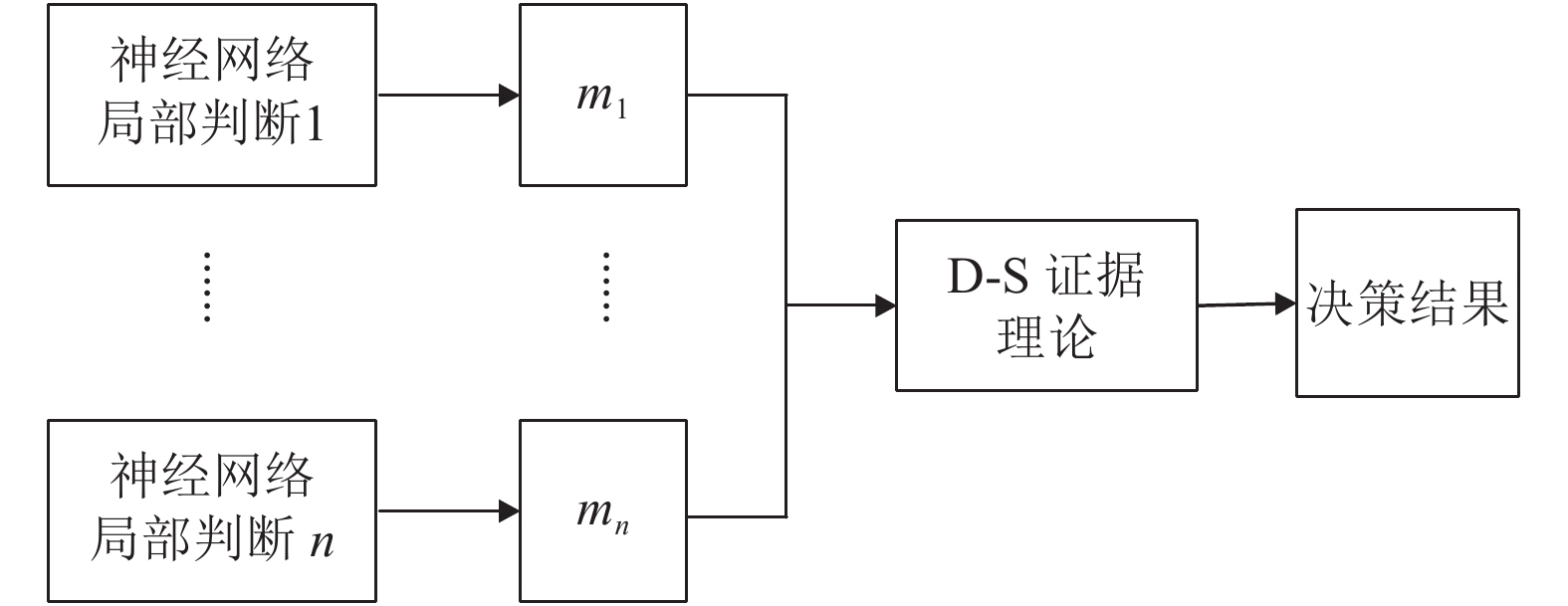
为了增强草原环境监测的精度, 采用D-S证据理论进行全局融合. BP神经网络局部融合的缺点在于其结果具有不确定性, 而D-S证据理论恰为解决不确定性问题提供一种有效的方法. 本文经过一级融合后, 可得到对各区域的局部判断. 然后归一化处理各区域BP神经网络的输出值, 再利用D-S证据理论进行决策级融合. 具体方法如下:
假设将一处草地分为n个区域, 其中区域1经BP局部融合后的结果记为
|
图 7 D-S证据理论融合模型 |
在问题域中, 任意命题A均属于幂集
| ${{m}}(\phi) = 0, \sum\limits_{{{A}} \subseteq \Omega } {{{m}}({{A}})} = 1$ | (11) |
式中,
将D-S证据理论中的信任函数Bel及似然函数Pl, 定义如下:
| ${{Bel(A)}} = \sum\limits_{B \subseteq A} {m(B)} $ | (12) |
| ${{Pl}}({{A}}) = 1{{ - Bel}}({{A}}) = \sum\limits_{{{B}} \cap {{A}} \ne \Theta } {{{m}}({{B}})} $ | (13) |
对所有满足条件
例如, 将整个草原监测区域划分为n个区域, n个区域对应m个证据, 分别记为
| ${{m}}({{A}}) = \frac{1}{{1 - k}}\sum\limits_{B \cap {{A}} = {{A}}} {\prod\limits_{{{j}} = 1}^{{n}} {{{{m}}_{{j}}}({{{A}}_{{i}}})} } $ | (14) |
式中,
由于D-S证据理论基本概率分配函数必须满足条件
利用D-S进行二级融合的运算复杂度主要取决于所划分区域的个数, 因为n个区域所对应的是n条证据体. 并且本文在使用D-S证据理论的过程中, 不仅解决BP神经网络输出的不确定性, 同时借助mass函数, 设置置信区间, 保证了各子集数据的有效性.
3 仿真实验与结果分析为了验证该两级融合模型的有效性, 实验选取某一草坪并将其划分为5个区域, 分别标记为A, B, C, D, E, 每个区域内均布置若干个土壤温度传感器、土壤湿度传感器、光照强度传感器节点和一个簇头节点. 选用Matlab2016仿真工具进行模拟实验. 在每个区域3种传感器分别采集的200个样本数据, 为了实验具有普遍适用性, 每次仿真实验在各类传感器采集的数据中随机抽取180个样本进行模拟, 剩余的20个样本作为模型的测试集.
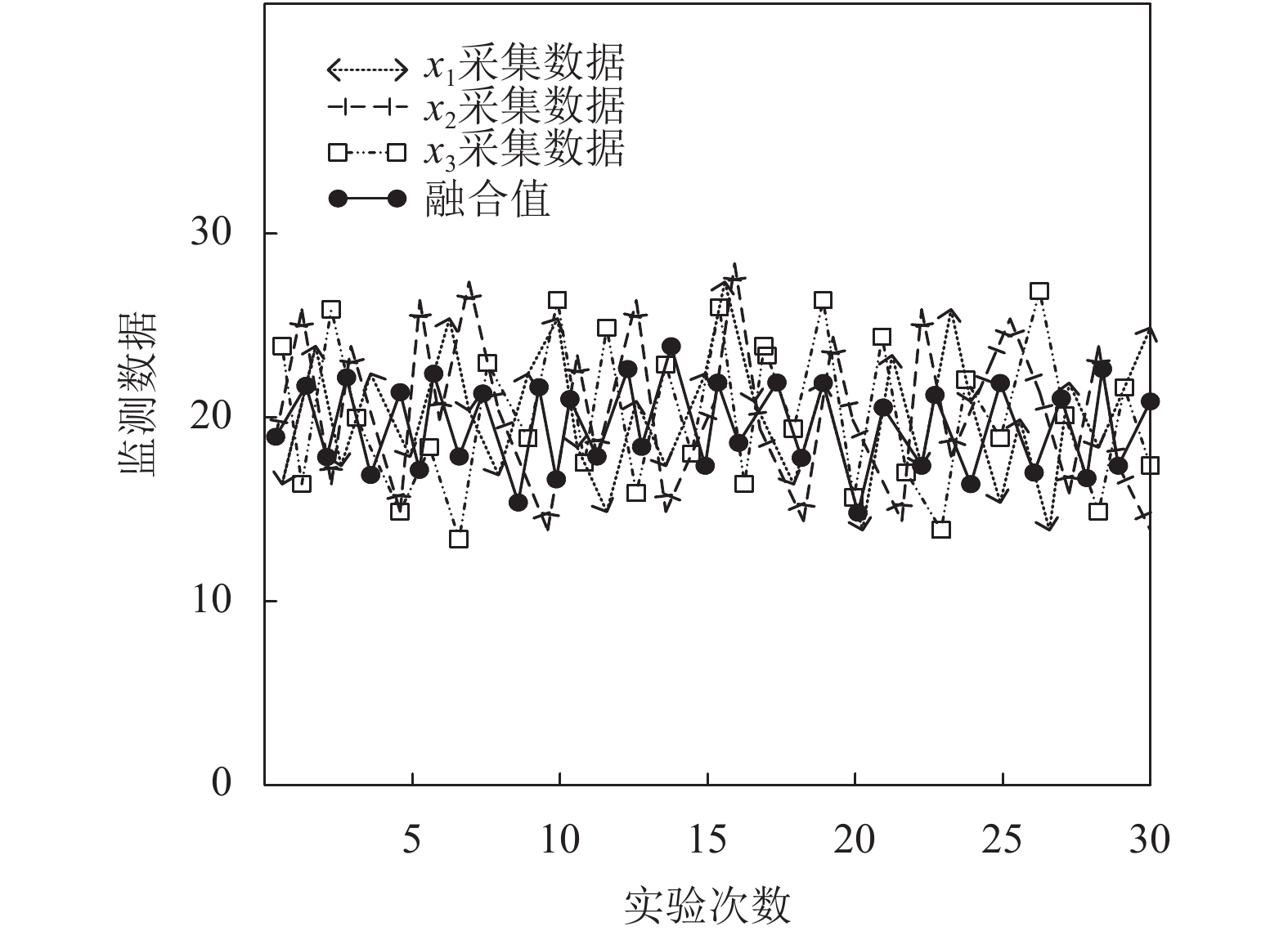
首先利用自适应加权平均法得到各区域内3个环境参数的融合值. 例如A区域内有3个土壤温度传感器采集的数据进行实验, 3个传感器节点分别标记为
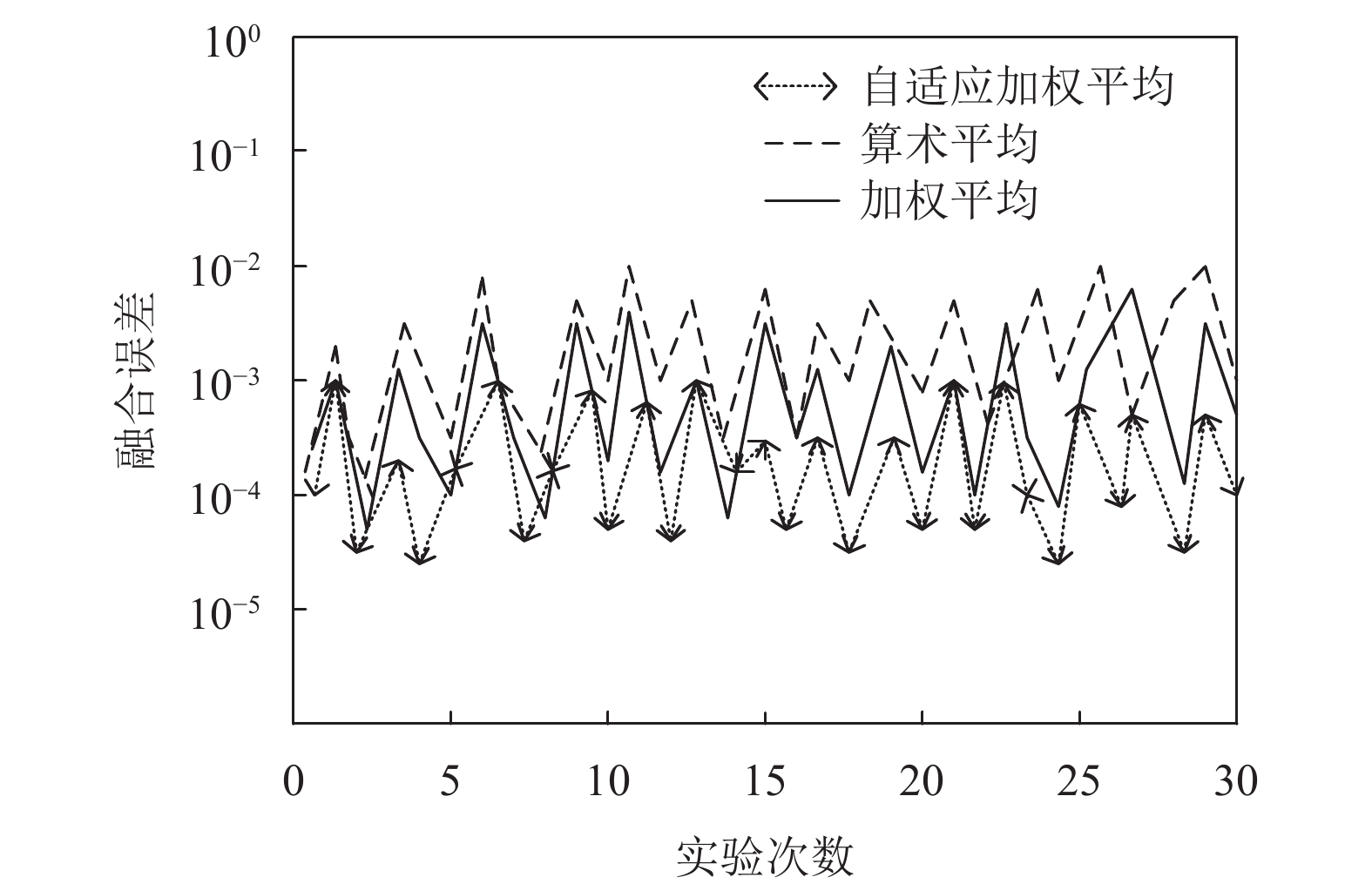
通过上述实验可以看出, 存在一些节点采集的数据波动较大. 但通过自适应加权平均法对同类传感器数据融合后, 这些波动较大的数据, 对实验结果的影响并不大. 为了进一步体现自适应加权平均的准确性及有效性, 分别对自适应加权平均、算术平均[15]和加权平均3种方法的融合误差进行对比, 图9所示为3种方法的融合误差.
|
图 8 A区域3个土壤温度传感器采集数据 |
|
图 9 三种方法的融合误差对比 |
经过30次实验可以看出, 算术平均法的融合误差最大精度最低, 而自适应加权平均法的融合误差最小精度最高. 由此说明了自适应加权平均法的有效性.
根据该两级融合模型功能结构以及采集的实验数据形式, 选用平均绝对百分比误差和相关系数, 对二级融合模型的性能进行综合评价. 计算公式如下:
平均绝对百分比误差:
| $MAPE = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{|f({x_i}) - {y_i}|}}{{{y_i}}}} $ |
相关系数:
| $\lambda = \frac{{{{\left(n\displaystyle \sum\limits_{i = 1}^n {f({x_i}){y_i}} - \displaystyle \sum\limits_{i = 1}^n {f({x_i})\displaystyle \sum\limits_{i = 1}^n {{y_i}} } \right)}^2}}}{{\left(n\displaystyle \sum\limits_{i = 1}^n {f{{({x_i})}^2}} - {{\left(\displaystyle \sum\limits_{i = 1}^n {f({x_i})} \right)}^2}\right)\left(n\displaystyle \sum\limits_{i = 1}^n {{y_i}^2 - {{\left(\displaystyle \sum\limits_{i = 1}^n {{y_i}} \right)}^2}} \right)}}$ |
其中,
|
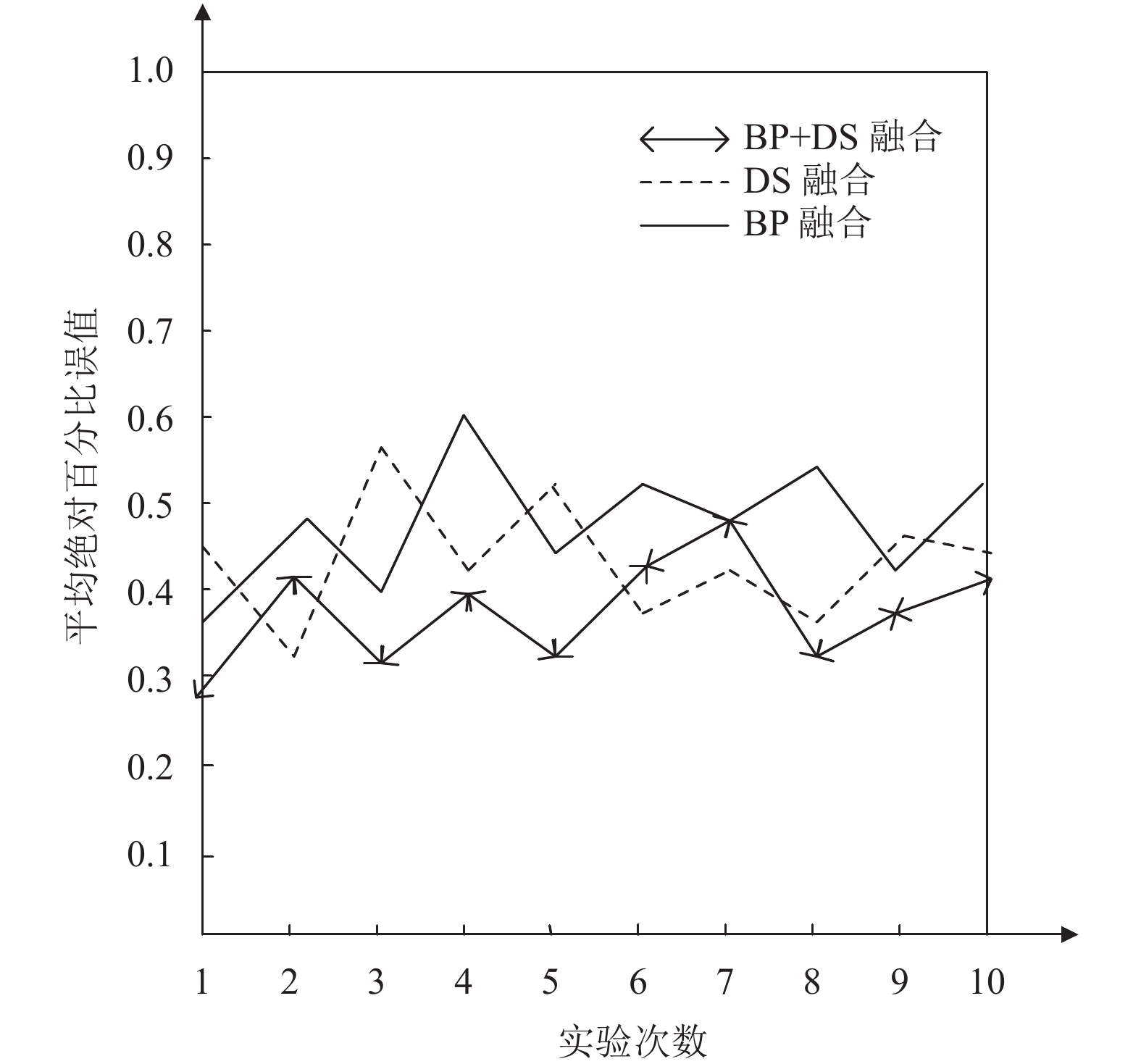
图 10 平均绝对百分比误差对比图 |
|
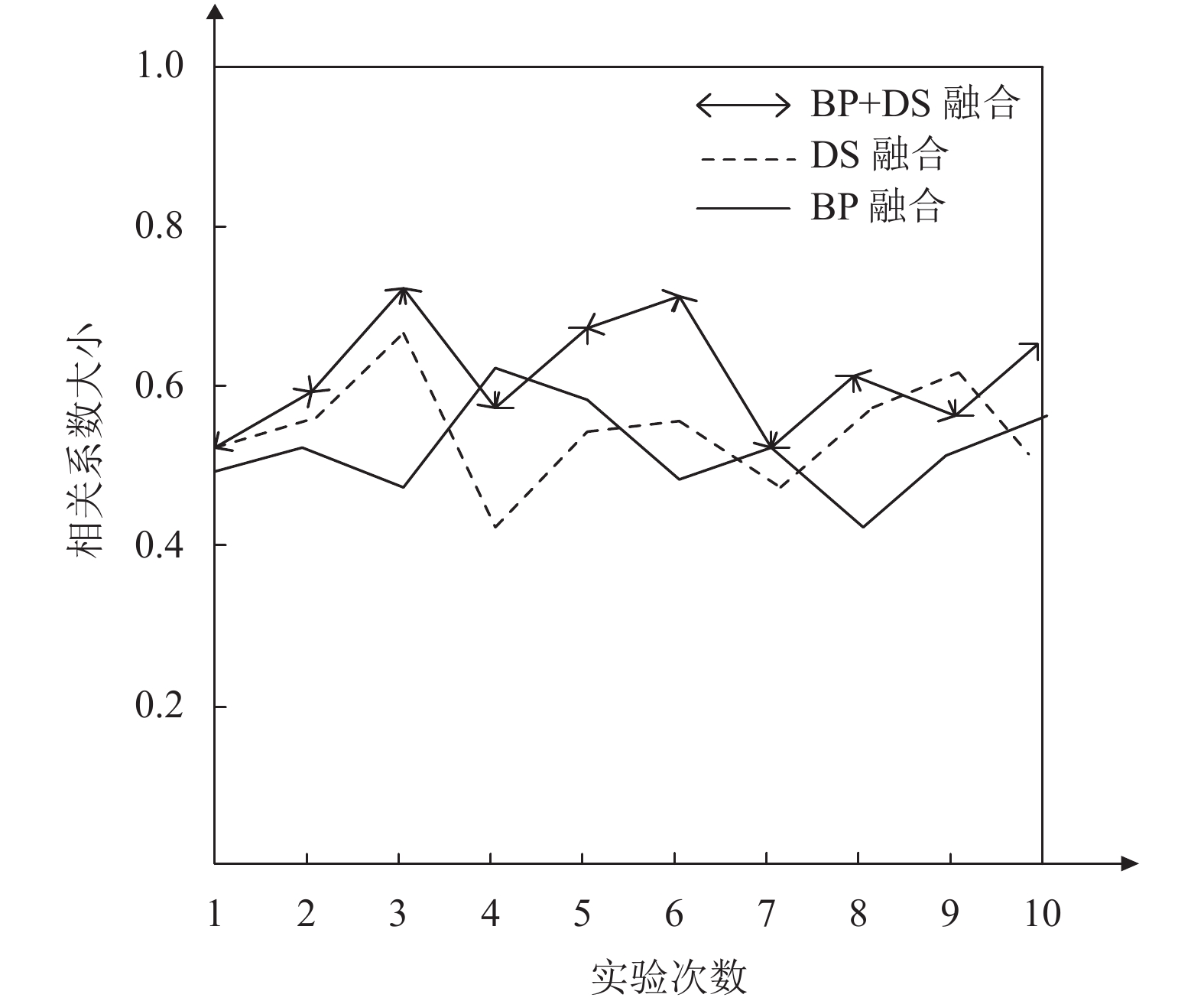
图 11 相关系数对比图 |
通过图10可以看出, 使用BP神经网络融合的绝对百分比误差普遍大于使用D-S证据理论融合的均方误差. 但将二者结合使用, 发现其远小于单独使用这两种融合方法. 根据图11所示的结果分析, BP神经网络和D-S证据理论结合使用的相关性系数更接近1, 其中大多数在0.5以上. 由此说明将BP神经网络和D-S证据理论结合进行融合的系统性能更好. 通过实验验证了该两级融合模型的有效性, 同时该模型提高了系统的精度, 表明将多个传感器获得的数据进行融合的结果更加符合实际情况.
4 结束语本文根据草原生态环境的是实际情况, 建立了两级融合模型. 由于传感器故障等原因导致采集的数据中会存在无效异常数据, 因此融合前首先利用群体支持度的方法剔除无效异常数据, 保留有效异常数据. 然后先对各区域同类传感器采用自适应加权平均法进行融合, 再利用BP神经网络对异类传感器数据融合, 此时输出为各区域环境状况. 因经BP神经网络输出的结果存在不确定性, 本文针对一级融合结果, 采用D-S证据理论进行决策级融合. 将BP神经网络自适应性的特点与D-S证据理论基本概率分配问题互补, 即把BP神经网络的输出值进行归一化处理, 以此作为基本概率分配值, 再利用D-S证据理论进行决策判断. 本文的模型致力于解决多源传感器在草原环境中采集参数数据过程中, 可能出现的不确定性, 最后通过模型的性能评价, 证明了该模型有一定的可靠性.
| [1] |
孙玉文. 基于无线传感器网络的农田环境监测系统研究与实现[博士学位论文]. 南京: 南京农业大学, 2013.
|
| [2] |
刘卫萍, 王宁, 周晓磊, 等. 数据融合技术在环境监测领域的应用. 计算机系统应用, 2016, 25(6): 88-93. DOI:10.15888/j.cnki.csa.005202 |
| [3] |
余修武, 范飞生, 周利兴, 等. 无线传感器网络自适应预测加权数据融合算法. 传感技术学报, 2017, 30(5): 772-776. DOI:10.3969/j.issn.1004-1699.2017.05.023 |
| [4] |
潘泉, 程咏梅, 梁彦, 等. 多源信息融合理论及应用. 北京: 清华大学出版社, 2013.
|
| [5] |
彭冬亮, 文成林, 薛安克. 多传感器多源信息融合理论及应用. 北京: 科学出版社, 2010.
|
| [6] |
李洪伟, 刘兆东, 闵远胜, 等. 多源数据融合方法研究. 核动力工程, 2018, 39(3): 77-80. |
| [7] |
范时平, 何超杰. 基于NARX神经网络的分簇数据融合算法. 计算机工程与设计, 2018, 39(3): 938-942. |
| [8] |
张明阳, 沈明玉. 基于WSN的数据融合在水质监测中的研究. 计算机工程与应用, 2014, 50(23): 234-238, 260. DOI:10.3778/j.issn.1002-8331.1301-0123 |
| [9] |
谭德坤, 付雪峰, 赵嘉, 等. 基于异常数据驱动的WSN簇内数据融合方法. 传感技术学报, 2017, 30(2): 306-312. DOI:10.3969/j.issn.1004-1699.2017.02.024 |
| [10] |
邓振文, 孙启湲, 贾云伟, 等. 可应用于气体泄漏源搜寻的融合算法. 计算机科学, 2016, 43(8): 212-215. DOI:10.11896/j.issn.1002-137X.2016.08.043 |
| [11] |
Jing GL, Du WT, Guo YY. Studies on prediction of separation percent in electrodialysis process via BP neural networks and improved BP algorithms. Desalination, 2012, 291: 78-93. DOI:10.1016/j.desal.2012.02.002 |
| [12] |
章巍. 基于D-S证据理论的数据融合方法设计与实现[硕士学位论文]. 北京: 北京邮电大学, 2018.
|
| [13] |
Xiao FY. A novel evidence theory and fuzzy preference approach-based multi-sensor data fusion technique for fault diagnosis. Sensors, 2017, 17(11): 2504. DOI:10.3390/s17112504 |
| [14] |
Zhu PY, Xiong WL, Qin NN, et al. D-S theory based on an improved PSO for data fusion. Journal of Networks, 2012, 7(2): 370-376. |
| [15] |
高杨, 沈重, 张永辉. 基于多传感器数据融合技术的臭氧监测系统设计. 传感器与微系统, 2014, 33(5): 66-68, 72. DOI:10.3969/j.issn.1000-9787.2014.05.020 |
 2019, Vol. 28
2019, Vol. 28

