2. 北京交通大学 下一代互联网互联设备国家工程实验室, 北京 100044
2. National Engineering Laboratory for NGI Interconnection Devices, Beijing Jiaotong University, Beijing 100044, China
近年来, 基于位置的社交网络服务(Location-Based Social Network, LBSN)得到迅速发展, 如Loopt、Yelp、Foursquare、Whrrl等[1]. 在这些LBSNs中, 用户访问线下的兴趣点(Point-Of-Interest, POI), 如: 餐馆、电影院、博物馆等, 在线上进行“签到”活动, 并分享他们访问兴趣点时丰富的建议与经历[2]. 兴趣点推荐可以减少用户的搜寻时间, 为商家提供精准营销策略. 所以如何利用这些信息, 为目标用户推荐正确的兴趣点集是一个很有前途、很有趣的研究问题. 目前, 有很多学者运用协同过滤、矩阵分解、LDA模型等技术于兴趣点推荐之中, 但是普遍存在以下几个问题:
(1) 数据稀疏问题. 在LBSNs中兴趣点推荐研究遭遇到了严重的数据稀疏问题. 通常情况下, 一个用户访问的兴趣点的数量仅仅是兴趣点总数当中很小的一部分. 例如, Netflix电影推荐的数据密度是1.2%, 而兴趣点推荐研究实验中使用的数据密度通常在0.1%左右[3]. Ye等人[4]提出了融合地理位置、用户偏好和社会影响的统一协同过滤模型, Lian等人[5]提出了加权矩阵分解模型, 均容易受到数据稀疏性的影响. 协同过滤算法利用用户之间的相似性进行有效地推荐, 很容易受到数据稀疏性的影响. 而且该算法只考虑到了签到数据的显式反馈, 不能有效地融合异构数据源[6]. 矩阵分解算法可缓解数据稀疏性的影响, 但是其忽略了用户之间的相似性.
(2) 隐私问题. 很多保护隐私意识比较强的用户, 他们在LBSNs中不会透露家庭住址、公司地址等有效信息. Li等人[7]考虑了用户“家”的地理位置, 认为单考虑地理位置影响则家与兴趣点之间的距离同其访问该兴趣点的概率呈幂律分布. 但在这些信息不完全甚至是没有这些信息的情况下, 如何进行有效的兴趣点推荐是我们要研究的问题之一.
(3) 类别信息. 每个兴趣点都会有其类别信息, 如: 饭店、电影院、博物馆等. 从历史签到记录来看, 每个用户都会偏向于访问类别相同或者相似的兴趣点[7]. 因此, 如何利用兴趣点的类别信息提高兴趣点推荐的准确率是我们研究内容的重点.
本文针对上述的问题, 提出了SoGeoCat(Social-Geography-Category, SoGeoCat)模型, 主要贡献如下:
(1) SoGeoCat模型结合了协同过滤算法和矩阵分解算法的优点, 首先根据用户行为相似性发现目标用户的潜在兴趣点, 然后将潜在兴趣点纳入矩阵分解模型当中, 克服了单纯协同过滤和矩阵分解算法的不足, 即考虑了用户相似度又很大程度上缓解了数据稀疏性的问题.
(2) 本文利用贝叶斯规则, 根据目标用户的历史签到轨迹来判断拟推荐兴趣点在地理位置因素上对目标用户的影响.
(3) 本文将兴趣点的类别标签纳入矩阵分解模型中, 提高SoGeoCat模型的推荐效率.
1 相关工作协同过滤和矩阵分解是兴趣点推荐研究中主流的两种算法.
(1) 基于协同过滤算法的推荐. 协同过滤的主要思想是: 分析用户之间的关系和项目之间的相互依赖关系, 以识别新的用户—项目关联[8–10].
Ye等人[4]提出了融合地理位置、用户偏好和社会影响的统一协同过滤方法. 采用幂律概率模型捕捉兴趣点之间的地理位置影响, 通过朴素贝叶斯方法实现基于地理影响的兴趣点协同推荐. Yuan等人[11]在统一的协同过滤框架上纳入了时间信息的影响, 利用时间感知进行兴趣点推荐. 但该算法很容易受到数据稀疏性的影响, 也不能很好地实现对隐式反馈数据集的挖掘.
(2) 基于矩阵分解算法的推荐. 矩阵分解法的核心是训练出用户和兴趣点的特征向量, 并以此来预测用户对于某一特定兴趣点的偏好. 其不仅可以缓解数据稀疏性的影响还可以融合异构数据源, 考虑隐式反馈数据集[5, 12–14].
Lian等人[5]将地理位置影响纳入加权矩阵分解框架当中, 根据签到记录的空间聚集现象, 提出了GeoMF模型, 模拟用户活动区域与地理位置之间的影响关系. 高榕等人[14]在经典的矩阵分解模型的基础上, 融合异构数据, 提出了GeoSoRev模型, 采用基于矩阵分解的主题模型来发现评论中的隐藏“主题”. 矩阵分解算法虽然缓解了数据的稀疏性, 也融合不同的异构数据, 但它没有考虑到用户之间的相似性.
(3) 混合算法推荐. 为了克服两种算法的不足之处, 有一些学者提出了混合算法. Li等人[7]提出了“两步走”的框架. 第一步设计基于线性聚集和基于随机游走两种方法, 为每个用户学习一组他们可能感兴趣的潜在兴趣点. 在第二步骤中, 用基于平方误差的损失函数和基于排名误差的损失函数来模拟这三种签到.
文献[5]中认为用户的签到概率和从家到相应位置的距离遵循幂律分布. 一方面, 家的位置信息较难获得, 很多用户隐私保护意识越来越强, 不愿意透露家庭位置信息; 另一方面, 用户签到过的兴趣点可能会聚集在某两个距离比较远的区域, 如家和公司附近. 因此, 本文针对上述问题, 在文献[5]的基础上继续研究, 提出了SoGeoCat (Social-Geography-Category)模型, 用朴素贝叶斯方法计算地理位置因素对于用户决策的影响, 保护用户家庭位置信息, 并将签到信息、朋友信息、地理位置信息和类别信息纳入混合模型中, 即考虑了用户相似性又缓解了数据稀疏问题, 提高了模型的推荐效果.
2 用户潜在兴趣点数据模型 2.1 问题描述本文主要研究的问题与传统的基于协同过滤的推荐模型或基于矩阵分解的推荐模型不同, 而是采用了“两步走”的框架模型SoGeoCat: 首先, 建立用户潜在兴趣点数据模型, 利用用户的签到信息、朋友信息、地理位置信息对用户的签到信息进行有效地扩充; 然后, 建立一个融合类别标签的矩阵分解模型, 训练出用户特征矩阵和兴趣点特征矩阵; 最后考虑用户特征、兴趣点特征的影响, 估算出目标用户对于某一特定的兴趣点的访问概率, 进而推荐有效的兴趣点集.
假设ui为目标用户,lj为拟推荐兴趣点. U为用户集, 即U={u1,u2,…,un}, L为兴趣点集, 即L={l1,l2,…,lm}. 运用SoGeoCat模型计算出ui访问每一个未访问过的POI的概率, 选取Top S作为ui的拟推荐兴趣点集.
2.2 基于签到行为相似度建模用户在LBSNs中有大量的签到信息, 签到信息包括用户ID, 兴趣点ID和访问次数. 访问次数越多, 则说明用户对该兴趣点的偏好越强. 用户i与用户u已签到过的共同的兴趣点越多, 则他们的签到行为越相似, 即签到行为相似度Sim(ui, uu)越高, 本文采用余弦相似度来度量两用户之间的签到行为相似度, 建模如下:
| $S{{im}}\left( {{{{u}}_{{i}}},{{{u}}_{{u}}}} \right) = {\left( {\sum\limits_{{{z}} \in M_i^o} {r_{i,z}^2} \sum\limits_{z \in M_u^o} {r_{u,z}^2} } \right)^{ - \frac{1}{2}}}\sum\limits_{z \in M_i^o \cap M_u^o} {r_{i,z}^{}} r_{u,z}^{}$ | (1) |
其中,
注意: 这里的uu曾经在兴趣点lj处有签到行为.
2.3 基于朋友相似度建模用户在LBSNs上有一些相互关注的好友, 这些好友关系也反映了该用户在现实生活中的朋友圈. 现实中, 你朋友的推荐会激发你对某些兴趣点的兴趣, 在LBSNs中亦是如此. 所以, uf(ui的朋友)的签到记录很有可能是ui想要访问的潜在兴趣点. 但是ui有很多好友, 不一定每一个好友签到过的兴趣点, ui都会感兴趣. 对此, 提出了朋友相似度Sim(ui, uf), 朋友相似度越高, 其历史签到记录越有参考价值, 建模如下:
| $S{{im}}\left( {{{{u}}_{{i}}},{{{u}}_{{f}}}} \right) = {\left( {\sum\limits_{{{z}} \in M_i^o} {r_{i,z}^2} \sum\limits_{z \in M_f^o} {r_{f,z}^2} } \right)^{ - \frac{1}{2}}}\sum\limits_{z \in M_i^o \cap M_f^o} {r_{i,z}^{}} r_{f,z}^{}$ | (2) |
其中,
注意: 这里的uf曾经在兴趣点lj处有签到行为.
2.4 基于地理位置相似度建模人们往往喜欢访问地理位置离自己近的兴趣点, 单考虑地理位置影响因素, 用户访问兴趣点的概率同其距离遵循幂率分布, 模型[5]如下:
| $P{{r}}\left( {{d}} \right) = a \cdot {d^b}$ | (3) |
其中,d表示用户同兴趣点之间的距离, a和b均为幂律分布的参数.
但是, 在本文中只有用户历史签到记录信息, 没有用户的实时地理位置信息, 所以, 不能算出用户与某一兴趣点之间的准确距离. 为了解决此问题, 且又能保护用户的家庭住址或公司地址等常驻地址信息, 本文采用了基于朴素贝叶斯规则的模型,计算地理位置相似度
| $\begin{aligned}P\left( {{l_j}\left| {{L_{{u_i}}}} \right.} \right) & = \frac{{P\left( {{l_j} \cup {L_{{u_i}}}} \right)}}{{P\left( {{L_{{u_i}}}} \right)}} = \frac{{P\left( {{L_{{u_i}}}} \right) \times \displaystyle\prod\limits_{{l_k} \in {L_{{u_i}}}} {P\left( {{l_k}\left| {{l_j}} \right.} \right)} }}{{P\left( {{L_{{u_i}}}} \right)}} \\&=\prod\limits_{{l_k} \in {L_{{u_i}}}} {P\left( {{l_k}\left| {{l_j}} \right.} \right)} \end{aligned}$ | (4) |
注意: 这里假定
综合考虑上述三个因素的影响, 对签到行为相似度、朋友相似度和地理位置相似度进行线性聚合. 但是, 它们是通过不同的方法来衡量的, 具有不同的价值范围. 因此, 我们采用最小-最大归一化进行处理, 然后再进行聚集.
同时, 签到次数也能侧面地反映用户的偏好. 根据公式(8)计算出ui对于拟推荐兴趣点lj的分数, 选取分数高的前S个兴趣点作为ui的潜在兴趣点.
| $Sim'\left( {{u_i},{u_u}} \right) = \frac{{Sim\left( {{u_i},{u_u}} \right){\rm{ - min}}\left( {Sim\left( {{u_i},{u_u}} \right)} \right)}}{{{\rm{max}}\left( {Sim\left( {{u_i},{u_u}} \right)} \right){\rm{ - min}}\left( {Sim\left( {{u_i},{u_u}} \right)} \right)}}$ | (5) |
| $P'\left( {{l_{{j}}}|{L_{{u_i}}}} \right) = \frac{{P\left( {{l_{{j}}}|{L_{{u_i}}}} \right){\rm{ - }}\min\left( {P\left( {{l_{{j}}}|{L_{{u_i}}}} \right)} \right)}}{{\max\left( {P\left( {{l_{{j}}}|{L_{{u_i}}}} \right)} \right){\rm{ - }}\min\left( {P\left( {{l_{{j}}}|{L_{{u_i}}}} \right)} \right)}}$ | (6) |
| $S{{im}}\left( {{{\rm{u}}_{\rm{i}}},{l_j}} \right) = \zeta \max \left( {Sim'\left( {{u_i},{u_u}} \right)} \right) + \left( {1 - \zeta } \right)P'\left( {{l_{\rm{j}}}|{L_{{u_i}}}} \right)$ | (7) |
| ${\rm{score}} = S{{im}}\left( {{{{u}}_{{i}}},{l_j}} \right) \times {{ratin}}{{{g}}_{{{u}},j}}$ | (8) |
其中, U表示与ui访问过相同兴趣点的用户及ui的朋友的集合且
用户ui对于兴趣点lj的偏好程度受用户潜在特征和兴趣点潜在特征影响. 令用户特征矩阵为U, 兴趣点特征矩阵为V, 偏好矩阵为P, 则:
| $P \approx \hat P = {U^{\rm T}}V$ | (9) |
用
| ${P_{{{ij}}}} = \left\{ \begin{array}{l}{\rm{1}}\;\;\;\;\;\;\;{\rm{if}}\;{{j}} \in {{M}}_{{i}}^{{o}}\\\alpha \;\;\;\;\;\;{\rm{if}}\;{{j}} \in {{M}}_{{i}}^{{p}}\\{{0}}\;\;\;\;\;\;{\rm{otherwise}}\end{array} \right.\;\;\;{\rm{where}}\;\;\alpha \in \left[ {{\rm{0}},{\rm{1}}} \right]$ | (10) |
其中,
在LBSNs的兴趣点推荐中, 其类别信息发挥着重要的作用. 从历史签到记录来看, 每个用户都会偏向于访问类别相同或相似的兴趣点, 如: ui之前经常访问饭店, 但几乎没去过电影院, 此时如果给他推荐电影院, 则其访问的可能性就会大大降低. 设
| ${\hat P_{{{ij}}}} = \left( {{{{q}}_{{{i}}{{{c}}_{{j}}}}} + \varepsilon } \right)u_i^{\rm T}{v_j}$ | (11) |
其中,
损失函数为:
| $\mathop {\min }\limits_{U,V,Q} \left\| {W \odot \left( {P - \hat P} \right)} \right\|_2^2 + \frac{{{\lambda _u}}}{2}\left\| U \right\|_2^2 + \frac{{{\lambda _v}}}{2}\left\| V \right\|_2^2 + \frac{{{\lambda _q}}}{2}\left\| Q \right\|_2^2$ | (12) |
其中,
| ${w_{ij}} = \left\{ \begin{array}{l}1 + {\sqrt {{\rm{1}} + \gamma \times r} _{ij}}\;\;\;\;{\rm{if }}\;\;j \in {{M}}_{{i}}^{{o}}\\1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise }}\end{array} \right.$ | (13) |
其中,
本文采用变更最小二乘(ALS)优化损失函数, 训练出特征矩阵U,V和类别特征矩阵Q. U,V,Q的更新公式如下:
| ${{{u}}_{{i}}} = {\left( {{\lambda _{{u}}}{I_{{k}}} + {{\sum\limits_j {{w_{ij}}\left( {{q_{i{c_j}}} + \varepsilon } \right)} }^2}{v_j}v_j^{\rm T}} \right)^{ - 1}}\sum\limits_j {{w_{ij}}\left( {{q_{i{c_j}}} + \varepsilon } \right)} {p_{ij}}v_j^{}$ | (14) |
| ${{{v}}_{{j}}} = {\left( {{\lambda _{{v}}}{I_{{k}}} + {{\sum\limits_i {{w_{ij}}\left( {{q_{i{c_j}}} + \varepsilon } \right)} }^2}{u_i}u_i^{\rm T}} \right)^{ - 1}}\sum\limits_i {{w_{ij}}\left( {{q_{i{c_j}}} + \varepsilon } \right)} {p_{ij}}u_i^{}$ | (15) |
| ${{{q}}_{{{ic}}}} = \frac{{\left( {\displaystyle\sum\limits_{j \in {N_c}} {{w_{ij}}\left( {{p_{ij}} - \varepsilon } \right){{\left( {u_i^{\rm T}{v_j}} \right)}^2}} } \right)}}{{\left( {{\lambda _q} + \displaystyle\sum\limits_{j \in {N_c}} {{w_{ij}}{{\left( {u_i^{\rm T}{v_j}} \right)}^2}} } \right)}}$ | (16) |
其中, Ik为k维单位矩阵, Nc为类别为c的兴趣点的集合.
4 实验 4.1 实验数据集本实验的数据来自Foursquare真实数据集[13], 采集的是2009年12月至2013年6月期间在加利福尼亚的签到数据, 包括用户ID、朋友信息、兴趣点ID、兴趣点经纬度及其类别信息. 数据集中一共含有2551名用户, 13 474个兴趣点及124 933条签到记录. 用户-兴趣点矩阵密度为0.002 91. 由于LBSNs中存在严重的数据稀疏性, 所以LBSNs背景下的推荐模型准确率和召回率普遍较低. 数据集的相关内容详见表1.
为了验证SoGeoCat模型的准确性, 对Foursquare数据集做了如下的处理.
| 表 1 实验数据集 |
1) 剔除访问少于10个兴趣点的用户.
2) 剔除少于10个用户访问的兴趣点.
3) 采用数据集中的80%的数据作为训练集, 剩余的20%作为测试集.
4.2 评价指标本文采用准确率(Precision)和召回率(Recall)来评估推荐算法的性能, 计算公式如下:
| $P{\rm{@}}k = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{T\left( {{u_i}} \right) \cap H\left( {{u_i}} \right)}}{k}} $ | (20) |
| $R{\rm{@}}k = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{T\left( {{u_i}} \right) \cap H\left( {{u_i}} \right)}}{{T\left( {{u_i}} \right)}}} $ | (21) |
其中,
实验中, 我们将k设置为: 5, 8, 10, 12, 15, 20.
4.3 推荐模型对比为了评估SoGeoCat模型的性能, 本文选取三个经典模型同本模型进行对比:
IRenMF[15]采用了融合地理位置信息的矩阵分解模型, 根据地理特征将领域分为实例级别领域和区域级别领域这两个层次, 利用领域的特征进行个性化推荐;
USG[4]采用了统一的协同过滤框架, 综合考虑了用户偏好、朋友信息和地理位置信息对兴趣点推荐的影响;
ASMF-LA[13]采用了“两步走”框架, 融合用户偏好、朋友信息、地理位置信息和类别信息对兴趣点推荐的影响.
参考文献[13], 实验的相关参数设置如下:
特征矩阵维度l设置为12;
为了评估SoGeoCat模型的性能, 本节从推荐模型(USG、IRenMF、ASMF-LA、SoGeoCat)之间比较、SoGeoCat模型中各要素影响和用户潜在兴趣点数据模型影响这三个方面进行分析, 具体内容如下.
4.4.1 推荐模型的比较与分析在k=5, 8, 10, 12, 15, 20的条件下准确率和召回率分别用P@k、R@k表示, 各模型的准确率和召回率见表2.
| 表 2 各模型在Foursquare数据集中的性能 |
|
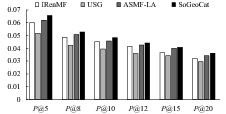
图 1 基于Foursquare数据集各模型的准确率对比 |
|
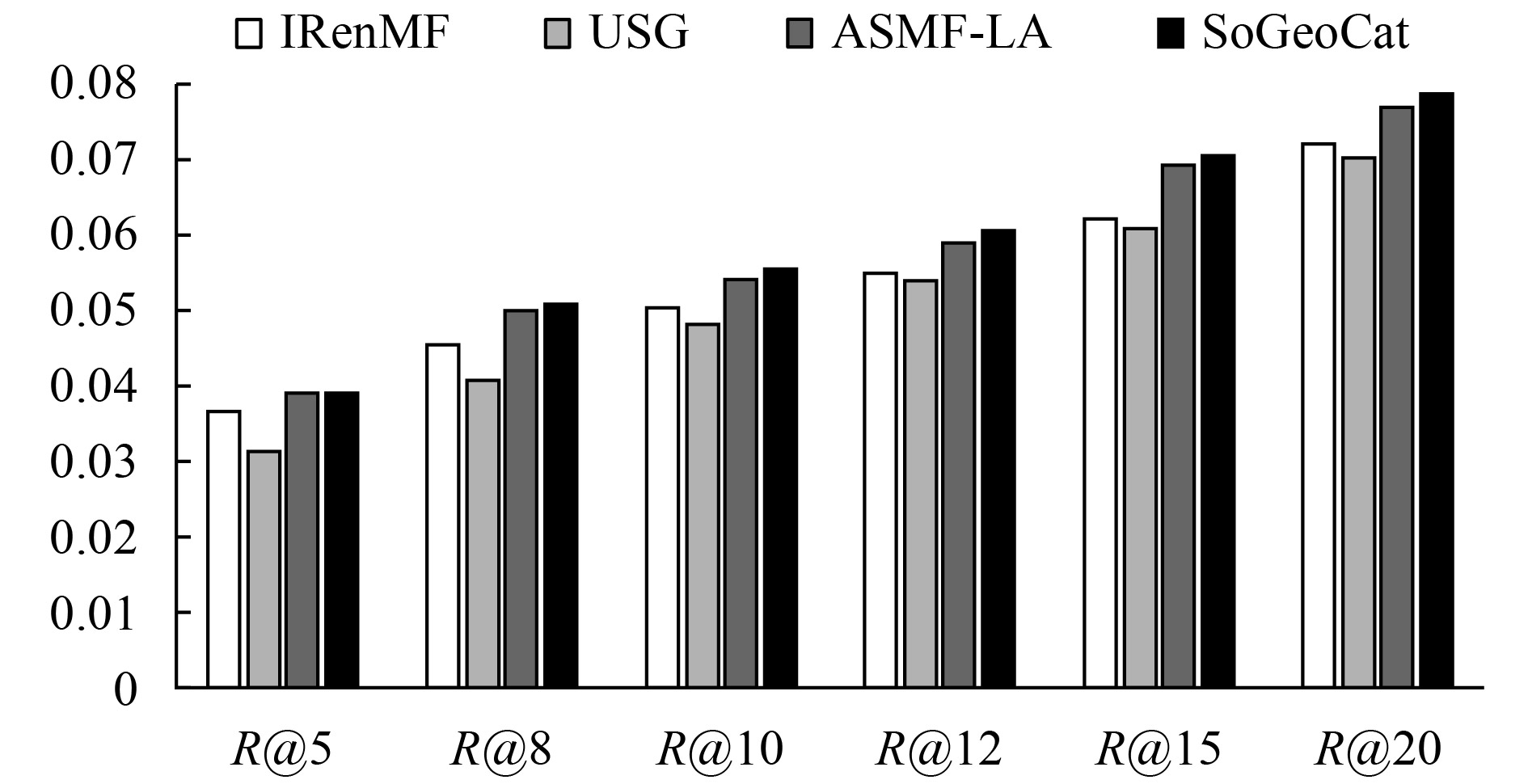
图 2 基于Foursquare数据集各模型的召回率对比 |
从表2中可以看出:
(1) IRenMF采用了加权矩阵分解模型, 对于实例级别领域和区域级别领域分别采用兴趣点相似性和用户相似性进行个性化推荐, 但由于没考虑朋友信息和类别信息, 因此相对于ASMF-LA和SoGeoCat而言表现出了更差的推荐效果, 如表三所示, IRenMF表现出了第3好的推荐效果;
(2) USG是采用了融合用户偏好、朋友信息和地理位置信息的统一协同过滤模型, 但由于其没有考虑类别信息, 且各要素的影响只是进行简单的线性加权组合, 忽略了要素之间的相互作用, 再者, 协同过滤算法很容易受到数据稀疏性的影响. 所以, USG模型表现出最差的推荐效果;
(3) ASMF-LA采用了“两步走”框架, 考虑了直接朋友、邻居朋友、位置朋友和类别信息对兴趣点推荐的影响, 表现出了不错的推荐效果. 但是在获取邻居朋友和计算地理位置因素对兴趣点推荐的影响时, 都需要用到用户“家”的信息. 实际上, 越来越多的用户不愿意公开自己“家”的位置等隐私信息, 而且, 并非用户只愿意访问离家近的兴趣点, 如: 白领小A, 他家和公司相离10公里, 他经常访问的兴趣点就容易集中在以家和公司为圆心的两个领域当中. 所以, ASMF-LA表现出了第2好的推荐效果;
(4) SoGeoCat同样采用了“两步走”框架, 既考虑到了用户之间的相似性, 又缓解了数据稀疏性, 融合了签到信息、朋友信息、地理位置信息和类别信息对兴趣点推荐的影响. 而且, 本模型中, 改进了地理位置对兴趣点推荐的影响, 根据用户的历史签到足迹来估计地理位置因素对目标用户的影响, 保护了用户的隐私信息, 表现出了最好的推荐效果.
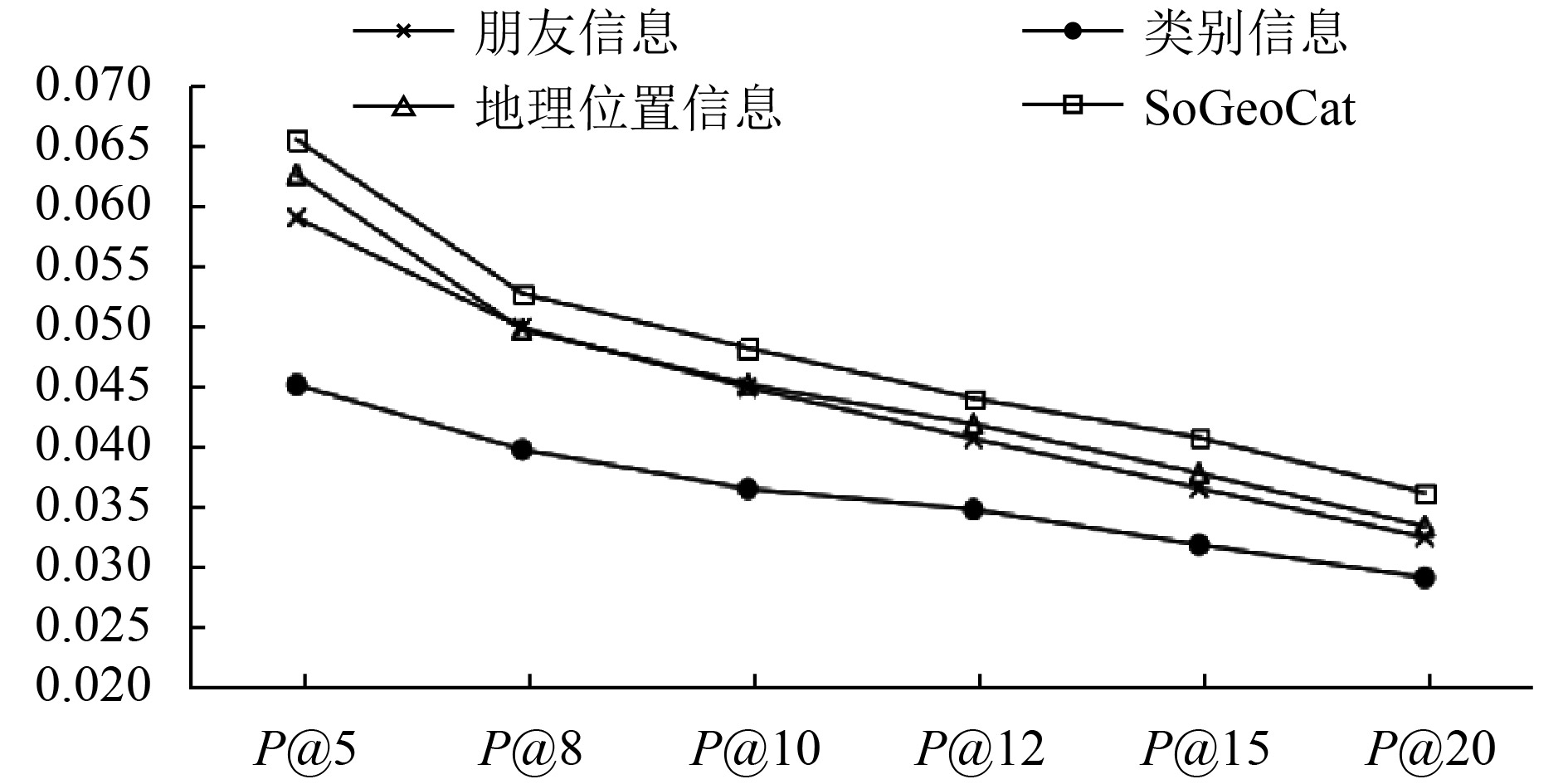
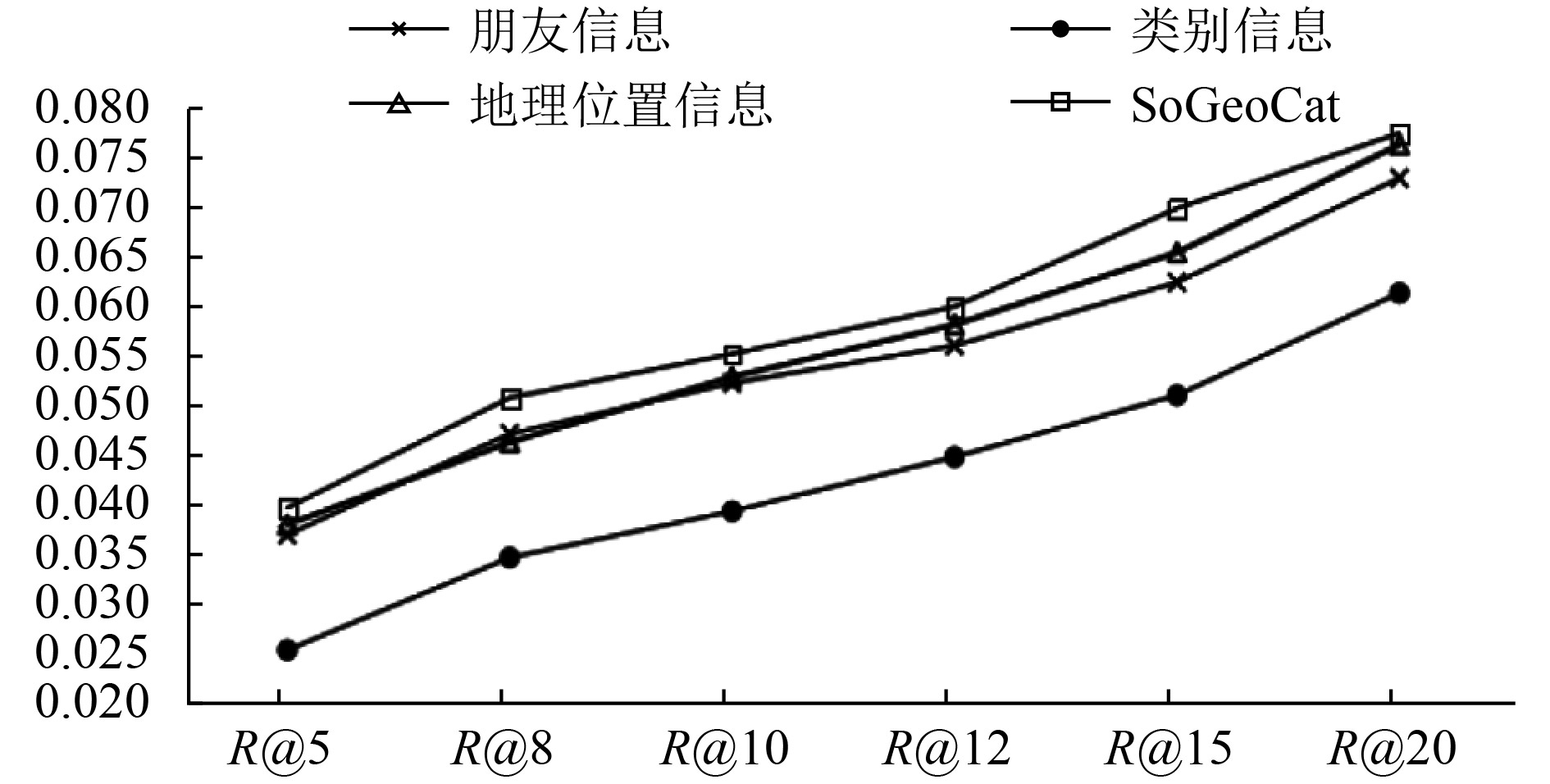
4.4.2 要素影响分析从图3、图4中我们可以看出: (1)三个要素对于兴趣点推荐都发挥着重要作用, 且融合三个要素时推荐效果最好; (2)朋友信息、地理位置信息对兴趣点推荐的影响大于类别信息对于推荐的影响. 分析其原因, 主要在于用户在选择兴趣点时受到了多个方面的影响, 如朋友的介绍、距离的远近和自己的爱好等等, 所以我们不能片面地根据某一影响因素进行建模. 在SoGeoCat模型的第二步中运用了矩阵分解算法, 在矩阵分解算法中训练出的用户特征向量和矩阵特征向量中也有考虑到社会关系、地理位置等因素的影响, 但是在特征矩阵中没有具体地说明.
|
图 3 基于Foursquare数据集各要素间的准确率对比 |
|
图 4 基于Foursquare数据集各要素间的召回率对比 |
4.4.3 用户潜在兴趣点数据模型影响分析
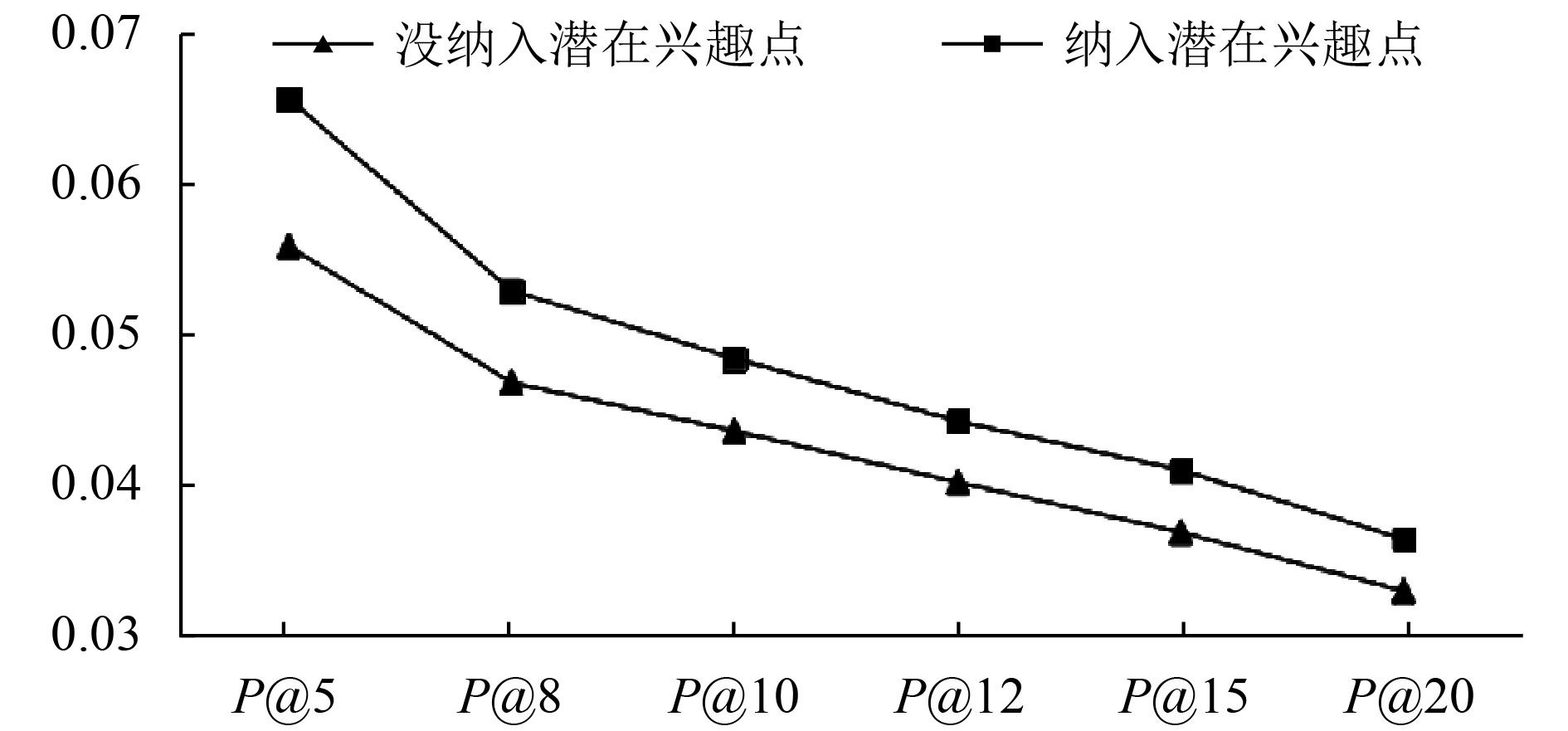
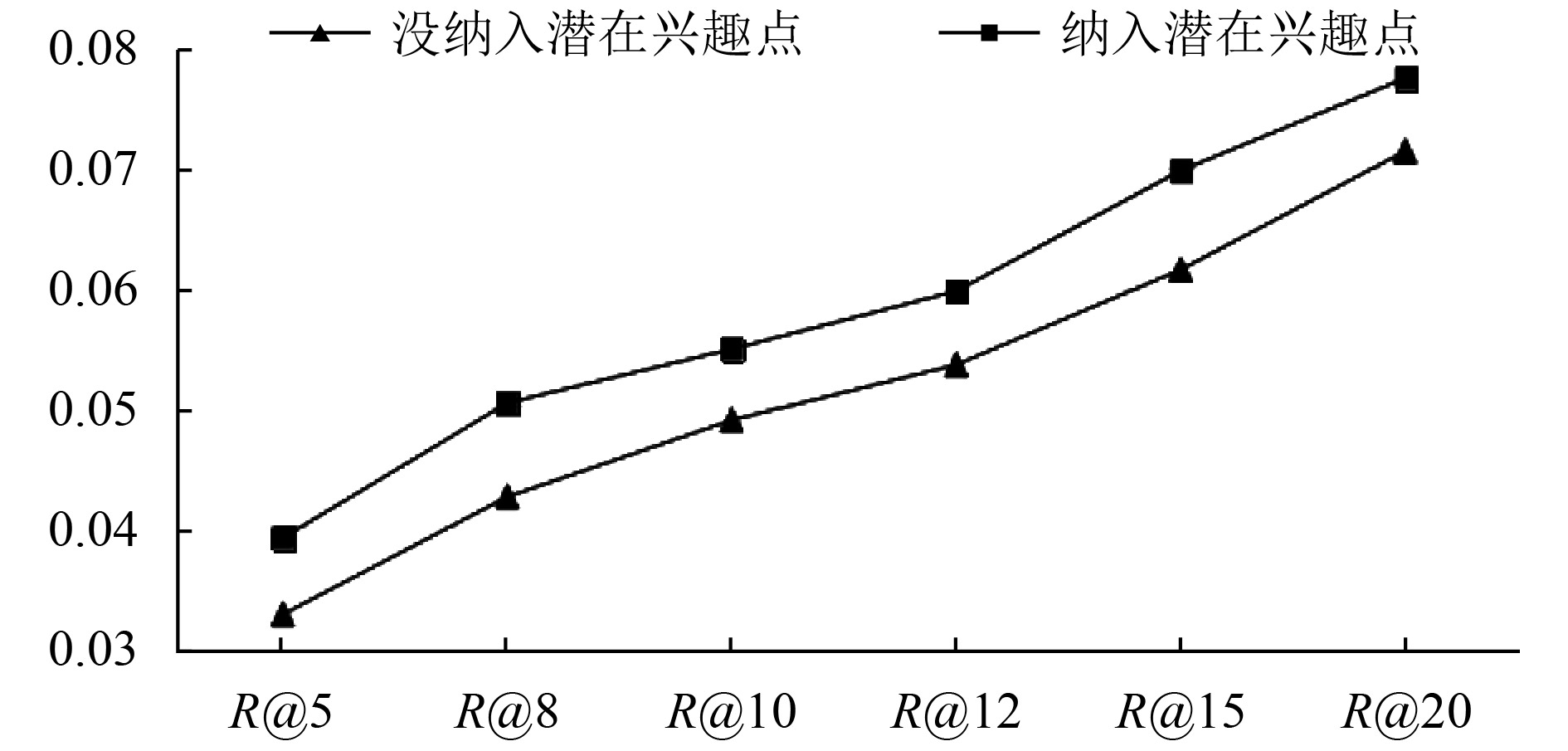
在这个部分中, 我们比较纳入用户潜在兴趣点数据模型的推荐模型和未纳入用户潜在兴趣点数据模型的推荐模型的推荐效果, 图5、图6结果表明, 纳入用户潜在兴趣点数据模型的推荐效果优于未纳入用户潜在兴趣点数据模型的推荐效果. 分析其原因, 主要有两点: (1)虽然矩阵分解算法中已经将朋友信息、类别信息和地理位置信息考虑在特征矩阵之中, 但是不能确切地说明. 我们通过用户潜在兴趣点数据模型, 单独考虑了朋友信息和地理位置信息的影响, 利于发挥其对推荐效果的影响; (2)用户潜在兴趣点数据模型不仅考虑了这三个要素, 它还为偏好矩阵填充了大量的潜在兴趣点的签到信息, 缓解了数据稀疏性.
还有一个有趣的发现, 表2中只考虑类别信息的模型的推荐效果低于未纳入用户潜在兴趣点数据模型的的推荐模型的推荐效果. 因为前者在计算用户潜在兴趣点数据模型时, 没有考虑朋友信息和地理位置信息, 使得计算出来的潜在兴趣点与实际用户偏好有较大的出入, 于是将其带入矩阵分解算法中的时候产生了噪声, 影响推荐效果.
5 结论与展望SoGeoCat模型采用了混合算法, 融合了两种算法的优点, 既考虑了用户之间的相似性又缓解了数据稀疏问题. SoGeoCat模型还融合了类别标签, 保护了用户的常驻位置信息. 通过对真实的Foursquare数据集进行实验, 实验结果表明, SoGeoCat模型相对于其他三个对比模型而言在Precision和Recall上都表现出较好的推荐效果.
|
图 5 基于Foursquare数据集是否纳入潜在兴趣点模型的准确率对比 |
|
图 6 基于Foursquare数据集是否纳入潜在兴趣点模型的召回率对比 |
未来, 希望在此模型的基础上, 纳入“时间信息”和“评论信息”等上下文信息, 进一步地提高推荐算法的精确度和召回率.
| [1] |
曹玖新, 董羿, 杨鹏伟, 等. LBSN中基于元路径的兴趣点推荐. 计算机学报, 2016, 39(4): 675-684. |
| [2] |
余永红. 融合多源信息的推荐算法研究[博士学位论文]. 南京: 南京大学, 2017.
|
| [3] |
Bell RM, Koren Y. Lessons from the Netflix prize challenge. ACM SIGKDD Explorations, 2007, 9(2): 75-79. DOI:10.1145/1345448 |
| [4] |
Ye M, Yin PF, Lee WC, et al. Exploiting geographical influence for collaborative point-of-interest recommendation. Proceedings of the 34th International ACM SIGIR Conference on Research and development in Information Retrieval. Beijing, China. 2011. 325–334.
|
| [5] |
Lian DF, Zhao C, Xie X, et al. GeoMF: Joint geographical modeling and matrix factorization for point-of-interest recommendation. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA. 2014. 831–840.
|
| [6] |
Liu YD, Pham TAN, Cong G, et al. An experimental evaluation of point-of-interest recommendation in location-based social networks. Proceedings of the VLDB Endowment, 2017, 10(10): 1010-1021. DOI:10.14778/3115404 |
| [7] |
Li HY, Ge Y, Hong RC, et al. Point-of-interest recommendations: Learning potential check-ins from friends. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, CA, USA. 2016. 975–984.
|
| [8] |
杨志文, 刘波. 基于Hadoop平台协同过滤推荐算法. 计算机系统应用, 2013, 22(7): 108-112. DOI:10.3969/j.issn.1003-3254.2013.07.024 |
| [9] |
冯晓敏. 基于项目综合相似度和因子分析的协同过滤算法研究[硕士学位论文]. 青岛: 中国石油大学(华东), 2013.
|
| [10] |
范波, 程久军. 用户间多相似度协同过滤推荐算法. 计算机科学, 2012, 39(1): 23-26. DOI:10.3969/j.issn.1002-137X.2012.01.005 |
| [11] |
Yuan Q, Cong G, Ma ZY, et al. Time-aware point-of-interest recommendation. Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval. Dublin, Ireland. 2013. 363–372.
|
| [12] |
Zheng N, Jin XM, Li LH. Cross-region collaborative filtering for new point-of-interest recommendation. Proceedings of the 22nd International Conference on World Wide Web. Rio de Janeiro, Brazil. 2013. 45–46.
|
| [13] |
Li XT, Cong G, Li XL, et al. Rank-GeoFM: A ranking based geographical factorization method for point of interest recommendation. Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval. Santiago, Chile. 2015. 433–442.
|
| [14] |
高榕, 李晶, 杜博, 等. 一种融合情景和评论信息的位置社交网络兴趣点推荐模型. 计算机研究与发展, 2016, 53(4): 752-763. |
| [15] |
Liu Y, Wei W, Sun AX, et al. Exploiting geographical neighborhood characteristics for location recommendation. Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management. Shanghai, China. 2014. 739–748.
|
 2019, Vol. 28
2019, Vol. 28


