作为雾霾的主要元凶之一, PM2.5对人类生活、身心健康、经济发展等都造成了严重影响[1,2]. 如何高效、准确地预测PM2.5值, 进而制定科学合理的雾霾防控方案具有重要意义.
目前, 常用的PM2.5预测方法包括回归模型[3–5]、人工神经网络[6–8]、支持向量机[9,10]等. 其中, 支持向量机(Support Vector Machine, SVM)以其强大的学习泛化能力, 结构风险小的特点, 在小样本、非线性预测领域取得了良好的应用效果. 在实际应用中, SVM参数选择直接影响预测性能, 找到一个合适的算法对SVM参数寻优至关重要. 常用SVM参数优化方法包括: 遗传算法 (Genetic Algorithm, GA)、粒子群算法(Particle Swarm Optimization, PSO)、萤火虫算法(Firefly algorithm, FA)等. 如朱霄珣等[11]使用GA优化SVM参数, 建立风速预测模型. 戴李杰等[12]将GA的变异因子引入到PSO中对SVM参数寻优建立未来24小时PM2.5滚动预报模型. 杨孟英[13]使用FA优化SVM参数, 进行中文文本分类. 相比于GA和PSO, FA结构简单、调节参数少, 易于计算, 能更好地平衡全局和局部性能[14–16], 但标准FA也存在缺陷, 如迭代后期收敛速度慢, 固定步长造成振荡现象等[17–19]. 为此, 本文对标准FA进行改进, 利用改进FA对SVM参数寻优, 构建IFA-SVM的PM2.5预测模型, 用此模型预测太原市未来一天和三天的PM2.5含量, 分析该模型用于PM2.5浓度预测的可行性和高效性.
1 PM2.5预测原理PM2.5预测是依据气象条件、污染源等因素和历史数据建立数学模型来预测未来PM2.5值, 表示为如下非线性关系:
| $y = f\left( {{x_1}, {x_2}, \cdots, {x_n}} \right)$ | (1) |
其中,
由于PM2.5是气象条件、污染源、地理空间等多种因素共同作用的结果[20], 呈现高度非线性, 本文使用SVM来预测PM2.5值.
2 算法理论基础 2.1 SVM基本原理SVM基本思想是针对PM2.5非线性样本, 引入径向基(Radial Basis Function, RBF)核函数, 将样本映射到高维空间, 在高维空间求解超平面, 使得两类样本的间隔最大[21], 即求解如下约束优化问题:
| $\mathop {\min }\limits_{w, b, \xi } \frac{1}{2}{w^{\rm T}}w + C\sum\limits_{i = 1}^i {{\varepsilon _i}} $ | (2) |
其中,
| $K({x_i}, {x_j}) = \exp ( - \gamma {\left| {{x_i} - {x_j}} \right|^2})$ | (3) |
因此影响SVM性能的主要参数即为C、
FA受自然界萤火虫生物特性启发[22], 其对SVM参数优化思想为:
将所有SVM可选参数模拟为萤火虫个体, 将优化过程看作对最优个体的寻找, 即通过个体的吸引和位置移动实现目标参数寻优, 在迭代过程中用好的可行解淘汰较差可行解, 直到得到最优解, 即亮度最高的萤火虫的位置即为最优参数.
算法涉及两个因素, 萤火虫的发光亮度
| $I = {I_0} \times {e^{ - \gamma {r_{ij}}}}$ | (4) |
| $\beta = {\beta _0} \times {e^{ - \gamma {r_{ij}}}}^{^2}$ | (5) |
其中,
寻优过程中萤火虫i被吸引向萤火虫j移动的位置更新公式为:
| ${x_i} = {x_i} + \beta \times ({x_j} - {x_i}) + \alpha \times \left({{rand}} - \frac{1}{2}\right)$ | (6) |
其中,
FA主要步骤包括:
(1)根据目标函数计算萤火虫的亮度;
(2)亮度较暗的萤火虫按公式(6)向较亮的萤火虫移动;
(3)对萤火虫按亮度值从大到小排序, 找到最亮的萤火虫;
(4)重复迭代, 直到达到最大迭代次数.
2.3 基于邻域搜索策略的改进FA标准FA迭代中亮度较暗的萤火虫按公式(6)向较亮的萤火虫移动, 当迭代后期亮度相同时, 萤火虫将随机运动, 此时收敛速度下降且很难找到最优解. 同时若萤火虫个体搜索半径内没有更亮个体, 萤火虫也将随机运动, 此时最优亮度为搜索半径内局部最优而非全局最优, 算法搜索能力下降, 精度较差. 根据文献[19], 设计两种邻域搜索策略为参数寻优提供更多更精确的候选解, 帮助萤火虫跳出局部最优并加速收敛, 具体邻域搜索策略为:
| ${x_i}^1 = {\lambda _1} \times {x_i} + {\lambda _2} \times pbest + {\lambda _3} \times ({x_{i1}} - {x_{i2}})$ | (7) |
其中,
| ${x_i}^2 = {\lambda _4} \times {x_i} + {\lambda _5} \times gbest + {\lambda _6} \times ({x_{i3}} - {x_{i4}})$ | (8) |
其中,
如果迭代过程中, 第t次迭代萤火虫亮度值与t-1次亮度值相等, 执行上述两种策略, 找到其它两个候选解
标准FA中, 步长因子
| $\alpha = 0.4/(1 + \exp (0.015 \times (t - maxG)/3))$ | (9) |
其中,
IFA-SVM PM2.5预测过程如下:
(1)收集太原市PM2.5浓度实验数据, 划分训练集和测试集, 并归一化预处理;
(2) IFA-SVM参数迭代寻优
1)初始化算法各基本参数, 随机分布萤火虫;
2)计算萤火虫的目标函数值, 以SVM对训练集的PM2.5预测性能作为目标函数值;
3)对萤火虫的目标函数值进行亮度排序, 找到当前最优的目标函数值及其对应萤火虫, 并根据公式(6)更新萤火虫;
4)如果迭代过程中, 第t次迭代目标函数值与t–1迭代目标函数值相等, 执行2.3节中两种邻域搜索策略;
5)若达到最大迭代次数, 或满足停止迭代的条件, 则转至步骤6), 否则转至步骤2)继续迭代;
6)输出最大目标函数值及其对应的萤火虫, 即得到最优参数.
(3)使用最优参数预测测试集PM2.5值, 并将预测结果反归一化, 得到实际PM2.5预测值, 输出结果.
具体流程如图1所示.
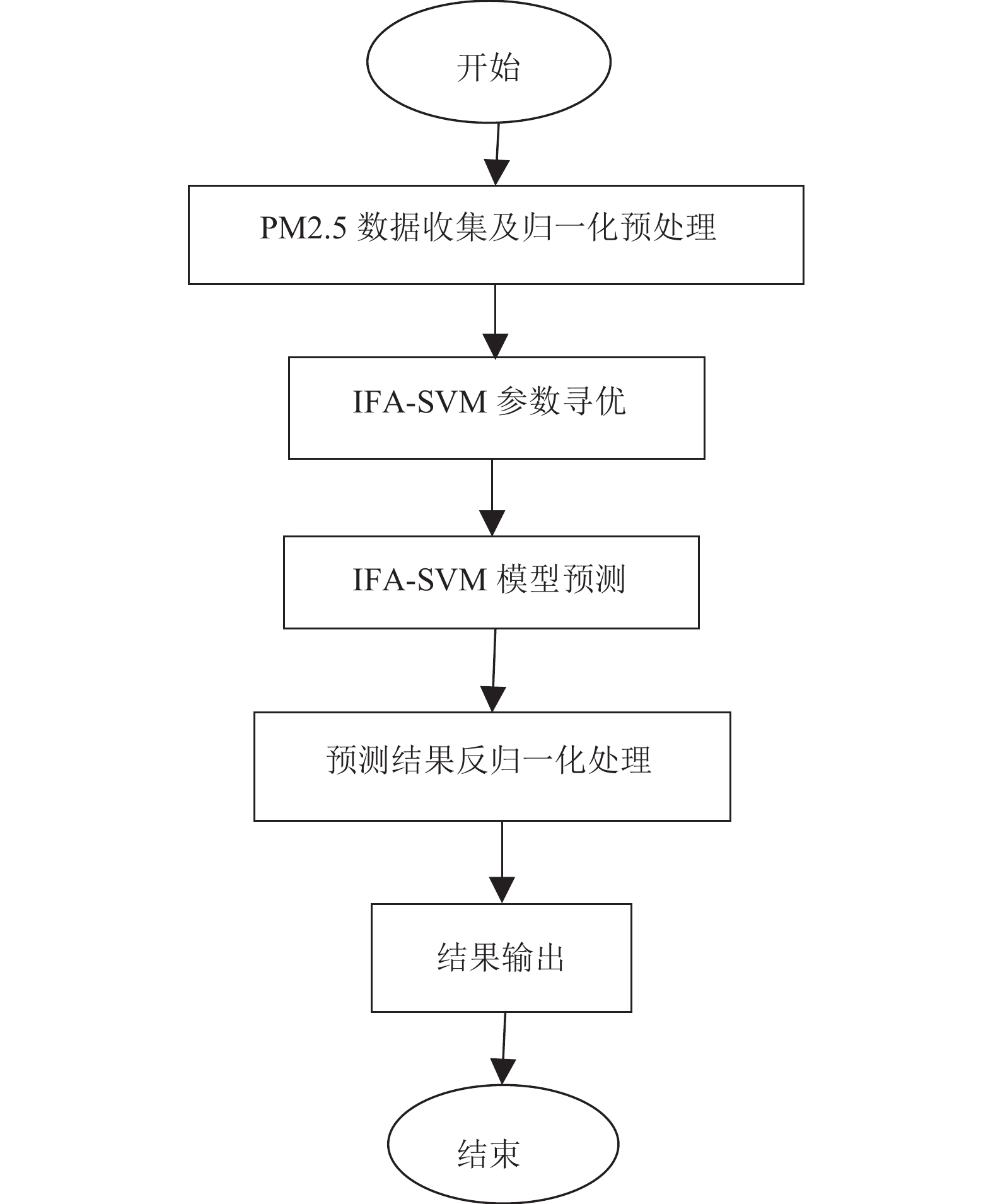
|
图 1 IFA-SVM PM2.5预测流程 |
3.2 数据收集及预处理
统计发现, 太原市秋冬季节出现雾霾频率更高, 综合考虑气象条件和污染源, 收集太原市2015.10~2016.3、2016.10~2017.3和2017.11的湿度、露点、气压、风速、O3、CO、NO2、PM10共8项PM2.5影响因子进行建模. 具体如表1所示, 其中, 2015.10~2016.3、2016.10~2017.3作为训练样本, 2017.11作为测试样本.
为了消除各影响因子量纲不同对预测速度和精度的影响, 建模之前进行归一化预处理, 归一化公式为:
| $x_i' = \left( {{x_i} - {x_{\min }}} \right)/\left( {{x_{\max }} - {x_{\min }}} \right)$ | (10) |
其中,
| 表 1 实验数据 |
3.3 评价标准
采用平均绝对误差(MAE)、均方根误差(RMSE)对预测结果进行评价, 计算公式如下:
| $MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{O_i} - {P_i}} \right|} $ | (11) |
| $RMSE = \sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left( {{O_i} - {P_i}} \right)} }^2}} $ | (12) |
其中,
为了验证IFA的性能, 选取Ackley函数、Sphere函数进行仿真测试. 种群数量设置为:

|
图 2 算法对Ackley函数的收敛曲线对比 |
从图2与图3看到, 针对函数Ackley与Sphere, IFA收敛速度更快, 精度更高.
为了比较性能, 分别用标准FA、GA、PSO、IFA选取SVM参数, 各优化算法得到的SVM参数如表2所示.

|
图 3 算法对Sphere函数的收敛曲线对比 |
| 表 2 优化得到的各SVM模型参数 |
3.5 实验结果与分析 3.5.1 IFA-SVM实验结果与分析
利用最优IFA-SVM参数预测2017年11月太原市两种PM2.5值:
(1)预测未来一天PM2.5浓度值;
(2)预测未来第三天PM2.5浓度值.
实验得到最终预测值, 将实际值与IFA-SVM的预测值进行对比, 结果如图4所示.

|
图 4 IFA-SVM PM2.5预测结果对比图 |
图4的结果显示, 预测太原市2017年11月的PM2.5浓度, 得到未来一天的预测结果与实际非常接近, 而未来第三天稍有偏差, 但整体变化趋势相同, 预测值与实际值的曲线拟合度很高. 此结果表明IFA-SVM模型是有效的, 该模型可以帮助预测太原市PM2.5值. 而预测未来第三天的精度比未来一天的精度低, 这主要是由于长期预测会对短期的预测错误进行积累.
3.5.2 实验结果比较与分析分别用模型GA-SVM、PSO-SVM、FA-SVM和IFA-SVM对PM2.5浓度进行预测, 预测误差结果如表3.
由表3可知, 使用四个模型对太原市2017年11月的PM2.5未来一天和第三天浓度预报后, 得到的预测误差从低到高依次是IFA-SVM、FA-SVM、PSO-SVM. 即与模型GA-SVM、PSO-SVM相比, FA-SVM的预测结果更准确, 偏离实际值较小, 而与FA-SVM相比, IFA-SVM误差更小, 即IFA-SVM模型的MAE和RMSE都是4个预测模型中最低的, 其中性能最好的IFA-SVM预测未来一天的PM2.5浓度值, MAE和RMSE分别为3.85和4.07.
| 表 3 IFA-SVM、FA-SVM、GA-SVM和PSO-SVM预测结果性能比较 |
综合考虑3.4节迭代曲线和3.5预测误差结果, 可以看到与标准FA相比, IFA收敛速度更快, 精度更高, 同时IFA-SVM PM2.5预测值也最接近实际值.
4 结论与展望针对PM2.5与影响因子间的高度非线性关系, 提出一种基于改进萤火虫寻优支持向量机的PM2.5预测模型IFA-SVM, 并以太原市未来一天和第三天的PM2.5值作为实验样本进行模型测试, 并对比GA-SVM、PSO-SVM、FA-SVM的预测效果, 经实验得到如下结论:
(1) IFA-SVM模型对未来一天和三天的PM2.5值都可以有效预测, 由于预测误差会不断积累, 一天的预测精度更高.
(2) FA能够跳出局部最优且计算简单, FA-SVM模型比GA-SVM和PSO-SVM方法预测更准确.
(3)引入邻域搜索和可变步长策略改进FA, 可加速算法收敛, 平衡局部和全局性能, 使得IFA-SVM模型预测结果更接近实际的PM2.5变化趋势, 为雾霾预测提供了一种新思路.
由于PM2.5浓度值不仅与本文所选因子有关, 还受到城市资源能耗、道路布局、空间位置等多种因素影响. 在今后的研究工作中, 尝试将这些信息和技术应用进来, 进一步提高PM2.5预测性能.
| [1] |
孙志豪, 崔燕平. PM2.5对人体健康影响研究概述
. 环境科技, 2013, 26(4): 76-78. |
| [2] |
周艳军. PM2.5的污染危害及预防对策
. 产业与科技论坛, 2013, 12(11): 114-115. DOI:10.3969/j.issn.1673-5641.2013.11.064 |
| [3] |
Jian L, Zhao Y, Zhu YP, et al. An application of ARIMA model to predict submicron particle concentrations from meteorological factors at a busy roadside in Hangzhou, China. Science of the Total Environment, 2012, 426: 336-345. DOI:10.1016/j.scitotenv.2012.03.025 |
| [4] |
郎艺超, 肖璐, Christakos G. 基于SARIMA模型和普通Kriging法对杭州市主城区PM2.5短期预测和制图
. 环境科学学报, 2018, 38(1): 62-70. |
| [5] |
程兴宏, 刁志刚, 胡江凯, 等. 基于CMAQ模式和自适应偏最小二乘回归法的中国地区PM2.5浓度动力-统计预报方法研究
. 环境科学学报, 2016, 36(8): 2771-2782. |
| [6] |
Pérez P, Trier A, Reyes J. Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile
. Atmosphere Environment, 2000, 34(8): 1189-1196. DOI:10.1016/S1352-2310(99)00316-7 |
| [7] |
Feng X, Li Q, Zhu YJ, et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation
. Atmospheric Environment, 2015, 107: 118-128. DOI:10.1016/j.atmosenv.2015.02.030 |
| [8] |
艾洪福, 石莹. 基于BP人工神经网络的雾霾天气预测研究. 计算机仿真, 2015, 32(1): 402-405, 415. DOI:10.3969/j.issn.1006-9348.2015.01.085 |
| [9] |
陈俏, 曹根牛, 陈柳. 支持向量机应用于大气污染物浓度预测. 计算机技术与发展, 2010, 20(1): 250-252. DOI:10.3969/j.issn.1673-629X.2010.01.065 |
| [10] |
Wu ZH. SVR smoggy forecast model based on data mining. International Journal of Science, 2015, 2(9): 120-125. |
| [11] |
朱霄珣, 徐搏超, 焦宏超, 等. 遗传算法对SVR风速预测模型的多参数优化. 电机与控制学报, 2017, 21(2): 70-75. |
| [12] |
戴李杰, 张长江, 马雷鸣. 基于机器学习的PM2.5短期浓度动态预报模型
. 计算机应用, 2017, 37(11): 3057-3063. |
| [13] |
杨孟英. 基于支持向量机的中文文本分类研究[硕士学位论文]. 保定: 华北电力大学, 2017.
|
| [14] |
杨海, 丁毅, 沈海斌. 基于改进萤火虫算法的SVM核参数选取. 计算机应用与软件, 2015, 32(6): 256-259. DOI:10.3969/j.issn.1000-386x.2015.06.063 |
| [15] |
Kanimozhi T, Latha K. An integrated approach to region based image retrieval using firefly algorithm and support vector machine. Neurocomputing, 2015, 151: 1099-1111. DOI:10.1016/j.neucom.2014.07.078 |
| [16] |
Ch S, Sohani SK, Kumar D, et al. A support vector machine-firefly algorithm based forecasting model to determine malaria transmission. Neurocomputing, 2014, 129: 279-288. DOI:10.1016/j.neucom.2013.09.030 |
| [17] |
王晓静, 彭虎, 邓长寿, 等. 基于均匀局部搜索和可变步长的萤火虫算法. 计算机应用, 2018, 38(3): 715-721. |
| [18] |
Wang H, Cui ZH, Sun H, et al. Randomly attracted firefly algorithm with neighborhood search and dynamic parameter adjustment mechanism. Soft Computing, 2017, 21(18): 5325-5339. DOI:10.1007/s00500-016-2116-z |
| [19] |
Yu SH, Zhu SL, Ma Y, et al. A variable step size firefly algorithm for numerical optimization. Applied Mathematics and Computation, 2015, 263: 214-220. DOI:10.1016/j.amc.2015.04.065 |
| [20] |
谢金鑫. 基于数据挖掘的雾霾天气影响因子研究[硕士学位论文]. 成都: 电子科技大学, 2014.
|
| [21] |
Zhang CH, Tian YJ, Deng NY. The new interpretation of support vector machines on statistical learning theory. Science in China Series A: Mathematics, 2010, 53(1): 151-164. |
| [22] |
Fister I, Fister Jr I, Yang XS, et al. A comprehensive review of firefly algorithms. Swarm and Evolutionary Computation, 2013, 13: 34-46. DOI:10.1016/j.swevo.2013.06.001 |
 2019, Vol. 28
2019, Vol. 28



