国家已经建立起一套以奖学金、助学贷款、贫困生资助、勤工俭学以及减免学费等方式对高校贫困学生给予资助的多元化助学政策体系. 如何利用高校各个业务系统的数据去判定高校学生的贫困程度以对助学体系提供数据佐证, 即通过数据去预测符合某些外在特征的学生属于何种程度的贫困, 是现阶段数据挖掘分析需要解决的问题.
国外的很多国家因为社会体系相对完善, 国家的税收制度能够很好地体现出每个人或家庭的整体收入状况, 可以很容易地从收入查证和个税征收中进行有效地考察, 进而得出学生家庭的整体经济状况指标并得以对贫困生进行认证. 在国内, 一些专家借鉴国外的一些现有的制度方法, 结合国内现状来完善认定体系: 罗丽琳[1]从框架设计、制度保障、技术路径和联动机制等四个方面对高校精准资助模式进行理论模型的构建与制度的创新; 穆扬等[2]提出利用先进的网络技术和成熟的地理信息系统技术, 建立高校贫困生认定新体系; 宋德昌[3]以加权算法计算三种消费指数, 得出学生经济状况综合评判结果; 段旭梅等[4]构建包括3个一级、9个二级和19个三级评价指标的层次性贫困生认定指标体系.
在数学统计和数据挖掘等手段的评定鉴别机制方面: 樊搏等人[5]使用K-MEANS算法设定阈值, 将学生分成5个级别, 判断是否属于贫困生; 张林[6]将整合处理后的学生校园卡日常消费数据作为高校家庭经济困难学生认定工作的参考依据; 史甜[7]基于Apriori算法进行一种能够面向多值属性的关联规则改进, 提高了数据挖掘效率; 王平等[8]提出了基于SOA的高校贫困生认定体系的方法; 龙钊等[9]构建了基于灰色BP神经网络的高校贫困生认定模型; 张建明[10]对数据预处理并使用C4.5算法、预剪枝、后剪枝, 分别归纳出决策树对结果进行分析选出其中较优的结果.
以上高校贫困生评价当中所运用的评价方式通常是定量、定性或者是定量与定性相结合的方式, 但定性环节的民主评议具有较多不确定性, 同时定量标准也缺乏客观依据. 贝叶斯网络因其具有多源信息综合表达、节点全部可见、双向推理、可处理不完整数据、有效表达变量间的非线性关系等优点, 已成为处理不确定性问题的重要工具, 广泛应用于智能推理、诊断、决策、预测、风险分析等方面[11,12]. 因此, 本文引入一种概率性的测度方法来解决贫困生认定中的不确定性问题, 将贝叶斯网络方法间接地通过主体的外在表现来对高校贫困生的内在不确定性进行精准测度, 为高校贫困生认定工作提供有力的支撑.
1 高校贫困生判定方案设计 1.1 现阶段环境下的贫困生判定随着新时代移动互联、云计算、人工智能、物联网等高新信息技术的发展, 借助于统一身份认证、统一门户、统一基础技术平台、统一公共数据标准的大数据共建共享机制, 利用上层各种应用系统如教务教学数据、图书借阅数据、生活消费一卡通数据等校园信息化环境中积累的数据, 对学生的个人信息、学业水平、消费习惯爱好、表现结果等分析挖掘, 得到贫困学生行为的基本行为特征, 可以为智慧校园下高校贫困省认定工作提供有力支撑.
1.2 贫困生的界定特征构建通过对高校学生资助政策和校园大数据的分析, 探索应用大数据方法判断贫困生等级. 首先将学生分为四个等级: 特困生、贫困生和非贫困生, 其次根据往年认定的贫困生历史数据, 取三分之一作为训练样本, 采集教务系统中的学生学业水平数据、参考图书管理系统中的借阅数据、分析一卡通系统中学生的生活消费数据, 重点挖掘学生在食堂的饮食记录数据, 如吃饭次数、平均消费金额、节假日或非饮食高峰期消费情况等, 然后按照侧重消费能力的同时借鉴学习上进程度并来对学生的贫困等级进行预测, 将预测结果与贫困生资助系统中的数据进行匹配, 最后利用贝叶斯网络技术构建反映各种数据因素与贫困生等级之间因果关系及其相互影响的贝叶斯网络模型, 进一步对高校贫困生的界定进行预测评价, 以期提供更加准确、客观的贫困生信息判定理论依据.
2 构建高校贫困生等级预测模型 2.1 高校贫困生预测的贝叶斯网络模型在现实生活中, 由于存在多种不确定性因素, 如根据先验知识构造贝叶斯网络的主观性、训练样本集的局限性(如样本的容量、样本数据的缺失情况)等, 使得认知模型的构建、推理、结果的反馈、模型的再学习将是一个不断循环和完善的进化过程, 这样才能最终使得认知模型能够尽可能准确地反映客观现实[13,14]. 本文利用此思想, 提出了一种基于贝叶斯网络的高校贫困生等级预测模型的构建方法, 如图1所示.
2.2 高校贫困生预测的贝叶斯网络拓扑结构贝叶斯网络模型的过程为: 首先通过给定的样本数据, 建立贝叶斯网络的拓扑结构和结点的条件概率分布参数, 这往往需要借助先验知识和极大似然估计来完成. 然后在贝叶斯网络确定的结点拓扑结构和条件概率分布的前提下, 使用该网络对未知数据计算条件概率或后验概率, 从而达到诊断、预测或者分类的目的[15,16].
为了要建立一个好的拓扑结构, 通常需要不断迭代和改进才可以, 步骤如下:
1) X是网络中节点的集合,
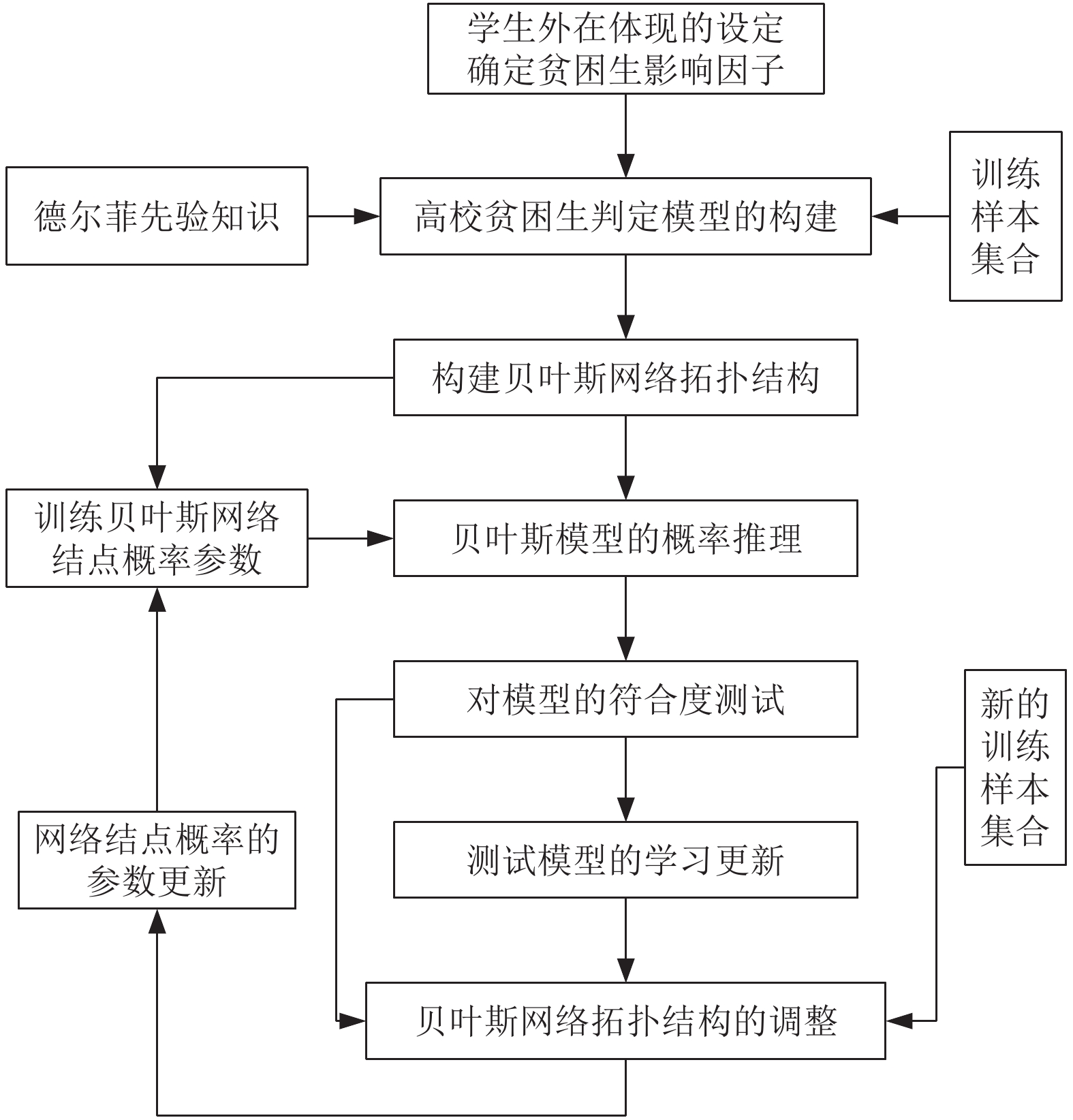
|
图 1 高校贫困生判定模型的构建方法 |
2) 确定每个网络参数
| $P\left( {{X_1},{X_2}, \cdots, {X_n}} \right) = \prod\limits_{i = 1}^n {p\left( {{X_1}{\rm{|}}{X_2}, \cdots {X_n}} \right)} {\rm{ = }}\prod\limits_{i = 1}^n {p\left( {\pi {X_i}{\rm{|}}\left( {{X_1}} \right)} \right)} $ |
3) 贝叶斯网络蕴涵了条件独立性假设, 即给定一个节点的父节点集, 该节点独立于它的所有非后代节点. 因此分析每个网络参数
4) 完成贝叶斯网络的DAG(有向无环图)结构, 也就是高校贫困生预测模型的贝叶斯网络拓扑结构, 如图2所示[17,18].
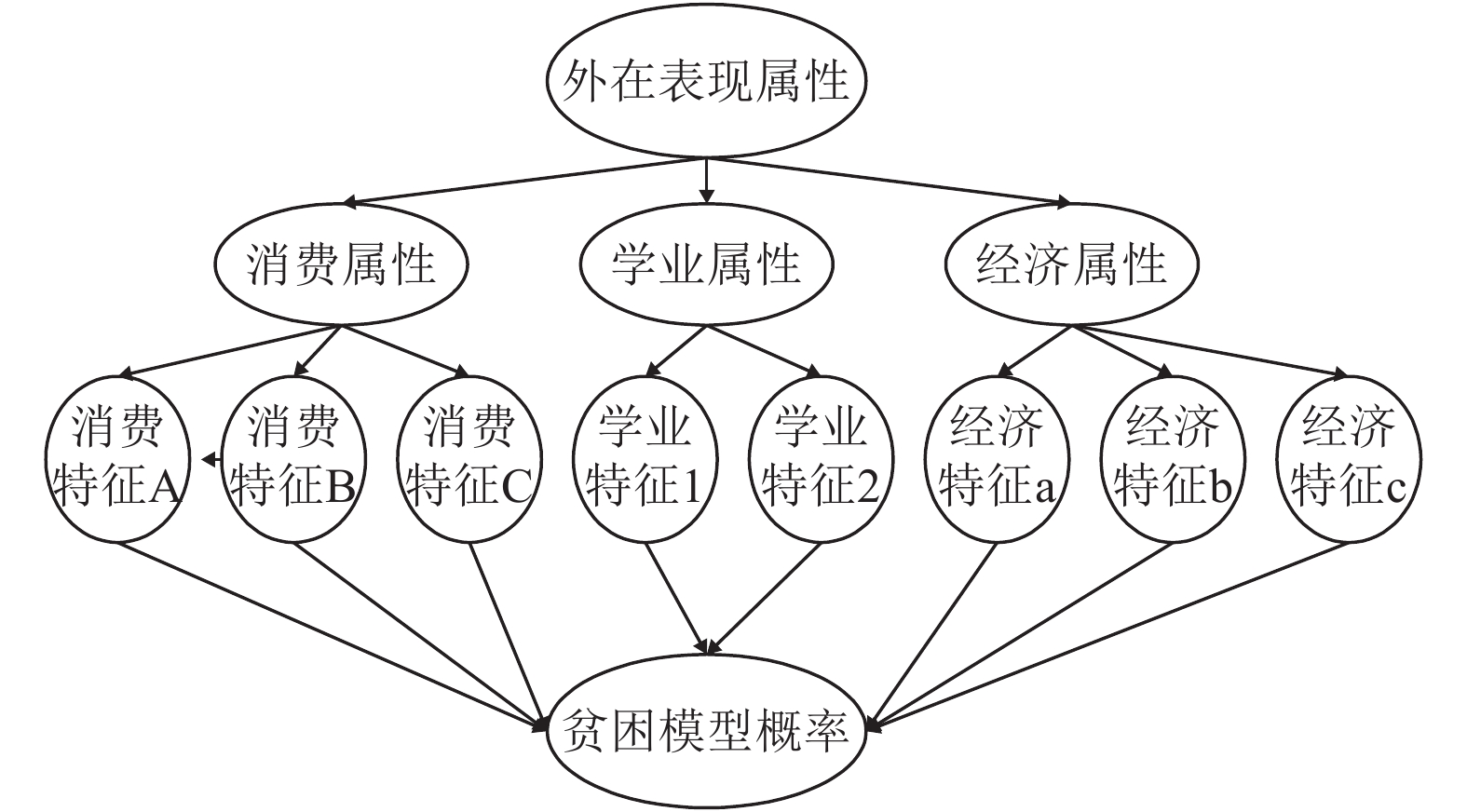
|
图 2 贫困生判定的贝叶斯网络拓扑结构 |
构建完成贫困生预测的贝叶斯网络拓扑结构后, 将从各种应用系统获得到的跟贫困生相关的信息数据组成训练样本数据集, 根据这些训练样本去进行网络节点的概率分布学习.
2.3 贝叶斯网络节点参数学习贝叶斯网络参数学习是在给定贝叶斯网络拓扑结构的情况下, 通过训练样本数据确定相关变量间的条件概率分布. 参数学习可以通过专家先验知识来为网络节点分配赋值[19], 形成初始的概率分布. 针对样本数据完整或数据不完整情况下分析贝叶斯网络参数学习方法.
在训练样本数据完整的情况下, 采用最大似然估计(MLE)方法来学习贝叶斯网络参数. 在高校贫困生预测贝叶斯模型中, 假设各样本满足统计学中的独立同分布假设, 数据K由样本(K1, K2,…, Km)组成, P(X)表示所有节点变量的联合概率密度, 已知完整的训练样本集K, 参数向量θ的似然函数为:
| $L\left( {\theta |{\rm K}} \right) = P\left( {{\rm{K|}}\theta } \right) = \prod\limits_{i = 1}^m {p\left( {{\rm{K|}}\theta } \right)} $ |
对似然函数
| $l\left( {\theta |{\rm K}} \right) = \log L\left( {\theta |{\rm K}} \right) = \log \left( {\prod\limits_{i = 1}^m {p\left( {{{{K}}_i}{\rm{|}}\theta } \right)} } \right) = \sum\limits_{i = 1} {\log } p\left( {{{{K}}_i}{\rm{|}}\theta } \right)$ |
在训练样本不完整的情况下, 假设样本数据是随机缺失的, 即一个变量值的缺失与它的实际取值无关, 在贫困生预测贝叶斯模型中, 运用期望最大化(EM)算法. 假设K=(K1, K2,…, Km)是样本数据, 对其中任一样本Kl, 设Xl是Kl中所有缺失变量的集合. 设θt是关于参数θ的当前估计, Kt是基于θt将K修补后得到的碎全完整数据, 定义θ的基于Kt的对数似然函数为:
| $l\left( {\theta |{{\rm K}^{{t}}}} \right) = \sum\limits_{l = 1}^m {\sum\limits_{{x_l} \in {X_l}} {P\left( {{X_l} = {x_l}|{K_l},{\theta ^t}} \right)} } \log P\left( {{{{K}}_i},{X_l} = {x_l}|\theta } \right)$ |
在EM的第t次迭代过程中, E-步骤计算期望对数似然函数
贝叶斯网络推理是利用贝叶斯网络模型结构及其参数在给定样本证据后计算某些网络结点取值的概率过程. 本文鉴于网络结构中变量基本可以观察到且取值完整, 选用MAP(最大后验算法)[21]计算变量的边缘概率及后验概率, 最大后验算法与最大似然估计相比最明显的区别就是考虑了先验概率影响因素[22].
假设高校学生主体外在表现组成的信息集合为I(I1, I2,…,IM)
, 贫困生的确定信息集合为H(H1, H2,…, HN)
, 通过贝叶斯网络模型的概率推理就是计算P(Hi|I)
, 确定出概率值最大的某种信息类别Hi作为第一次推理结果, 在此基础上将其作为第二次推理结果, 以此类推获取贫困生概率值. 该概率值标明贫困生可以得到精准判断的可能性, 在此可以根据定额指标设置合理的阈值ϼ, 若
高校贫困生预测模型能否达到一定的精确度以满足学生助学部门的实际要求, 还需对此模型进行准确型和有效性比对. 具体方法是将训练样本数据根据贝叶斯网络模型得出的训练结果与部分实际值进行比对, 若比对效果符合要求, 则本模型的构建和预测完成; 反之, 则通过调整贝叶斯网络拓扑结构或增加训练样本集的样本容量、重新选取各级指标等方法进行该模型的重新构建和推理学习.
3 应用分析与实证本文通过某高校2016–2017年度各种应用系统如教务教学数据、图书借阅数据、生活消费一卡通数据、学生家庭基本情况数据等智慧校园信息化环境中积累的数据, 选取预测因子, 利用贝叶斯网络技术构建反映各预测因子与贫困生确定指标及其相互影响的贝叶斯网络模型, 对某高校的贫困生精准判定进行预测和评价.
3.1 预测因子的选取和数据的清洗高校贫困学生的成因情况复杂, 但基本因素多集中在家庭经济情况、生源经济水平、家庭劳动力状况等, 在学校导致学生的外在表现主要在消费能力水平、消费习惯、学业水平、学习主动力等方面[23], 参考文献[10–12]中的贫困生体系指标因素模型, 依据德尔菲专家知识方法, 选取具有典型特征的学生餐饮消费次数、餐饮消费平均额度、餐饮消费标准偏差、学生家庭劳动力数量、生源地经济水平、家庭重慢病人口数目、学生学业水平程度、学生图书借还数等影响因子对学生贫困程度进行判定预测.
某高校在校生数量超过万人, 从各种应用平台中抽取的数据特别是一卡通的餐饮数据相当庞大, 比如仅仅一个月的学生一卡通餐饮SQL数据记录总数就超百万条, 囊括餐厅、冷饮、超市、浴池甚至社区医院等所以消费场所. 庞大的数据量必须进行清洗整形, 首先利用SPSS大数据统计软件进行数据个案及变量合并, 然后依据学生学号进行分类汇总消费次数、每次平均消费额和消费标准偏差等因子, 结合EXCEL软件的VLOOKUP、SUMIF、COUNTIF等函数将学生家庭劳动力数量、生源地经济水平、家庭重慢病人口数目、学生学业水平程度、学生图书借还数等其他因子数据统一同步建表, 清理无效噪声记录数据后得到完整的样本数据共10 115组. 这些组样本数据分为训练数据和验证数据两部分, 其中训练数据用于构建贝叶斯网络模型及推理学习, 验证数据用于模型实证及预测分析.
3.2 数据离散化和贝叶斯网络参数学习贝叶斯网络方法需要处理样本数据的离散属性, 结合前文文献中的预测因子, 确定贫困生认定体系和各因子离散化后的标准属性值如表1所示. 其中将各因子属性值分为四个区间等级, 表中的助学补助金额指数四个区间分别对应高校学生贫困程度为特困、贫困、一般和非贫困.
| 表 1 高校贫困生预测因子标准属性离散值表 |
贝叶斯网络节点的概率参数学习训练也就是要求输入贫困程度不同的学生样本数据来对参数进行训练, 样本容量的数量决定着参数训练取值的真实情况拟合度. 在前述数据清洗后得到的样本数据基础上, 将其中8106组数据从EXCEL中导入MATLAB软件平台, 在MATLAB软件中按照表1属性区间值仿真出样本值的贝叶斯网络结构后, 结合微软贝叶斯网络工具箱绘出网络结构并进行推理, 分别计算各因子指标的概率, 各节点概率参数值如图3所示.
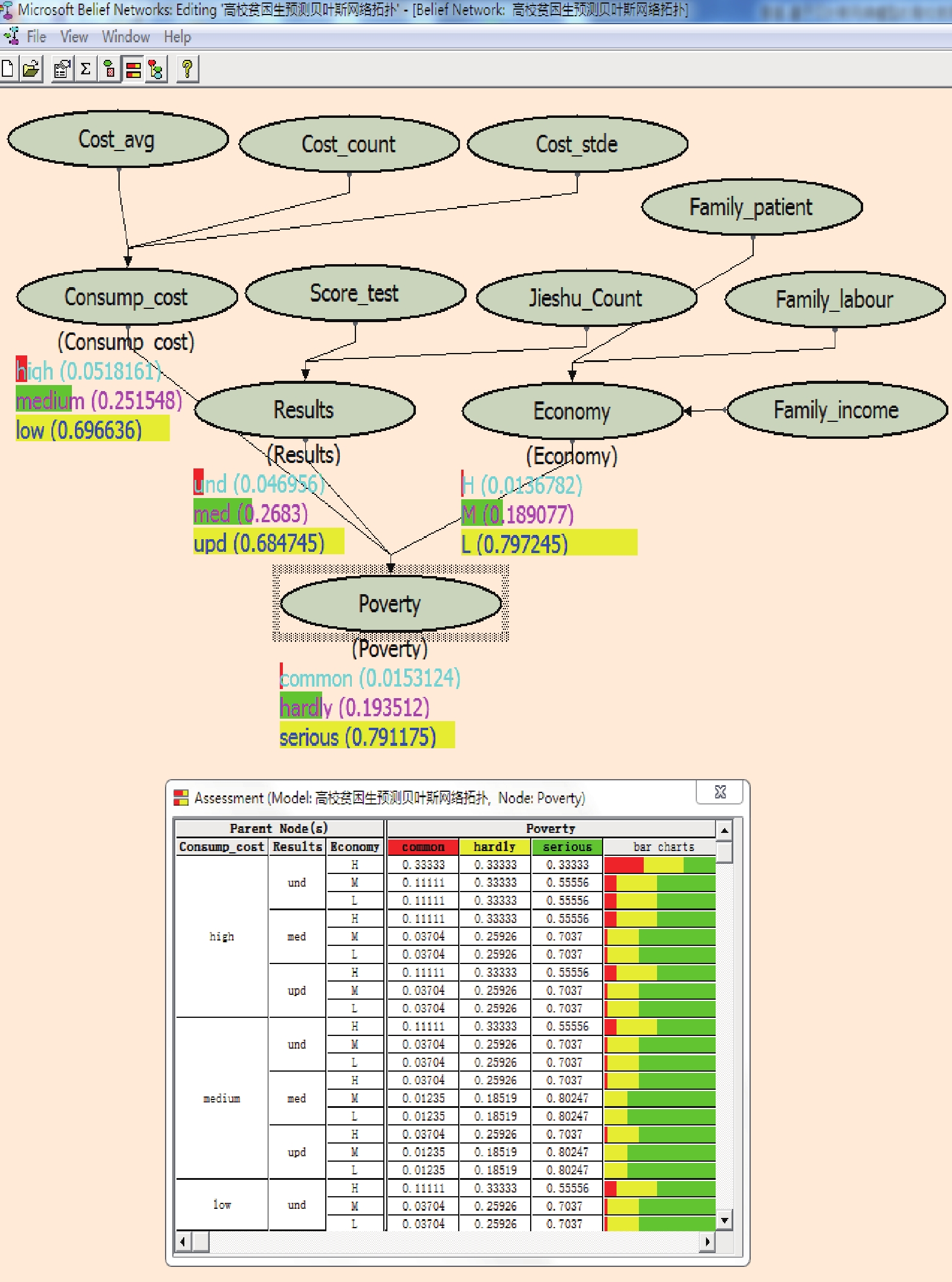
|
图 3 贝叶斯网络结构概率参数 |
由图3贝叶斯网络结构中有向边的指向关系可以看出, 预测因子间存在着因果影响关系, 消费次数、消费平均额度和消费标准偏差影响着消费水平Consump_cost, 加权平均成绩和图书借还次数影响着学业水平Results, 家庭劳动力数量、生源地人均GDP和家庭病困人口数影响经济水平Economy, 消费水平Consump_cost、学业水平Results、经济水平Economy综合影响决定着学生的贫困程度Poverty. 鉴于网络结构中变量基本可以观察到且取值完整, 选用MAP(最大后验算法)进行贝叶斯网络参数学习, 计算变量的边缘概率及后验概率.
3.3 模型的有效符合度测试高校贫困生判定模型的重点是判别哪些样本数据更符合补助标准, 至于补助等级之间的差别可以通过专家知识法比如通过学生民主推举等方式来确定, 因此主要是选取未参与训练的1915组数据中的不同助学补助标准数据来验证模型的有效符合度, 从中随机选取25个特困生样本数据和25个非贫困生样本数据, 利用模型推理这50个样本数据的概率分布, 求得样本的贫困程度水平值并排序, 最后对比排序结果来分析模型的有效符合度. 测试样本的概率计算结果如表2所示.
| 表 2 测试样本集的拟合概率结果 |
该概率值结果标明贫困生可以得到精准判断的可能性, 在此根据定额指标设置合理的阈值ϼ=0.65, 也就是说若P(Hi)≥0.65, 则说明该学生有超出阈值ϼ的大概率P(Hi)值得以精准判定其为贫困生. 根据这个阈值标准, 可以统计出本次测试正确率为86%. 阈值需根据实际要求和实际情况来确定, 因为测试正确率随着阈值标准而变化.
增加样本数据数量至300组, 将通过贝叶斯网络模型推理出的数据结果与实际补助情况的数据在SPSS中进行独立样本T检验[24], 对预测值和实际值进行对比验证结果如图4, 可以看出这300组数据的预测值和实际值的P值, 也就是图中的Sig值为0.339大于0.05, 说明两组方差齐性, Sig(双侧)值为0.207, 说明数据之间平均值没有显著差异, 亦表明本文的基于贝叶斯网络模型对高校贫困生的判定具有较高的预测精度.
4 结论将学校的标准与学生的户籍信息进行二者的相互结合后, 进而由地方民政部门出具相关的贫困证明材料, 然后把所获取的信息综合到一起来对学生进行贫困度的认定与评价.
机器学习虽然有着在训练数据所需要的时间较长、对所获取知识的理解上不够智能的不足之处[25]. 但是机器学习不强调模型的结构, 只需根据输入的数据特征就可检验预测的精确度[26]. 贝叶斯网络概率推理旨在充分挖掘模型潜在因素, 实现正确预测[27]. 本论文以高校贫困生的各种外在表现数据, 特别是清洗过的日常消费数据为依据, 构建贝叶斯网络模型, 通过网络参数的学习推理确定模型结构个结点的概率参数, 在此基础上将测试样本与训练样本进行拟合度对比, 从而得出贝叶斯网络推测模型. 从测试结果看, 证明了基于贝叶斯网络的高校贫困生测试模型对高校贫困生的量化定性具有一定的可行性.

|
图 4 SPSS对300组数据的独立样本T检验结果 |
贝叶斯网络构建高校贫困生判定模型还应有其他需要考虑之处: 一是样本数据的完整型需进一步完善, 比如随着扫码支付的普及, 这部分消费数据没有与高校的一卡通数据进行完整合并; 二是部分数据有进一步细化的必要, 如学生三餐的不同消费水平对贫困程度的判定有着一定影响; 三是可以用BP神经网络模型与贝叶斯网络模型进行预测精度深入对比等等, 这需要在模型后续细化中逐步解决.
| [1] |
罗丽琳. 大数据视域下高校精准资助模式构建研究. 重庆大学学报(社会科学版), 2018, 24(2): 197-204. DOI:10.11835/j.issn.1008-5831.2018.02.017 |
| [2] |
穆扬, 张永福. 高校贫困生认定体系的重构. 西北工业大学学报(社会科学版), 2017, 37(1): 70-73, 77. |
| [3] |
宋德昌. 基于校园卡的学生经济状况评价方法研究. 中山大学学报(自然科学版), 2009, 48(S1): 9-11. |
| [4] |
段旭梅, 胡梦英, 钟俊男. 构建高校贫困生认定的数学模型及其应用. 吉林省教育学院学报, 2015, 31(5): 150-151. DOI:10.16083/j.cnki.1671-1580.2015.05.067 |
| [5] |
樊搏, 姜玉国. 基于数据挖掘的贫困生认定辅助系统设计. 软件开发与应用, 2015, 14(12): 134-135. |
| [6] |
张林. 基于差分隐私保护技术的高校贫困生认定系统设计. 计算技术与自动化, 2017, 36(3): 151-156. DOI:10.3969/j.issn.1003-6199.2017.03.031 |
| [7] |
史甜. 数据挖掘在高校贫困生认定系统中的应用研究[硕士学位论文]. 西安: 西安科技大学, 2017. 6.
|
| [8] |
王平, 龚文涛. 基于SOA的高校贫困生认定体系的研究. 微型电脑应用, 2015, 31(10): 55-56, 59. |
| [9] |
龙钊, 梁静, 蒋志成. 基于灰色BP神经网络的高校贫困生认定模型. 教师, 2015(23): 125-126. |
| [10] |
张建明. 基于数据挖掘的高校贫困生认定系统设计和分析[硕士学位论文]. 南京: 东南大学, 2015. 6.
|
| [11] |
Jensen F. An Introduction to Bayesian Networks. New York: Springer, 1996.
|
| [12] |
Broom BM, Do KA, Subramanian D. Model averaging strategies for structure learning in Bayesian networks with limited data. BMC Bioinformatics, 2012, 13(Suppl 13): S10. |
| [13] |
乔秀全, 李晓峰, 廖建新. 基于贝叶斯网络的业务上下文认知模型构建方法. 电子与信息学报, 2008, 30(2): 464-467. |
| [14] |
Huang S, Li J, Ye JP, et al. A sparse structure learning algorithm for Gaussian Bayesian network identification from high-dimensional data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1328-1342. DOI:10.1109/TPAMI.2012.129 |
| [15] |
De Campos LM, Castellano JG. Bayesian network learning algorithms using structural restrictions. International Journal of Approximate Reasoning, 2007, 45(2): 233-254. DOI:10.1016/j.ijar.2006.06.009 |
| [16] |
陈友玲, 张岳园, 凌磊, 等. 基于贝叶斯网络的个体隐性知识测度方法研究. 计算机应用研究, 2019, 36(6). DOI:10.3969/j.issn.1001-3695.2017.12.0799 |
| [17] |
李硕豪, 张军. 贝叶斯网络结构学习综述. 计算机应用研究, 2015, 32(3): 641-646. DOI:10.3969/j.issn.1001-3695.2015.03.001 |
| [18] |
化虎蝶, 王晨祥. 基于贝叶斯网络的大连市空气质量预测与诊断. 安全与环境工程, 2018, 25(1): 58-63. DOI:10.13578/j.cnki.issn.1671-1556.2018.01.010 |
| [19] |
范敏. 基于贝叶斯网络的学习与决策方法研究及应用[博士学位论文]. 重庆: 重庆大学, 2008.
|
| [20] |
张连文, 郭海鹏. 贝叶斯网引论. 北京: 科学出版社, 2006.
|
| [21] |
Leray P, Francois O. Bayesian network structural learning and incomplete data. International and Interdisciplinary Conference on AKRR. Espo, Finland. 2005.
|
| [22] |
Zheng MK, Ming XG, Zhang XY, et al. MapReduce based parallel bayesian network for manufacturing quality control. Chinese Journal of Mechanical Engineering, 2017, 30(5): 1216-1226. DOI:10.1007/s10033-017-0179-0 |
| [23] |
黄良斌. 高校贫困生认定标准与认定模型研究. 职业教育研究, 2012(4): 11-12. |
| [24] |
张文彤, 邝春伟. SPSS统计分析基础教程. 2版. 北京: 高等教育出版社, 2011.
|
| [25] |
陈小燕. 机器学习算法在数据挖掘中的应用. 现代电子技术, 2015, 38(20): 11-14. DOI:10.16652/j.issn.1004-373x.2015.20.030 |
| [26] |
黄卿, 谢合亮. 机器学习方法在股指期货预测中的应用研究——基于BP神经网络、SVM和XGBoost的比较分析. 数学的实践与认识, 2018, 48(8): 297-307. |
| [27] |
翟社平, 郭琳, 高山, 等. 一种采用贝叶斯推理的知识图谱补全方法. 小型微型计算机系统, 2018, 39(5): 995-999. |
 2019, Vol. 28
2019, Vol. 28


