网络技术的飞速发展和各种电子设备成本的下降为当今信息传播的爆炸式发展提供了契机, 我们现在接触到的海量信息均依托于不同的信息载体. 其中图片和视频是日常生活中非常重要和直接的两种信息来源, 在今天的社交活动、娱乐活动中扮演着重要的角色. 这些视觉数据除了图形本身传递的信息外, 往往还包含文本元素, 这些文本能够更加直接的传递信息, 也因此需要被研究人员重点关注.
由于近年来深度学习算法的发展, 场景文本识别技术取得了丰硕的成果[1]. 目前深度学习中的场景文本识别主要基于两种思路. 第一种是将“检测”和“识别”两个模块的算法替换成深度模型, 利用深度模型本身的优势解决问题; 另一种是针对短文本行或单词文本, 将检测和识别两部分在深度网络中加以融合, 实现不依赖于切分的序列化文本识别. 两种思路都在场景文本识别任务中取得了良好效果, 但是却在落地产品时遇到了瓶颈.
深度神经网络(DNN)在众多领域中取得了非常好的效果, 这离不开硬件条件的支持. 但由于深度学习方法的计算复杂度过大, 导致算法对硬件环境(GPU、TPU等)的要求过高[2]. 而真正在使用一个深度模型时, 一旦脱离了GPU的支持, 运算速度就会降低一个数量级以上, 导致很多任务中的复杂模型无法实时运行[3–5], 很多当下流行的如手机、摄像机等能源储量低、计算能力弱的设备无法有效使用深度神经网络模型[6–9].
因此人们开始对计算方式进行改进优化, 通过特定的处理方法, 降低深度模型在运行时所需的乘法运算量, 二值网络[10,11]因其在速度、能耗、内存占用等方面的优势日益被关注. 近两年来, 单纯加入二值化操作的网络主要有二值权重网络和二值神经网络两种方法. 二值权重网络(BWN)[12,13]是一种只针对神经网络系数二值化的算法. BWN只关心系数的二值化, 并采取了一种混和的策略, 构建了一个混有单精度浮点型中间值与二值权重的BinaryConnect网络, 它把原始全精度浮点权重强行置为–1、+1两个浮点数, 同时不改变网络的输入和层之间的中间值, 保留原始精度. 权重取值的特点使得原本在神经网络中的乘法运算可以被加法代替, 大大地减少了计算量. 而二值神经网络(BNN)不仅对权重做二值化, 也对网络中间每层的输入值进行二值化, 它将二值浮点数“–1”、“+1”分别用一个比特“0”、“1”来表示, 这样原本占用32个比特位的浮点数现在只需1个比特位就可存放. 然而大量的实验结果表明, BNN在大规模数据集上的效果很差. 它们在提升速度、降低能耗、减小内存占用等方面存在巨大的可能性, 但这样做会对识别精度造成一定的影响. 只有做到保持原有精度, 二值网络、量化网络的思路才能够真正在应用中得以实现.
单纯使用BWN或BNN确实会对深度网络模型造成较大的精度损失. 同或网络(XNOR-net)[14]的提出主要就是为了解决二值网络精度损失的问题. XNOR-net是一种针对CNN的简单、高效、准确近似方法, 核心思想是: 在BNN的基础上, 针对二值化操作给每一层数据造成的误差, 引入最佳的近似因子, 以此来弥补二值化带来的精度损失, 提高训练精度的同时保持BNN在速度和能耗方面的优势.
随机量化算法的核心在于训练过程中考虑到量化误差的因素, 只对误差较小的部分权重采用一定的概率进行量化, 其他权重则保留原始精度, 这样对混合模型的训练达到收敛后, 再去量化剩余的权重, 逐步增加量化比例, 直到模型完全收敛, 接近原始精度的准确率. 随机量化网络算法能够训练得到比BWN更高的准确率, 但是对于BNN却没有做更进一步的分析, 也没有能够利用XNOR-net这一算法给模型带来准确率方面的提升, 鉴于它的有效性, 我们需要更好的将其应用到BNN中.
在文本识别任务中采用XNOR-net算法可以实现CPU条件下5倍以上的加速, 采用二值模型能够实现64倍的峰值内存占用压缩, 这就基本实现了低配硬件条件下深度模型的实时运行. 虽然XNOR-net算法的目的是为了弥补二值网络造成的识别精度下降, 但是仅采用这一算法依然不能有效的保证深度网络训练模型的准确率.
为了解决上述问题, 提升二值网络的训练精度, 本文提出了二值网络的“分阶段残差二值化”优化算法. 实验表明, 该算法能显著提升二值网络训练效果而不会增加相关网络在测试过程中的计算量, 从而保持了二值网络速度快、空间小、能耗低的优势. 本文使用整合得到的二值深度框架对文本识别任务展开训练, 主要工作包括: 将随机量化网络算法与XNOR-net相结合进行分析与改进, 并对提出的“分阶段残差二值化”算法进行研究与评估. 通过对上述算法的实验与改进, 得到接近全精度神经网络的识别准确率.
1 相关工作概述本节将对随机量化网络和高阶残差量化网络进行概述, 并对这两种网络目前存在的问题进行简要的分析. 首先介绍了随机量化网络算法; 其次将随机量化的思想与XNOR-net进行结合, 得到“带有近似因子”的随机权重二值化网络; 接着, 进一步对“随机”的优缺点进行分析, 基于卷积计算的结构进行合理改进得到“确定权重二值化网络”; 最后, 对高阶残差量化网络进行了简要的概述和分析.
1.1 随机量化网络介绍随机量化网络是一种针对BWN的训练优化算法, 算法设计的出发点是基于对二值化误差的分析. 权重在二值化过程中被强制引入了较大误差, 这一误差将导致总体损失非常大, 从而致使网络的训练过程极不稳定, 无法收敛到最优结果, 这也就是二值网络准确率较差的原因. 随机量化网络则试图减小损失过大带来的训练过程的剧烈震动, 这与调小学习率等训练技巧不谋而合. 图1是随机量化流程图, 具体的实现过程如下文.
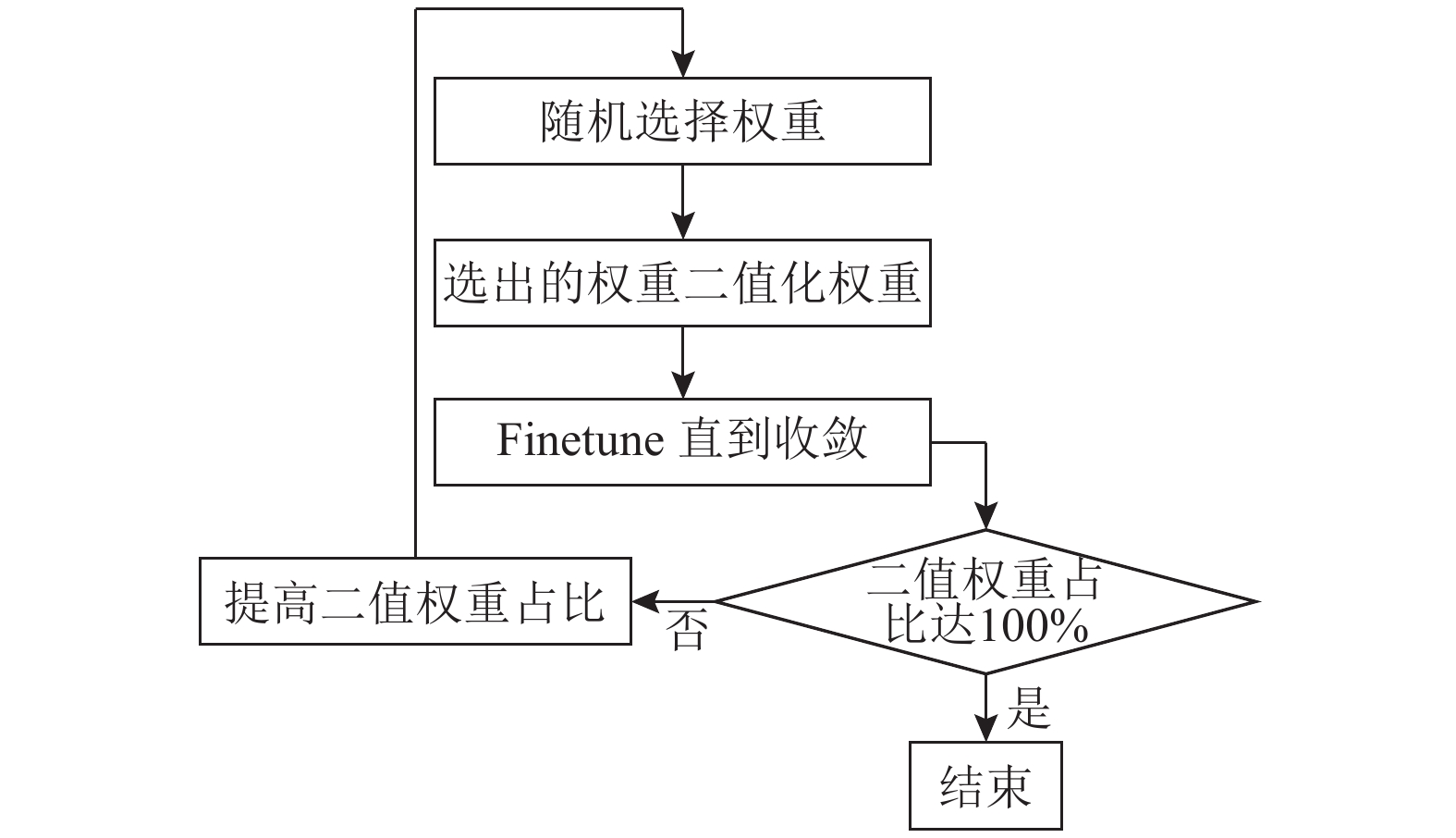
|
图 1 随机量化流程图 |
1) 预训练. 将二值化比例置0, 保留全部的原始精度权重, 以得到一个准确率较高的预训练模型.
2) 随机选取二值化权重. 提高二值化比例, 使得一部分训练中的权重会被二值化. 如何选取这些权重呢?首先统计二值化给不同权重带来的误差大小, 按“误差越小, 被二值化的几率越大”原则, 用“轮盘赌”的方式随机选取一部分权重进行二值化训练. 训练过程跟普通BWN一样.
3) 将提高了二值化比例的网络在预训的模型上进行finetune, 直到训练的准确率达到与之前全精度网络模型接近的水准.
4) 在finetune成功的模型上继续提高网络二值化的比例, 重复2)、3)的步骤, 直到整个网络中的模型权重被二值化的比例达到100%, 且finetune的结果达到可接受范围.
以上就是随机量化网络的具体实现, 其中需要注意的点在于“随机”的概念, 即“中间每次训练的过程中被二值化的权重并不固定”. 这样做会造成前期finetune的困难, 因为被影响的权重较多, 需要大量权重基本调整好之后网络才会收敛的比较好; 但是等到训练中后期, 大部分的权重已经被调优到了最佳位置, 这时候网络的finetune会非常容易.
1.2 随机权重二值化及近似因子XNOR-net是一种有效的二值训练精度优化算法, 在这里我们考虑将“随机量化”这一思想应用在XNOR-net权重二值化中, 进一步提升二值网络的训练精度. 随机量化网络在实现时并不会具体到每个权重, 而是以整个通道为单位来操作的, 而XNOR-net算法的处理也是通道级别的, 这就为我们研究如何将两种训练优化算法合理融合提供了便利.
要将XNOR-net的权重近似推导应用于随机量化网络, 最重要的是要解决两点问题: 一是在求近似因子
解决第一个问题则必须要明确一点: 出于实现简单的考虑, 随机量化网络并非针对每个权重都去判断是否二值化, 而是通过同一个输出通道上的一组权重的总误差来决定的. 而我们在实现XNOR-net算法时也是在一组通道上求得一个近似因子
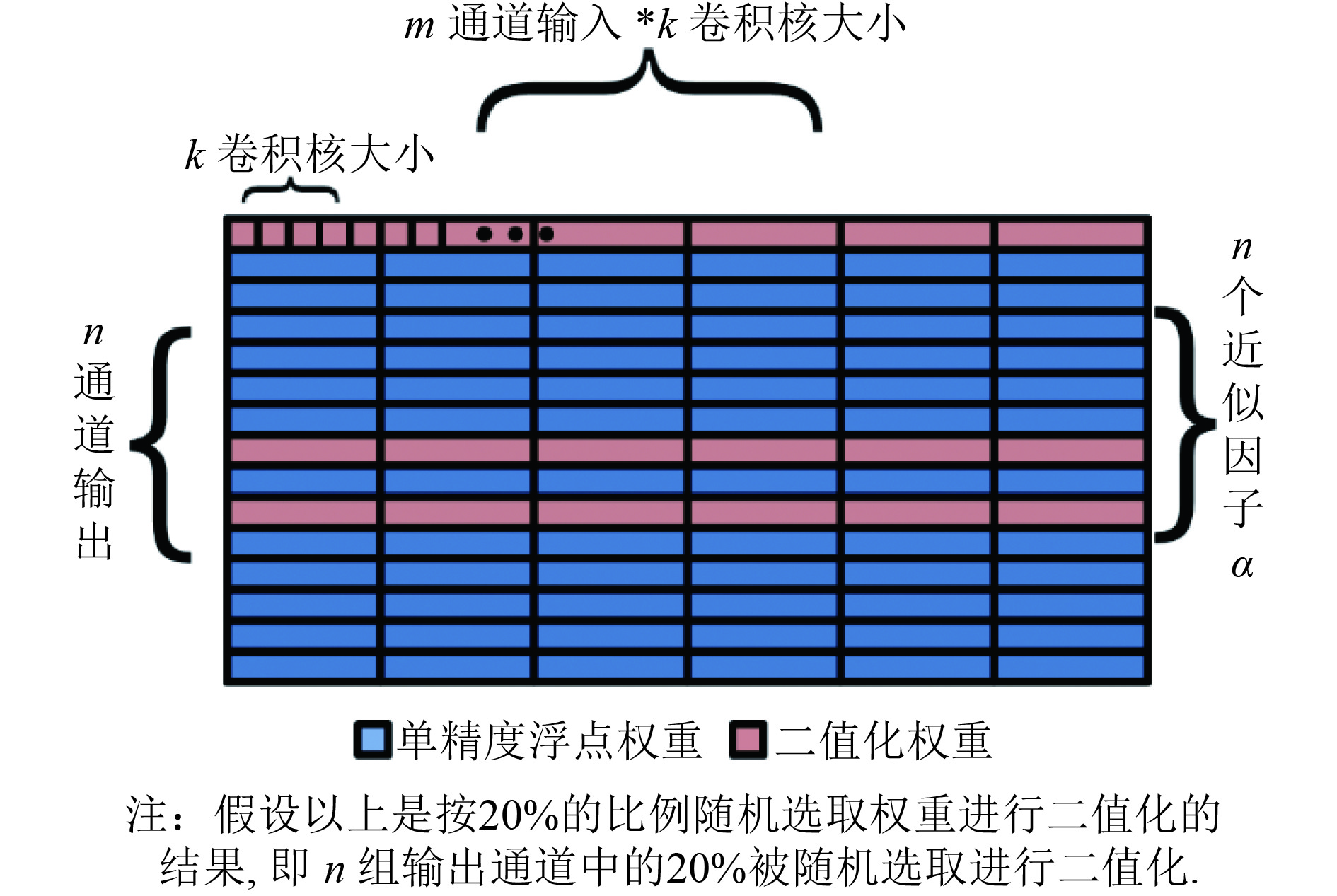
|
图 2 权重矩阵随机求取
|
有了二值化的选取规则, 还需要解决的第二个问题是: 存在近似因子时如何确定量化选取通道的概率. 直观的, 我们可以得到如下的量化误差统计公式:
| $e\_XNO{R_i} = \frac{{\parallel {w_i} - Q\_XNO{R_i}{\parallel _1}}}{{\parallel {w_i}{\parallel _1}}} = \frac{{\parallel {w_i} - {B_i} * {\alpha _i}{\parallel _1}}}{{\parallel {w_i}{\parallel _1}}}$ | (1) |
以上我们就完成了对“带有近似因子的随机权重二值化网络”的研究, 具体来说, 在随机量化网络上加入XNOR-net的近似因子方法的实现过程可以总结为4个步骤:
1) 计算每一组通道权重的近似因子
2) 求出每组输出通道上添加了近似因子后的权重量化、二值化误差, 计算的定量表达见式(1);
3) 根据量化误差, 计算每个通道的权重被进行二值化的概率;
4) 以概率大小为依据, 采用轮盘赌的方式选取可以进行权重二值化的通道, 选中的通道被二值化. 在训练时, 需要二值化这些通道的权重并乘上相应的近似因子
为了证明根据之前的介绍, 我们知道在随机量化权重中加入近似因子这一优化对于实现来说会造成比较大的额外成本, 这主要是因为量化通道的选取过程是“随机的”, 而每个通道被选取的概率也是基于对二值化误差的计算得到的. 因此, 每次对二值化通道的选取过程都需要对所有通道的二值化误差进行求解, 而当引入XNOR-net算法中的近似因子操作后, 又增加了求每组通道上近似因子一项, 额外的计算成本变得更高, 实现更加复杂.
本节提出的改进办法是将“随机”改为“确定”, 只在初始时对每个通道计算一次二值化误差, 然后确定进行二值化的通道. 即每次训练给出确定的二值化通道, 这样可以避免每次都对不需要量化的通道进行计算, 在有效节省训练时间的同时, 也简化了深度学习框架中对这一算法的实现过程. 由于“随机量化网络”结合了误差的大小来选取量化通道, 而我们“确定二值化通道”的方法也在初始时利用了这一优点, 因此具有单次迭代训练比较容易收敛、后期迭代比前期迭代更快收敛的特点.
但是“确定权重二值化”的方法确实也存在一定的问题. 我们知道, “确定”方式可以有效地节省训练时间, 在训练过程中, 随着训练轮数的增加, 误差较大的通道也能逐渐收敛. 虽然不能保证每次训练都对误差最小的一些通道进行二值化, 但是网络最终都会收敛, 因此是否每次都选择误差最小的一些通道对训练结果影响甚微.
“阶段量化”则是一种纯线性的训练模式, 由于只在初始时对每个通道计算一次二值化误差, 每次训练只二值化固定的通道, 其他通道不会出现二值化, 因此整体上看每次迭代的训练难度只与二值化比例有关. 这样做虽然会导致每次二值化比例提升后都需要对所有新产生的二值化权重进行调整, 看上去后期训练收敛的过程会相对变慢, 但是因为二值化的选取变成了确定式的, 使得前期训练收敛变得相对更容易, 因此整体上看并不会增加训练的难度. 改进后的阶段量化方式示意图如图3所示.

|
图 3 改进后的阶段量化方式示意图 |
实验表明, 采用了这一改变后的随机量化网络, 也就是“确定权重二值化网络”, 通过更新二值化的比例并进行finetune, 不仅可以有效提升二值化通道选取的效率, 同时依然能够得到与全精度的预训练模型准确率相近的二值网络模型. 因此, 本文继续在这一思路上展开研究, 将“确定”的思想推广到BNN乃至整个XNOR-net.
1.4 高阶残差量化网络网络量化分为输入量化和权值量化两种. 而同时将输入和权值量化会造成网络精度的大幅下降. 针对这个问题, 高阶残差量化HORQ方法提出了一种针对输入的高阶残差二值量化的方法, 既能够利用二值化计算来加快网络的计算, 又能够保证训练所得的二值化网络模型有较高的准确率.
HORQ方法可以作为一个基础的二值量化的方法用于网络的输入二值化中, 能够在保证网络模型精度的前提下, 利用二值量化的技术提升网络的计算速度, 而且同时可以根据实际的硬件需要来调整残差阶数以适应需求.
HORQ可以看做是XNOR-net的改进版, 要对权重和输入进行高阶残差近似, 先按照 XNOR-net的方法对权重和输入进行一阶二值近似, 下面以输入为例进行高阶残差近似的分析:
| $X \approx {\beta _1}{H_1}$ | (2) |
随后, 就可以由此定义输入残差张量, 可以看出, R1(X)是用来表征二值化后输入信息的损失:
| ${R_1}(X) = X - {\beta _1}{H_1}$ | (3) |
继续对残差进行二值量化, 就可以得到输入X的二阶二值近似:
| ${R_1}(X) \approx {\beta _2}{H_2}$ | (4) |
那么, 现在可以定义输入X的二阶残差近似:
| $X \approx {\beta _1}{H_1} + {\beta _2}{H_2}$ | (5) |
类似的, 我们可以定义出输入X的高阶残差, 以及相应的高阶残差量化:
| $X \approx \sum\nolimits_{i = 1}^K {{\beta _i}{H_i}} $ | (6) |
显然, 如果阶数越高, 输入的信息损失会越少, 但是计算量会越大. 我们所熟悉的XNOR-net算法其实用的是一阶残差近似, 因此会有很大的精度损失. 而HORQ高阶残差算法可以极大程度上保证网络的精度, 同时为了避免过于复杂的计算量, 我们一般采用二阶残差近似来进行实验.
这个方法有很大的发展前景. 对于一般的深度学习网络, HORQ 方法能够在很大程度上加速深度网络的计算速度. 由于网络每一层的输入和权值都被二值化, 模型的前向传播时间得到大大降低, 同时存储模型所需的空间也得到大大压缩, 这就使得在资源受限的小运算平台(例如手机和笔记本)上运行大规模的深度网络模型成为可能. 另外, 高阶残差量化的方法能够使得网络精度得到保证, 使得网络不再会因为简单的二值化方法而造成精度的大幅下降.
2 “分阶段残差二值化”算法这一部分介绍基于高阶残差量化网络所提出的二值网络的“分阶段残差二值化”训练优化算法, 该算法分别对权重和输入的二值化过程分阶段进行处理, 从而提高了最终二值模型的精度. 简单来说, “分阶段”也是一种确定式二值化, 但是与之前确定权重二值化不同的是, 这一算法将解决BNN的训练精度问题, 分别对权重和输入的二值化过程分阶段进行处理, 从而提高最终二值模型的精度.
本文基于高阶残差量化网络的思路设计了二值网络的“分阶段残差二值化”算法, 该算法使用残差来弥补精度损失. 下面将分为两个部分进行介绍: 第一, “分阶段二值化”算法的实现; 第二, 基于高阶残差量化方法改进的“分阶段残差二值化”算法的实现.
2.1 “分阶段二值化”算法的实现 2.1.1 “分阶段二值化”算法的推导流程在确定权重二值化的基础上, 参考XNOR-net对输入数据的处理办法, 给二值化输入增加近似因子
通过图4的表示方式, 可以很容易发现分阶段对中间值进行二值化处理时, 需要求近似核的部分恰好是不同通道上对应的相同位置.

|
图 4 关于中间值矩阵的“分阶段二值化”示意图 |
对输入近似因子的推导过程如下所示:
| ${X^{\rm T}} * W \approx (\beta * {H^{\rm T}} * \alpha * \beta )$ | (7) |
| $\beta = (\frac{1}{n}\parallel X{\parallel _{{l_1}}})$ | (8) |
参与近似因子
需要特别注意, 使用“分阶段二值化” 算法处理中间值时与处理权重不一样的地方:
首先, 权重的近似因子
其次, 在
至此, 我们通过理论分析和数值推导已经得到了“分阶段二值化”算法, 算法具体过程总结如下:
1) 首先, 实现对权重的阶段二值化, 将模型在BWN结构中达到接近单精度浮点数据的模型准确率. 阶段二值化根据网络中设定的“二值化比例”ratio这一参数, 选取权重矩阵的前ratio行, 即总共n组通道权重中的前ratio进行二值化, n为该层神经网络输出的特征数.
2) 然后, 当权重二值化的比例达到100%, 并将其模型finetune到接近全精度模型的准确率后, 开始提高中间值的二值化比例. 关于二值化中间值的选取方式与权重类似, 按照中间值矩阵的列进行确定式选择. 恢复到特征图的形状, 则可以理解成从特征图的左上角开始, 以滑动窗口的方式向右、向下逐渐覆盖整个特征图.
3) 最后, 当中间值的二值化比例也达到100%后, 继续finetune直到模型的准确率不再提高.
2.2 “分阶段残差二值化”算法的实现在“分阶段二值化”算法的基础上, 本文基于高阶残差量化网络的思想, 来进一步改进这一针对BNN和XNOR-net的训练优化算法. 现有的XNOR-net算法在使用中间值的近似因子时, 可以将其看做是一种乘法近似, 即:
| ${X^{\rm T}} * W = \beta * ({H^{\rm T}} * W)$ | (9) |
在使用上述算法时, 我们对中间值近似因子
这里我们使用一种新的近似因子求解方法, 即:
| $\beta = X - H$ | (10) |
其中,
这样卷积的计算过程就由式(5)变为:
| ${X^{\rm T}} * W = ({H^{\rm T}} + \beta ) * W = {H^{\rm T}} * W + \beta * W$ | (11) |
这样一来, 残差因子
本文基于高阶残差量化的思想对“分阶段二值化”算法进行了改进, 提出了二值网络的“分阶段残差二值化”训练优化算法, 该算法分别对权重和输入的二值化过程“分阶段”进行处理, 从而提高了最终二值化网络模型的精度.
3 实验结果与分析本文的实验主要分为两个部分:
第一部分是本文的重点部分, 即对二值网络的训练过程进行优化, 使用本文所提出的二值网络“分阶段残差二值化”算法, 以期在实现深度模型实时运行和降低运行内存占用的同时, 提升二值化网络模型的训练精度, 并且达到更好的识别准确率, 继续保有深度模型的优势.
第二部分主要是验证XNOR-net以及随机量化网络在特殊层上(这里以DECONV层为例)的有效性, 并验证XNOR-net网络相较于原始的全精度网络在效率上的优势.
3.1 数据集及实验设置 3.1.1 数据集及评判标准本文实验所使用的是CITYSCAPES数据集. CITYSCAPES评测数据集是一个大规模数据集, 在2015年由奔驰公司推动发布, 是目前公认的自动驾驶领域内最具权威性和专业性的图像语义分割评测集之一. 其主要关注真实场景下的城区道路环境理解, 在任务难度更高, 并且更贴近于自动驾驶等热门需求.
CITYSCAPES评测集包含5000多张高质量的像素级标注街景图片, 其主要被应用在图像语义分割任务[15]中, 用于评估视觉算法在城区场景语义理解方面的性能. 这其中共包含50个城市不同情况下的街景, 以及30类物体标注. CITYSCAPES主要专注于像素级别的分割和识别, 虽然其图像相对于真实的驾驶场景来说较干净, 但像素级别的分割和识别却提出了更高的要求. CITYSCAPES使用标准的PASCAL VOC IoU(intersection-over-union)得分来评估预测结果与真实场景之间的匹配准确度, 每个像素点的预测结果都会直接影响到最终得分.
3.1.2 实验设置普通的神经网络层主要包括卷积层、全连层等, 一般的二值网络算法也都是在CONV层上进行研究, 而且大量实验证明二值深度学习框架在基本层上的计算是正确的. 为了进一步验证其他特殊层的实现没有问题, 本文将算法改进拓展到其他特殊神经网络层, 这里以DECONV层为例进行验证.
本文对一套利用到DECONV层的网络结构进行了复现, 并在CITYSCAPES数据集上进行了训练. 训练发现, 在除最后一层之外的其他CONV、DECONV层使用XNOR-net算法和随机量化算法实现的网络层, 能够使模型正常收敛, 初步证明了在特殊层中算法实现的正确性.
但是对于一些大型的分类网络或回归模型, 二值网络往往不能满足准确率的要求, 这就导致无法在实际生产中大规模使用二值网络, 也就无法真正发挥它速度快、空间小、能耗低的性能优势. 为了更好地保持深度模型在二值网络中的训练结果, 本文结合随机量化算法和XNOR-net进一步提出了“分阶段残差二值化”这一训练优化算法, 并通过实验验证了该算法能在不增加使用复杂度的条件下, 实现二值网络模型在精度上的有效提升.
3.2 实验结果 3.2.1 “分阶段残差二值化”算法在测试集上的性能为了验证本文设计的“分阶段残差二值化”算法的有效性, 本节将对采用了“分阶段残差二值化”算法、高阶残差量化算法、随机量化算法训练所得模型的分割mask效果图与全精度模型的分割mask效果图进行对比, 由于采用了随机量化算法的网络在训练集上不能收敛, 这里将不考虑基于该算法模型的分割结果. 最终的分割mask效果如图5所示.
通过上述实验可以看出: (1)高阶残差量化模型比本文设计实现的分阶段残差二值化模型的分割效果要差, 不能清晰地分割图片中的物体; (2) “分阶段残差二值化”模型的分割效果接近原始全精度模型的分割效果, 皆能有效地分割图片中的物体.

|
图 5 高阶残差量化、“分阶段残差二值化”、原始全精度分割模型效果对比 |
3.2.2 “分阶段残差二值化”算法在训练集上的性能
为了验证“分阶段残差二值化”算法的可行性与高效性, 本节将对“分阶段残差二值化”算法的训练结果进行分析, 并与高阶残差量化网络、随机量化网络、原始全精度网络的训练结果进行对比. 对于“分阶段残差二值化”网络的训练, 首先对中间值进行阶段二值化, 等模型finetune完再对权重进行分阶段二值化.
实验中分别设置了不同的中间值二值化比例和权重二值化比例, 并记录了相对应的训练轮数. 实验结果如图6所示.
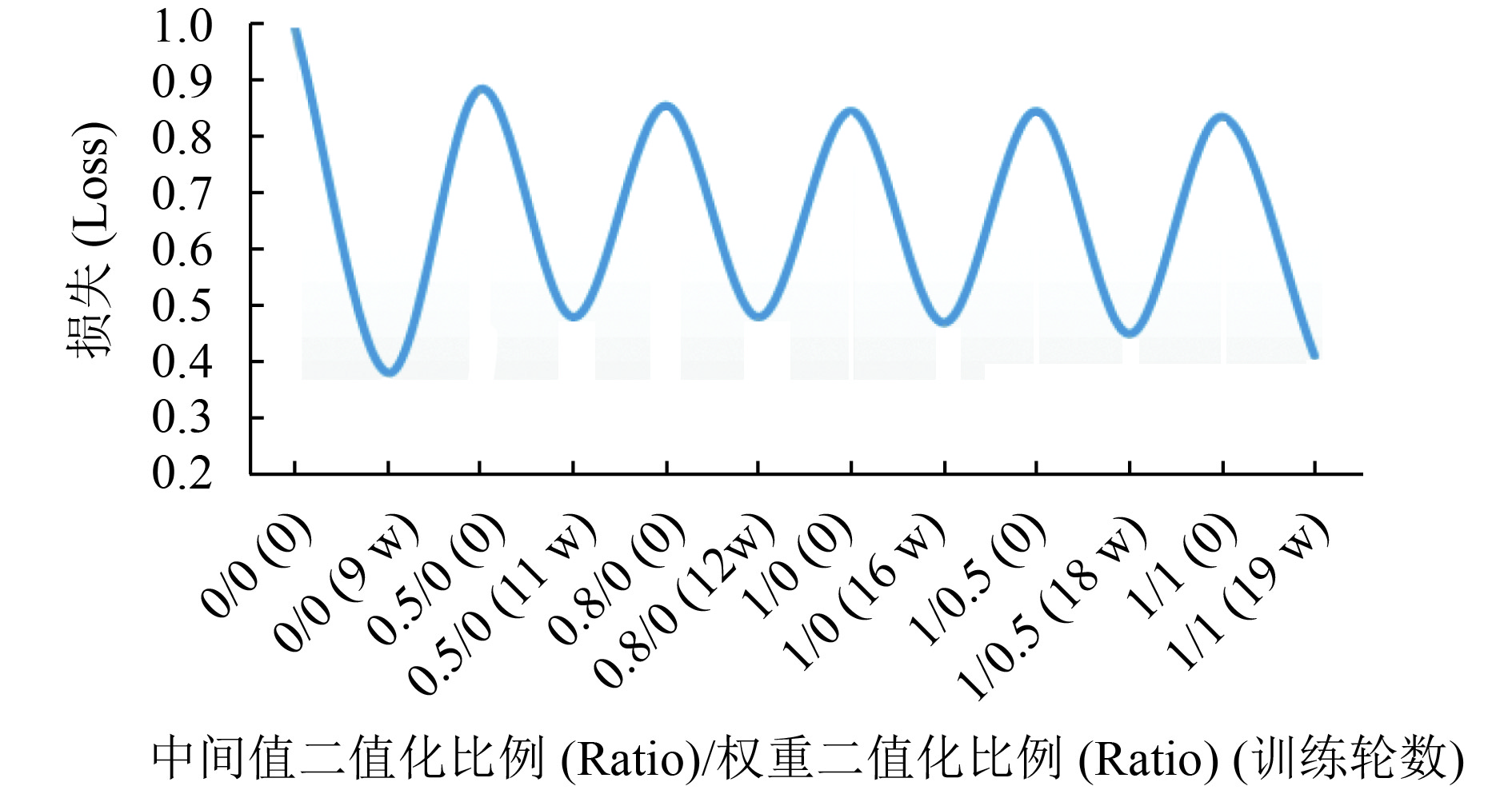
|
图 6 分阶段残差二值化训练结果 |
通过上面的训练结果我们可以发现该算法带来的最大好处在于能够使二值网络训练的模型更好地逼近原始全精度模型的效果.
除此之外, 我们还在训练集上对比了“分阶段残差二值化”模型与原始全精度模型、高阶残差量化模型、随机量化模型在accuracy和loss两大指标上的差异, 结果如表1所示.
| 表 1 “分阶段残差二值化”模型与原始全精度模型、高阶残差量化模型、随机量化模型的量化指标对比 |
综合上述实验可以看出: (1)随机量化模型难以收敛; (2)“分阶段残差二值化”模型比高阶残差量化模型收敛得快, 而且训练所得到的accuracy比高阶残差量化模型要高; (3)无论在accuracy还是在loss上, “分阶段残差二值化”模型都与单精度浮点模型十分接近.
3.2.3 “分阶段残差二值化”算法在特殊层上的实现为了进一步验证“分阶段残差二值化”算法不仅能在神经网络的基本层(例如: 卷积层, 全连层等)上实现, 也能在其他特殊层上正常实现, 本小节将以DECONV层为例来验证“分阶段残差二值化”算法的通用性.
我们对前文提到的基于随机量化算法以及基于高阶残差量化算法的网络进行了实验, 通过观察实验结果不难发现, 最后一层的DECONV在使用了这两种算法的网络上不能有效收敛, 而采用了“分阶段残差二值化”的训练方式后, 整个网络的收敛结果明显提升.
我们对比了几种结构下只针对最后一层特殊层, 即DECONV层进行二值化(计算量占比达到40%)的实验结果, 如表2所示.
| 表 2 “分阶段残差二值化”算法的实验 |
综合上述实验可以看出: (1)基于随机量化算法和高阶残差量化算法的网络不能用于特殊层; (2)基于“分阶段残差二值化”算法的网络在特殊层上能正常收敛, 因此该算法能适用于特殊层.
1) 在DECONV层上的实现
首先, 我们对一套利用到DECONV层的网络结构进行了复现, 并且在CITYSCAPES数据集上进行了训练. 通过训练, 我们发现: 在除最后一层之外的其他CONV层、DECONV层使用“分阶段残差二值化”算法实现的网络层能够使模型正常收敛, 初步证明了在特殊层中算法实现的正确性, 实验结果如表3所示.
| 表 3 对DECONV使用“分阶段残差二值化”训练的效果 |
通过分析表3中的数据, 我们可以发现, 大部分网络层(包括特殊层)采用了“分阶段残差二值化”算法的模型后, 可以达到与全精度网络训练得到的模型相近的精度效果.
2) 速度对比
其次, 除了对识别精度的验证外, 我们更关注的是二值模型的运行速度, 关心它能否实现CPU环境下的实时运行. 因此我们在CPU硬件环境下, 对不同规模、不同种类的神经网络进行了速度方面的对比, 统计了二值模型相比于全精度权重模型的加速比. 实验结果如表4所示.
表4中, Full代表Full precision, staged代表“staged residual binarization”. 结合表中统计的实验结果, 分析可得: “分阶段残差二值化”所统计的时间不仅有异或位运算和popcount函数所构成的二值计算部分, 还包括对权重的按位压缩处理, 以及对中间值按位压缩改造过的im2col处理. 而全精度的运行时间则只是统计了乘法运算部分, 原始的im2col处理并没有包含在内. 如果通过caffe本身的time函数计算时间以及在函数外部打印时间两种方式去统计神经网络层的运行时间, 得到的结果反映出“分阶段残差二值化” 能够实现5倍左右的提速.
| 表 4 原始全精度模型与“分阶段残差二值化”模型在不同结构上运行的用时对比(单位: ms) |
综上所述, 本文基于高阶残差量化算法所设计的“分阶段残差二值化”算法, 能够有效利用全精度的预训练模型, 降低了二值网络的训练难度, 使二值网络最终收敛到与原始全精度深度模型接近的准确率水平. 在语义分割等复杂任务上进行的实验结果表明, 本文所提出的“分阶段残差二值化”算法对于二值网络的优化训练、提升模型准确率有着非常明显的作用, 而且不增加测试计算量, 从而保持了二值网络速度快、空间小、能耗低的优势.
4 结论本文主要工作有两点: (1) 对CNN中二值网络的实现及训练技巧进行优化总结, 构建了“二值深度学习框架”; (2) 基于高阶残差量化网络提出了一种全新的“二值网络的分阶段残差二值化算法”. 前一项工作包含对二值网络结构的理论研究及优化调整; 后者所提出的算法能够显著提升二值网络训练效果, 得到接近全精度神经网络的识别准确率, 具有较高的现实意义和使用价值.
| [1] |
Hou L, Yao QM, Kwok JT. Loss-aware binarization of deep networks. arXiv: 1611.01600, 2016.
|
| [2] |
Coates A, Huval B, Wang T, et al. Deep learning with COTS HPC systems. Proceedings of the 30th International Conference on International Conference on Machine Learning. Atlanta, GA, USA. 2013. III-1337–III-1345.
|
| [3] |
Vanhoucke V, Mao MZ. Improving the speed of neural networks on CPUs. Proceedings of Deep Learning and Unsupervised Feature Learning (NIPS Workshop 2011). Grarada, Spain. 2011. 1–4.
|
| [4] |
Gong YC, Liu L, Yang M, et al. Compressing deep convolutional networks using vector quantization. arXiv: 1412.6115, 2014.
|
| [5] |
Romero A, Ballas N, Kahou SE, et al. FitNets: Hints for thin deep nets. arXiv: 1412.6550, 2014.
|
| [6] |
Farabet C, LeCun Y, Kavukcuoglu K, et al. Large-scale FPGA-based convolutional networks. Bekkerman R, Bilenko M, Langford J. Machine Learning on Very Large Data Sets. Cambridge: Cambridge University Press, 2011.
|
| [7] |
Pham PH, Jelaca D, Farabet C, et al. NeuFlow: Dataflow vision processing system-on-a-chip. Proceedings of the 2012 IEEE 55th International Midwest Symposium on Circuits and Systems. Boise, ID, USA. 2012. 1044–1047.
|
| [8] |
Chen TS, Du ZD, Sun NH, et al. DianNao: A small-footprint high-throughput accelerator for ubiquitous machine-learning. ACM SIGPLAN Notices, 2014, 49(4): 269-284. |
| [9] |
Esser SK, Appuswamy R, Merolla PA, et al. Backpropagation for energy-efficient neuromorphic computing. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada. 2015. 1117–1125.
|
| [10] |
Kamiya R, Yamashita T, Ambai M, et al. Binary-decomposed DCNN for accelerating computation and compressing model without retraining. Proceedings of 2017 IEEE International Conference on Computer Vision Workshops. Venice, Italy. 2017. 1095–1102.
|
| [11] |
Umuroglu Y, Fraser NJ, Gambardella G, et al. FINN: A framework for fast, scalable binarized neural network inference. arXiv: 1612.07119, 2016.
|
| [12] |
Courbariaux M, Bengio Y, David JP. Binaryconnect: Training deep neural networks with binary weights during propagations. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada. 2015. 3123–3131.
|
| [13] |
Courbariaux M, Bengio Y, David JP. Training deep neural networks with low precision multiplications. arXiv:1412.7024, 2015.
|
| [14] |
Rastegari M, Ordonez V, Redmon J, et al. XNOR-Net: Imagenet classification using binary convolutional neural networks. Proceedings of the 14th European Conference on Computer Vision. Annsterdam, The Netherland. 2016. 525–542.
|
| [15] |
Paszke A, Chaurasia A, Kim S, et al. ENet: A deep neural network architecture for real-time semantic segmentation. arXiv: 1606.02147, 2016.
|
 2019, Vol. 28
2019, Vol. 28


