2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 沈阳市环境检测中心站, 沈阳 110000;
4. 沈阳市第二十七中学, 沈阳 110011
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Shenyang Environmental Monitoring Center Station, Shenyang 110000, China;
4. Shenyang Twenty-Seventh Middle School, Shenyang 110011, China
视频或者图像在传输过程中, 可能出现随机性的误码、突发性的误码、传输中的丢包、时延过大或不均匀、定时抖动、传输包倒序等等问题, 导致接收端解码出的图像质量严重下降. 例如视频在网络传输中由于网络拥堵导致视频编码后某一帧的宏块包丢失造成解码端产生误码, 解码输出的视频帧出现类似马赛克的色块, 还会影响到与之相关的后续数据的解码, 造成误码扩散, 使误码环境下解码生成的画面连续出现色斑, 造成视频质量严重下降. 于是, 建立合适的模型利用退化系统的先验知识来降低或者消除观察图像中的失真, 得到一个高质量的图像以便于观察或者进一步处理图像复原过程显得尤为重要. 目前图像重建技术主要分为两类: 一是基于插值的重建方法, 利用多张图像的丰富信息, 图像间的相同或相异信息以及图像的先验知识进行重建, 例如邻域像素重复技术和双三次图像插值技术等, 修复效果不佳. 二是基于学习的图像重建方法, 目前用于单幅图像重建的最先进的方法大多是基于样本学习的. 这些方法主要利用相同图像的内部相似性, 或外部样本学习映射函数. 基于样本的外部方法通常提供有大量丰富样本, 但是受到有效紧凑建模数据困难的挑战.
近年来, 基于深度学习的方法得到了广泛的关注, 在如目标分类、人脸识别、文本识别[1,2]等众多计算机视觉问题中取得了优于传统方法的显著效果. 本文对深度学习在图像恢复重建问题中的应用进行探索, 设计了用于图像重建的卷积神经网络结构, 利用重建损失和对抗损失优化模型参数, 增强重建图像的纹理细节信息, 减少重建图像与真实图像在结构误差. 用海量图像构造训练样本, 对设计的深度卷积神经网络进行训练以实现图像的重建, 在三组包含大量弱纹理区域的测试图像序列中取得了优于基于插值方法的效果.
1 卷积神经网络模型总体设计本文提出的神经网络模型主要分为三个模块: 对图像进行卷积操作提取特征、对提取的特征进行反卷积重建图像, 利用重建的图像与原图像的重建损失和对抗损失优化模型参数.
神经网络模型的设计总框架如图1所示.

|
图 1 神经网络结构示意图 |
1.1 卷积提取图像特征
本文卷积模块基于标准的卷积神经网络进行设计, 由卷积层和激活函数层交替重复排列. 卷积层中本文将卷积核尺寸、步幅和内边距填充依次设为4, 2, 1. 激活函数层则采用线性单元激活函数. 如图1所示, 输入图片的尺寸为128×128, 数据经过64个4×4×3的卷积核和激活函数进行处理得到64个64×64的特征图, 然后进入下一层特征提取, 其中卷积核为64个4×4×64, 得到64个32×32的特征图, 同样依次处理,最后得到包含4000个元素的特征向量.
1.2 反卷积重建图像为使整个神经网络的输出和输入保持同一空间分辨率, 本文卷积神经网络模型中采用反卷积进行图像重建. 反卷积其实是对卷积的逆向操作, 也就是通过将卷积的输出信号, 经过反卷积可以还原卷积的输入信号. 如图1所示反卷积层由一系列具有学习滤波器的六层向上卷积层[3–5], 每一层都有一个反卷积核和线性单元激活函数交替组成. 反卷积就是一个能输出高分辨率图像的卷积函数, 可以理解为对输入进行卷积计算后再做上采样的处理. 如图1所示由前六层卷积提取的特征特征向量经过一系列的向上卷积层卷积、池化、激活处理得到高分辨率图像, 直到得到与输入图像尺寸相近的图像为止.
1.3 重建图像损失为了计算重建图像的损失, 损失函数考虑了重建损失和对抗损失. 重建损失则采用基于原图像和重建图像矩阵之间的2-范数作为标准. 在实验中发现, 如果只考虑重建损失, 会导致训练得到的神经网络重建出的图像丢失过多图像结构等轮廓细节信息. 所以本文损失函数引入对抗损失, 利用对抗神经网络[6]测度重建出的图像与真值图像之间的结构信息损失. 模型总的损失设计为重建损失和对抗损失的加权和.
2 神经网络模型各个模块的原理算法的整个计算过程: 输入图像→卷积→激活→图像特征→反卷积→激活→重建的图像. 可视化网络结构如图2.
2.1 特征提取本文的特征提取部分采用6层卷积网络结构[7], 并采用多个卷积核对图像进行卷积提取特征, 得到图像特征向量. 图像的卷积操作, 可以写成矩阵形式.

|
图 2 可视化神经网络模型 |
图3表示对图像做卷积, 一个典型的4×4卷积核, 其输出结果中的每个元素都与输入图片一个4×4小方块相连, 也就是说输出层的这个像素值只是通过输入层的这个小方块中的像素值计算而来. 整个输出层就相当于将原矩阵按照顺序将各区域元素与权重W矩阵做内积, W矩阵为:
| $W = \frac{1}{9}\left( {\begin{array}{*{20}{c}} 1&1&1&1 \\ 1&1&1&1 \\ 1&1&1&1 \\ 1&1&1&1 \end{array}} \right)$ | (1) |

|
图 3 图像卷积示意图 |
式(1)矩阵中的权重系数1表示权重矩阵的初始值, 卷积神经网络每次迭代计算都更新权重矩阵中的权重系数. 卷积核对图像进行操作, 相当于对图像进行了低通滤波. 因此卷积核核也被称为滤波器, 整个操作过程称为卷积. 对二维图像的卷积操作可以看成对图像进行滤波处理, 比如常见的高斯滤波、拉普拉斯滤波(算子)等. 如果要识别图像中的某种特征, 这个滤波器要对这种特征有很高的输出, 对其他形状则输出很低, 这也就像是神经元的激活.
在训练卷积神经网络的时, 使用一系列不同的滤波器提取图片不同的特征, 训练神经网络中不断迭代更新滤波器权重系数、偏置系数等参数. 如图2所示, 特征提取的第一层采用64个4×4的滤波器, 输出层得到64个特征图, 然后对特征图做池化激活处理, 第二层用128个滤波器处理这64个特征图得到128个特征图, 后面的卷积层依次处理, 最后得到输入图像的特征向量.
2.2 图像重建图像重建部分主要对卷积模块生成的特征向量进行反卷积处理. 反卷积层由反卷积核和线性单元激活函数交替组成, 反卷积能输出高分辨率图像, 可以理解为对输入进行卷积计算后再做上采样的处理, 直到输出图像大小和真值图像大小相同.
在神经网络中, 线性单元激活函数是用于保证每层输出的激活值都是正数, 因此对于反向过程, 同样需要保证每层的特征图为正值, 也就是说这个反激活过程和激活过程没有什么差别, 直接采用线性单元激活函数. 如图2可视化神经网络模型所示, 图像重建部分每一层由向上卷积核和池化函数、激活函数组成, 第一层将特征提取部分输出的特征向量进行向上卷积、池化、激活处理得到512个4×4的特征图, 然后经过下一层处理得到512个8×8的特征图, 依次处理重建出原图像缺失部分的局部图像, 然后将原图像与重建的局部图像[8]融合成一张128×128的目标图像.
2.3 损失函数为了测度重建图像与真值图像在纹理细节和结构上的差距, 使重建图像的纹理细节和结构信息损失最小化, 本文神经网络模型的损失函数采用了重建损失和对抗损失的加权和. 重建损失使用2-范数测度重建图像和真值图像之间的距离, 公式为:
| ${l_\gamma} = d\left( {G(Z) - Z} \right) = {\left\| {G(Z) - Z} \right\|^2}$ | (2) |
式(2)中, Z表示输入原图像, G(Z)表示重建图像,
引入生成对抗神经网络得到重建图像的对抗损失, 对抗神经网络如图4所示, 主要由卷积神经网络G和卷积神经网络D组成, 卷积神经网络G表示生成模型, D表示判别模型, 其中G: Z→X将来自噪声分布Z的样本映射到数据分布X. 学习过程是双人游戏, 其中判别器D同时考虑G和真实样本的预测, 并试图区分它们, 而G试图通过产生尽可能表现为“真实”的样本来混淆D. 判别器D的目标是指示输入是真实样本还是预测样本的逻辑可能性.
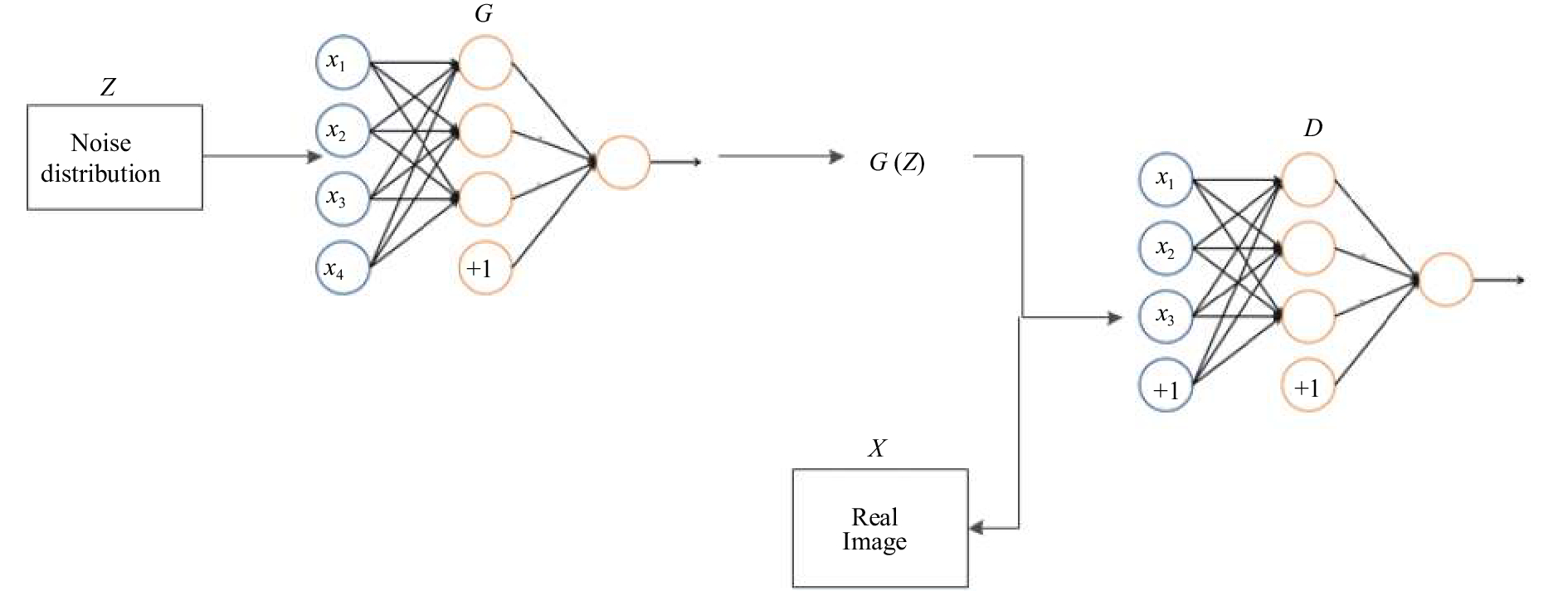
|
图 4 对抗神经网络示意图 |
图4中生成模型G重建出的图像为G(Z), 图像X表示与残缺图像Z对应的原完整图像, 在判别模型D中, 重建图像G(Z)和原完整图像X为输入图像, D的输出则是判断图像G(Z)与图像X是同一幅图像的逻辑可能性, 是一个常量. 判别图像对于G来说, 重建出的图像要不断的欺骗判别D, 那么也就是:
| $\max \log_{10} (D(G(z)))$ | (3) |
对于D来说, 要不断的学习防止被G欺骗, 也就是:
| ${l_a} = \mathop {\max }\limits_D (\log_{10} (D(x)) + \log_{10} (1 - D(G(z))))$ | (4) |
式(4)中,
本文中对抗损失则为生成对抗神经网络的整个输出值, 即生成模型G输出的重建图像为真实图像的逻辑可能性.
重建损失主要反映了新生成的图像内容纹理细节与真值图像的距离, 对抗损失使用对抗神经网络模型测度重建图像和真值图像在结构上的差异. 为了使重建的图像更加逼近真实图像. 本文中损失函数定义为:
| $\ell {\rm{ = }}{\lambda _\gamma}{l_\gamma} + {\lambda _\alpha}{l_\alpha}$ | (5) |
式(5)中,
本文使用Google发布的Open Image图片数据集训练上文设计的卷积神经网络模型, 该数据集包含大概900万张图片, 这些图像横跨6000多个类别, 具有很高的分辨率. 实验证明采用高分辨率图像数据集比采用较低分辨率图像数据集, 使模型有更强的鲁棒性. 本文随机从Open Image数据集中选取100 000张图像作为训练集, 并进行尺寸为
本文的卷积神经网络模型的训练分为两个阶段:首先模型先经过一个六层的卷积神经网络提取特征, 输出一个包含4000个元素的特征向量; 其次, 将特征向量输入反卷积重建神经网络, 重建生成缺失的图像块, 将生成的图像块与原图像拼接成完整图像. 在反复的训练中发现去除卷积神经网络中的池化层, 激活函数使用线性单元函数, 重建的图像能保持较好的局部纹理细节. 在神经网络模型在训练过程中初始学习率设为0.001, batch设置为50, 不断训练模型, 优化权重参数, 直到损失函数值稳定在区间[0.005+0.0005].
本文算法评估数据集使用超分辨率研究领域通用的测试数据集合Set5[9]、Set14[9]、BSD100[10], 评测标准为PSNR(峰值信噪比), 单位是dB, PSNR是最普遍, 最广泛使用的评鉴画质的客观量测法, 其值越大就代表失真越少. 公式为:
| $PSNR = 10 \times {\log _{10}}\left( {\frac{{{{\left( {{2^n} - 1} \right)}^2}}}{{MSE}}} \right)$ | (6) |
其中, MSE是原图像与重建图像之间均方误差.
实验中本文算法与SRCNN[9]算法、Bicubic算法、ESRCNN算法在评测数据集上进行对比. 本文算法在Set5、Set14、BSD100数据集上PSNR值(表1)与另外3个算法相近, ESRCNN算法为SRCNN算法的改进型增加了卷积层, Ours(
| 表 1 四种算法实验结果(PSNR) |
图5是四种算法的图像重建实验结果, 从左到右依次为SRCNN算法、Bicubic算法、ESRCNN算法和本算法重建生成的图像, Bicubc算法重建的第一幅图像生成的图像块在结构上有错位, ESRCNN算法重建的第三幅图像生成的图像块在结构上比原图像多出一部分. 从图5中可以看出本文提出的算法基重建生成的图像在结构上与原图像中其他部分融合的很好, 视觉上没有明显的突兀感. 另外本文提出的重建算法生成的图像在纹理细节上比较清晰, 图中重建出的树和背景图像层次分明. 直观的从视觉上分析结果和表1数据反映结果一致. 总的来说, 本文给出的神经网络模型重建的图像失真度较小, 较好地重建了图像的纹理和结构信息.
4 结论与展望本文提出了一种基于图像背景预测模糊区域内容的无监督图像重建神经网络模型, 引入了对抗神经网络模型计算重建图像的对抗损失, 重建损失主要反映了新生成的图像内容纹理细节与真值图像的距离, 对抗损失使用对抗神经网络模型测度重建图像和真值图像在结构上的差异. 最后模型在三个不同的数据集下进行了实验, 并且证明该算法模型能够较好地重建图像. 下一步工作, 考虑将图像重建应用到视频单帧图像重建, 视频相邻帧之间存在着大量的互补冗余信息, 重建视频帧可以同时利用帧之间的时序相性和单帧图像块之间的空间相关性来改进模型使之可以处理视频信息, 提高视频质量, 尝试结合视频帧的时序、空域相关性等特征信息共同参与模型的训练和学习.

|
图 5 四种算法的图像重建实验结果 |
| [1] |
Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality. Advances in Neural Information Processing Systems 26. 2013. 2–3.
|
| [2] |
LeCun Y, Boser B, Denker JS, et al. Backpropagation applied to handwritten zip code recognition. Neural Computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541 |
| [3] |
Dosovitskiy A, Springenberg JT, Brox T. Learning to generate chairs with convolutional neural networks. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA. IEEE. 2015. [doi: 10.1109/CVPR.2015.7298761]
|
| [4] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA. IEEE. 2015.
|
| [5] |
Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. In: Fleet D, Pajdla T, Schiele B, et al., eds. Computer Vision–ECCV 2014. Lecture Notes in Computer Science, vol 8693. Springer, Cham. 2014. 818–833. [doi: 10.1007/978-3-319-10590-1_53]
|
| [6] |
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. arXiv, 2014: 1406.2661.
|
| [7] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [8] |
Hays J, Efros AA. Scene completion using millions of photographs. ACM SIGGRAPH, 2007. DOI:10.1145/1239451.1239455 |
| [9] |
Dong C, Loy CC, He KM, et a1. Learning a deep convolutional network for image super-resolution. In: Fleet D, Pajdla T, Schiele B, et al., eds. Computer Vision–ECCV 2014. Lecture Notes in Computer Science, vol 8692. Springer, Cham. 2014. 184–199. [doi: 10.1007/978-3-319-10593-2_13]
|
| [10] |
Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. Proceedings of the Eighth IEEE International Conference on Computer Vision. Vancouver, BC, Canada. 2001. 416–423. [doi: 10.1109/ICCV.2001.937655]
|
 2018, Vol. 27
2018, Vol. 27



