1 引言

单通道语音增强方法因其算法复杂度适中, 算法的实现对硬件需求不大, 而在很多领域受到广泛的应用. 在单通道话音增强算法中, 噪声估计是至关重要的一环. 在这一环节中, 主要任务就是对噪声功率谱进行准确的估计, 这样才能较好的抑制噪声, 同时保证较好的话音质量, 否则会产生过减或欠估计现象, 前者会导致话音失真, 影响语音可懂度, 后者则会导致的噪声残留, 影响听觉体验.

全球很多学者提出了多种噪声估计方法. 在这些噪声估计算法里面, 最具代表性的有Martin在2001年提出的MS最小统计量噪声估计算法^[1], 该算法在固定的搜索窗内搜索含噪语音功率谱最小值. 在2002年, Israel Cohen提出了MCRA (Minima Controlled Recursive Averaging)最小递归控制平均算法^[2], 该算法通过将当前帧带噪话音子频带局部功率谱与搜索窗内对应的最小功率谱比较, 以此确定该频带是否含有话音成分. MCRA算法在话音噪声谱增加缓慢(噪声谱增加小于2 dB/s)的情况下^[3], 有良好的噪声估计能力, 能够通过递归平均法准确估计噪声值. 但该算法采用了固定搜索窗长来更新最小功率谱值, 当话音出现噪声谱陡增的情况时, 噪声估计会出现延迟. 延迟时间在L到2L帧之间, 其中L为一个最小噪声估计窗长, 为了保证话音无失真, L时间长度通常选为800 ms~1500 ms.

为解决噪声估计延迟, 广大学者也做了一些研究. 2005年, Loizou提出在MCRA噪声估计算法的基础上引入连续平滑噪声更新^[4], 改进后的算法有效的缩短了噪声估计延迟, 但是该算法在低信噪比下存在噪声过估计情况, 导致话音失真. 2009年, 贺慧芳, 马建芳在MCRA算法的基础上提出了一种基于语音帧检测的算法^[5]来加快噪声估计速度, 该算法在较高信噪比条件下可以有效的缩短噪声估计延迟, 在低信噪比下对噪声估计延迟的改进有限. 2015年, 熊晶, 王旭贞等人在MCRA算法的基础上提出了一种双向噪声估计算法^[6,7], 该算法可以较好的解决噪声估计延迟以及过估计问题, 但是实现该算法需要在缓存一段话音数据, 不适合实时性要求较高的场合.

本文在MCRA噪声估计算法的基础上, 引入一种利用最大对数似然比结合能零比的VAD辅助算法, 通过该辅助算法, 可以动态的选择大小噪声搜索估计窗中的最小功率谱值进行后续计算, 从而得到一种变窗长搜索的改进型噪声估计算法. 本文所提的改进算法能有效缩短噪声估计延迟, 也能在低信噪比环境下运行, 并且不需要缓存数据, 可以用于实时性要求较高的场合.

2 基于变窗长的MCRA改进算法

本节先介绍MCRA算法^[2]的基本原理, 然后介绍本文提出的双参数双门限VAD算法以及双窗并行搜索, 最后讲述本文算法如何进行噪声估计更新.

2.1 MCRA算法基本原理

当前带噪话音帧的功率谱为 ${\rm{|}}Y(k,l{\rm{)}}{{\rm{|}}^2}$ , 式中 $ k $ 表示子带数, $ l $ 表示帧数, 后文中 $ k $ 和 $ l $ 含义同此处相同. 根据文献[2], 先对当前帧功率谱做频域上的平滑:

${S_f}(k,l) = \sum\limits_{i = - N}^N {w(i)} |Y(k,l){|^2}$

(1)

其中, $w(i)$ 为一个长 $2N + 1$ 的窗函数, 文中算法取 $N = 1$ .

然后对当前帧功率谱做时域上的平滑:

$S(k,l) = {\alpha _s}S(k,l - 1) + (1 - {\alpha _s}){S_f}(k,l)$

(2)

其中, ${\alpha _s}$ 为一个经验值, 文中算法 ${\alpha _s}$ 为0.8 .

再按照如下方式更新 ${S_{\min }}(k,l)$ 和 ${S_{{\rm{tmp}}}}(k,l)$ .

当 $ l $ 不能被 $ L $ ( $ L $ 为定窗长)整除时:

$\left\{ {\begin{aligned} & {{S_{\min }}(k,l) = \min (S(k,l),{S_{\min }}(k,l - 1))} \\ & {{S_{\rm{tmp}}}(k,l) = \min (S(k,l),{S_{\rm {tmp}}}(k,l - 1))} \end{aligned}} \right.$

(3)

当 $ l $ 能被 $ L $ 整除时:

$\left\{ {\begin{aligned} & {{S_{\min }}(k,l) = \min ({S_{\rm {tmp}}}(k,l - 1),S(k,l))} \\ & {{S_{\rm {tmp}}}(k,l) = S(k,l)} \end{aligned}} \right.$

(4)

${S_{\min }}(k,l)$ 表示搜索窗内的最小功率谱值, ${S_{{\rm{tmp}}}}(k,l)$ 用来缓存最小功率谱值.

接着求得当前帧平滑功率谱 $S(k,l)$ 及最小功率谱值 ${S_{\min }}(k,l)$ 的比值 ${S_{{r}}}(k,l)$ :

${S_r}(k,l) = \frac{{S(k,l)}}{{{S_{\min }}(k,l)}}$

(5)

如果 ${S_{{r}}}(k,l)$ 大于经验值 ${\rm{sigma}}$ (本文算法 ${\rm{sigma = }}5$ ), 则带噪话音子带话音存在标志 $I(k,l)$ 置1, 否则 $I(k,l)$ 置0, 并更新子带语音存在概率:

$p(k,l) = {\alpha _p}p(k,l - 1) + (1 - {\alpha _p})I(k,l)$

(6)

式中, ${\alpha _{{p}}}$ 为一个经验值, 本文算法中 ${\alpha _{{p}}}$ 为0.9.

最后更新噪声估计值:

$\begin{array}{l}{\lambda _d}(k,l + 1) = {\lambda _d}(k,l)p(k,l) + (1 - p(k,l))({\alpha _d}{\lambda _d}(k,l) \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+ (1 - {\alpha _d})|Y(k,l){|^2})\end{array}$

(7)

2.2 双参数双门限VAD

(1) 基于能零比的VAD

在文献[8]中, Maragos提出了一种基于短时能零比的VAD算法, 即短时平均过零率与短时能量相结合的VAD算法, 该算法对噪声谱变化不敏感, 即噪声谱的陡增不会影响算法性能, 且能较好的区分浊音和非浊音, 但在低信噪比下对清音和噪声的区分效果不佳.

短时平均过零率表示一帧语音中信号时域波形穿越横轴的次数. 对于离散的信号, 如果相邻的取样值发生符号改变, 则称为过零. 短时平均过零率就是样本数值改变符号的次数.

高频信号意味着较高的平均过零率, 低频意味着较低的平均过零率. 通常情况下, 话音中出现浊音时, 过零率较低, 而出现清音以及白噪声、超短波噪声时, 过零率较高.

过零率可以通过下面的公式求得:

$Zcr(l) = \sum\limits_{n = 0}^{N - 1} {|{\rm{sgn}}[{y_l}(n)] - {\rm{sgn}}[{y_l}(n - 1)]|} $

(8)

式中, $l$ 代表帧数, $n$ 表示数据点数, $sgn{\rm{[ ]}}$ 为符号函数, $Z{{cr}}(l)$ 为第 $l$ 帧的过零率, ${y_l}(n)$ 为输入带噪话音数据第 $l$ 帧第 $n$ 个数据点.

在话音中的有话区间能量要高于无话区间, 过零率则相反, 现在结合这两种方法, 即用能量值除以过零率的值, 可以更突出有话区间的数值, 而噪声区间的数值则更小. 第l帧的能量可以根据下面公式求得:

$Energy{\rm{(}}l{\rm{)}} = \sum\limits_{k = 0}^{N - 1} {y{\rm{(}}l,k{\rm{)}}} $

(9)

这里引入对数能量计算公式:

$Log\_Energy{\rm{(}}l) = {\rm {lo}}{{\rm g}_{10}}{\rm{(}}1 + Energy{\rm{(}}l{\rm{)}}/a{\rm{)}}$

(10)

用对数表达式可以缓和能量幅度剧烈变换, 参数 $a$ 是一个经验值, 适当的调整好参数 $a$ 的值, 将有利于噪声和清音的区分, 在本文中将参数 $a$ 设置为2.

最后能零比通过以下公式求出:

$E{{cr(}}l{{) = Energy(l)/(Zcr(}}l{{) + }}b{{)}}$

(11)

参数 $b$ 是为了防止 $Z{{cr}}(l)$ 为0时出现异常值现象, 在本文中参数 $b$ 设置为1.

(2) 基于最大对数似然比的VAD

在文献[9]中, J Chang等人提出了基于高斯统计模型与拉普拉斯统计模型的最大对数似然比, 在文献[10]中, 夏丙寅等人基于上述模型提出了一种最大对数似然比VAD算法, 可以较好的区分清音和噪声. 为了保护清音部分, 本文选择最大对数似然比作为VAD辅助算法中的另外一种参数.

对每一帧话音信号, 话音存在假设为 ${H_1}$ , 话音不存在假设为 ${H_0}$ , 基于高斯统计模型, 可以求得带噪话音信号傅里叶变换后每个频点所对应的似然度, 可以表示为:

$\begin{aligned}& \wedge (k,l) = \frac{{p(Y(k,l)|{H_1})}}{{p(Y(k,l)|{H_0})}} = \frac{1}{{\xi (k,l)}}\exp \left\{ {\frac{{\gamma (k,l)\xi (k,l)}}{{1 + \xi (k,l)}}} \right\}\end{aligned}$

(12)

$Y(k,l)$ 为第 $l$ 帧带噪话音信号的傅里叶变换的第 $k$ 个子带处的频谱系数. $p(Y(k,l)|{H_1})$ 是假设话音存在情况下的条件概率, $p(Y(k,l)|{H_0})$ 是假设话音不存在情况下的条件概率. $\xi (k,l)$ 和 $\gamma (k,l)$ 分别为第 $l$ 帧话音信号的第 $k$ 个频点的的先验性噪比和后验信噪比. 两种信噪比分别可由DD判决法则^[11]得到, 分别表示为以下公式:

$\xi (k,l) = \frac{{{\lambda _x}(k,l)}}{{{\lambda _d}(k,l)}}$

(13)

$\gamma (k,l) = \frac{{|Y(k,l){|^2}}}{{{\lambda _d}(k,l)}}$

(14)

式(6)和式(7)中的 ${\lambda _d}(k,l)$ 表示噪声谱估计值.

基于对数似然比LLR的判决规则可得:

$LLR(l) = \log \wedge (l) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\log \wedge (k,l)} $

(15)

本文中将两种VAD算法结合起来, 利用能零比VAD对噪声功率谱变化不敏感, 以及最大对数似然比VAD能在低信噪比情况下较好的区分清音和噪声的特点, 提出一种双门限双参数的VAD算法, 并将其作为MCRA噪声估计算法的辅助算法.

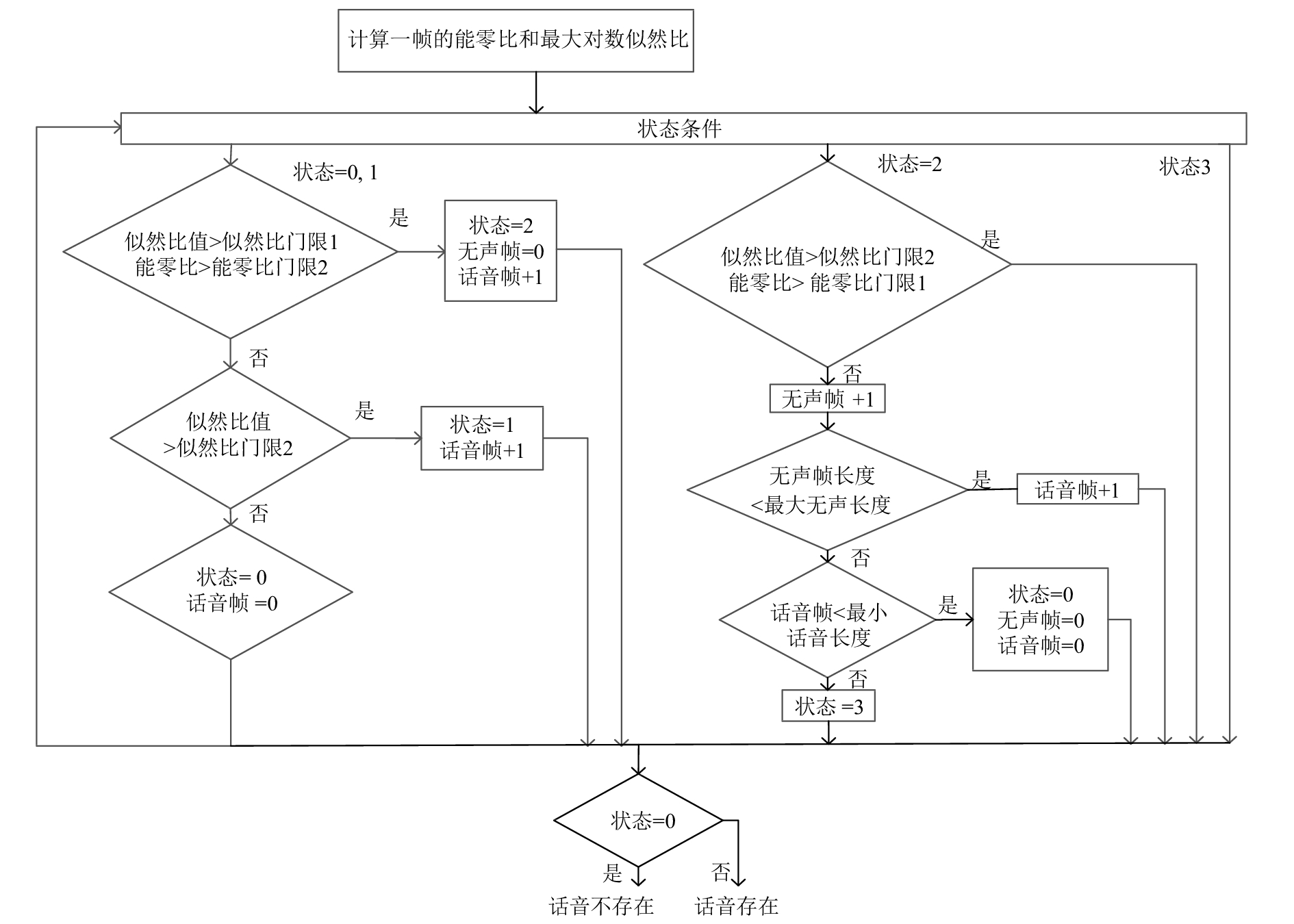
上述双参数双门限的VAD, 即以最大对数似然比以及能零比作为参数, 采用二级门限, 通过判决流程得到一个话音存在标记值. 具体的流程如图1所示.

状态0为“非话音段”、状态1位“疑似话音段”, 状态2为“话音段”, 状态3为“结束段”. 为方便描述, 此处用 $Ecr(l)$ 表示第 $l$ 帧的短时能零比值, 用 $LLR(l)$ 表示第 $l$ 帧的对数似然比值, $E{{cr}}1$ 、 $E{{cr}}2$ 分别表示二级能零比门限, $LLR1$ 、 $LLR2$ 分别表示二级对数似然比门限. $LLR1$ 取3, $LLR2$ 取0.4, $E{{cr}}1$ 取值为前五帧无话段的平均能零比值的1.3倍, $E{{cr}}2$ 取值为前五帧无话段的平均能零比值的1.7倍.

从状态0开始执行VAD算法. 如果当前状态为0或者1, 且 $Ecr(l)$ 大于 $E{{cr}}2$ 且 $LLR(l)$ 大于 $LLR1$ , 就把该帧话音标记为状态2, 并将无声帧计数器置0, 话音帧计数器加1. 若不满足该门限要求, 但 $LLR(l)$ 大于 $LLR2$ , 则把该帧话音标记为状态1, 话音帧计数器加1. 如果上述两级判决都不满足则把该帧话音标记为状态0.

如果当前状态为2, ${{Ecr(l)}}$ 大于 $E{{cr}}1$ 且 $LLR(l)$ 大于 $LLR2$ , 则维持当前状态. 不满足上述要求, 无声帧计数器加1. 若此时无声帧计数器的数值小于最长无声长度, 则认为当前帧依旧处于话音段, 话音帧计数器加1. 若无声帧计数器的数值大于最长无声长度, 且话音帧计数器的值小于最小话音长度, 则将该帧标记为状态0, 话音帧计数器和无声帧计数器置0, 否则将当前帧标记为状态3.

最终根据话音帧所处的状态做一个存在标记, 当状态为0时, 把当前帧标记为“语音不存在”, 其他状态则把当前帧标记为“语音存在”.

2.3 双窗法并行搜索

原MCRA算法, 噪声搜索窗选用固定的窗长, 而本文算法选用两个大小不同的窗^[12]同时搜索最小功率谱值, 并根据式(3)和式(4)持续更新 ${S_{\min }}(k,l)$ 和 ${S_{\min }}'(k,l)$ 以及 ${S_{{\rm{tmp}}}}(k,l)$ 和 ${S_{{\rm{tmp}}}}'(k,l)$ . 在噪声估计更新中会根据上一节VAD算法所给出的话音存在标记来选择大窗或小窗下所搜索到的最小功率谱值, 从而实现变窗长搜索. 本文算法大窗L长度选用50帧、小窗L长度选用8帧.

2.4 噪声估计更新

若话音帧通过上述的双参数双门限VAD算法被标记为“语音存在”, 则根据式(5)计算当前帧平滑功率谱 $S(k,l)$ 与大窗下的最小功率谱值 ${S_{\min }}(k,l)$ 的比值 ${S_{{r}}}(k,l)$ . 若被标记为“话音不存在”, 则根据式(5)计算当前帧平滑功率谱 $S(k,l)$ 与小窗下的最小功率谱值 ${S_{\min }}'(k,l)$ 的比值 ${S_{{r}}}(k,l)$ . 将 ${S_{{r}}}(k,l)$ 与经验值 ${\rm{sigma}}$ 比较, 确定 $I(k,l)$ , 最后根据式(6)和式(7)求得噪声估计值 ${\lambda _d}(k,l)$ .

由于小窗长度较短, 选用小窗下搜索到的最小功率谱值来进行噪声估计更新计算, 会加快噪声估计速度.

3 话音估计器

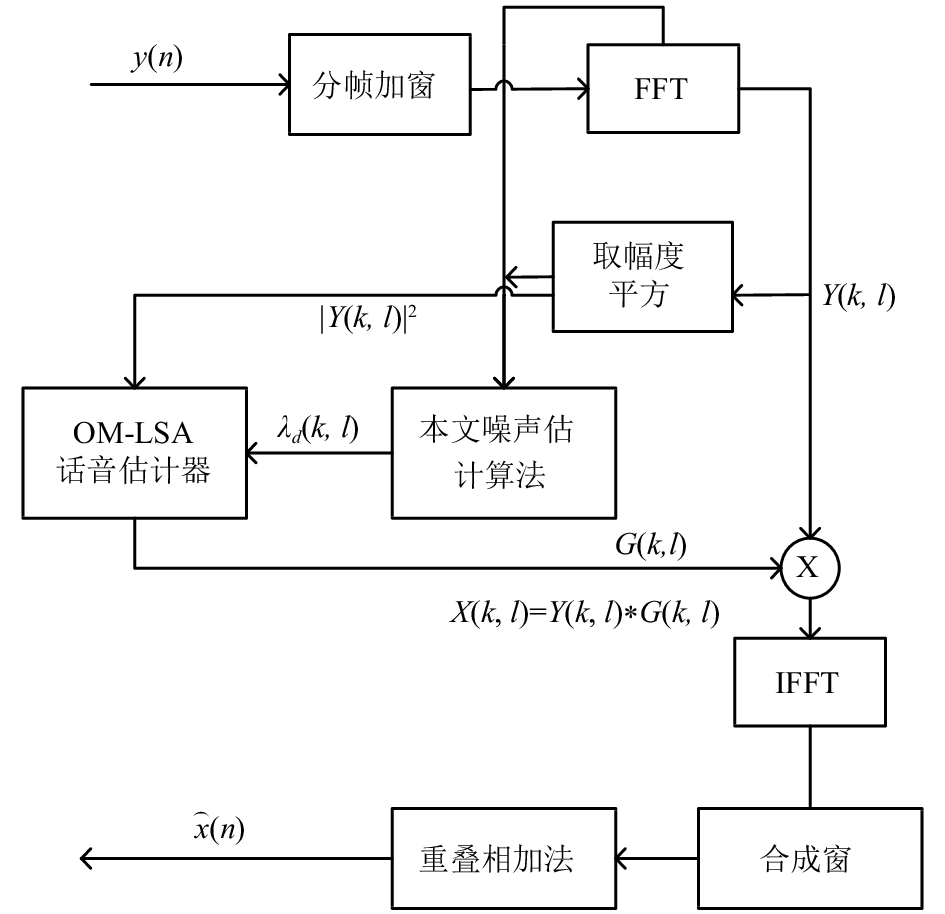
本文采用Israel Cohen提到的OM-LSA话音估计器^[13], 结合本文的改进型噪声估计算法, 实现整个语音增强算法, 具体框图如图2所示.

图2中的 $y(n)$ 为带噪话音, 加窗分帧后经过FFT, 求得带噪话音的频谱 $Y(k,l)$ , 幅度谱 ${\rm{|}}Y(k,l{\rm{)}}{{\rm{|}}^2}$ , 并通过本文算法求得噪声估计值 ${\lambda _d}(k,l)$ . 实验中分帧长度为32 ms, 重叠帧长度为16 ms.

文献[13]中指出: 通过估计每一个频率子带话音存在概率, 得到一个联合时频特性的增益函数:

$G(k,l) = {(\frac{{\xi (k,l)}}{{1 + \xi (k,l)}})^{p(k,l)}}G_{\min }^{1 - p(k,l)}$

(16)

其中 $\xi (k,l)$ 是第 $l$ 帧第 $k$ 个子频带的先验信噪比, $p(k,l)$ 是第 $l$ 帧第 $k$ 个子频带的话音存在概率, 均根据噪声估计得到的噪声谱值来求解, 具体求解方式参考文献[13], 此处不做详细讨论.

通过下式求得处理后的话音频谱:

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} (k,l) = Y(k,l) * G(k,l)$

(17)

其中, $\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over X} (k,l)$ 为处理后的话音频谱, 最后通过IFFT快速傅里叶反变换得到时域表达式 $\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over x} (n)$ , 合成输出得到最终处理结果.

4 实验仿真

本节的实验仿真内容主要为: 将引入双门限双参数VAD辅助算法的变窗长改进算法与原MCRA算法^[2]做对比, 比较收敛时间长短. 实验中的噪声类型采用选自Noisex中的高斯白噪声, 以及超短波噪声, 然后分别将高斯白噪声、超短波噪声与纯净语音叠加, 生成几段样本用来测试. 实验选取标准普通话测试话音17 s, 采样率8 KHz.

4.1 实验设计

实验一. 选取上述纯净话音样本, 给样本加上高斯白噪声, 带噪话音8 s–11 s处信噪比由10 dB变为2 dB, 在语谱图3(a)中用方框标出, 并用文字说明. 图3(b)为原MCRA算法在噪声谱陡增时的噪声估计延迟, 图中用方框标示, 可以看到噪声估计延迟较长, 约为1.6 s; 而图3(c)为本文改进算法的语谱图, 可看到噪声谱陡增处, 噪声估计延迟缩短, 约为0.4 s.

实验二. 选取上述纯净话音样本, 给样本加上超短波噪声, 此环境下噪声谱陡增段包含话音, 在2.5 s–4 s处, 信噪比由10 dB变为0 dB, 语谱图4(a)中用方框标出, 并用文字说明. 图4(b)中可以看到, 噪声估计延迟约为1.5 s; 而图4(c)为文中改进算法的语谱图, 可以看到噪声谱陡增处, 噪声估计延迟缩短, 约为0.5 s.

4.2 实验结果分析

从图3和图4中, 可以看出: 无论是在高斯白噪声还是超短波噪声环境下, 本文提出的改进型算法, 面对噪声谱陡增, 噪声估计延迟都要比原MCRA算法短, 即噪声估计速度本文提出的算法要优于原MCRA算法.

5 总结

本文利用了过零率对噪声功率谱变化不敏感的性质, 将能零比与最大对数似然比结合, 作VAD辅助检测. 联合原有算法, 采用大小窗同时搜索功率谱最小值, 最终形成基于变窗长搜索的改进型噪声估计算法. 经过实验证明, 改进的噪声估计算法, 在噪声谱陡增时, 能够有效的降低噪声估计延迟.