2. 中国科学院 沈阳计算技术研究所, 沈阳 110168
Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China
粉末衍射仪是物质研究的常用仪器, 通过试样对射线在不同角度的衍射强度分析, 达到识别物质类型等目的. 粉末衍射仪多使用单点探测器, 执行一次Theta-Theta扫描用时常达到几十到数百分钟[1]. 而使用一维阵列探测器的粉末衍射仪可以将作业时间大大减少, 根据探测器的探测单元数量不同可将时间缩短几十甚至几百倍. 基于一维阵列探测器的X射线粉末衍射仪的开发是我所承担的“X射线单晶衍射仪操作与控制系统”国家重大科学仪器设备开发专项的延伸任务. 该设备结构复杂、探测单元数量多, 使用的探测器型号为MYTHEN2 R 1D, 含有640个探测单元, 常有数据偏差问题需要处理. 以往的方法虽然也能判断问题的原因, 但效率不高且对专家依赖. 这不仅造成了高昂的维护成本, 还降低了仪器可用性. 因此在系统出现数据质量问题时能够快速的判断偏差的原因可以提高效率及设备可用性. 该系统的功能是针对设备数据精度偏差原因进行自动化的分析, 有其实际应用价值. 同时该系统的模型和流程有较强通用性, 在单晶衍射仪等其他衍射仪器的辅助校正中仍可通用, 在应用不同的特征提取方案后可在其他衍射仪器的辅助校正中较好应用. 本文首先对粉末衍射仪可能出现导致数据质量的问题进行分析, 然后介绍了系统的核心数据处理流程和模型训练方法.
1 数据偏差现象及原因分析通过大量理论研究及工程实践经验总结, 使用一维阵列探测器的粉末衍射仪主要存在以下几方面的数据偏差[2–4].
1.1 强度偏差出现总体或部分衍射值明显区别于正常的情况. ① 死点和热点, 即某探测单元衍射值永远低或者永远高, 已通过阵列探测器的平场校正、坏点校正技术进行预处理; ② 射线源射线强度强或者弱, 造成衍射值系统性的偏高或偏低; ③ 射线源射线强度不稳定供电电压不稳定等, 造成衍射数据不稳定的偏差.
1.2 角度偏差出现波峰位置或者形状与正常情况偏差较大的现象. ① 测角仪初始位置偏移, 造成衍射数据出现类似左平移或者右平移的现象; ② 探测模块移动装置移动角度不准, 造成数据在移动后模块交界处出现明显位移偏差, 此文称之为模块间偏差; ③ 模块内探测单元的位置出现偏差.
1.3 偏心偏差由于样品不在圆心位置或者探测器运动轨迹非正圆, 造成数据沿角度轴伸展或收缩的情况.
2 偏差判断X射线粉末衍射仪是十分精密的科学仪器, 偏差数据出现概率小, 如果给每份数据进行全部的系统操作是不经济的, 偏差判断部分主要是筛选可能存在偏差的数据, 大大降低系统工作量. 偏差判断流程如图1所示. 另外本文实验数据为设备出厂数据, 偏差率大于应用中数据.
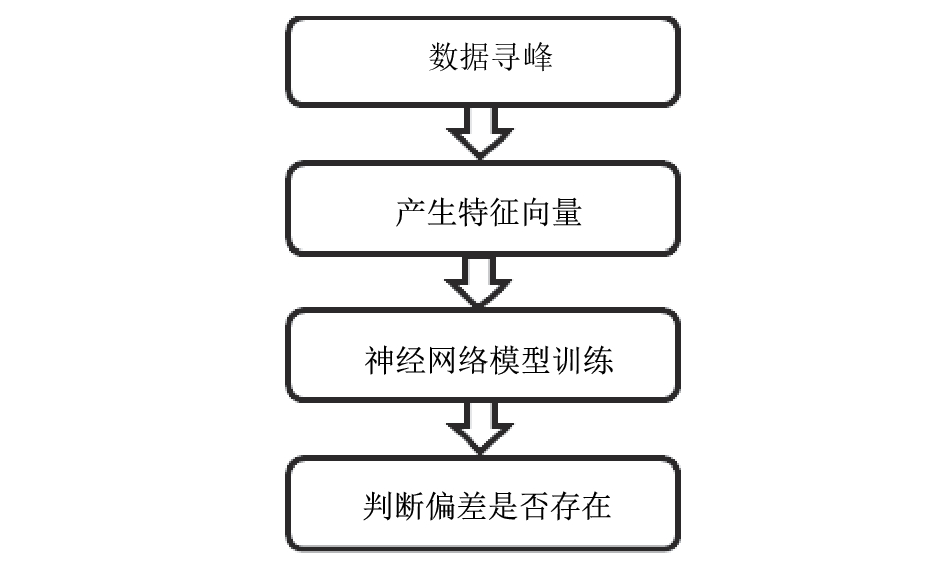
|
图 1 偏差判断流程 |
2.1 数据描述
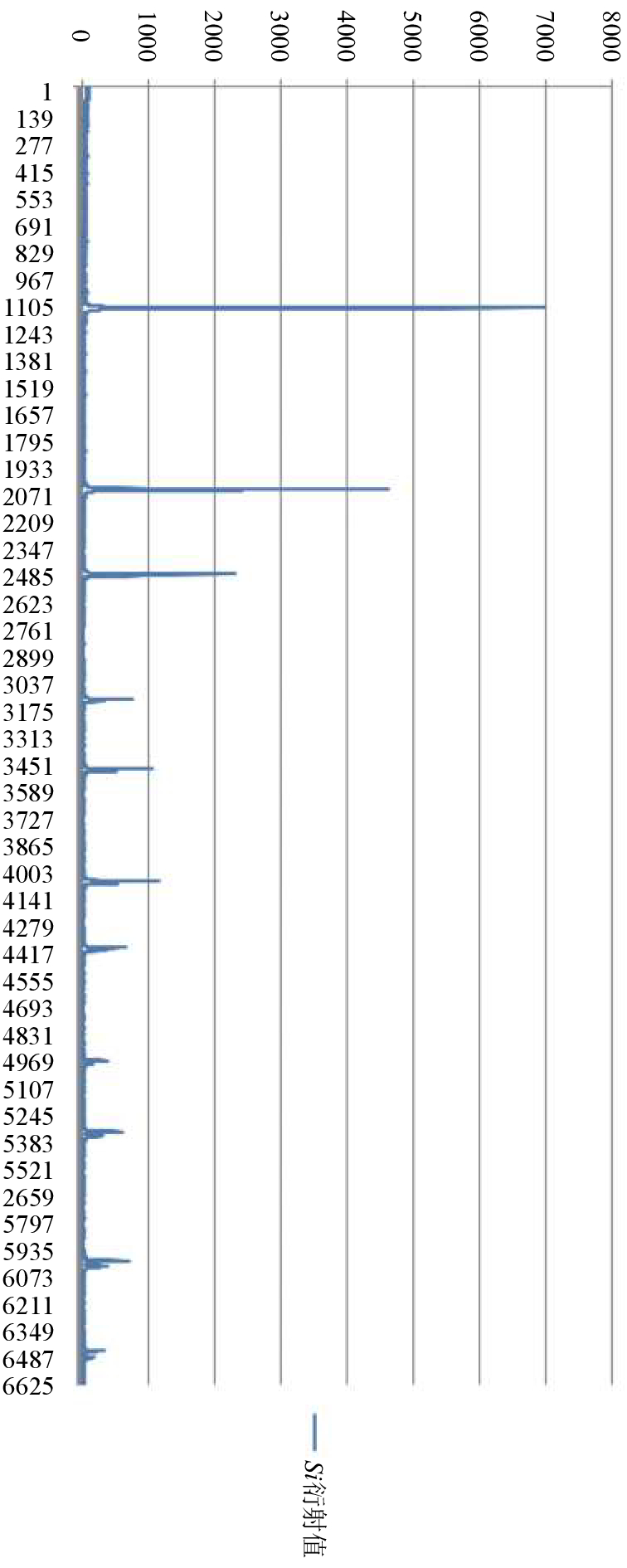
本文通过分析试样衍射数据, 识别衍射仪是否存在偏差及存在何种偏差. 本文选用X射线粉末衍射仪样机的实验数据作为偏差识别的基础数据集, 选用了试样硅粉(Silicon powder, SRM 640c)的衍射数据, 且已进行偏差的标注, 共7829组实验数据. 因仅用于训练上文分析的问题, 其他问题暂不讨论, 所以已经去掉有其他偏差的数据. 每个数据文件为一个硅粉样品进行一次Theta-Theta扫描的衍射数据, 实验扫描角度135°, 步宽为(探测单元间的角度差) 0.02°. 正常数据曲线拟合后如图2所示.
基于X射线与晶体相遇的衍射现象及衍射原理并结合衍射数据我们可知, 衍射数据特征主要体现在其衍射峰上. 所以特征提取工作也着重针对波峰进行, 但在提取波峰特征之前先需要时使用寻峰算法确定每个峰的位置.
2.2 寻峰此处的寻峰主要是对衍射峰进行定位, 为防止噪声影响, 强度限制应该是动态决定于总体衍射强度(用快速查找的变形找中位数). 简单寻峰是一种在相邻的衍射点中寻找极大点的寻峰方式, 计算简单, 而且得出的位置也最为准确, 适合衍射峰定位. 窗口大小可根据不同试样调整, 以硅粉为例可以定为200, 找出大于强度限制的连续区域 (连续超过n个点) 即可对衍射峰定位. 无此区域则移动窗口起始位置到原窗口结束处, 此区域以窗口结束位置结尾则将窗口起始位置移动到这段区域开始处, 否则确定衍射峰开始位置Ss、峰值位置Sp、峰值p及结束位置Se. 寻峰后将衍射峰数量与X射线衍射标准数据库数据对比, 如果不同可以直接判断射线源存在明显强度波动问题需要重新调试. 每一组得到44个数据构成44维的特征向量.

|
图 2 硅粉试样标准衍射值 |
2.3 BP神经网络模型
BP神经网络实质上实现了一个从输入到输出的映射功能, 而数学理论已证明它具有实现任何复杂非线性映射的功能. 这使得它特别适合于求解内部机制复杂的问题. 该功能输入特征为峰位、峰强, 维度达到44, 44维特征综合影响结果, 内部机制复杂, 适合使用神经网络模型; BP神经网络能通过学习带正确答案的实例集自动提取“合理的”求解规则, 具有自学习能力, 正好适合此处输出0到1的连续值用于判断此时状态存在偏差的可能性.
此BP神经网络判断模型是一个44输入、单输出的神经网络. 输入变量为上文的44维特征向量记为[x1, x2,…, x44], 因为强度值及位置值度量不同、范围大, 所以预处理中将所有特征值都进行归一化操作[5]; 输出变量为y, y为一个0到1之间的小数, 代表本组数据为偏差数据的可能性, 越接近1则此组数据属于有偏差数据的可能性越大, 否则为正常数据的可能性越大, BP神经网络输出后可设置不同阈值用来区分是否为偏差数据, 为保证筛选偏差数据的召回率, 此阈值可以根据需求调整; 期望输出为t(无偏差数据为0, 有偏差数据为1), 具有2层隐含层, 包含20个隐层单元[6,7].
对于第i个样本, 该模型各神经元误差定义为:
| $E(i) = \frac{1}{2}{\left[ {t(i) - y(i)} \right]^2}$ | (1) |
公式(2)为激励函数采用sigmod函数:
| $f\left( x \right) = \frac{1}{{1 + {e^{ - x}}}},\;\;{f^,}\left( x \right) = f\left( x \right)\left( {1 - f\left( x \right)} \right)$ | (2) |
其中, w为梯度, b偏置值, 出于保守起见它们的修正都取0.01. 公式(3)和公式(4)分别是隐层1第j个神经元和隐层2第k个神经元的输入输出计算公式.
| ${N_j} = \sum\nolimits_{p = 1}^{44} {{w_{jp}} * {x_p} + {b_j}} ,f({N_j})$ | (3) |
| ${n_k} = \sum\nolimits_{p = 1}^{20} {{w_{kp}} * f({N_p})} + {b_k},f({n_k})$ | (4) |
该神经网络模型如图3所示.

|
图 3 偏差判断神经网络模型 |
模型训练中随机抽取数据中的4000组数据, 剩余3829条数据用于模型效果测试.
3 偏差识别在使用神经网络模型判断数据存在偏差后还要进一步识别偏差类型和程度, 可以结合仪器特点及统计学知识确定一些可量化指标, 来对偏差进一步识别. 偏差识别流程如图4所示.

|
图 4 偏差识别流程 |
3.1 基于知识的特征处理
首先获取标准衍射数据, 根据多个此试样正常衍射数据通过衍射强度平均得到, 以此为计算标准. 角度偏差会造成峰位偏差, 偏心偏差可造成波形沿横轴的伸缩, 例如测角仪初始化位置偏移可能造成衍射峰位置出现系统性偏差如图5所示.
所以选取峰位差这一变量, 计算每个峰的起始位置、峰值位置和结束位置峰位差, 如公式(5):
| $\left\{ \begin{aligned}&\Delta {S_s} = {S_s} - S_s'\\&\Delta {S_p} = {S_p} - S_p'\\&\Delta {S_e} = {S_e} - S_e'\end{aligned}\right.$ | (5) |
随机抽取结果验证, 发现正常数据ΔS值都很小, 而异常数据ΔS值总有一些明显较大的情况, 所以ΔS值的选取是有代表性的. 根据前面的偏差介绍, 角度偏差及偏心偏差造成的峰位差变化情况适合区分问题原因. 将相对模块起始位置及ΔS作为点对用曲线拟合的方式来研究数值变化情况. 根据最佳拟合曲线的类型和参数可对偏差原因进行有效判断. 先针对模块内进行操作, 用二次函数拟合. 常数项A0, 一次项参数A1, 二次项参数A2, 选取这样的函数拟合主要在于A0体现初始化位置问题, A1体现位置差的线性变化多为探测单元间隔不合理导致需要更换模块, A2可以体现模块倾斜等造成的偏心偏差 (因单模快倾斜区域小, 不会造成伸展及收缩规律两次变化的情况).
模块间的位置偏差会造成模块间位置差出现跳跃性变化, A0为每个模块起始偏差, 并根据以上模块内拟合函数计算模块结束位置偏差Ae, 见公式(4):
| $\Delta {a_i} = {A_{0(i + 1)}} - {A_{ei}}$ | (6) |
计算每个模块间偏差, 因为此处为单模块移动所以Δai的综合统计值可以很好的体现这一问题, 计算平均值E(|Δai|)和方差D(Δai), 这样即体现其绝对误差由可以体现其不稳定性.
|
图 5 硅粉试样位置偏差衍射值 |
偏心偏差体现在位置特征的放缩, 需要对所有位置与位置差点对进行综合分析. 考虑到模块内部的局部位置偏差会干扰大的放缩趋势, 此分析仅在无模块内部偏差问题时才进行. 对这些点对位置值按照模块间偏差Δai进行修正, 去除模块移动装置问题影响, 再用三次函数拟合, 各次项参数分别为B0、B1、B2、B3. 注意这里使用三次函数, 因为拟合的范围为135°可能出现先收缩再放大再收缩或者相反的情况. B2和B3可体现偏心偏差, B0和B1则和A0、A1类似.以参数A0、A1、A2、E(|Δai|)、D(Δai)、B0、B1、B2、B3训练分类模型来达到四个二分类的目的, 分别是是否有模块内偏差、是否有初始化偏差、是否有模块间偏差、是否有偏心偏差.
强度差则可以体现强度偏差, 例如当射线源出现波动时数据可能如图6所示.
为便于后续操作使用相对强度差公式为:
| $\Delta H = \frac{{\left( {{H'} - H} \right)}}{H}$ | (7) |
强度差计算的前提是对应角度对应, 所以需要先做好位置的匹配. 所以判断各种角度及偏心偏差后需要对经过Δai修正后数据进行一些放缩处理. 为保证关键位置的准确性使用ΔS特征序列对峰位进行纠正, 以这些特特征位置为基准两两之间中间采用补点和去点的方式来进行放缩. 补充或去除的点按照平均分布的方式选择, 例如两个特征点中间有100点, 需要去除其中5个, 采用隔19点去除一点数据的方式, 补充点的值简单取其相邻两点值平均数即可. 没有选取拟合函数进行放缩是因为此处使用的是以最小二乘法为基础的多项式拟合, 是一种“平均通过式”的拟合, 可以较好体现总体规律但局部准确性不一定高.
进行位置对齐后计算相对强度差. 将相对强度差的绝对值与阈值δ比较, 区分是否在可允许的强度误差范围内, δ为一个较小的小数比如0.05, 计算超过此范围的点比例r作为一个参数. 因强度问题主要由射线源引起, 射线源强度可能有偏高、偏低、波动或其他不稳的情况, 以上相对强度偏差的变化情况正好可以体现射线源强度变化情况. 使用公式(8)来计算.
| $X = {C_0} + {C_1} * \sin ({C_2} * T + {C_3}) + {C_4} * T$ | (8) |
进行拟合, T为位置值. C0表现射线源强度偏高或者偏低, C4表现射线源线性变化趋势, C1、C2、C3体现射线源强度可能存在的周期变化问题(电源电压变化易体现此种变化规律). 以参数r、C0、C1、C2、C3、C4为参数训练分类模型, 完成三个二分类, 分别是强度是否偏强或偏弱、强度是否周期波动、强度是否有其他不稳情况.

|
图 6 硅粉试样强度偏差衍射值 |
3.2 分类树模型
经过以上的分析及处理, 各特征都针对某相关性较高的问题, 分类的目标明确过程可解释性强, 而分类树模型计算量小、处理简单, 比较适合做此分类. 7个二分类每个限制分类树层高在4层以内, 提前做到剪枝的效果. 采用C4.5算法[8], 使用增益率 (gain ratio) 来选择分裂属性, 选择增益率最高的属性作为分裂属性. 我们假设将训练元组D按属性A进行划分, C4.5算法首先定义了“分裂信息”, 其定义为:
| $split\_inf {o_A}(D) = - \sum\nolimits_{j = 1}^x {\frac{{|{D_j}|}}{{|D|}}} {\log _2}(\frac{{|{D_j}|}}{{|D|}})$ | (9) |
增益率定义为:
| $gain\_ratio(A) = \frac{{gain(A)}}{{split\_\inf o(A)}}$ | (10) |
因为此模型用于识别具体偏差类型, 故抽取数据集中存在待分析偏差的1427条, 取800条分别对7个二分类进行训练, 剩余627条作为测试集.
4 结论实验结果表明本文设计的X射线粉末衍射仪智能辅助校正系统可以准确有效地判断偏差原因. 为X射线粉末衍射仪的校正提供了很好的支持. 判断是否存在偏差时, 在设置召回率为95%的情况下从3829条测试数据 (691条偏差数据) 中筛选出1015条可能的偏差数据, 准确率仍高达64.63%. 每个2分类测试集627条数据, 是否存在模块内偏差的测试结果如表1.
| 表 1 是否存在模块内偏差测试结果 |
其他具体结果不再赘述, 准确率和召回率如表2.
系统对各种偏差的判断效果虽不相同, 但都基满足应用需求, 部分偏差判断效果良好. 本文主要提出X射线粉末衍射仪智能辅助校正系统, 并对其核心内容进行叙述说明. 下一步将继续进行模型优化工作, 进一步提升系统准确性; 同时针对其他衍射仪器确定不同的特征提取方案, 进一步扩展系统的应用范围, 将系统应用到其他衍射仪器的辅助校正上.
| 表 2 各种偏差识别的准确率及召回率 |
| [1] |
马礼敦. X射线粉末衍射仪性能的评估. 上海计量测试, 2007, 34(2): 10-15. |
| [2] |
胡丽华, 张勇, 唐娟, 等. X射线粉末衍射仪的测试及使用. 化学工程师, 2012, 26(1): 16-17, 20. |
| [3] |
Gozzo F, Cervellino A, Leoni M, et al. Instrumental profile of MYTHEN detector in Debye-Scherrer geometry. Zeitschrift für Kristallographie, 2010, 225(12): 616-624. DOI:10.1524/zkri.2010.1345 |
| [4] |
Du R, Cai Q, Chen ZJ, et al. Mythen detector for X-ray diffraction at the Beijing synchrotron radiation facility. Instrumentation Science & Technology, 2016, 44(1): 1-11. |
| [5] |
柳小桐. BP神经网络输入层数据归一化研究. 机械工程与自动化, 2010(3): 122-123, 126. |
| [6] |
禹建丽, 卞帅. 基于BP神经网络的变压器故障诊断模型. 系统仿真学报, 2014, 26(6): 1343-1349. |
| [7] |
邓万红, 籍艳, 王平. BP神经网络在诊断气象仪故障的研究. 科技创新与生产力, 2014(9): 68-69. |
| [8] |
王继强. C4.5算法在信号设备故障诊断中的应用研究. 电子世界, 2012(9): 107-109. |
 2018, Vol. 27
2018, Vol. 27



