在电子商务蓬勃发展的信息化时代, 越来越多的互联网用户在线评价自己的消费, 这些文本的评论信息作为消费者亲身体验的反馈, 涵盖了大量的有用信息. 一方面以往消费者对产品的评价可以帮助潜在消费者事前对产品有所了解, 便于消费者根据自身需要做出消费决策; 另一方面也可以作为反馈信息帮助商家了解消费者的购买意愿、跟踪商品的售后服务等, 进而不断改进、提高自身竞争力.
消费者情感极性分析[1–3](Sentiment Polarity Analysis)是文本分析的一大分支, 一般可以分为积极(Positive)和消极(Negative)两类, 只有准确地把握了消费者的情感极性才能做好客户的维护、挖掘潜在客户、弥补欠缺进而提升自身的市场竞争能力. 本文旨在运用高维数据变量选择方法[4]关注两方面的核心内容, 一方面寻求较好的消费者情感极性预测模型; 另一方面, 以往的研究重在分类预测, 而对评论背后隐含的商业价值很少深入探究, 本文希望借助Lasso算法的变量选择优势挖掘出影响消费者情感极性的关键因素.
1.2 研究现状从国内外研究现状来看, 目前对文本数据的分析主要涉及提取文本特征、文本特征关联分析、文本内容识别, 以及文本情感极性分析等方面. 其中提取文本特征是对文本信息进一步分析的基础, 所谓特征提取就是根据评论文本的分词结果, 选择对文本具有代表性的关键词. 特征选取主要有两种不同的思路, 一种是构造评估函数法[5,6], 另一种是在事先挑选的初始种子集为起点, 对候选特征集合采用不断迭代的方法确定最终的特征集合[7].
以往对特征提取和文本情感极性的分析, 大都以词频和语义分析为主. Hu用形容词作为观点词分析英文评论的情感极性, 借助WordNet将要判断情感倾向的词条与给定情感倾向的同义词或反义词词网相匹配, 词条的情感倾向与同义词具有相同的情感倾向, 与反义词具有相反的情感倾向[8]. Turney以形容词和副词为分析对象, 运用PMI方法分别计算给定词与 “excellent”、“poor”的点互信息(PMI), 两者相减, 若为正值则情感极性为正, 反之为负. 近年来, 部分学者在对词的分析上做了进一步延伸, 如根据词条在不同文本类别间分布不均的情况, 提出了对特征项加权的方法判断情感极性[9]. 随着大数据时代的到来, 相关的机器学习方法在情感极性分析中也越来越受欢迎[10–12]. Pang等根据事先既定的有关形容词的积极词料集和消极词料集, 分别运用朴素贝叶斯(Naive Bayes)、最大熵(Maximun Entropy)和支持向量机(Support Vector Machines)三种方法进行文本的情感极性分析并在不同的情况下进行了对比[13]. 王健等基于主题概率模型(LDA)实现了文本分类, 并取得较好的分类效果[14].
1.3 研究思路以上研究对文本情感极性的预测, 主要有两种思路, 第一种是由特征词或特征项的情感极性加权进行预测; 第二种是运用机器学习方法对文本的情感极性进行预测, 主要包括支持向量机、朴素贝叶斯、最大熵等方法等. 除此之外, 鉴于L1-正则项对高维数据良好的惩罚特性, Lasso稀疏模型已经被成功的应用于文本分类领域[15–19]. 鉴于此, 本文运用Lasso-Logistic和Lasso-PCA模型[20–22]对餐饮业文本评论的情感极性进行分析. 一方面, 作为对比找到更好的分类模型; 另一方面, 笔者借助Lasso-Logistic较好的模型解释能力对影响消费者情感极性的关键因素深入分析. 相比于Lasso-Logistic模型, 目前鲜有对Lasso-PCA模型的应用文献, 基于稀疏数据的主成分模型在解决数据稀疏性的同时, 保留了较多的变量信息, 但该方法对文本的情感极性预测效果有待于探讨.
根据以上文献综述, 本文提出以下研究思路: (1) 对数据进行预处理, 包括提取评论样本、分词等. (2) 运用TF-IDF算法初步提取关键词. (3) 分类预测. 以消费者情感极性为被解释变量, 以高维稀疏关键词词频矩阵为解释变量, 结合Lasso算法, 运用带惩罚的Logistic和PCA两种方法对消费者情感极性进行预测. (4) 借助Lasso的变量选择结果, 运用Logistic模型对显著影响消费者情感的因素做进一步的分析.
2 数据来源与处理 2.1 数据来源本文数据来源为大众点评网上某餐厅的消费者评论的文本内容和评分等级, 共2293条评论记录. 因变量是评论者对消费情况的总体评价的星级数据, 分为5个等级, 1颗星代表最低评价, 5颗星代表最高评价. 考虑到实际情况, 消费者一般倾向于给出较高的星级指数, 在评分为3的样本中大都带有消极的情绪, 如表1所示. 因此, 在分析过程中将1颗至3颗星的样本视为情感极性为负; 将4颗星和5颗星的样本视为情感极性为正. 这里随机抽取了400条积极样本和400条消极样本, 作为对消费者情感极性分析的总样本.
| 表 1 部分样本信息 |
首先提取1000个关键词作为初始特征集, 然后遍历每一条评论的分词结果, 分别统计特征词在每条评论中出现的频数, 以由此得到的稀疏矩阵作为解释变量. 不失一般性, 在分析过程中选用样本的80%作为训练集, 20%作为测试集进行样本外预测.
2.2 数据处理数据处理的第一阶段是利用R软件的加载包jiebaR对网络评论文本进行分词, 首先在分词的过程中去除常用停用词(stop words, 如介词、冠词、限定词等); 同时考虑到分词结果会产生数值型的分词结果, 所以在数据的预处理过程中删除了数值型的分词结果; 最后运用该软件包提供的词频-逆向文本频率算法(TF-IDF)提取关键词, 作为备选特征词集合.
TF-IDF算法是提取文本关键词常用的统计方法, 用以评估一字词对一个文本的重要程度. 其基本思想是如果一个词比较少见, 但是它在这个文档中出现多次, 那么它很可能就反映了这个文档的某方面特性, 可以作为该文档的关键词 . 该算法分为词频(Term Frequency, TF)和逆向文本频率(Inverse Document Frequency, IDF)两部分. TF即一个词在目标文本中出现的频率, 见式(1). IDF是对该词代表的信息量的衡量, IDF值的计算需要一个词料库, 由词料库中总文件数除以包含该词的文档数, 再将商取对数得到, 见式(2). TF - IDF值即TF与IDF的乘积, 见式(3). 这里选用的是R软件jiebaR包自带的词料库.
| $tf\left( {t,d} \right) = \frac{{{n_{t,d}}}}{{\sum\nolimits_k {{n_{k,d}}} }}$ | (1) |
| $idf\left( {t,D} \right) = \log \frac{N}{{\left| {\left\{ {d \in D:\;t \in d} \right\} + 1} \right|}}$ | (2) |
| $TF - IDF = tf\left( {t,d} \right) \times idf\left( {t,D} \right)$ | (3) |
其中, nt,d是词t在文档d中出现的频率; N代表词料库中的文件数, N = |D|; |{d∈D: t∈d}|代表词料库中包含词t的文档数, 为避免该词不在词料库中的情况, 将|{d∈D: t∈d}|+1作为分母.
运用TF-IDF算法可以得到对文本内容具有代表性的关键词, 根据文本的分词结果统计出1000个关键词的词频矩阵, 如表2所示. 从表中可以看出, TF-IDF值较大有“水煮鱼”、“川菜”、“味道”和“毛血旺”、“宫保鸡丁”等名词性词汇, 以及“不错”、“好吃”和“喜欢”等带有情感极性的形容词、副词和动词.
| 表 2 部分关键词词频矩阵 |
此外, 从词频的角度来看, “味道”、“不错”的频率明显高于“水煮鱼”和“川菜”; 但是从IF-IDF值来看, “水煮鱼”和“川菜”的值则高于“味道”、“不错”. 这是因为, “味道”和“不错”出现的频率虽然高, 但是对文本内容的代表性不够, “水煮鱼”和“川菜”则直接反映出了文本的主题, 具有更好的代表性. 同时可以看出, “水煮鱼”和“毛血旺”、“宫保鸡”具有较高的频数和TF-IDF值, 且“水煮鱼”高于“毛血旺”和“宫保鸡”, 说明这三个菜品在该家餐厅中比较具有特色, 尤其是“水煮鱼”, 建议作为餐厅的特色菜来打造. 同时也说明了以表2的关键词词频矩阵作为解释变量对文本的情感极性进行预测和分析, 既很好的将文本型数据转化为数值型数据又不失对文本内容的代表性.
3 消费者情感极性的预测模型 3.1 Lasso-Logistic预测模型从表2的关键词词频矩阵可以知道, 解释变量具有明显的高维性和稀疏性的特点. 由于关键词数目过多, 且大部分数据为0, 为解决自变量矩阵中存在的奇异问题, 必须首先对数据进行降维, 这也是将Lasso算法运用到Logistic回归和主成分回归的根本出发点.
Lasso算法加入的惩罚项为L1范数, 即参数向量中各个元素绝对值之和, 由两部分构成, 一部分为Logistic回归的负对数似然函数, 另一部分为L1-正则项, Lasso的目的是求得使f(β)最小的解, 即式(4)所示.
| $\hat \beta = \arg {\min _\beta }\left\{ {\sum\limits_{i = 1}^n {\log \left( {1 + {{\rm{e}}^{ - {y_i}x_i^{\rm{T}}\beta }}} \right)} + \lambda \sum\limits_j^p {\left| {{\beta _j}} \right|} } \right\}$ | (4) |
关于λ的选择, 这里运用的是10折交叉验证的方法[23–25]. 本文借用R软件中软件包glmnet来实现Lasso算法, 如需程序代码, 可向作者索取.
由于Lasso算法中λ的取值具有一定程度的随机性, 因此每次提取出的关键词的个数并不相同, 为了不影响预测结果, 经过几次实验发现, 在提取大于1000个关键词时Lasso的稀疏解的个数没有明显增加, 所以最终提取了TF-IDF值较大的前1000个关键词词频作为初始解释变量. 由Lasso算法运用(4)式得到稀疏解, 然后将得到的系数不为0的关键词提取出来, 作为最终Logistic回归的解释变量对消费者的情感极性进行预测. 模型预测效果见表3和图1.
| 表 3 Lasso-Logistic预测效果混淆矩阵 |
|
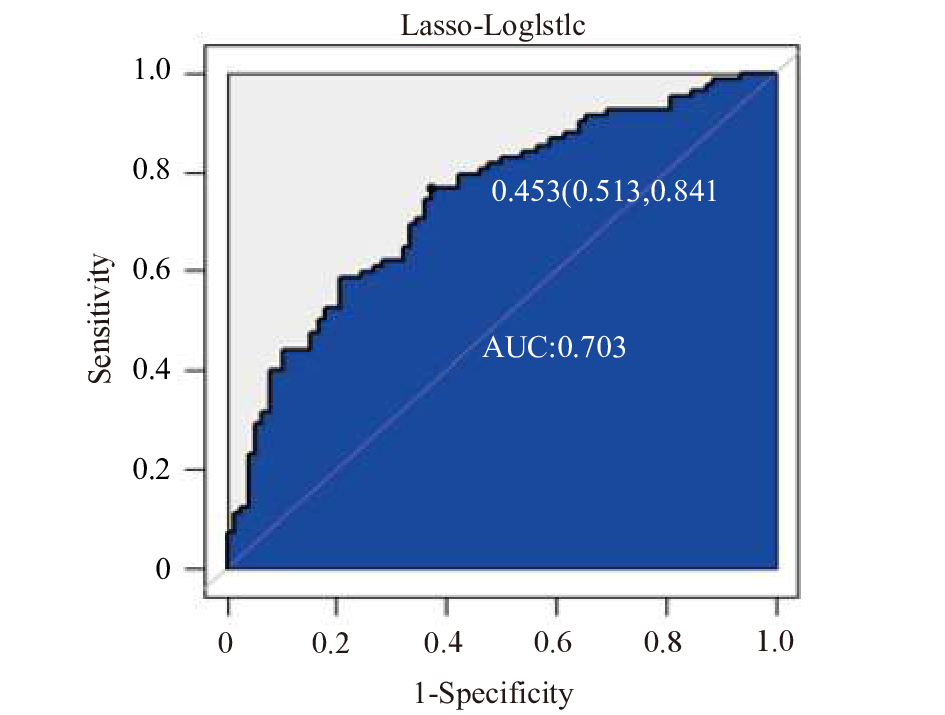
图 1 Lasso-Logistic预测结果的ROC曲线 |
表3列出了在分类阈值设为0.5时由Lasso-Logistic模型得到的测试集预测结果的混淆矩阵, 根据混淆矩阵可以得到, 模型对测试集预测精度为65%; 同时由表3纵向比较结果可以得出, 预测结果的敏感性(True Positive Rate, TPR)和特异性(False Positive Rate, FPR)分别为0.66和0.36, 分别刻画的是正确预测为正类占真实值中正类的比例、分类器错认为正类的负实例占所有负实例的比例, 如式(5), (6)所示.
| $TPR = \frac{{TP}}{{TP + FN}}$ | (5) |
| $FPR = \frac{{FP}}{{FP + TN}}$ | (6) |
为了更好的体现出模型的预测效果, 这里采用ROC曲线下面积(AUC)来评价模型的预测效果. 从图1中可以看出, 模型预测得到的AUC值为0.703, Lasso-Logistic预测方法在基于文本评论的消费者情感极性的分析上是有效的.
3.2 Lasso-PCA预测模型主成分分析(Principle Components Analysis, PCA)可以直接通过矩阵的奇异值分解(PMD)得到, 如式(7)所示. 具体来说, 是通过对原始变量进行一个基的变换, 实现变量的重新组合, 组合后得到的p个新的变量称为主成分, 前r (r<p)个主成分携带了原始变量X的主要信息. 主成分分析的优良特性使其在数据降维方面得到的广泛的应用, 然而在高维数据, 尤其是稀疏的高维数据的情况下, 传统的主成分分析的求解受到挑战. 因此, 本文借鉴文献[22]提出的SPC方法, 通过对V施加惩罚, L1-正则项, 运用PMD(·, L1)来实现高维稀疏矩阵的主成分分析[22].
| ${\bf{X}} = {\bf{UD}}{{\bf{V}}^{\rm{T}}},{{\bf{U}}^{\rm{T}}}{\bf{U}} = {{\bf{I}}_{{n}}},{{\bf{V}}^{\rm{T}}}{\bf{V}} = {{\bf{I}}_{{p}}},{d_1} \ge {d_2} \ge \cdots \ge {d_p} > 0$ | (7) |
| $\begin{array}{l}{\rm{maximiz}}{e_{{u_{k,}}{v_k}}}u_k^{\rm{T}}{\bf{X}}{v_k}\\{\rm{s.t.}}\;\;{\left\| {{v_k}} \right\|_1} \le c,\left\| {{u_k}} \right\|_2^2 \le 1,\left\| {{v_k}} \right\|_2^2 \le 1,{u_k} \bot {u_1}, \cdots ,{u_{k - 1}}\end{array}$ | (8) |
R软件提供的PMA软件包提供了很好的分析工具. 为了使模型具有可比性, 这里的主成分分析沿用上文中Lasso-Logistic预测模型抽取的测试集和训练集, 选取与Lasso-Logistic预测模型的变量相同数目的主成分, 将Lasso-PCA得到的稀疏主成分作为解释变量, 运用Logistic回归对消费者的情感极性进行预测, 模型预测效果如表4和图2所示.
| 表 4 Lasso-PCA预测效果混淆矩阵 |
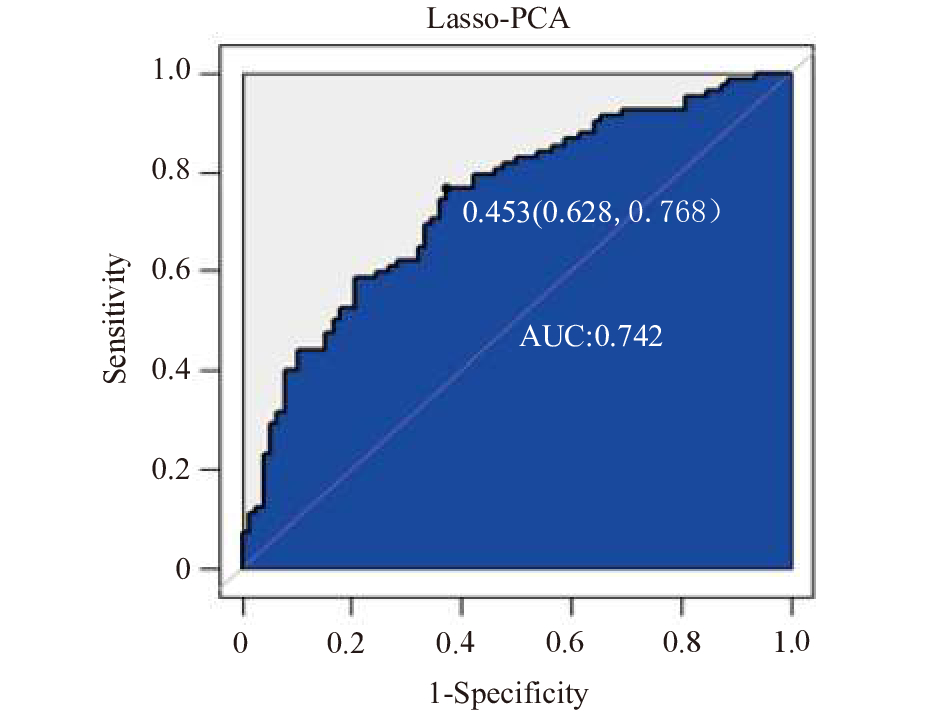
同样地, 根据模型的预测结果可以得到Lasso-PCA对测试集预测混淆矩阵, 如表4所示. 根据表4可以得到, 模型对测试集样本预测的正确率为67.5%, 灵敏性和特异性分别为0.71和0.36. 因此, 和Lasso-Logistic模型相比, Lasso-PCA模型具有更高的预测精度和灵敏性. 仍然采用ROC曲线来进一步评价模型的预测结果, 如图2所示. 本次抽样得到的Lasso-PCA模型的AUC值为0.742, 略高于Lasso-Logistic模型的AUC值0.703. 综合以上分析来看, Lasso-PCA模型对基于文本评论的消费者情感极性的预测是有效的, 并且初步判断Lasso-PCA模型比Lasso-Logistic模型具有更好的预测效果.
|
图 2 Lasso-PCA预测结果的ROC曲线 |
3.3 两种预测模型的比较
以上关于Lasso-Logistic模型和Lasso-PCA模型的比较建立在一次抽样的基础上, 由于每次抽样都是随机的, 因此以上关于模型的比较也具有一定的随机性, 为了更好的比较两个模型的预测效果, 本文对以上研究过程重复100次, 分别得到Lasso-Logistic模型和Lasso-PCA模型的100个AUC值, 比较结果如图3所示.
|
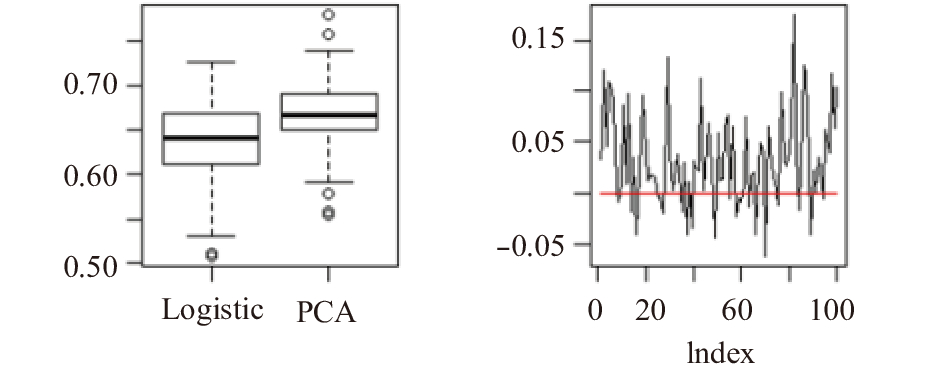
图 3 两种预测模型预测效果比较 |
图3呈现出了100次实验得到的预测结果的AUC值. 由图3(a)的箱线图可以看到, Lasso-PCA模型的预测精度的平均值略高于Lasso-Logistic模型预测精度的平均值, 其中Lasso-PCA模型得到的AUC的均值0.667, Lasso-Logistic模型得到的AUC的均值为0.635. 对每次抽样的预测精度求差, 由Lasso-PCA模型的预测精度减去Lasso-Logistic模型的预测精度, 两者差值如图3(b)所示. 二者差值虽然在0的两侧都有分布, 但上侧明显高于下侧且上侧的值的分布更密集, 说明Lasso-PCA模型的预测精度相对高于Lasso-Logistic模型的预测精度.
4 消费者情感极性的影响因素分析文本评论呈现了消费者对消费行为较为细致的评价, 也是评分的根本依据, 主要由评价对象和对评价对象的情感倾向两部分组成. 从餐饮业的角度来看, 影响消费者情感极性的因素有很多, 包括味道、服务、环境、地理位置、心理预期等等. 探索这些因素是如何影响消费者评价的, 对商家提高服务质量、改善营销策略具有非常重要的意义.
Lasso-PCA模型虽有较好的预测效果, 但模型的解释能力欠佳, 因此, 考虑到Lasso-Logistic模型较强的解释性, 本文借助Lasso-Logistic预测模型变量选择的结果进一步对影响消费者情感极性的影响因素进行分析. 由于Lasso-Logistic模型中由Lasso算法得到的稀疏解具有一定的随机性, 本文进行了两次回归以减小随机性对结果的影响. 这里主要关注回归结果中显著的变量, 结果如表5所示.
| 表 5 两个Lasso-Logistic回归的结果 |
表5呈现出了回归结果中显著变量的相关信息, 从表中可以看出, 两次回归得到的显著性变量存在很大的相似性. 两次回归都得到了25个显著变量, 其中有23个变量在两个回归结果中同时显著. 此外, 从回归系数可以看出, 所有在两次回归中同时显著的变量具有相同的正负号, 且系数大小相差不大, 说明模型具有很好的稳健性. 这些显著的特征词或特征项隐含了影响消费者情感极性的重要因素, 按照属性不同可以将其分成6类, 如表6所示.
| 表 6 显著的回归变量分类 |
三类带有情感倾向的词汇和三类表示特征属性的词汇分别从不同角度体现了消费者情感极性. 从总体上来说, 带有情感色彩的词汇最能直观地表达消费者的情绪; 虽然影响餐饮业消费者情感极性的因素众多, 但是餐厅“特色”、“服务和环境”却是消费者最为关注的; 通过关注含有“下次”、“值得”和“每次”的评论, 可以有效识别潜在消费能力. 具体地, 从以下5个方面进行分析.
(1) 从两次回归结果中可以看出, “不错”、“喜欢”、“好吃”以及程度副词“非常”和“最好”的系数在两个回归中的系数都显著为正. 相比之下, “没有”、“不会”和“一次”这类含有负面情绪的词汇, 回归系数显著为负. 这一结果也是符合常理的, 好的评价对应高的评分; 而对于没有达到满意的消费行为, 消费者往往对不满意之处吐槽, 评分自然也低.
(2) “中规中矩”、“还算”和第一个回归中“还行”的系数显著为负, 说明评论中出现“中规中矩”、“还算”这两个词汇的消费者对消费行为更加倾向于持负面的态度, 服务中的美中不足之处很容易引起消费者的消极情绪. 同时, 这一结论对商家也具有一定的警醒作用, 商家应该对此类评论加以重视, 根据评论内容分析对应消费者的消费心理, 扑捉到自身服务的欠缺之处, 如果能够弥补美中不足之处可能就会带来意想不到的利润.
(3) “必点”的系数在两个回归中的结果都显著为正, 体现出了消费者对某个菜品的青睐; “地道”和“川菜馆”在两个回归结果中显著为正, “辣味”也在回归一中显著为正, 体现出了餐厅的独特之处. 这些都是最能体现出一个餐厅特色的词汇, 系数显著为正的回归结果说明餐厅特色菜是影响消费者评价的一个关键因素, 说明餐饮业的商家在经营过程中要有能力打造出自己的特色, 并且注重招牌菜的推广, 这在很大程度上有利于餐厅的经营, 从而提升自身的市场竞争力.
(4) “态度”、“半天”、“电梯”以及第二个回归中“昏暗”的系数显著为负, 说明服务态度和环境的好坏直接影响了消费者的心理, 强调了餐厅服务态度和外部环境特征的重要性. 现代人的消费观念不断转换, 对服务的要求也随之提高, 更是体现在方方面面. 好的服务态度和就餐环境给消费者更加舒适、放松的感觉, 直接影响消费者的情绪, 对消费者的评分起到重要作用.
(5) “下次”、“值得”和“每次”的回归系数显著为正, 体现出了顾客再次消费的潜质, 说明这类消费者对消费行为的整体评价较高, 再次消费的可能性很大. 商家为提高顾客忠诚度、改善经营状况, 要时常关注这类消费者的消费动向, 注意维护此类消费者的顾客忠诚度.
5 结论及启示本文将Lasso算法运用到网络评论的文本分析中, 首先建立了Lasso-Logistic和Lasso-PCA两个模型对消费者情感极性进行预测. 由分析结果可知, 两种预测模型都取得了一定的预测效果. 根据100次随机抽样结果, Lasso-PCA预测模型的AUC平均值达到0.67, 而Lasso-Logistic预测模型的AUC平均值为0.64. 相比之下, Lasso-PCA模型整合了更多的变量信息, 对文本的情感极性具有更好的预测效果; 但是Lasso-PCA模型对变量的解释能力较弱, 尤其在解释变量维度较高的情况下, Lasso-PCA模型很难分析出解释变量对被解释变量的影响. 因此, 文中第4节借助Lasso-Logistic模型分析了影响消费者情感极性的显著性因素作为补充分析. 结果表明, 餐厅特色、餐厅的服务态度和外部环境等是影响消费者情感极性的主要因素. 另外, “中规中矩”和“还算”两个特征项的系数显著为负也反映了消费者对消费行为的高标准、高期望, 即使在市场逐渐细分的大环境下, 商家要想维护顾客忠诚度以长期生存下去, 也必须根据市场要求不断完善自己.
| [1] |
李胜宇, 高俊波, 许莉莉. 面向酒店评论的情感分析模型. 计算机系统应用, 2017, 26(1): 227-231. DOI:10.15888/j.cnki.csa.005511 |
| [2] |
Clavel C, Callejas Z. Sentiment analysis: From opinion mining to human-agent interaction. IEEE Transactions on Affective Computing, 2016, 7(1): 74-93. DOI:10.1109/TAFFC.2015.2444846 |
| [3] |
Zheng LJ, Wang HW. Sentimental polarity and strength of online cellphone reviews based on sentiment ontology. Journal of Industrial Engineering and Engineering Management, 2017, 31(2): 47-54. |
| [4] |
曾津, 周建军. 高维数据变量选择方法综述. 数理统计与管理, 2017, 36(4): 678-692. |
| [5] |
Weiser M. The computer for the 21st century. IEEE Pervasive Computing, 2002, 1(1): 19-25. DOI:10.1109/MPRV.2002.993141 |
| [6] |
Aizawa A. An information-theoretic perspective of TF-IDF measures. Information Processing & Management, 2003, 39(1): 45-65. |
| [7] |
Turney PD. Thumbs up or thumbs down?: Semantic orientation applied to unsupervised classification of reviews. Proceedings of the 40th Annual Meeting on Association for Computational Linguistics. Philadelphia, PA, USA. 2002. 417–424.
|
| [8] |
Hu M, Liu B. Mining and summarizing customer reviews. Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Seattle, WA, USA. 2004. 168–177.
|
| [9] |
覃世安, 李法运. 文本分类中TF-IDF方法的改进研究. 现代图书情报技术, 2013(10): 27-30. DOI:10.11925/infotech.1003-3513.2013.10.05 |
| [10] |
Mascolo C, Capra L, Zachariadis S, et al. XMIDDLE: A data-sharing middleware for mobile computing. Wireless Personal Communications, 2002, 21(1): 77-103. DOI:10.1023/A:1015584805733 |
| [11] |
Sebastiani F. Machine learning in automated text categorization. ACM Computing Surveys, 2002, 34(1): 1-47. DOI:10.1145/505282.505283 |
| [12] |
Pang B, Lee L, Vaithyanathan S. Thumbs up? Sentiment classification using machine learning techniques. Proceedings of EMNLP. Philadelphia, PA, USA. 2002. 79–86.
|
| [13] |
王健, 张俊妮. 统计模型在中文文本挖掘中的应用. 数理统计与管理, 2017, 36(4): 609-619. |
| [14] |
Geladi P, Kowalski BR. Partial least-squares regression: A tutorial. Analytica Chimica Acta, 1986, 185: 1-17. DOI:10.1016/0003-2670(86)80028-9 |
| [15] |
曹芳, 朱永忠. 基于多重共线性的Lasso方法. 江南大学学报(自然科学版), 2012, 11(1): 87-90. |
| [16] |
方匡南, 章贵军, 张惠颖. 基于Lasso-Logistic模型的个人信用风险预警方法. 数量经济技术经济研究, 2014, 31(2): 125-136. |
| [17] |
倪新洁, 梁彪, 倪佩可. 结合LASSO算法与logistic回归模型的P2P信贷审批结果研究. 统计与管理, 2015(8): 44-47. |
| [18] |
吴方照, 王丙坤, 黄永峰. 基于文本和社交语境的微博数据情感分类. 清华大学学报(自然科学版), 2014, 54(10): 1373-1376, 1383. |
| [19] |
郑文斌. 基于正则化线性统计模型的文本分类研究[博士学位论文]. 杭州: 浙江大学, 2012.
|
| [20] |
Zou H, Hastie T, Tibshirani R. Sparse principal component analysis. Journal of Computational and Graphical Statistics, 2006, 15(2): 265-286. DOI:10.1198/106186006X113430 |
| [21] |
Jolliffe IT. A note on the use of principal components in regression. Applied Statistics, 1982, 31(3): 300-303. DOI:10.2307/2348005 |
| [22] |
Witten DM, Tibshirani R, Hastie T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics, 2009, 10(3): 515-534. DOI:10.1093/biostatistics/kxp008 |
| [23] |
胡局新, 张功杰. 基于K折交叉验证的选择性集成分类算法. 科技通报, 2013, 29(12): 115-117. DOI:10.3969/j.issn.1001-7119.2013.12.039 |
| [24] |
王运生, 谢丙炎, 万方浩, 等. ROC曲线分析在评价入侵物种分布模型中的应用. 生物多样性, 2007, 15(4): 365-372. |
| [25] |
邹洪侠, 秦锋, 程泽凯, 等. 二类分类器的ROC曲线生成算法. 计算机技术与发展, 2009, 19(6): 109-112. |
 2018, Vol. 27
2018, Vol. 27



