2. 中国科学院 沈阳计算技术研究所, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China
Spark是起源于美国加州大学伯克利分校AMPLab的大数据计算平台, 它提出的弹性分布式数据集(Resilient Distributed Dataset, RDD)概念能够在分布式内存中快速处理大数据, 因此Spark 在内存处理速度上比Hadoop MapReduce要高100倍, 除此之外Spark的功能涵盖了数据的离线批处理和实时流数据处理, 机器学习, 图计算和SQL数据处理等各种类型的操作[1]. 这一系列因素使得Spark在大数据领域被越来越广泛的使用. 在实际使用中通常需要根据需求优化Spark平台, 但是因为Spark的底层运行机制对用户来讲是透明的, 所以如何合理分配集群资源和优化Spark作业性能就成为一个值得研究的问题. 性能预测是集群资源分配优化模型的基础和核心, 本文正是基于此提出了一种基于关键阶段分析的Spark性能预测模型. 通过对Spark作业运行性能进行预测从而合理分配集群资源提高作业运行效率.
2 相关工作近几年, 随着各种大数据计算平台的流行, 为了高效的管理和利用集群资源, 很多学者提出了一些性能预测模型和方案. 文献[2–8]只是部分针对Hadoop平台的性能预测研究.
目前针对Spark平台的性能预测研究还比较少. Wang KW等[9]提出了理论分析模拟Spark作业的方法预测其性能(运行时间和内存使用等), 能够获得较好的准确度, 但是需要对作业进行详细的分析. Wang GL等[10] 提出了使用机器学习的方式预测作业在不同参数下的性能表现, 对比了决策树、线性回归、支持向量机和神经网络方法在预测Spark性能方面的准确度, 但是该方法完全采用黑盒方法, 没有结合Spark作业的运行特征, 对不同类型的作业性能预测缺少支持. 陈侨安等[11]提出的基于近邻搜索算法的 Spark 参数自动优化, 主要思路是通过提取 Spark作业的特征, 比如运行日志和DAG图等, 然后在历史数据库中查询相似作业, 并把相似作业执行效率最高的配置参数作为当前作业的最优配置参数, 这种方法有几个缺陷, 第一是通过图的编辑距离来判断DAG图的相似性, 计算性较大且图的编辑距离方法本身已经被证明为是一个NP难问题; 第二是该方法的相似性判断不一定能够选取出相似作业.
本文在借鉴前人工作的基础上, 通过分析大量的Spark作业运行特征, 提出了Spark作业关键阶段的概念, 并基于此建立了一种Spark性能预测模型. 本文组织结构如下: 第3节阐述Spark原理, 提出关键阶段的概念, 并对关键阶段和Spark性能之间的关系进行分析; 第4节介绍通过关键阶段建立Spark性能预测模型; 第5节通过实验验证该模型, 证明该模型能够得到较好的预测效果.
3 关键阶段分析 3.1 Spark作业运行时间分析用户提交的程序被Spark分解成n个作业(job), 每个作业又被分解为m个阶段(stage), 各个阶段之间串行执行. 每个阶段中包含若干任务(task). 为了能够并行进行计算, 每个阶段中的一批任务并行处理其中的可容错弹性分布数据集(RDD). 因此我们可以将Spark应用的执行时间定义为如下公式:
| ${T_{\rm{application}}} = {T_{\rm{start}}} + \sum\limits_{i = 0}^n {T{}_{{{\rm{job}}_i}} + {T_{\rm{end}}}} $ | (1) |
| ${T_{\rm{job}}} = \sum\limits_{j = 0}^m {{T_{{{\rm{stage}}_j}}}} $ | (2) |
其中,
因为每个阶段内部的任务是按照批次进行的, 同一批次内部并行执行, 并行执行受到集群的资源分配(机器核数,executor个数等)和作业类型等多个因素的影响, 所以不能按照简单批次时间累加. 如果去分析所有的任务的执行时间会消耗大量的计算成本和时间成本. 我们经过大量的实验发现, 在Spark作业的每个阶段在不同输入数据量的情况下对作业执行时间产生影响不同, 如图1所示. 我们可以发现一个共同特点:有的阶段运行时间在不同的输入数据量下基本保持不变, 有的则会产生较大变化从而影响整个作业的运行时间, 还有的阶段对应的运行时间为0, 这是因为该阶段的计算结果因为缓存到了内存之中, 在后续需要使用该结果的时候可以直接取出从而不再需要计算. 以图1(a)中的WordCount程序为例, 我们可以看出Stage0阶段的运行时间在整个作业运行中的时间比重较大, 而且随着数据量的变化产生明显的变化. Stage1所占比例较小, 且基本稳定. 我们通过实验分析其他几种类型的作业, 比如Sort, PageRank和K-Means, 均有相似性质, 因此我们提出了关键阶段的概念.
定义1. 关键阶段. 对于一个Spark作业其关键阶段需要同时满足以下条件:
(1) 该阶段的运行时间大于整个作业运行时间的均值
(2) 该阶段的运行时间随输入数据量的变化而变化的幅度大于该作业每个阶段运行时间变化幅度的均值

|
图 1 几种常见Spark程序处理在不同输入数据量时的各个阶段运行时间 |
3.3 关键阶段和Spark性能之间的关系
本文我们选取Spark作业的运行时间作为Spark性能的衡量指标, 因此本文的目的即预测在不同的输入数据量的情况下Spark作业的运行时间. 为了建立该模型, 我们需要分析关键阶段的运行时间和和Spark作业不同输入数据量之间的关系.
以WordCount程序为例, 我们通过实验得出关键阶段的运行时间在不同输入数据量情况下的关系图, 如图2所示.
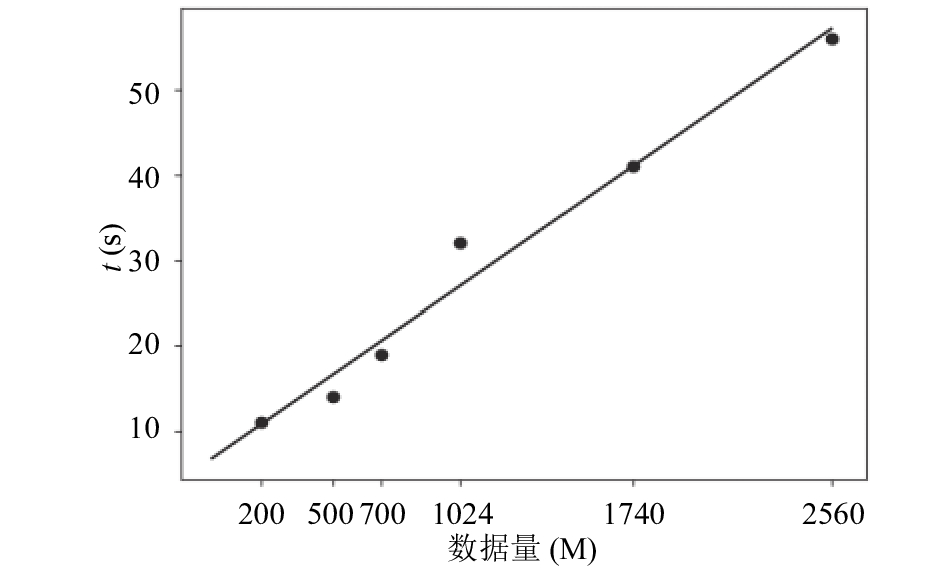
|
图 2 关键阶段运行时间和不同输入数据量关系图 |
在图中我们可以看出在WordCount程序中关键阶段的运行时间和数据量之间可以拟合成一种线性回归关系, 即
| $T_{\rm{stage}}^{key} = \alpha {D_{\rm{input}}} + \beta $ | (3) |
虽然不同类型的Spark 作业的资源消耗情况等各种运行情况不尽相同, 比如 CPU 密集型作业和I/O密集型作业需要的集群资源不同, 但是我们通过实验发现多数作业的关键阶段运行时间和数据量之间的关系具有回归关系. 所以公式(3)可以表达为以下公式:
| $T_{\rm{stage}}^{key} = f({D_{\rm{input}}})$ | (4) |
通过上述两节的分析以及公式(2), 我们定义对Spark作业执行时间的预测公式:
| $T_{\rm{job}}^p = \sum\limits_{i = 0}^m {T_{{\rm{stage}}{_i}}^{key} + \sum\limits_{j = 0}^n {T_{{\rm{stage}}{_j}}^r} } $ | (5) |
| $T_{\rm{stage}}^r = \frac{{\sum\limits_{i = 0}^N {T_{{\rm{stage}}{_i}}^r} }}{N}$ | (6) |
其中, Tkeystage表示关键阶段的运行时间, Trstage表示其它阶段的时间, 这些阶段的运行时间在不同输入数据量的情况下基本可以认为保持不变.
具体建模步骤:
(1) 运行小批量不同大小的数据集, 收集作业的运行信息: 阶段个数, 每个阶段的起止时间等.
(2) 根据算法1求出关键阶段.
算法1. 求解关键阶段
输入: 步骤1获取的运行信息.
输出: 关键阶段相关信息.
① 根据每个阶段的起止时间计算每个阶段的运行时间和整个作业的运行时间均值Tmean.
② 依次判断每个阶段的运行时间是否大于Tmean, 并将大于均值的编号存储到List1.
③ 遍历List1中的编号, 获取对应的每个阶段运行时间的变化幅度和求出总的变化幅度的均值Dmean.
④ 返回List1中大于Dmean的阶段即为所求.
(3) 根据步骤(1)的信息结合有关机器学习回归算法获取公式(4)的具体表达式.
(4) 根据公式(5)(6)获取作业的预测运行时间.
5 实验验证本文所使用的实验环境的是三个节点组成的Spark分布式集群, 集群采用主从架构, 其中的一个节点是主节点, 另外两台为从节点. 节点的操作系统是CentOS Linux release 7.2.1511 64 bit, 内存为8 G, 处理器4核4线程; 使用的Spark版本是2.0.1, Hadoop版本为2.7.3, 并且使用Hadoop 的YARN作为分布式集群的资源调度器; java版本是1.8.0_131; 基准测试程序BigDataBench[12]. 实验中我们分别针对WordCount, PageRank和K-Means程序进行作业性能预测. 首先使用小数据量数据集得出公式(4)的表达式, 然后根据该公式预测大数据量情况下作业的运行时间.
针对WordCount和K-Means程序, 采用的训练数据量是100 M~1.5 G, 间隔200 M, 预测5 G数据量下运行时间; 针对PageRank程序, 采用的训练数据图为节点1024到32 768, 边数为2147到99 489, 预测节点数为3 048 576, 边数为4 610 034图的处理时间. 得到结果如图3.
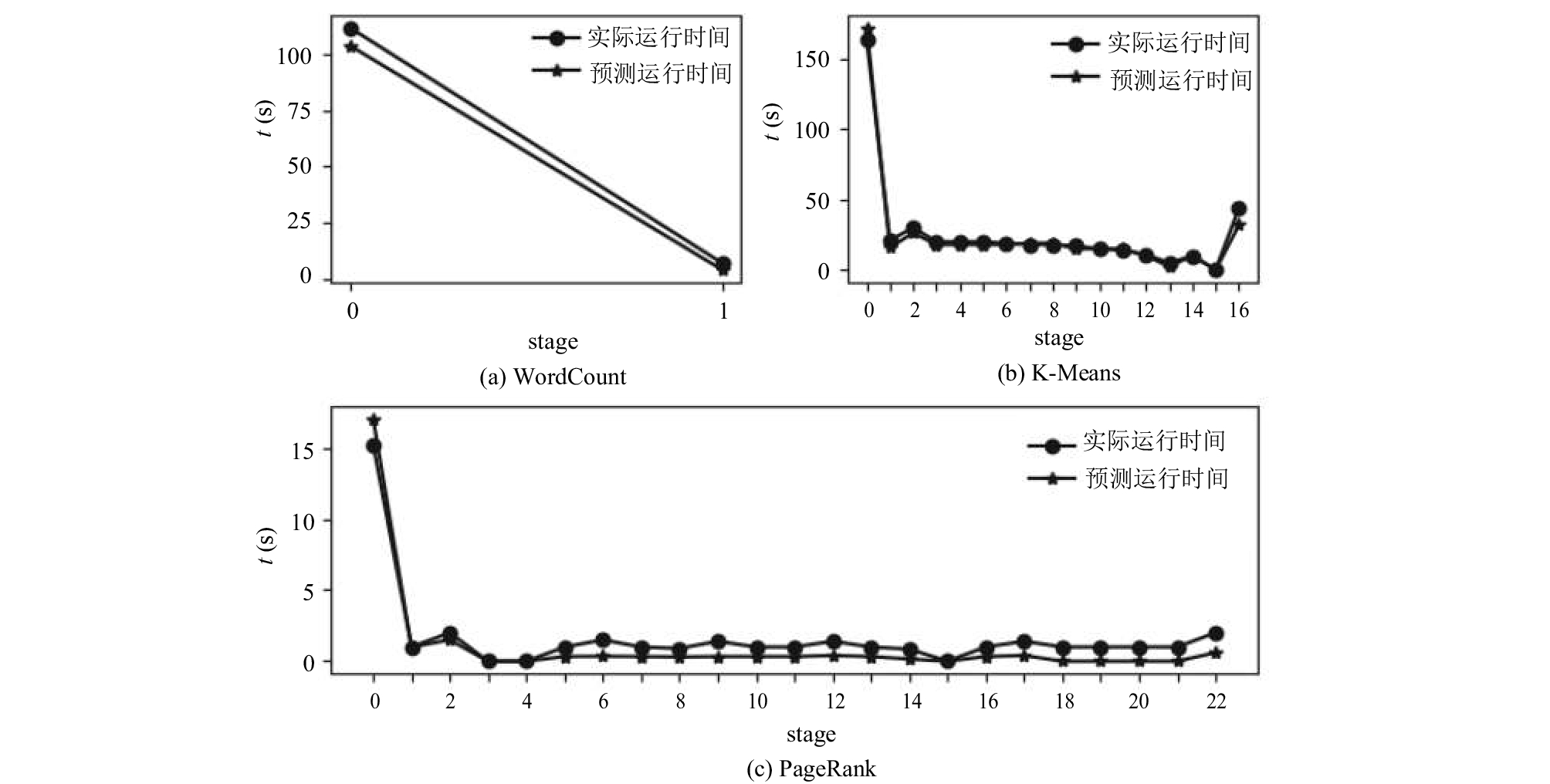
|
图 3 几种常见Spark程序在该模型下预测各阶段运行时间和实际运行时间的对比 |
如图3, 实验结果显示预测模型能够整体上反映Spark作业的运行态势, 而且可以较为准确的预测出Spark作业的运行时间. 同时分析图3(c)中的PageRank预测结果可以发现后面有几个阶段(18, 19, 20)的预测运行时间均为0, 这是因为实验中运行的小批量训练数据集和验证运行的大数据集的阶段个数不一致导致的. 因为这些阶段不是关键阶段, 也就是在整个作业运行时间中占有极小的一部分比例, 所以对整体运行时间的预测结果影响不大. 将实验结果和文献9的结果相对比发现两者所预测的作业执行时间准确度相似, 但是本文所使用的方法不需要人工对作业进行详细的分析从而能具有更好的效率.
6 总结本文首先通过实验分析Spark作业的不同阶段运行时间在整个作业运行时间所占比重的不同, 提出了Spark作业的关键阶段这个概念, 然后通过分析Spark作业输入数据量和关键阶段运行时间之间的关系提出了一种基于关键阶段分析的Spark性能预测模型, 并且通过实验验证该模型预测结果较为有效. 除此之外, 关键阶段分析对Spark平台的其它资源消耗预测(比如CPU和内存等)具有参考意义.
| [1] |
Apache Spark. http://spark.apache.org/.
|
| [2] |
Rizvandi NB, Taheri J, Moraveji R, et al. On modelling and prediction of total CPU usage for applications in mapreduce environments. Proceedings of the 12th International Conference on Algorithms and Architectures for Parallel Processing. Fukuoka, Japan. 2012. 414–427.
|
| [3] |
李振举, 李学军, 刘涛, 等. MapReduce性能预测模型构建. 计算机技术与发展, 2016, 26(1): 70-73. |
| [4] |
Khan M, Jin Y, Li MZ, et al. Hadoop performance modeling for Job estimation and resource provisioning. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(2): 441-454. DOI:10.1109/TPDS.2015.2405552 |
| [5] |
周世龙, 陈兴蜀, 罗永刚. 基于灰盒模型的Hadoop MapReduce job参数性能分析与预测. 四川大学学报(工程科学版), 2014, 46(Z1): 146-154. |
| [6] |
Kavulya S, Tan JQ, Gandhi R, et al. An analysis of traces from a production MapReduce cluster. Proceedings of the 2010 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing. Melbourne, VIC, Australia. 2010. 94–103.
|
| [7] |
Yang HL, Luan ZZ, Li WJ, et al. MapReduce workload modeling with statistical approach. Journal of Grid Computing, 2012, 10(2): 279-310. DOI:10.1007/s10723-011-9201-4 |
| [8] |
Popescu AD, Balmin A, Ercegovac V, et al. PREDIcT: Towards predicting the runtime of large scale iterative analytics. Proceedings of the VLDB Endowment, 2013, 6(14): 1678-1689. DOI:10.14778/2556549 |
| [9] |
Wang KW, Khan MMH. Performance prediction for apache spark platform. Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, 2015 IEEE 12th International Conference on Embedded Software and Systems. New York, NY, USA. 2015. 166–173.
|
| [10] |
Wang GL, Xu JG, He B. A novel method for tuning configuration parameters of spark based on machine learning. Proceedings of the 2016 IEEE 18th International Conference on High Performance Computing and Communications, IEEE 14th International Conference on Smart City; IEEE 2nd International Conference on Data Science and Systems. Sydney, NSW, Australia. 2016. 586–593.
|
| [11] |
陈侨安, 李峰, 曹越, 等. 基于运行数据分析的Spark任务参数优化. 计算机工程与科学, 2016, 38(1): 11-19. DOI:10.3969/j.issn.1007-130X.2016.01.002 |
| [12] |
詹剑锋, 高婉铃, 王磊, 等. BigDataBench: 开源的大数据系统评测基准. 计算机学报, 2016, 39(1): 196-211. DOI:10.11897/SP.J.1016.2016.00196 |
 2018, Vol. 27
2018, Vol. 27


