多旅行问题(Multiple Traveling Salesmen Problem, MTSP)是TSP的扩展. 给定一个中心城市和n个访问城市, 将访问城市分配给m个旅行商, 每个旅行商从中心城市出发巡游若干访问城市后回到中心城市, 要求所有旅行商经过的总路程(total)尽量小且其中最长环路的长度(max)尽量小. 事实上, 无法保证total和max两个目标同时达到最小, 本文寻求最小化max, 称之为MinMax-MTSP. 这一类问题的算法可应用在工作均衡调度, 印刷机调度、卫星测量系统设计、机器人应急响应[1–3]等领域.
城市集合C={c0,c1,c2,…,cn}, c0表示中心城市, c1, c2,…,cn表示访问城市. 距离矩阵D={di,j}, di,j为ci到cj的距离. 每条环路用城市号序列来编码, 例如cycle = (0,1,2)表示c0→c1→c2→c0. 图1显示了n=10, m=3的MinMax-MTSP的一个解(非最优解), 其中的3条环路分别是(0,1,2), (0,5,4,3)和(0,6,7,8,9,10), 解表示为S=(0,1,2,0,5,3,4,0,6,7,8,9,10). MinMax-MTSP求解目标是寻找S的最佳序, 使max最小.
将进化算法与局部搜索算法结合来求解MTSP是近年来的主要方法. 一类是遗传算法, Carter[4]提出了一种双基因编码(城市基因和组基因)的遗传算法, 并提出了12个测试例; Brown[5]提出一种分组遗传算法. Yuan[6]在分组遗传算法中引入了一种新的交叉算子(TCX), 提出了3个新的测试例; Singh[7]改进了分组遗传算法(GGA-SS), 用组的rk值(rk=路径长度/城市数)衡量一个组属于最优解的可能性, rk值较大的组优先保留在子代中, 其余一些零散的城市用贪心算法插入到各个组, 使用2-opt局部搜索算子进行组内优化. 另一类是群体智能算法, Liu[8]用蚁群算法求解MTSP; VENKATESH[9]提出了两种蜂群算法(ABCFC、ABCVC) 和一种杂草入侵算法 (IWO), 同样用2-opt进行组内优化.

|
图 1 3个旅行商10个访问城市的一个解 |
以上算法的一致性在于: 使用局部搜索算法来快速加速寻优过程, 使用群体进化算法不断累计优化结果. 这些算法采用2-opt作为局部搜索算子, 而且仅将2-opt作用于单条环路的优化. 实际上, 在MTSP中, 可以将局部搜索从单条环路的优化扩展为两条环路的重组优化, 加速算法的寻优过程(第2节讨论). 这些算法主要依赖个体之间交换信息来完成迭代优化, 很少考虑到局部搜索算子自身的特点, 在进化算法中根据局部搜索算子自身的特点, 设计新的进化机制, 是本文关注的另一个重要内容(在第3节讨论).
本文设计了一个新的局部搜索算子reverse/ move (转置/移动), 该算子既能进行一条环路的优化, 也能重组优化两条环路, 即便在一条环路上进行优化, 其能力也明显好于2-opt; 在分析reverse/move算子特点的基础上, 提出了“搜索-选优-变异-搜索”策略, 设计了竞争搜索算法(Competitive Search Algorithm, CSA), 在文献[4]和文献[6]的15个测试例上进行实验, 与文献[6–9]进行比较, CSA在计算结果上有明显的改进.
2 局部搜索算子reverse/move为了指导搜索过程, 需要对解有合适的评价方法. MinMax-MTSP的目标是最小化max, 但注意到, 将目标改为优先最小化max, 其次最小化total, 有助于最小化max. 因为后者要求每一条环路自身次序最优, 在大多数情况下, 这有利于最小化max.
以图1为例, 算法运行到当前步骤, (0,6,7,8, 9,10)是最长环路, 次序已经是最优; (0,5,3,4)是另外一条稍短的环路, 次序不是最优. 此时对(0,5,3,4)进行优化得到(0,3,4,5), 然后从(0,6,7,8,9,10)中移动“6”到(0,3,4,5)可以得到(0,3,4,5,6), 这是一条新的最长环路, 而且比前一条最长环路更短.
因此, 将解的适应值设计为一个二元组(max, total), 规定: 解S1优于解S2, 当且仅当(max1<max2) 或 (max1=max2且total1<total2).
本文局部搜索算子通过依次检查S中的每一个位置来完成. 下文中, 将被检查位置上的城市标记为c1, 它在S中的后一个城市标记为c3, c1的邻域N(c1)中的城市的标记为c2, c4和c5分别是c2在S中的后一个城市和前一个城市. 按照Lin-kernighan算法的建议, N(c1)取离c1最近的6个城市.
我们的局部搜索方法是: 依次检查S的每一个位置, 对于该位置上的城市c1, 对N(c1)中每一个c2, 做两种尝试: 先尝试转置c2与c3之间(包含c2与c3)的次序, 得到S', 如果S'优于S, 则用S'代替S; 否则尝试将c2移动到c1和c3之间, 得到S', 如果S'优于S, 则用S'代替S. S包含n+m个位置, 如果连续检查n+m个位置都无法优化S, 算子停止. 转置和移动合称“reverse/move”.
c2和c3可能位于S中的同一环路, 也可能位于两条不同的环路, 以下分别进行讨论.
当c2和c3在同一环路中, 转置c2和c3之间的次序将删除两条边并新增两条边, 效果如图2(a), 例如: cycle=(0,1,2,3,4,5,6), c2=1, c3=5, reverse (cycle)=(0,5,4,3,2,1,6); 移动c2将删除三条边并新增三条边, 效果如图2(b), 例如: cycle=(0,1,2,3,4,5,6), c2=1, c3=5, move(cycle)=(0,2,3,4,1,5,6).
当c2和c3属于分属两条环路. 转置c2和c3之间的次序, 将对两条环路进行重组, 效果如图3(a), 例如: S=(0,1,2,0,5,3,4,0,6,7,8,9,10), c2=1, c3=7, reverse(S)=(0,7,6,0,4,3,5,0,2,1,8,9,10). 移动c2, 相当于将c2从一条环路中移除, 插入到另一条环路, 效果如图3(b), 例如: S=(0,1,2,0,5,3,4,0,6,7,8,9,10), c2=1, c3=7, move(s)=(0,2,0,5,3,4,0,6,1,7,8,9,10).

|
图 2 一条环路中的转置/移动 |

|
图 3 跨两条环路的转置/移动 |
我们在经典TSP的公开测试数据TSPLIB上比较reverse/move与2-opt. 经典TSP问题相当于m=1的MTSP问题, 其上的测试结果能够反映局部搜索算子的寻优能力. 对每个测试例, 分别产生800个随机的初始解, 然后各用reverse/move与2-opt两种局部搜索进行优化, 得到800个最终解. 从两个方面进行比较: 1) 环路长度(length)的平均值, 2) 检查位置数(checked-points)的平均值, 结果如表1.
| 表 1 reverse/move与2-opt的搜索能力比较 |
表1显示, 对每一个测试例, 两种局部搜索算法在停止时, reverse/move检查的位置数略大于2-opt, 与此同时, 在搜索的结果上, reverse/move的明显好于2-opt.
3 竞争搜索算法当reverse/move算子停止搜索时, 对所得到的解S, 选择其中一个片段, 转置其次序, 然后再执行reverse/move, 可能得到更优的解. 以图4为例, 图4(a)是reverse/move得到的一个解, 图4(b)是一次转置的结果, 图4(c)和图4(d)是再次执行reverse/move的中间过程和结果.

|
图 4 转置一个片段后再次执行reverse/move |
用一对城市号(cstart, cend)来标记S中的一个片段, 这样的对共有(n+m)×(n+m-1)/2个, 构成S的候选对集. 用随机方式来选择一对城市, 转置其所标记的片段, 然后再次执行reverse/move, 可能有三种结果: 1) 得到更好的解, 2) 恢复到转置之前的解, 3) 得到变差的解. 每选出一对城市, 就从S的候选对集中将其删除, 直到候选对集为空.
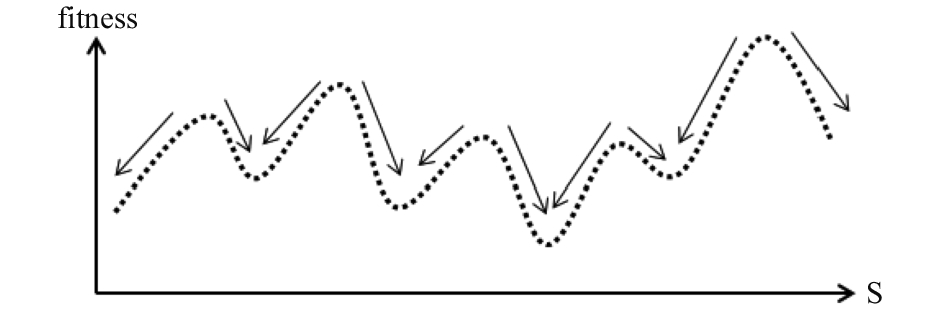
根据reverse/move的以上特点, 我们提出一种群体迭代策略: “搜索-选优-变异-搜索”, 用图5说明. 图5中的横坐标是解空间, 纵坐标是解的适应值. 如果一组解经过局部搜索得到相同的局部最优解, 则将这组解集中在一个区域, 该区域中适应值最小的解就是该区域的局部最优解. 选择最好的若干个局部最优解, 对其进行变异(随机的片段转置), 得到的一部分新的解将到达新的区域, 经再次搜索得到新的局部最优解. 如此迭代, 逐步提高局部最优解的质量, 直至最好的若干个局部最优解的候选对集全部为空.
|
图 5 多个解经过局部搜索得到相同的局部最优解 |
基于这一策略, 我们设计了竞争搜索算法(CSA), 如算法1.
CSA算法与保留精英的遗传算法相似, 其特异性在于: 用局部搜索reverse/move取代杂交操作; 用最优且互异的若干个体作为父代个体, 取代概率性选择; 用固定的小尺度变异(转置一个片段)替代概率性变异.
4 实验我们用文献[4]的12个测试例和文献[6]的3个测试例作为实验数据. 文献[4] 的12个测试例中的城市数据是二维平面坐标, 包括MTSP-51的3个问题(m=3, m=5, m=10), MTSP-100的4个问题(m=3, m=5, m=10, m=20)和MTSP-150的5个问题(m=3,m=5, m=10, m=20, m=30), 用第一个城市作为中心城市. 文献[6]的3个测试例中的数据是128个城市的经纬度和距离矩阵, 包括sgb128(m=10, m=15,m=30), 用第一个城市作为出发城市.
我们在2.8 GHz, 2 Core, 4 G RAM的Windows 8.1系统上实现了CSA, 在实验中种群规模p设置为50. 表2给出了CSA在15个测试例上得到的最小的最长环路长度(best max)、迭代次数(iterations)和计算时间(time).
| 表 2 CSA算法的结果、迭代次数和时间 |
表2说明, CSA能在较短时间内终止, 满足实际应用的需求.
对于文献[4]的12个测试例, CSA所得的best max与文献[6–9]的结果比较如表3.
| 表 3 几种算法在文献[4]测试例上的best max比较 |
由表3, 对文献[4]的12个问题, 在所有算法中, CSA的结果都优于或等于现有算法的最好结果, 其中两个测试例MTSP-150 (m=3, m=5)的解展示在图6中.

|
图 6 CSA在文献[6]问题上的两个解 |
对于文献[6]的3个测试例, CSA所得的best max与文献[6–9]的结果比较如表4.
由表4, 对文献[6]的3个测试例, CSA的结果有大幅度改进. 由于文献[6]提供的128城市的坐标用经纬度来表示, 在二维平面较难展示, 下面给出m=10, max=2748的解, 其中每一对括号包含的是一条环路.
| 表 4 几种算法在文献[6]测试例上的best max比较 |
cycle1: (0,95,65,22,81,44,78,23,61,122,101,46,82, 107,4,93)
cycle2: (0,89,127,111,74,114,126,80,8,98,7,15,14)
cycle3: (0,73,59,109,39,60,116,92,3,76,35,105,40, 66,62,17,53)
cycle4: (0,21,16,52,77,28,10,11,34,125,106, 102,30,90)
cycle5: (0,88,108,54,118,112,25,85,97,87,27, 42,86,41)
cycle6: (0,100,13,83,36,67,1,75,9)
cycle7: (0,47,70,68,120,50,99,84,31,55,63,123, 12,58,32)
cycle8: (0,57,48,49,2,56,96,117,124,113,104)
cycle9: (0,26,18,45,115,94,64,43,91,29,37)
cycle10: (0,130,71,69,79,33,72,103,51,20,110, 19,24,121,6,38,5,119)
5 结论为了求解最大最小目标的多旅行商问题, 在对现有文献进行研究的基础上, 提出了竞争搜索算法(CSA), 与近期文献中的相比, 明显提高了解的质量. 局部搜索算子和变异算子是CSA算法中的两个关键算子. 我们曾采用多种不同的变异算子, 包括: 随机移动一个城市、随机转置一个片段、随机转置两个或多个片段以及这些操作的组合, 我们观察到, 采用不同的变异算子, 在收敛速度和最终解质量上有明显差异, 其中, 随机转置一个片段的变异方法明显好于其他方法. 改进变异方法, 可能进一步提高CSA算法性能.
| [1] |
Malmborg CJ. A genetic algorithm for service level based vehicle scheduling. European Journal of Operational Research, 1996, 93(1): 121-134. DOI:10.1016/0377-2217(95)00185-9 |
| [2] |
Saleh HA, Chelouah R. The design of the global navigation satellite system surveying networks using genetic algorithms. Engineering Applications of Artificial Intelligence, 2004, 17(1): 111-122. DOI:10.1016/j.engappai.2003.11.001 |
| [3] |
Trigui S, Koubâa A, Cheikhrouhou O, et al. A clustering market-based approach for multi-robot emergency response applications. 2016 International Conference on Autonomous Robot Systems and Competitions. Braganca, Portugal, 2016, 137-143. DOI:10.1109/ICARSC.2016.14 |
| [4] |
Carter AE, Ragsdale CT. A new approach to solving the multiple traveling salesperson problem using genetic algorithms. European Journal of Operational Research, 2006, 175(1): 246-257. DOI:10.1016/j.ejor.2005.04.027 |
| [5] |
Brown EC, Ragsdale CT, Carter AE. A grouping genetic algorithm for the multiple traveling salesperson problem. International Journal of Information Technology & Decision Making, 2007, 6(2): 333-347. DOI:10.1142/S0219622007002447 |
| [6] |
Yuan S, Skinner B, Huang SD, et al. A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms. European Journal of Operational Research, 2013, 228(1): 72-82. DOI:10.1016/j.ejor.2013.01.043 |
| [7] |
Singh A, Baghel AS. A new grouping genetic algorithm approach to the multiple traveling salesperson problem. Soft Computing, 2009, 13(1): 95-101. DOI:10.1007/s00500-008-0312-1 |
| [8] |
Liu WM, Li SJ, Zhao FG, et al. An ant colony optimization algorithm for the Multiple Traveling Salesmen Problem. Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications. Xi’an, China, 2009, 1533-1537. DOI:10.1109/ICIEA.2009.5138451 |
| [9] |
Venkatesh P, Singh A. Two metaheuristic approaches for the multiple traveling salesperson problem. Applied Soft Computing, 2015(26): 74-89. DOI:10.1016/j.asoc.2014.09.029 |
 2018, Vol. 27
2018, Vol. 27



