传统的SVM算法通过分类超平面来判断样本的类别, 在解决不平衡数据的分类问题时, 分类结果会偏向于多数类样本点集合, 使得少数类样本点的分类正确率低, 而多数类分类准确率高.
当前针对不平衡数据集SVM分类的改进, 一般集中在数据清洗和算法改进两个方向上. 许多学者都提出了具有代表性的改进方法, 如对于样本的欠采样方法SMOTE[1], 过采样方法Tomek links[2]以及它们相应的改进算法[3,4], 都是通过不同方法增加少数类样本或减少多数类样本, 来达到使得不同类别中的样本数量基本相当的目的. 在算法层面上, 代价敏感学习方法[5]对不平衡数据集中少数类和多数类分别设置不同的惩罚参数, 通过调整不同类别的惩罚参数, 提高不平衡数据集的分类效果, Huang[6]改进了代价敏感学习, 通过结合极限学习机来实现动态代价敏感学习; 集成学习方法[7]提出构造不同的弱分类器, 对每个弱分类器设置一个权重并组合成一个强分类器对不平衡数据集进行分类, 在集成学习方法的基础上, Zięba M等人[8]还结合了主动学习策略对每个弱分类器的代价函数进行改进.
对样本数量的增减, 都会改变使得原始样本数据的分布, 使得分类超平面的位置产生偏差; 而设置不同类别惩罚参数的方法, 对于不同的不平衡数据集中每个类别样本数量和分布情况, 较难对惩罚参数的值进行预设. 本文提出了一个在保持原数据样本不变的情况下, 应用SMO算法解拉格朗日优化方程参数
SVM算法得到一个间隔边界
| $\begin{array}{*{20}{l}}{\min }\;{\frac{1}{2}{w^{\rm T}}w + C\sum\limits_{i = 1}^N {{\varepsilon _i}} }\\{\rm {s.t.}}\;\;{1 - {\varepsilon _i} - {y_i}(w{x_i} + b) \le 0},\;\;{}{0 \le {\varepsilon _i}}\end{array}$ | (1) |
其中,
SVM算法要找的两条间隔边界是两类别样点中所有间距最小的样本点之间的最大距离. 在不平衡数据集下生成分类超平面时, 之所以分类结果会偏向多数类样本集, 本质上是因为对所有类别的样本点都使用相同的惩罚系数
SVM算法对每个样本点加入松弛变量
在上文提到对不平衡数据集代价敏感的SVM算法中, 将惩罚参数设置为
| $\begin{array}{*{20}{l}}{\max }&{W(\alpha ) = - \frac{1}{2}(\sum\limits_{i,j = 1}^N {{\alpha _i}{y_i}{\alpha _j}{y_j}{x_i}*{x_j}} ) + \sum\limits_{i = 1}^N {{\alpha _i}} }\\{\rm {s.t.}}&{0 \le {\alpha _i} \le {C^ + }},\;{}{0 \le {\alpha _i} \le {C^ - }},\;{}{\sum\limits_{i = 1}^N {{\alpha _i}{y_i}} = 0}\end{array}$ | (2) |
用公式(2)的方式对不平衡数据集进行优化时, 在算法运行前, 要人为设置两个参数
对公式(1)求解
| $\left\{\begin{aligned}& {w = \sum\limits_{i = 1}^N {{\alpha _i}{y_i}{x_i}} }\\& {b = - \frac{{{{\max }_{i:{y_i} = - 1}}{w^{\rm T}}{x_i} + {{\min }_{i:{y_i} = 1}}{w^{\rm T}}{x_i}}}{2}}\end{aligned}\right.$ | (3) |
上式中的
在求得
下面用一个例子说明参数
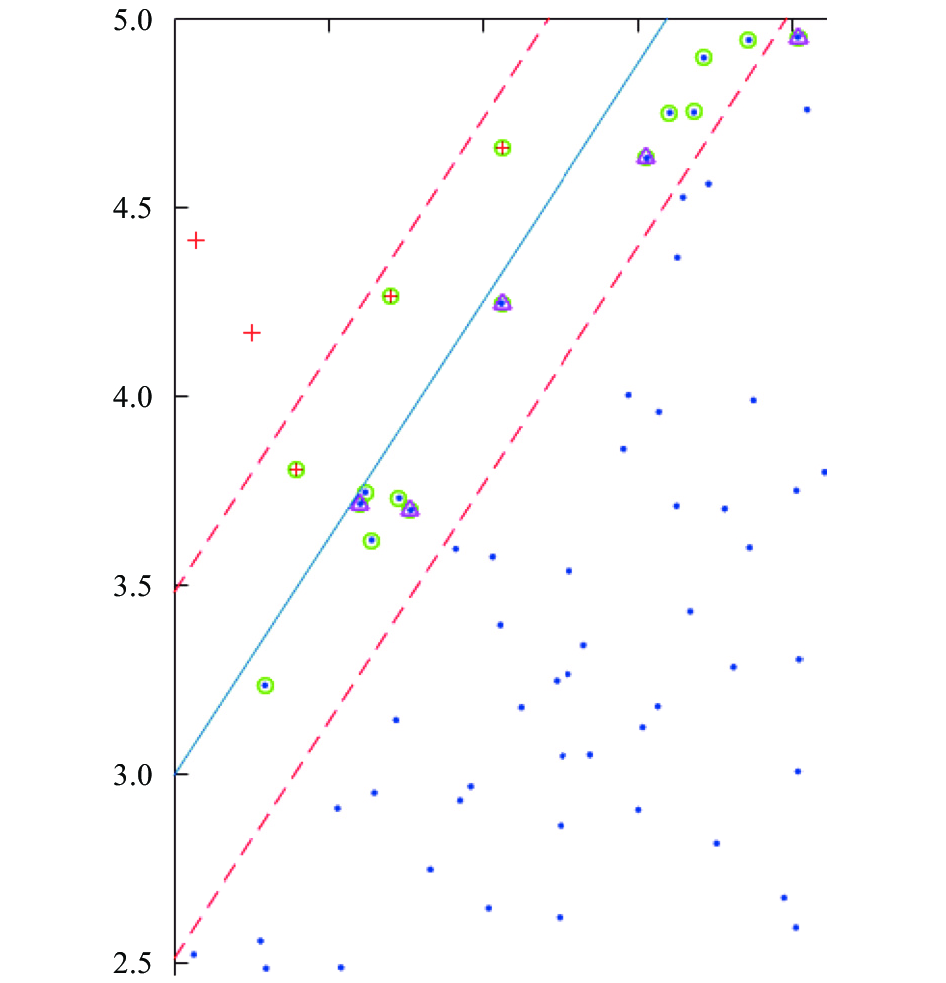
|
图 1 不平衡数据集分类结果局部放大 |
SVM分类最终得到的结果是一个分类超平面
对于图1中的不平衡数据集而言, 生成的分类超平面如果能向多数类方向移动, 即图1中实线向下移动, 在本例中相当于减小
本节提出一种直接在SMO算法求解
具体的优化算法步骤如下:
Step1. 对所有的乘子
Step2. 在除
Step3. 计算更新了
| $Ac{c^ + } = \frac{{TP}}{{NUM\_P}},\;Ac{c^ - } = \frac{{TN}}{{NUM\_N}}$ | (4) |
其中,
| $\begin{array}{*{20}{c}}{\chi = \log \left((sup\_pos + sup\_neg) \cdot \frac{{NUM\_N}}{{NUM\_P}}\right)}\\{C\_b = \frac{{Ac{c^ - }}}{{Ac{c^ + }}} \cdot \chi }\end{array}$ | (5) |
Step4. 在对
Step5. 如果达不到迭代次数, 或者更新的过程中
Step3中的中
在SMO算法的求解过程中, 迭代更新后, 会使得求得的分类超平面向多数类方向移动, 对不平衡数据集问题, 会使得少数类的分类正确率提高, F1-Measure指标得到改善, 并且由于仅在迭代过程中增加了若干条计算语句和一个分析是否为少数类样本的判断语句, 算法的时间复杂度没有发生变化.
4 实验与结果分析下面设置了两组数据在Matlab 2016a中来验证本文算法(以下用SVM_Improved表示), 一组数据为上文中的人工数据集, 另一组为UCI[10]公共数据集中的6个不平衡数据集; 实验环境的计算机配置为: CPU为core i5, 内存4 G, 操作系统为Windows10.
4.1 人工数据集图2和本文第2节中的图1分别是采用传统SVM和SVM_Improved得到的分类超平面, 惩罚系数

|
图 2 本文算法生成的分类超平面放大图 |
第2节图1中的少数类分类正确率为50%, 多数类正确率为100%, 即少数类分对5个, 分错5个; 多数类分对210个, 没有错分样本点; 支持向量一共16个, 支持向量中少数类和多数类各一半, 少数类的F1-Measure为0.67. 图2中的少数类正确率为90%, 多数类正确率为97.14%, 少数类分对9个, 分错1个, 多数类分对204个, 分错6个. 支持向量的情况和图1中相同, 而少数类F1-Measure为0.93. 图1中的分类超平面方程为:
从UCI中抽取6个不同的不平衡数据集, 分别为heart disease, balance scale, yeast, abalone, haberman, ecoli. 如表1所示.
| 表 1 UCI不平衡数据集 |
在这6个UCI数据中, 不平衡数据集里有多个类别的, 将其中的一个或若干个类别合并设置为少数类, 即表1中为目标类别列, 而将其余类别的样本合并设置为多数类. 如数据集yeast中, 将类别标签为ME1, ME2和ME3这三个类别的44,51,163个样本合并成少数类, 而将剩余的标签为CYT等7个类别共1226个样本组成多数类. 每个数据集少数类和多数类样本数的对比为表1中的最后一列. 这四个数据集中, heart disease选择的是Cleveland数据库; abalone数据集的多数类与少数类样本数相差最大, 达到129倍, 其它五个数据集的多数类与少数类样本数相差5至15倍之间.
对这6个数据集的实验结果如表2所示, 其中Pr、Re和F1_M分别表示Precision(查准率), Recall(召回率)和F1-Measure. 算法SVM_1为对少数类和多数类分别设置不同的惩罚参数的代价敏感学习方法. 在实验中, 惩罚参数
从表2的数据中可以看出: 对于两个类别样本数量不同的多个不平衡数据集中, SVM_Improved算法的少数类样本F1_measure的值都有不同程度的提升. 特别地对于haberman数据集, 由于属性数只有4个, 并且这些属性值为整数又较接近, 即两类样本点在分类超平面附近有较多的分布, 本文算法对于少数类的分类正确的样本数较SVM_1算法多了11, 虽然此时的多数类样本点的分类正确的数量有一定的下降, 但是最后少数类F1_measure的值提升较大; 对于ecoli数据集, 样本属性值的特点和haberman数据集类似, 属性数增加到8个, 少数类分类正确的样本较SVM_1增加了13%左右, 和haberman数据集的结果接近.
| 表 2 实验结果对比(单位: %) |
对于abalone数据集, 样本相差129倍时, TP增加从17个样本增加到25个样本, 少数类分类正确的数量提高的同时多数类识别错误的样本数也较SVM算法增加了12个样本, F1-Measure的值增加了近5%, 该数据集的F1-Measure指标的提升也与haberman, ecoli这样的数据集接近. heart-disease, balance scale, yeast三个数集的TP分别较SVM算法增加了2,4,7个样本, 即少数类样本分类正确数量增加了2%至5%, 多数类正确率基本不变.
这是由于在分类超平面参数
本文提出一种改进不平衡数据集少数类样本分类精确度的SVM_Improved方法, 在求解
| [1] |
Chawla NV, Bowyer KW, Hall LO, et al. SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357. |
| [2] |
Kubat M, Matwin S. Addressing the curse of imbalanced training sets: One-sided selection. Proceedings of the Fourteenth International Conference on Machine Learning. Nashville, TN, USA. 1997. 179–186.
|
| [3] |
刘胥影, 吴建鑫, 周志华. 一种基于级联模型的类别不平衡数据分类方法. 南京大学学报(自然科学), 2006, 42(2): 148-155. |
| [4] |
Wang KJ, Adrian AM, Chen KH, et al. A hybrid classifier combining Borderline-SMOTE with AIRS algorithm for estimating brain metastasis from lung cancer: A case study in Taiwan. Computer Methods and Programs in Biomedicine, 2015, 119(2): 63-76. DOI:10.1016/j.cmpb.2015.03.003 |
| [5] |
Veropoulos K, Campbell C, Cristianini N. Controlling the sensitivity of support vector machines. Proceedings of the International Joint Conference on Artificial Intelligence. Stockholm, Sweden. 1999. 55–60.
|
| [6] |
Huang YW. Dynamic cost-sensitive ensemble classification based on extreme learning machine for mining imbalanced massive data streams. International Journal of u- and e- Service, Science and Technology, 2015, 8(1): 333-346. DOI:10.14257/ijunesst |
| [7] |
Schapire RE. A brief introduction to boosting. Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence. Stockholm, Sweden. 1999. 1401–1406.
|
| [8] |
Zięba M, Tomczak JM. Boosted SVM with active learning strategy for imbalanced data. Soft Computing, 2015, 19(12): 3357-3368. DOI:10.1007/s00500-014-1407-5 |
| [9] |
吴敏. 支持向量机分类算法的若干研究[硕士学位论文]. 南京: 南京邮电大学, 2014.
|
| [10] |
UCI. Welcome to the UC Irvine Machine Learning Repository! http://archive.ics.uci.edu/ml.
|
 2018, Vol. 27
2018, Vol. 27



