2. 西安电子科技大学 计算机学院, 西安 710071
2. School of Computer Science and Technology, Xidian University, Xi’an 710071, China
随着智能终端的普及使得视频应用越来越多样化, 涉及的视频内容丰富多样, 人们对视频分辨率的要求也随之水涨船高[1], 对视频编码压缩和传输提出更高的要求. 2013年JCT-VC (Joint Collaborative Team on Video Coding)正式发布了新一代高效视频编码标准 (High Efficiency Video Coding, HEVC)标准[2], 又称H.265, 由于新标准HEVC采用了灵活的四叉树自适应存储结构、35种的帧内预测(包括planner 模式和 DC 模式)模式、包括运动信息融合技术(Merge)以及基于Merge的Skip模式的帧间预测模式、自适应环路滤波等新技术[3], 这些技术的改进使得HEVC比H.264节省了50%左右的编码率[4]. 这些新的编码技术在提高编码效率的同时, 也增加了计算复杂度, 特别是编码器为获得最佳CU四叉树划分所采用的全深度搜索方法需要大量的计算时间, 这极大地提高了HEVC编码器的复杂度.
目前已经有一些研究学者针对CU四叉树划分计算复杂度高的问题提出众多优化算法来降低计算复杂度. 文献[5]提出了自适应 CU 深度遍历的算法, 利用空域相关性来预测当前编码块的深度值, 而大部分的编码块还是要遍历3个CU以上的深度, 所以该方法节省的时间相当有限. 文献[6]通过比较时空相邻 CU 的深度, 来判断是否可以跳过当前深度 CU 的预测编码. 文献[7]采用时域空域相结合的预测方式, 通过相邻编码块深度值加权方式来预测当前编码块的深度值. 虽然这种方法在很大程度上减少了遍历范围, 但没有考虑到不同视频序列之间的差异性. 文献[8]根据空域相关性自适应地决定当前 CU 深度的最大值和最小值. 显然, 这种仅根据空域的相关性的方法降低的复杂度是有限的, 且其预测深度值的准确度也不高. 文献[9–11]通过提前终止四叉树划分的遍历对CU结构进行快速决策, 依据当前待编码CU的率失真代价(RDcost)与阈值Thre间的大小, 判断是否要进行下一步的递归划分, 但当图像细节较多时提高的效率不高. 文献[12]在帧内预测前利用相邻已编码CU的深度对当前CU的深度进行预判断; 在帧内预测时利用当前CU的率失真代价与预先定义的阈值进行对比判断, 跳过一些不合适所属区域内容的编码单元尺寸类型的编码过程. 文献[13]提出一种基于时空相关性的编码单元深度决策算法. 融合关联帧编码单元的深度信息及当前帧相邻编码单元的深度信息, 从而预测当前编码单元的深度范围.
针对以上问题, 本文综合考虑了编码效率和时间损耗, 通过优化CU四叉树结构划分的遍历过程, 提出了一种CU结构快速划分算法. 通过考虑时空域的相关性和二分法的高效性对编码单元深度决策算进行改进法, 使得优化后的结果在基本不改变图像的质量与输出码率的情况下, 提高了编码时间.
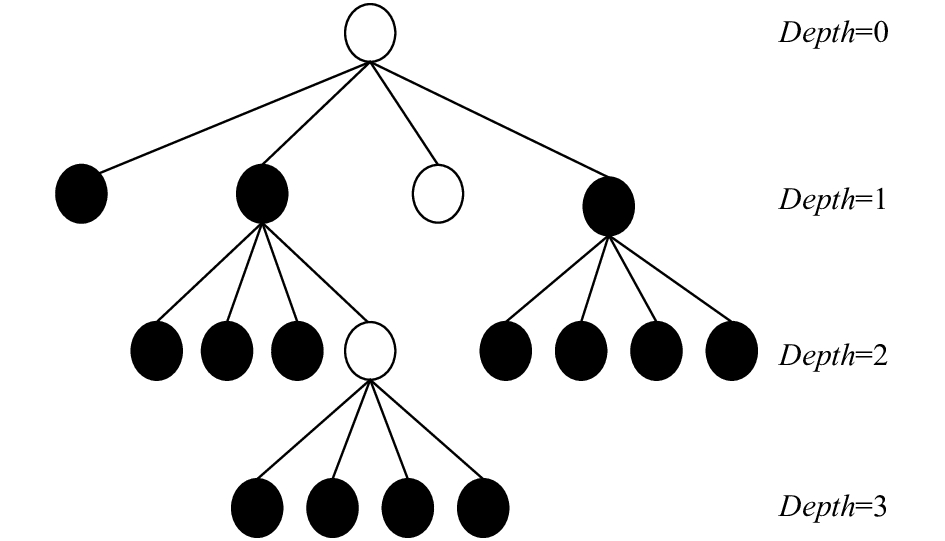
1 HEVC的CU深度决策为了灵活有效的表示视频编码内容, HEVC为图像的划分定义了一套全新的分割模式, 包括编码单元(Coding Unit, CU)、预测单元 (Prediction Unit, PU)和变换单元(Transform Unit, TU)3个概念描述整个编码过程.其中CU类似于 H.264 中的宏块或子宏块, 每个CU均为2N×2N的像素块, 是HEVC编码的基本单元, 目前可变范围为64×64至8×8. 图像首先以最大编码单元(LCU, 如64×64块)为单位进行编码, 在LCU内部按照四叉树结构进行子块划分, 直至成为最小编码单元(SCU, 如8×8块)为止, 对应的分割深度分别为 0、1、2 和 3, 如图1所示. 在HEVC 的编码过程中, 通过比较四叉树结构(图2)中本层CU 与下层 4个子CU的RDcost大小来决定 CU 是否需要划分, 进而决定 LCU 的最终划分方式, 如图2所示每一个CTU的四叉树递归划分过程如下.
步骤1. 首先进行CU的划分过程. 对于每个64×64深度Depth=0的最大编码单元LCU进行预测编码, 同时, 该CU还要进行各种PU预测和相应的模式选择, 最终根据公式(1)得到率失真代价.
| $RD{cos} t = SSE + \lambda \times bits\;\;\;\;$ | (1) |
其中, SSE表示使用预测模式计算的残差平方和, λ表示拉格朗日系数;bits表示使用当前预测模式下进行编码的码率.
步骤2. 将64×64的编码单元划分为4个32×32的子CU, 每个子CU的尺寸大小是32×32, 深度Depth=1. 同理对每个子单元进行预测编码, 并计算各自的率失真代价值. 如此递归的划分下去, 直至划分到最小的编码单元8×8, 深度Depth=3时便不再划分.
|
图 1 四叉树结构 |
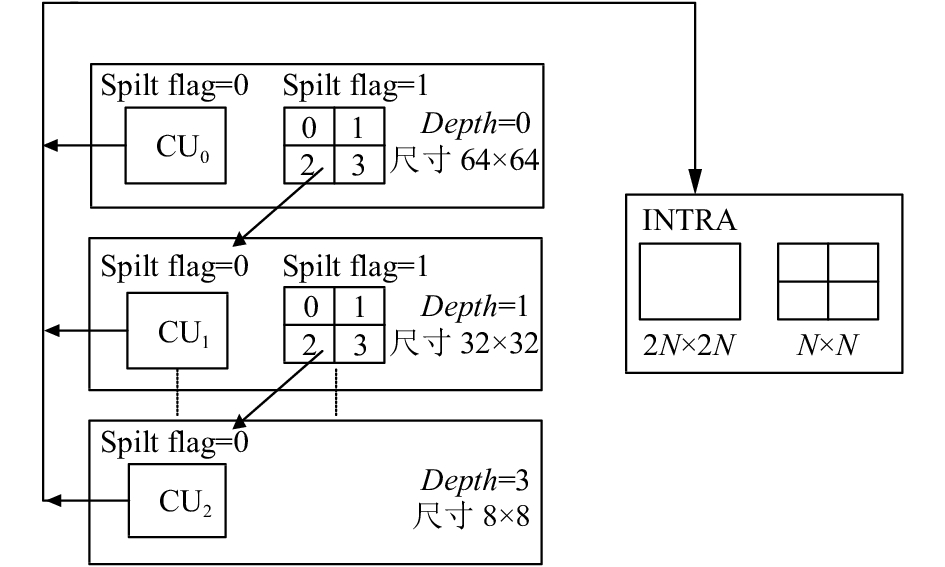
步骤3. 从Depth为0的CU开始进行CU深度划分过程, 如果4个32×32大小的子CU的率失真代价之和大于于其对应的64×64大小的CU的率失真代价, 则选择64×64的CU; 否则, 选择32×32的CU. 如此递归下去, 直到选到Depth为0的CU. 至此, 当前LCU的深度决策过程完成.
|
图 2 CU的深度分割示意图 |
为了能够获取最佳的块划分方式, HEVC编码器使用全深度搜索方法. 在确定一个LCU的最终深度算法中, 需要对CU深度进行0~3次的全遍历,总共需要进行1+4+4×4+4×4×4=85次CU尺寸选择的率失真代价计算, 而每个CU还要进行各种PU预测和模式选择的率失真代价计算. 这使得编码器的复杂度过高, 无法满足编码器的实时应用, 因此降低编码器的复杂度, 提高编码速度具有非常重要的应用价值.
2 算法介绍 2.1 帧间时空域的相关性由于在视频序列是由连续的图像序列帧构成, 则相邻帧之间具有很强的关联性, 即空间相关性的存在. 由于存在空间相关性, 因此HEVC编码帧与编码帧之间CU的分割方式也存在极强的关联性. 为了分析时空相邻CU划分深度的相关性, 首先通过5类官方的测试序列ClassA~E进行编码测试, 测试详情如表1所示. 时空相邻CU划分深度的相关统计结果如表2所示[14].
| 表 1 通用测试序列的详细情况 |
通过表2的数据分析可知, 当前CU的最优化分深度与前一帧相同位置的CU之间有较强的相关性, 因此可以利用前一帧相同位置的CU的划分深度对当前LCU的最优四叉树结构进行预测.
| 表 2 时空相邻CU的相关性(单位: %) |
2.2 二分深度划分决策算法
在HEVC视频编码标准中, 当视频图像比较平坦, 内容变化缓慢时, 针对它的编码单元大多选择了大尺寸类型; 当视频图像比较复杂, 细节比较丰富时, 针对它的编码单元大多选择了小尺寸类型; 使用HEVC测试模型HM15.0下对5类官方的测试序列ClassA~E进行编码测试, 通过统计分析出不同量化参数QP下编码单元CU的分布情况, 见表3.
| 表 3 不同QP下编码单元CU的分布(单位: %) |
从表3可以看出, 在测试序列中最小划分深度CU结构(64×64)仅仅占10%左右. 而在HM15.0中从划分深度最小的CU结构开始遍历, 那么大部分CU需要花费大量的时间效率进行层层遍历, 计算复杂度高. 因此通过对CU四叉树结构的遍历过程进行优化, 提出了一种二分深度划分决策算法, 从二分深度Depth=2(即CU的大小为16×16)开始遍历, 并在每一步遍历之前, 判断是否提前终止遍历.
2.3 二分深度划分算法整体算法描述如下:
1) 利用前一帧相同位置的CU的划分深度对当前LCU的最优四叉树结构进行预测.
2) 首先将二分深度CU(即CU的大小为16×16, Depth=2)的最佳预测模式作为最优RDcost模式, 以二分划分深度的CU作为最小CU结构.
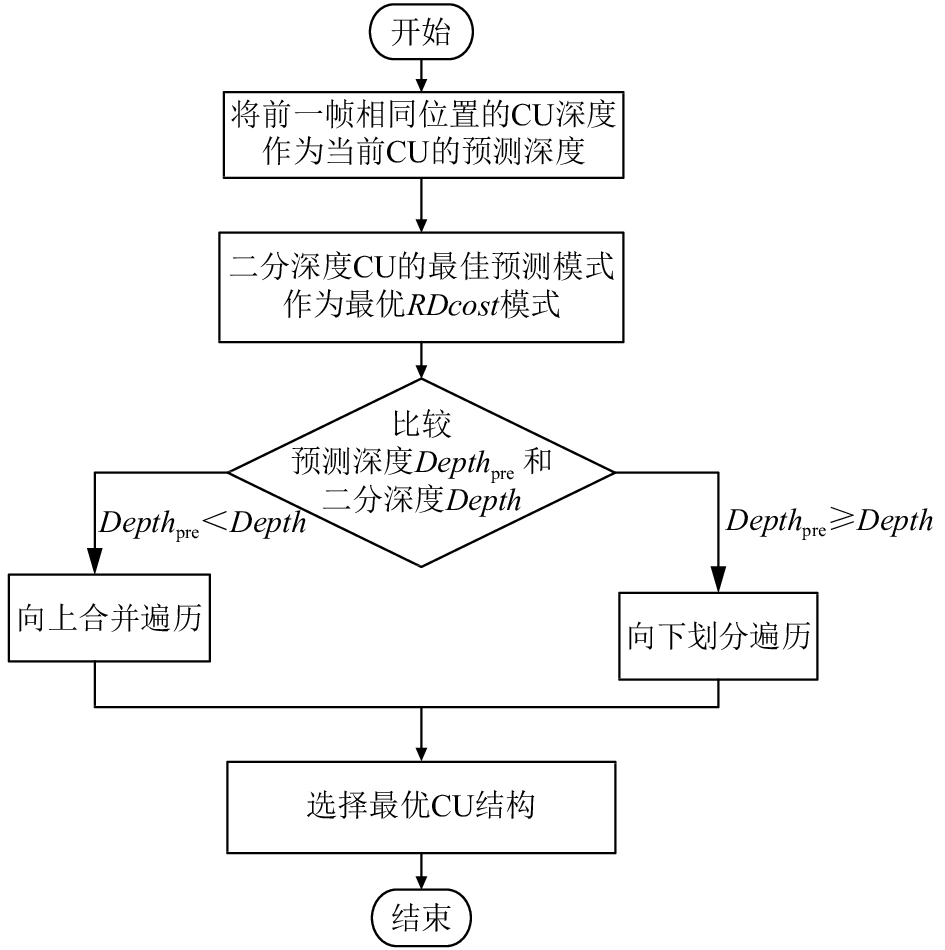
3) 将预测深度Depthpre和二分深度Depth进行比较(流程如图3所示). 若预测深度Depthpre ≥二分深度Depth, 则进行向下划分遍历, 跳转到4); 反之, 则进行向上合并遍历, 跳转到5).
|
图 3 二分深度划分算法流程 |
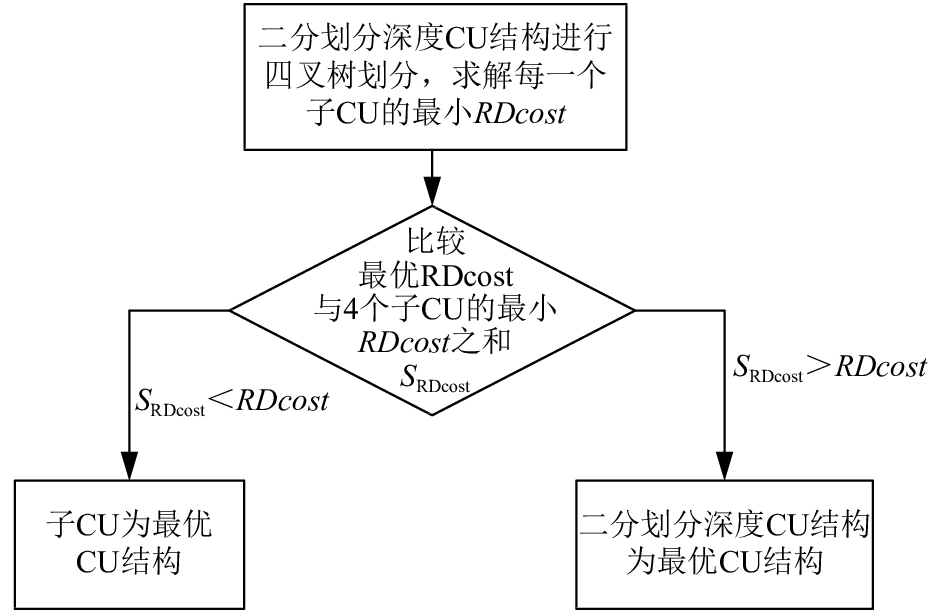
4) 若预测深度Depthpre >=二分深度 Depth, 则进行向下划分遍历(流程如图4所示). 首先以二分深度CU的最佳预测模式作为最优RDcost模式, 再对二分深度CU结构进行四叉树划分, 求解每一个子CU的最优RDcost, 并将最优RDcost与4个子CU的最小RDcost之和SRDcost进行比较: 若SRDcost较小, 则以4个子CU的最小RDcost之和作为最优RDcost, 以4个子CU作为最小CU结构; 若最优RDcost较小, 则停止当前CU子块的划分, 以当前CU作为当前CU子块的最优结构.
|
图 4 向下划分遍历算法流程 |
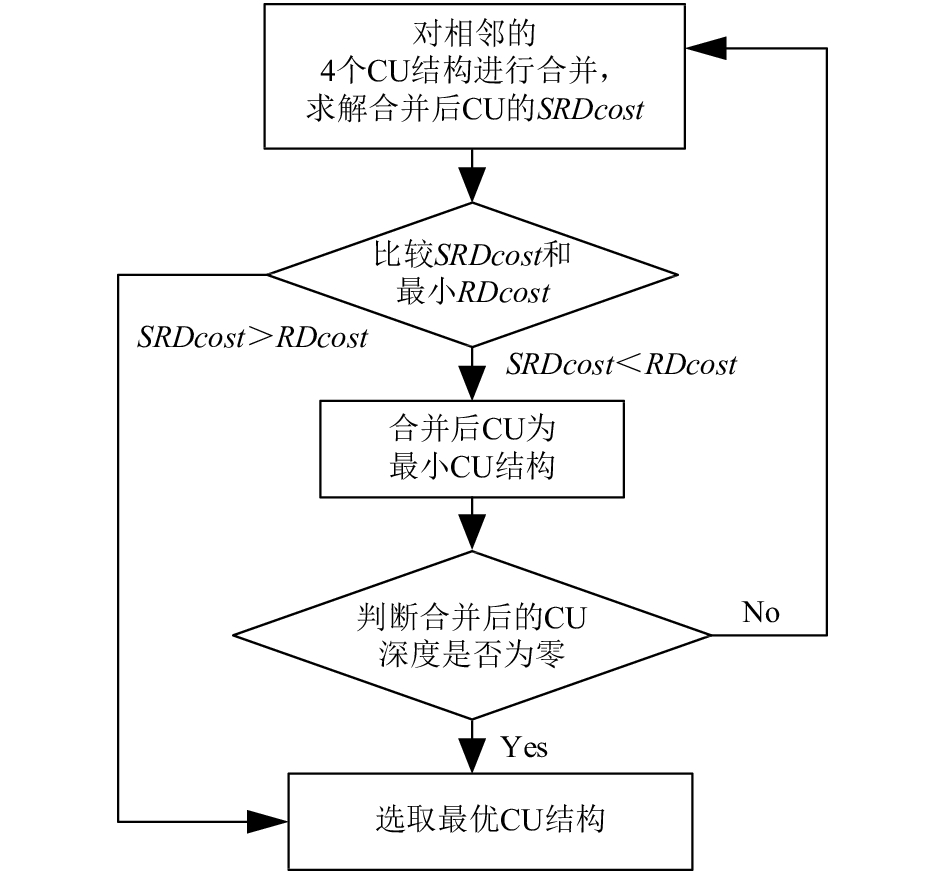
5)若预测深度Depthpre <二分深度 Depth, 则进行向上合并遍历(流程如图5所示). 对4个CU结构进行合并, 求解合并后CU的SRDcost, 并将其与最优RDcost进行比较: 若合并后CU的SRDcost较小, 则以合并后CU为最小CU结构, 并继续对周围相邻的4个CU进行合并; 若最优RDcost较小, 则停止当前CU子块的划分, 以当前CU作为最优结构.
|
图 5 向上合并遍历算法流程 |
3 实验结果与分析
为了验证本文所提出算法的效率, 以HEVC的软件测试模型HM15.0为参照进行实验. 实验平台为Inter(R)酷睿双核CPU, 主频2.60 GHz, 内存4.00 GB, 操作系统Windows7. 在此实验平台上采用11个通用序列分别进行验证, 测试QP(量化参数)为: 22, 27, 32, 37和42, 每个序列各测试100帧. 本文主要从所提出算法的编码效率以及付出的相应代价来考虑算法的性能.
通过比较编码效率的参数指标有峰值信噪比增量(ΔPSNR)、码率增量(ΔBitrate)和编码时间增量(ΔTime):
ΔPSNR是指本文所提快速算法与HM15.0算法的视频峰值信噪比之差, 即:
| $\begin{split}\Delta PS\!NR \!\!= &\displaystyle\frac{1}{5}\!\!\sum\limits_{i = 1}^5 {(PS\!N{R_{\rm {proposed}}}(QP) \!-\! PS\!N{R_{\rm {HM}}}(QP))} \\& \times 100\%\end{split}$ | (2) |
ΔBitrate是指本文所提快速算法视频的平均码率与HM15.0算法视频的平均码率之差, 即:
| $\begin{array}{l}\Delta Bitrate =\\\displaystyle\frac{1}{5}\sum\limits_{i = 1}^5 {\frac{{\left( {Bitrat{e_{\rm {proposed}}}\left( {Q{P_{{i}}}} \right) - Bitrat{e_{\rm {HM15.0}}}\left( {QP} \right)} \right)}}{{Bitrat{e_{\rm {proposed}}}\left( {Q{P_{{i}}}} \right)}}} \times100\%\end{array}$ | (3) |
ΔTime是指本文所提快速算法视频的平均编码时间与HM15.0算法视频的平均编码时间之差, 即:
| $\begin{array}{l}\Delta Time =\\\displaystyle\frac{1}{5}\sum\limits_{i = 1}^5 {\frac{{\left( {Tim{e_{\rm {proposed}}}\left( {Q{P_{{i}}}} \right) - Tim{e_{\rm {HM15.0}}}\left( {Q{P_{{i}}}} \right)} \right)}}{{Tim{e_{\rm {proposed}}}\left( {Q{P_{{i}}}} \right)}}} \times 100\%\end{array}$ | (4) |
从表4可以看出, 本文所提出的快速算法与HM15.0相比, 编码时间平均缩短了55.4%, 而编码码率平均仅增加了0.56%, 视频峰值信噪比仅降低了0.019%, 主观图像质量基本没有变化. 由此可见, HEVC编码CU快速划分算法在保证视频质量的前提下, 缩短了编码时间, 提高了编码效率.
| 表 4 编码性能的对比 |
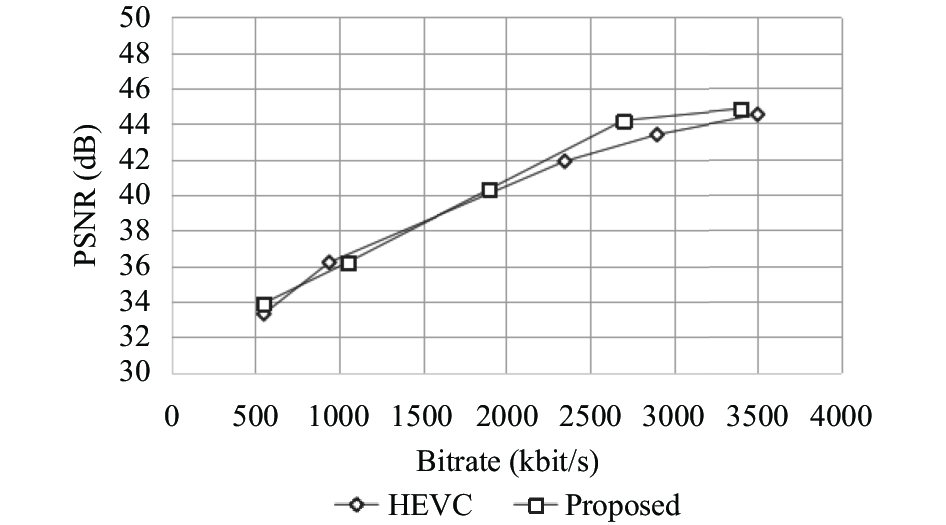
图6显示了本文提出的快速算法与HM15.0编码算的性能对比情况. 文中算法与HM15.0的率失真代价(RD)曲线基本重合, 表明本文算法与HM15.0的编码性能相比没有明显差异, 由此证明本文所提算法的有效性.
表5是本文快速算法以其他几种典型算法的编码性能对比. 根据表5 的对比, 不论是编码质量、码率, 还是编码时间, 本文提出的CU快速划分算法性能要比其他2种更优, 这得益于本文提出的二分深度划分技术, 降低了当前CU划分的时间消耗.
|
图 6 RaceHorse的率失真代价(RD)曲线图 |
| 表 5 本文快速算法与各典型算法的性能比较 |
4 结论
为降低算法遍历 HEVC编码单元CU结构的计算复杂度, 本文提出一种改进的HEVC编码单元CU快速划分算法. 本文算法首先预测当前CU的最优深度, 再通过二分深度划分算法进行深度遍历, 选出最优深度. 实验结果表明, 与HM15.0相比, 在编码质量几乎没有变化的情况下, 编码时间减少55.4%,能有效降低HEVC的编码复杂性.
| [1] |
Shen LQ, Zhang ZY, An P. Fast CU size decision and mode decision algorithm for HEVC intra coding. IEEE Transactions on Consumer Electronics, 2013, 59(1): 207-213. DOI:10.1109/TCE.2013.6490261 |
| [2] |
Sullivan GJ, Ohm JR, Han WJ, et al. Overview of the High Efficiency Video Coding (HEVC) standard. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12): 1649-1668. DOI:10.1109/TCSVT.2012.2221191 |
| [3] |
朱秀昌, 李欣, 陈杰. 新一代视频编码标准——HEVC. 南京邮电大学学报(自然科学版), 2013, 33(3): 1-11. |
| [4] |
黄胜, 付雄, 郝言明, 等. 一种HEVC帧内快速编码算法. 光电子·激光, 2017, 28(3): 296-303. |
| [5] |
Li X, An JC, Guo X, et al. Adaptive CU depth range. Proceedings of the 5th JCT-VC Meeting. Geneva, Switzerland. 2011.
|
| [6] |
李维, 张和仙, 杨付正. 高效率视频编码快速模式判决算法. 西安交通大学学报, 2013, 47(8): 104-109. DOI:10.7652/xjtuxb201308018 |
| [7] |
Cao XR, Lai CC, Wang YF, et al. Short distance intra coding scheme for HEVC. Proceedings of 2012 Picture Coding Symposium. Krakow, Poland. 2012. 501–504.
|
| [8] |
Mu FS, Song L, Yang XK, et al. Fast coding unit depth decision for HEVC. Proceedings of 2014 IEEE International Conference on Multimedia and Expo Workshops (ICMEW). Chengdu, China. 2014. 1–6.
|
| [9] |
Kim J, Choe Y, Kim YG. Fast coding unit size decision algorithm for intra coding in HEVC. Proceedings of 2013 IEEE International Conference on Consumer Electronics (ICCE). Las Vegas, NV, USA. 2013. 637–638.
|
| [10] |
齐美彬, 陈秀丽, 杨艳芳, 等. 高效率视频编码帧内预测编码单元划分快速算法. 电子与信息学报, 2014, 36(7): 1699-1705. |
| [11] |
白彩霞, 袁春. HEVC子划分快速决策算法. 第八届和谐人机环境联合学术会议. 广州, 中国. 2012. 23–28.
|
| [12] |
姚晓敏, 王万良, 岑跃峰, 等. 一种面向HEVC的编码单元深度决策算法. 计算机工程, 2015, 41(1): 240-244. |
| [13] |
蒋刚毅, 杨小祥, 彭宗举, 等. 高效视频编码的快速编码单元深度遍历选择和早期编码单元裁剪. 光学精密工程, 2014, 22(5): 1322-1330. |
| [14] |
李强, 覃杨微. 一种基于空时域相关性的HEVC帧间预测模式快速决策算法. 重庆邮电大学学报(自然科学版), 2016, 28(1): 9-16. DOI:10.3979/j.issn.1673-825X.2016.01.002 |
 2018, Vol. 27
2018, Vol. 27



