随着计算机技术和网络技术的发展, 信息安全的问题日益凸显[1]. 数字图像具有数据量大、空间有序、相关性强、冗余度高的特点[2], 使用传统的算法(DES、AES)时加密效率比较低. 混沌系统具有一些良好的特性, 使得其在图像加密领域越来越受欢迎. 当今有很多基于混沌系统的图像加密算法被提出.
Xu等人[3]提出一种对图像分块置乱以及对像素点动态索引进行扩散的图像加密算法; Norouzi等人[4]提出一种对行列分块置乱以及对位平面进行扩散的图像加密算法; Wang等人[5]根据混沌序列和万有引力定律提出了一种图像加密算法; Xu等人[6]根据混沌系统对经过位平面分解后的明文图像进行置乱与扩散. 这几种加密算法总体来说加密效果都不错, 但是混沌序列都与明文图像无关, 因此不能很好的抵抗选择明文攻击. 林等人[7]提出了一种基于位平面自适用参数的图像加密算法, 该算法产生混沌序列时引入了明文图像, 可以在一定程度上抵御选择明文攻击, 但是该算法只是简单的把图像灰度值的总和引入到混沌系统的初始值中, 算法的安全性还可以提高. 本文结合当今一些算法存在的安全性问题, 根据混沌系统、格雷码和SHA-384提出了一种基于置乱-扩散模式的图像加密算法. 实验结果表明, 该算法具有较好安全性.
2 算法基础 2.1本文中使用了
| $\left\{ \begin{gathered} {g_i} = {a_i}{\rm{ }},\;{\rm {if}}\;{\rm{ }}i > k - p - 2 \hfill \\ {g_i} = od (({a_i} + {a_{i + p + 1}}),n), \;{\rm{ if}}\;{\rm{ }}0 \leqslant i \leqslant k - p - 2 \hfill \\ \end{gathered} \right.$ | (1) |
上式中
在下文中, 规定
Lorenz系统的表达式如(2)所示.
| $\left\{ \begin{gathered} \dot x = a(y - x) \hfill \\ \dot y = cx - y - xz \hfill \\ \dot z = xy - bz \hfill \\ \end{gathered} \right.$ | (2) |
其中
在本文的加密算法中, 通过明文灰度值和SHA-384产生了一个384位的密钥. 把这384位的密钥按每8位为一个整数(
混沌系统的初始值计算如下:
| ${x_0} = {x_0}^\prime + od \left(\frac{{({k_1} \oplus ... \oplus {k_8}) + \displaystyle\sum\limits_{i = 1}^{48} {{k_i}} /48}}{{256}},1\right)$ | (3) |
| ${y_0} = {y_0}^\prime + od \left(\frac{{({k_9} \oplus ... \oplus {k_{16}}) + \displaystyle\sum\limits_{i = 1}^{48} {{k_i}} /48}}{{256}},1\right)$ | (4) |
| ${z_0} = {z_0}^\prime + \,od \,\left(\frac{{({k_{17}} \oplus \cdots \oplus {k_{24}}) + \displaystyle\sum\limits_{i = 1}^{48} {{k_i}} /48}}{{256}},1\right)$ | (5) |
其中
扩散部分的初始值计算如下:
| ${u_0} = od \left(\frac{{({k_{25}} \oplus ... \oplus {k_{32}}) + \displaystyle\sum\limits_{i = 1}^{48} {{k_i}} /48}}{{256}},1\right)$ | (6) |
| ${v_0} = \,od \,\left(\frac{{({k_{33}} \oplus ... \oplus {k_{40}}) + \displaystyle\sum\limits_{i = 1}^{48} {{k_i}} /48}}{{256}},1\right)$ | (7) |
步骤1. 假设明文图像和置乱图像长度都是M×N, 把图像转换成一维的数组, 选取数组长度的基数为2, 会得到M×N=2k.
步骤2. 令
步骤3. 对于
步骤4. 在明文图像中找到第
步骤5. 令
步骤1. 根据公式(2)、公式(3)、公式(4)和公式(5)产生长度为M×N的混沌序列X, Y, Z. 将序列X, Y转换为和矩阵B一样大小的二维矩阵X', Y'.
步骤2. 对矩阵X'逐行进行排序, 进而会得到排序以后的位置矩阵IR, 然后用矩阵IR对图像B逐行进行行置乱, 最后得到行置乱图像B1.
步骤3. 对矩阵Y'逐列进行排序, 进而会得到相应的位置矩阵IC, 然后用矩阵IC对矩阵B1逐列进行列置乱, 最后得到列置乱矩阵G.
3.3 像素扩散步骤1. 根据公式(6)、公式(7)获得两个初始值u0和v0, 同时设置控制参数b和c.
步骤2. 令i=0.
步骤3. 用下面的公式得到2个8位的整数值di和ei.
| ${d_i} = floor\left( {L \times {u_i}} \right)$ | (8) |
| ${e_i} = floor\left( {L \times {v_i}} \right)$ | (9) |
其中,
步骤4. 通过公式(10)和公式(11), 更改像素的灰度值:
| $H\left( {2i + 1} \right) = \Phi \left( {2i + 1} \right) \oplus od \left( {\left( {{d_i} + H\left( {2i} \right)} \right),L} \right)$ | (10) |
| $H\left( {2i + 2} \right) = \Phi \left( {2i + 2} \right) \oplus od \left( {\left( {{e_i} + H\left( {2i + 1} \right)} \right),L} \right)$ | (11) |
其中,
| $H\left( 0 \right) = floor\left( {\left( {k _{41} + \cdots + k _{44} } \right)/4} \right)$ | (12) |
步骤5. 通过改进的Arnold变换计算下一次的
| $t = od \left( {H\left( {2i + 1} \right),3} \right) + 1$ | (13) |
| $\left( \begin{array}{l}{u_{i + 1}}\\{v_{i + 1}}\end{array} \right) = od \left( {{{\left( {\begin{array}{*{20}{c}}1&b\\c&{1 + bc}\end{array}} \right)}^t}\left( \begin{array}{l}{u_i}\\{v_i}\end{array} \right),1} \right)$ | (14) |
步骤6. 令i=i+1, 重复步骤3–步骤5, 直到所有的像素点的灰度值都完成更改.
步骤7. 对3.2.2节步骤1中产生的混沌序列Z作如下的处理, 得到反向扩散序列W(i):
| $W\left( i \right) = od \left( {\left( {floor\left( {Z\left( i \right) \times {{10}^{14}}} \right)} \right),L} \right)$ | (15) |
其中, 1≤i≤M×N.
步骤8. 通过下面的公式反向改变像素的灰度值:
| $C\left( i \right) = C\left( {i + 1} \right) \oplus od \left( {\left( {H\left( i \right) + W\left( i \right)} \right),L} \right)$ | (16) |
其中,
| $C\left( {M \times N + 1} \right) = floor\left( {\left( {k _{45} + \cdots + k _{48} } \right)/4} \right)$ | (17) |
图1是整个加密过程的结构图. 解密过程与加密过程类似, 对密文图像实行相反的操作, 就可以恢复出明文图像.
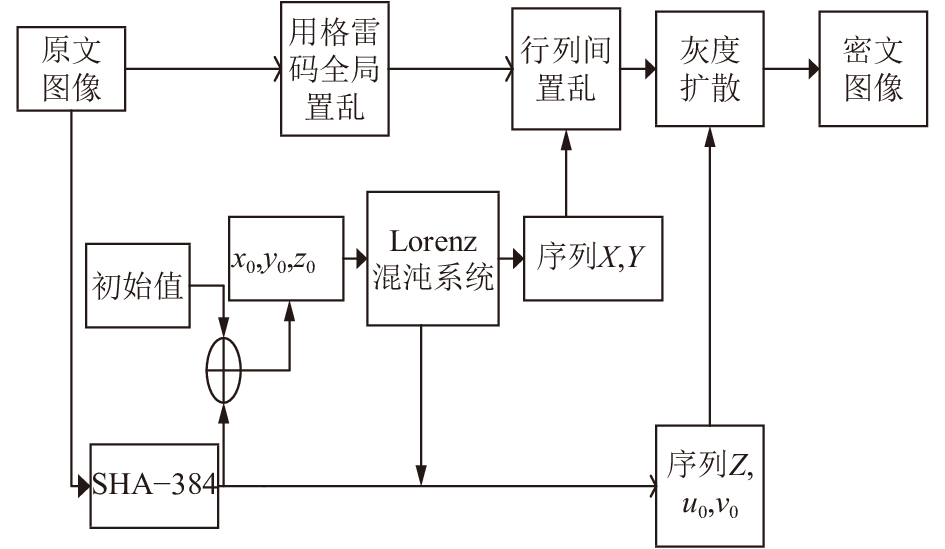
|
图 1 图像加密结构图 |
4 实验仿真与分析
在本文的仿真过程中, 选择了大小为256×256的Lena灰度图进行仿真. 在加密系统中设置参数

|
图 2 实验仿真图 |
4.1 图像直方图
图像的直方图可以用来表示图像中所有像素点灰度值的分布状况. 图3是明密文图像的直方图.
从图3(b)中可以看出密文图像的直方图分布的比较均匀, 说明该算法可以很好的掩盖明文图像的灰度统计特性.
4.2 相邻像素相关性相邻像素相关性表示的是图像中相邻像素间的相关水平. 如果相关性越低, 那么抵抗统计攻击的能力越强. 为了检验图像中两个相邻像素点之间的相关性, 分别在Lena明密文图像的水平、垂直以及对角线方向上随机抽取2000对相邻的像素点, 并计算相关系数, 结果如表1所示.

|
图 3 图像直方图分析 |
| 表 1 相邻像素相关系数及比较 |
表1中的数据, 数值越接近1表示相关性越高, 越接近0表示相关性越低. 通过比较, 本文的算法能有效的降低相邻像素点间的相关性.
4.3 密钥空间及敏感性一个好的加密算法应该是有一个足够大的密钥空间, 以抵抗穷举攻击. 本文的密钥主要由2部分构成: 给定的初始值
为了验证敏感性, 使初始值

|
图 4 密钥敏感性测试 |
4.4 差分攻击
图像加密中一般使用NPCR(像素变化率)、UACI(平均改变强度)来评价算法抗差分攻击的性能. 对于一幅256级的灰度图像, NPCR的值大于99.6094%, UACI的值大于33.4635%时算法才是安全的. 实验中随机选取了5个像素点, 其灰度值都改变1, 加密轮数为1轮, 计算相应的NPCR和UACI, 结果见表2, 均值见表3. 通过比较可以看出, 本文算法的NPCR和UCAI都能满足算法安全的要求, 从而可以较强的抵抗差分攻击.
| 表 2 不同位置的NPCR和UACI(单位: %) |
| 表 3 NPCR和UACI的均值及比较(单位: %) |
4.5 抗选择明文攻击分析
本文算法的中间密钥可以看作是矩阵IR和IC(置乱部分的中间密钥)、序列W(扩散部分的中间密钥), 而得到这3个中间密钥需要迭代混沌系统, 混沌系统的初始值与SHA-384和明文图像共同产生的散列值有关, 因此可以认为本文算法的中间密钥和原始图像有关. 选择不同的明文图像得出的中间密钥是不相同的, 因此以特定明文图像得出的中间密钥并不能破解其他的密文图像, 所以说本文算法可以较好的抵抗选择明文攻击.
4.6 剪切攻击在本文的算法中由于置乱过程的作用, 使得密文图像中被剪切掉的那部分相应的错误解密图像会均匀的分布在整个解密图像中, 因此密文图像即使受到剪切攻击后, 在解密图像中也可以看到明文图像的内容. 图5(a)为密文图像被剪切掉四分之一的面积, 图5(b)是相应的解密图像, 从图中可以看出, 即使密文图像有丢失, 解密图像中的内容大致也可以被识别, 因此可以认为本算法具有一定的抗剪切攻击的能力.
5 结论本文提出的图像加密算法有以下三个特点: 首先, 使用SHA-384和明文图像产生加密过程的密钥, 使混沌序列与明文图像有关, 能更好的抵抗选择明文攻击, 同时增大了密钥空间; 其次, 算法在置乱阶段使用了基于格雷码和混沌序列相结合的置乱方法, 可以更好的实现置乱效果; 最后, 算法中加入了正反向的扩散操作, 使得密文图像中的像素点与前后像素点有关, 能更好的掩盖图像的灰度统计特性. 实验结果表明, 本文的算法具有较好的安全性, 在图像传输领域有一定的潜在应用价值.

|
图 5 抗剪切测试 |
| [1] |
毛骁骁, 孙克辉, 刘文浩. 基于分数阶统一混沌系统的图像加密算法. 传感器与微系统, 2017, 36(6): 138-141. |
| [2] |
文昌辞, 王沁, 苗晓宁, 等. 数字图像加密综述. 计算机科学, 2012, 39(12): 6-9, 24. DOI:10.3969/j.issn.1002-137X.2012.12.002 |
| [3] |
Xu L, Gou X, Li Z, et al. A novel chaotic image encryption algorithm using block scrambling and dynamic index based diffusion. Optics and Lasers in Engineering, 2017(91): 41-52. DOI:10.1016/j.optlaseng.2016.10.012 |
| [4] |
Norouzi B, Seyedzadeh SM, Mirzakuchaki S, et al. A novel image encryption based on row-column, masking and main diffusion processes with hyper chaos. Multimedia Tools and Applications, 2015, 74(3): 781-811. DOI:10.1007/s11042-013-1699-y |
| [5] |
Wang XY, Wei N, Zhang DD. A novel image encryption algorithm based on chaotic system and improved gravity model. Optics Communications, 2015(338): 209-217. DOI:10.1016/j.optcom.2014.10.042 |
| [6] |
Xu L, Li Z, Li J, et al. A novel bit-level image encryption algorithm based on chaotic maps. Optics and Lasers in Engineering, 2016(78): 17-25. DOI:10.1016/j.optlaseng.2015.09.007 |
| [7] |
林振荣, 倪骍波, 谌志涛. 基于位平面的自适应参数图像加密算法. 计算机工程与设计, 2016, 37(3): 597-601, 642. |
| [8] |
Zhou YC, Panetta K, Agaian S, et al. (n, k, p)-Gray code for image systems. IEEE Transactions on Cybernetics, 2013, 43(2): 515-529. DOI:10.1109/TSMCB.2012.2210706 |
 2018, Vol. 27
2018, Vol. 27



