近年来, 在电力系统中, 电网移动互联建设快速发展, 随之而来的基于云平台和移动公共服务的全过程配网作业管控系统应运而生. 配网作业管控系统可实现对现场作业的管理和实时监控. 作为配网作业智能管控系统的关键节点——智能终端, 在整个系统中起着重要作用. 智能终端的定位及移动轨迹是实现现场作业的管理和实时监控的必备功能.

现有的电力作业智能终端采用GPS进行定位, 此类方法主要通过由己知的卫星坐标及到达移动终端的时间、角度测量值来计算所在位置. 在移动环境下, 无线电波易受信号干扰, 受建筑物、树木遮挡等因素影响, 存在散射或反射影响, 使电波传播发生了很大延迟, 从而使发送端与接收端之间的距离或相应的距离差无法较为准确的测量^[1], 并且测得的定位位置和轨迹记录存在漂移现象. 在没有GPS信号或者GPS卫星数量不足的情况下, GPS难以实现有效定位^[2], 导致在监控中心出现智能终端移动轨迹紊乱, 甚至智能终端消失的情况也时有发生, 严重影响了系统可靠性和使用效果.

为解决上述问题, 不同的技术方法也随即涌现, 常用的方法有加权平均^[3]、卡尔曼滤波^[4,5]、自适应滤波^[6]、信息融合方法^[7–14]等. 加权平均是比较简单粗略的方法, 在长时间干扰或者无信号时, 误差依然严重. 卡尔曼滤波在大多条件下具备较好的滤波效果, 能有效剔除异常数据, 但在GPS智能终端大范围机动或信号被干扰时, 会带来较大误差. Saga-Husa自适应滤波算法状态变量的维数较高, 并且要计算系统噪声统计特性, 计算量大, 实时性、收敛性和稳定性难以保证, 不适用于对动态目标的定位^[6]. 强跟踪kalman自适应滤波算法滤波收敛性有所增强, 但破坏了滤波器的最优条件, 易导致滤波结果的波动, 影响滤波精度^[6]. 近年来基于滤波方法的信息融合定位^[11–13]虽然能改善滤波效果, 提高预测精度, 但在GPS信号干扰严重或者无法接收到GPS信号的情况下仍然难以在本质上改善定位效果. 文献[7–10]提出了在GPS+PDR 组合的基础上, 用卡尔曼滤波对GPS 和PDR数据进行融合, 因采用的卡尔曼滤波所假定的信号噪声为高斯白噪声, 且没有对PDR的有效误差校正, 会产生滤波结果偏差和积累误差, 导致定位精度下降.

本文提出了AGPS、无线基站定位和行人航位推测相结合的基于粒子滤波的定位系统, 实现在GPS信号较弱或者无信号的条件下, 智能终端依然可完成高精度定位.

1 基于信息融合的定位算法原理

本文采用基于信息融合的定位方法, 即采用”AGPS+无线基站信号+行人航位推测+粒子滤波算法”实现融合定位, 其原理如图1所示, 其步骤如下:

步骤1. 智能终端的磁力计、陀螺仪完成角度测量、加速度传感器实现加速度测量, 通过两者测量的数据计算去除重力并以地面作为参考系的加速度值.

步骤2. 根据加速度检测值, 利用基于零速更新的步长检测算法(Zero Velocity Update, ZUPT)实现步长检测.

步骤3. 根据陀螺仪完成的角度测量及步骤2实现的步长检测, 实现行人航位(位置)推测.

步骤4. 根据信号强度——距离数学模型, 测量智能终端与基站间距离, 根据AGPS观测值并结合无线基站测算, 计算坐标位置.

步骤5. 针对步骤3、步骤4的测量结果进行信息融合, 利用粒子滤波算法预测智能终端当前位置, 并输出定位结果.

2 航位推测(PDR)定位算法 2.1 步长检测

假设智能终端内带的加速度传感器以自身坐标的加速度为 ${a_{tilted\_x}}$ , ${a_{tilted\_y}}$ , ${a_{tilted\_z}}$ , 以地面为坐标的去除重力后对应的加速度 $a$ 在三方向上的分量为 ${a_x}$ , ${a_y}$ , ${a_z}$ , 陀螺仪完成的角度测量对应的偏航角 $\varphi $ , 俯仰角 $\theta $ , 滚转角 $\gamma $ , 则:

$a = \left[ {\begin{array}{*{20}{c}} {{a_x}} \\ {{a_y}} \\ {{a_z}} \end{array}} \right] = {R_S}\left[ {\begin{array}{*{20}{c}} {{a_{tilted\_x}}} \\ {{a_{tilted\_y}}} \\ {{a_{tilted\_z}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{g_x}} \\ {{g_y}} \\ {{g_z}} \end{array}} \right]$

(1)

其中, ${R_S} = {R_{\rm{E}}}{R_{\rm{N}}}{R_{\rm{D}}}$ , E代表东, N代表北, D代表指向地, ${R_S}$ 表示为:

${R_S} = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \varphi }&{\cos \theta \sin \varphi }&{ - \sin \theta } \\ {\sin \gamma \sin \theta \cos \varphi - \cos \gamma \sin \varphi }&{\sin \gamma \sin \theta \sin \varphi + \cos \gamma \cos \varphi }&{\sin \gamma \cos \theta } \\ {\cos \gamma \sin \theta \cos \varphi + \sin \gamma \sin \varphi }&{\cos \gamma \sin \theta \sin \varphi - \sin \gamma \cos \varphi }&{\cos \gamma \cos \theta } \end{array}} \right]$

(2)

假设从加速度传感器读取加速度采样值的频率为 ${f_s}$ , 则对应的速度为:

${v_i} = {v_{i - 1}} + a/{f_s}$

(3)

只通过加速度对采样频率的除法运算得到的速度值, 会随着时间的积累产生漂移, 从而生产较大的误差, 因此采用零速更新的步长修正.

假设 ${\mu _k}$ 为在第 $k$ 个姿态附近的平均速度, 则:

${\mu _k} = \sum\limits_{j = {i_k} - w}^{{i_k} + w} {\frac{{{v_j}}}{{2w + 1}}} $

(4)

式中 ${i_k}$ 为第 $k$ 个姿态时的采样索引, $w$ 为平均窗口取值, 为一常数. 假设 ${m_k}$ 为在第 $k$ 个姿态内的总采样数, 则通过线性积分求得在连续的姿态间的速度为:

${\hat v_{_i}} = {v_i} - [{\mu _k}(i - {i_{k - 1}}) + {\mu _{k - 1}}({i_k} - i)]/{m_k}$

(5)

则在第 $k$ 个姿态/脚步的位置增量 $ \Delta {P_k} = (\Delta {P_{k{\rm{N}}}},\Delta {P_{k{\rm{E}}}},$ $\Delta {P_{k{\rm{D}}}})$ 可表示为:

$\Delta {P_k} = \sum\limits_{j = {i_{k - 1}}}^{{i_k}} {{{\hat v}_j}/{f_s}} $

(6)

在水平二维空间, 步长可表示为:

$S{L_{ZUP{T_k}}} = \sqrt {\Delta {P_{kN}}^2 + \Delta {P_{kE}}^2}$

(7)

2.2 行人航位推测

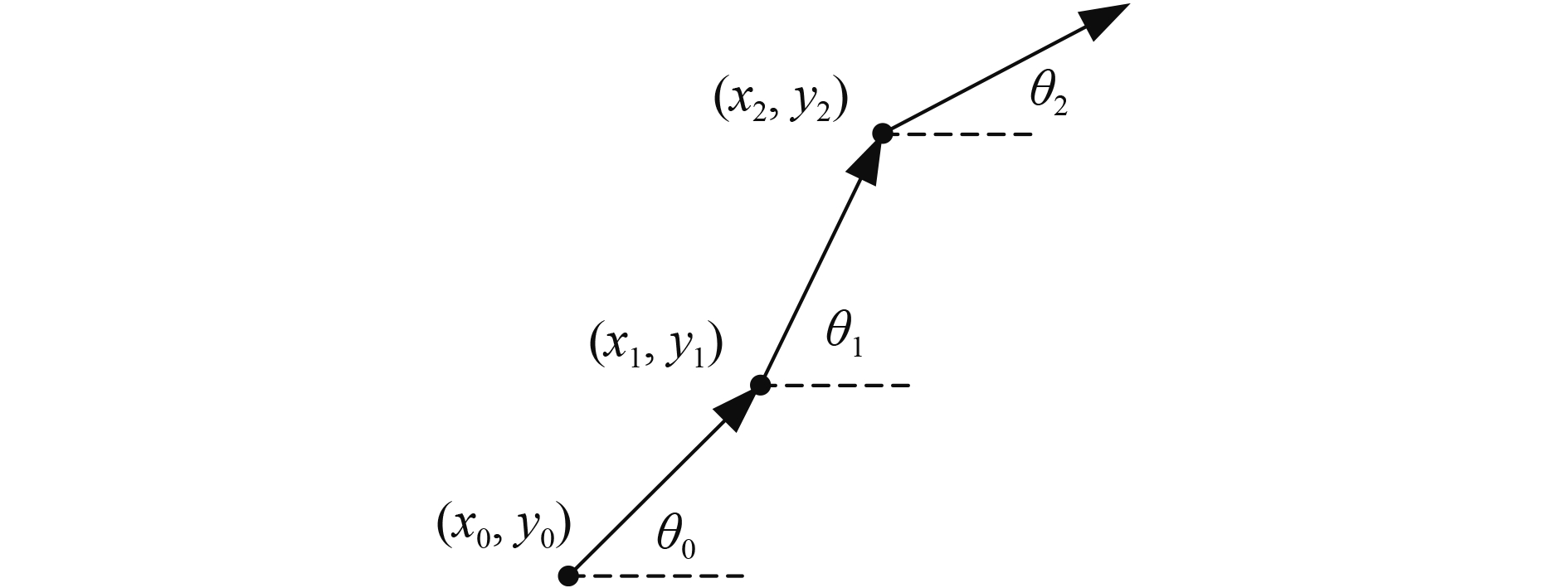
方向角和位移推测航迹原理如图2所示. 航向角 ${\theta _i}$ ( $i = 0,1,2, \cdots $ )为陀螺仪和磁力计组合测量得到的磁力线朝北方向和行走方向的夹角. 因此有:

$\begin{split}& {x_n} = {x_0} - \sum\limits_{i = 0}^{n - 1} {S{L_{ZUP{T_i}}}\sin {\theta _i}} \\& {y_n} = {y_0} - \sum\limits_{i = 0}^{n - 1} {S{L_{ZUP{T_i}}}\cos {\theta _i}} \end{split}$

(8)

3 AGPS/基站信号强度融合定位

基站无线信号强度R与通信距离d的关系可表示为:

$R = \alpha + 10\beta {\log _{10}}(\left| {d - {d_{AP}}} \right|) + noise$

(9)

式中, $\alpha $ 为离 ${d_{AP}}$ 1米处的信号强度, $\beta $ 为衰减系数, ${d_{AP}}$ 为基站节点所在位置, $d$ 为被测点所在位置, $noise$ 为高斯测量误差. ${d_{AP}}$ , $\alpha $ , $\beta $ 为已知量.

假设第 $k$ 个( $k = 1,2,3,4,\cdots $ )基站节点的位置 ${d_{AP}}$ 坐标为 $({x_{APk}},{y_{APk}})$ , 智能终端所在位置 $d$ 坐标为 $({x_d},{y_d},{z_d})$ , ${d_k}$ 为 $k$ 个节点到被测点的距离, 有:

${({x_{APk}} - {x_d})^2} + {({y_{APk}} - {y_d})^2} + {({z_{APk}} - {z_d})^2} = d_k^2$

(10)

针对基站信号, 若不考虑高度, 取 $k = 3$ , 则

$\left| {\begin{array}{*{20}{c}} {x{}_d} \\ {{y_d}} \end{array}} \right| = {A^{ - 1}}b = \left[ {\begin{aligned} {\frac{{{K_1}}}{K}({y_{AP2}} - {y_{AP3}}) + \frac{{{K_2}}}{K}({y_{AP3}} - {y_{AP1}})} \\ {\frac{{{K_1}}}{K}({x_{AP3}} - {x_{AP2}}) + \frac{{{K_2}}}{K}({x_{AP1}} - {x_{AP3}})} \end{aligned}} \right]$

(11)

其中,

$\begin{aligned}K = & 2({x_{AP1}} - {x_{AP3}})({y_{AP2}} - {y_{AP3}})\\& - 2({x_{AP2}} - {x_{AP3}})({y_{AP1}} - {y_{AP3}})\end{aligned}$

(12)

${K_1} = x_{_{AP1}}^2 - x_{_{AP3}}^2 + y_{_{AP1}}^2 - y_{_{AP3}}^2 + d_3^2 - d_1^2$

(13)

${K_2} = x_{_{AP2}}^2 - x_{_{AP3}}^2 + y_{_{AP2}}^2 - y_{_{AP3}}^2 + d_3^2 - d_2^2$

(14)

通过式(11)可求得被测点所在位置 $d$ 坐标为 $({x_d},{y_d})$ .

AGPS观测方程为:

${P_k} = \sqrt {{{\left( {X_k^{SV} - {x_d}} \right)}^2} + {{\left( {Y_k^{SV} - {y_d}} \right)}^2} + {{\left( {Z_k^{SV} - {z_d}} \right)}^2}} + b$

(15)

在恶劣条件下, AGPS定位系统和无线通信网络都无法独自有效定位时, 可融合GPS测得的伪距和无线通信网络中的终端测得位置实现定位的算法^[15]. 令 $\delta $ 为智能终端到初始观测值距离差, 即 $\delta = {\left[ {\Delta x,\Delta y,\Delta z} \right]^{\rm{T}}}$ , 则有:

$\delta = {\left( {{G^t}{Q^{ - 1}}G} \right)^{ - 1}}{G^{\rm{T}}}{Q^{ - 1}}h$

(16)

其中, $G$ 、 $Q$ 、 $h$ 由文献[15,16]给出, 根据式(16)可迭代得到终端的位置估计 $d$ 坐标, 算得的δ加上初始值即得下一迭代的初始值.

4 基于粒子滤波的定位预测

与卡尔曼滤波、扩展卡尔曼滤波相比, 粒子滤波用随机采样的粒子表达概率密度分布, 而不假设状态变量为高斯随机变量, 因此在处理非高斯问题、非线性上具有优势^[17]. 基于粒子滤波的位置预测如图3所示.

根据行人航位推测PDR的预测模型可由式(8)得:

${\hat X^{(j)}}[i] = {X^{(j)}}[i - 1] + \Delta X[i]$

(17)

式中, ${\hat X^{(j)}}(i)$ 表示当前的预测位置, ${X^{(j)}}[i - 1]$ 为上一次预测位置, $\Delta X[i] = S{L_{ZUP{T_i}}}\left[ {\begin{array}{*{20}{c}} {\sin {\theta _i}} \\ {\cos {\theta _i}} \end{array}} \right]$ .

无线测距预测模型似然函数:

$P(R[i]|\hat d[i]) = \prod\limits_{m = 1}^M {\frac{1}{{\sqrt {2\pi } \sigma }}} \left( { - \frac{{{{\left| {\Delta {R_m}[i]} \right|}^2}}}{{2{\sigma ^2}}}} \right)$

(18)

式中, $\sigma $ 为正态分布的方差, ${\hat d^{(j)}}[i]$ 为根据第3小节测算的位置, 可由式(9)得:

$\Delta {R_m}[i] = R[i] - (\alpha + 10\beta {\log _{10}}(\left| {d[i] - {d_{AP}}} \right|))$

(19)

式中, $R[i]$ 为读取的无线信号强度, $\alpha $ 、 $\beta $ 为经验值. 粒子权重为:

${w^{(j)}}[i] = {w^{(j)}}[i - 1]p(R[i]|\hat d[i]) \cdot {\gamma _n}$

(20)

${\gamma _n}$ 为对应WiFi、蓝牙信号的权值, 且 ${\gamma _1} + {\gamma _2} + $ $ \cdots +{\gamma _n} = 1$ .

估计状态的输出为:

$\hat X = \sum\limits_{j = 1}^N {{X^{(j)}}[i]} {\omega ^{(j)}}[i]$

(21)

5 实验结果与分析 5.1 基于零速更新(ZUPT)的步长检测算法

图4为系统读取加速度并对其积分后的速度曲线. 红色三角曲线、蓝色圆点曲线分别表示有ZUPT和没有ZUPT算法作用下的速度值比较, 由图可看出, 在没有ZUPT算法作用下的速度值会随着时间的增大, 误差明显增大, 而在有ZUPT算法作用下的速度值并无明显累计误差.

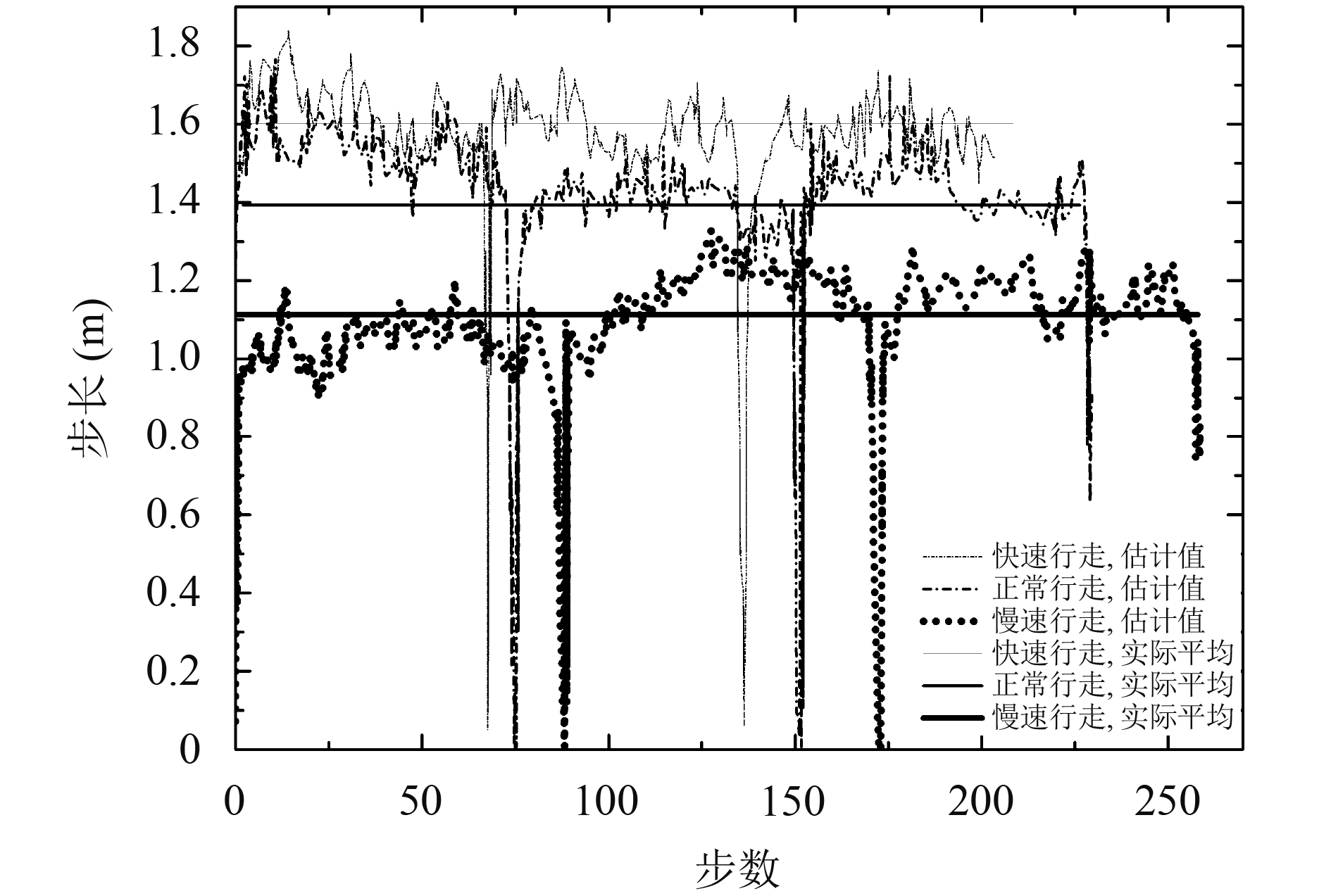
如图5所示为基于ZUPT的步长检测算法进行了实验测试. 在3种不同的步速情况下对步长进行了估计. 最粗的曲线表示慢速行走, 最细的曲线表示快速行走, 粗细中等的曲线表示正常行走, 实线表示实际的平均值, 虚线表示利用算法进行的估计. 从图中可以看出, 虚线所表示的检测估计基本上在实线所表示的实际平均值上下浮动.

表1为在行走100米的情况下, 3种步速的累积误差, 快速行走比慢走所测量的误差小, 正常行走的误差在两者之间.

5.2 不同定位预测算法比较

图6为不同定位方法的均方根误差(RMSE)比较, 步行距离为1000米, 步行速度有快、慢、正常, 实验在室外展开. “破折-点”线表示采用基于无线信号强度和行人航位推测的粒子滤波算法均方根误差, 细实线表示只采用行人航位推测的均方根误差, 粗实线表示只采用无线信号强度(AGPS+无线基站)实现定位的均方根误差. 从图中可知, 只采用无线信号强度(AGPS+无线基站)实现定位的均方根误差在较大的误差范围内波动, 只采用行人航位推测实现定位的均方根误差随着步行推进, 存在积累误差. 采用基于AGPS+无线基站和行人航位推测的粒子滤波算法实现的融合定位, 均方根误差随着粒子推进, 误差明显减小, 在行走状态下, 误差控制在0.8米以内.

为进一步验证在GPS信号较弱或者无GPS信号下的定位精度, 实验在室内(室内无GPS信号)特定设置的5×5米区域进行测试. 基于AGPS+无线基站和行人航位推测的粒子滤波算法实现的融合定位实测数据如图7所示. 带星曲线(红色)为实测数据, 圆点直线(黑色)为理论数据, 数据表明, 实测值基本在理论数据附近, 精度可控制在1米以内, 满足实际定位精度要求.

6 结束语

本文提出一种AGPS/无线基站网络、行人航位推测相结合的粒子滤波定位算法. 在单独采用AGPS或者基站定位方法时, 在没有足够观测量而无法精确定位时, 通过AGPS/无线基站网络、行人航位推测相结合的信息融合定位方法, 实现了电网作业智能终端的高精度定位. 实验表明, 在室外环境, 定位精度可控制在0.8米以内, 在室内精度可控制在1米以内.