列车停站方案是列车开行方案的基本内容, 停站方案的优化是保证列车开行方案合理化的必要环节. 优化列车停站方案可以方便游客出行, 节约游客出行时间, 满足旅客的多方面需要, 从而吸引节点客流, 提高铁路运输部门的运营收益, 降低营运成本^[1]. 为了能更好的为铁路运输组织提供辅助决策, 亟待解决列车停站方案优化问题.

停站方案模型的求解主要包括数学解析法和智能优化算法^[2]. 数学解析法虽然精确能保证解的质量, 但很难在有效时间内获得最优解, 且算法复杂度高. Wang等人^[3]将粒子群算法与模拟退火算法结合, 利用模拟退火算法的局部搜索能力提高了粒子群算法的搜索效率. 陈世明等人^[4]将捕食策略引入到粒子群算法中, 并提出一种自适应速度限制方式, 使得算法在大范围搜索时更易跳出局部最小解. 严艺等人^[5]对基本的遗传算法进行FPDC法和MOGA法相结合实现算法的改进, 并用来求解列车开行方案多目标规划模型.

近年来, 粒子群算法(PSO)凭借其易实现, 算法效率高等特点获得了广泛的应用. Liu^[6]提出了动态算法权重及异步调整学习因子的方法来优化分数阶控制器参数, 得到了较好的优化参数. Ali等人^[7]针对大规模优化问题, 提出一种基于三种机制的混合粒子优化与遗传算法, 该算法将粒子群算法用于平衡探测和开发阶段. Lin等人^[8]通过混合遗传粒子群算法来设计多域二进制过滤器, 该算法包括自适应参数, 重组, 变异操作. Wu等人^[9]在面向服务的制造业多任务调度问题中, 提出了一种混合离散粒子群优化遗传算法, 算法采用整数编码来建立粒子位置矩阵和服务位置方案的关联, 根据自我认识能力, 社会认识能力及以前的速度和位置来更新位置, 同时引入遗传算法的交叉和变异操作来适应离散空间, 实验证明所提算法的有效性. 粒子群算法通过保存个体最优和集体最优来完成极值寻优, 算法复杂度低且收敛速度较快, 但是随着迭代次数的增多, 存在粒子相似度高、易陷入收敛于局部最优等问题^[10]. 量子遗传算法利用量子比特的概率幅进行染色体编码, 并引入量子门机制对染色体进行更新^[11], 通过量子选择、交叉、变异等算子来改变种群的染色体信息, 但是量子遗传算法在解决复杂优化问题时会存在全局搜索能力极强而局部搜索能力较差和早熟收敛等缺点.

针对以上这些问题, 本文将粒子群算法与量子遗传算法相结合, 提出了一种改进的多目标混合粒子群算法(QGA_PSO). 算法在粒子群算法的基础上, 引入量子遗传算法的量子比特编码、量子旋转门及量子交叉和变异. 在利用旋转门更新粒子时, 直接将速度更新公式应用于角度更新, 而不是将速度更新公式作为角度的增量表达式, 加快了收敛速度. 另外, 该算法还加入了遗传算法的交叉和变异算子, 丰富了粒子的多样性, 使粒子跳出局部最优解. 最后通过一个实例证明了该方法的有效性, 期望能为该城际铁路列车停站方案的制定和优化提供有效的科学依据.

1 高速铁路列车停站方案模型

假设高速铁路旅客运输网络 $N = (S,T)$ . 其中 $S = \left\{ {{s_i}|i = 1,2, \cdots ,N} \right\}$ 为列车途经车站的集合, i代表车站在铁路线上的空间顺序, $T = \left\{ {{t_k}|k = 1,2, \cdots ,K} \right\}$ 为列车的集合.

${X_{ki}} = \left\{ {{x_{ki}}|k = 1,2, \cdots ,K;i = 1,2, \cdots ,N;{x_{ki}} = 0\;{\rm{or}}\;1} \right\}$

式(1)表示列车t_k在车站s_i是否停站, 0表示不停, 1表示停.

现假设有起讫点相同, 流量大小已知的客流, 在输送完所有客流的条件下, 为使旅客旅行时间最小同时区段可达性最大, 减少铁路运输企业的费用, 建立了如下所示的列车停站方案多目标多约束模型:

目标函数1. 旅客旅行时间最少

$\min \;{Z_1} = \sum\limits_t {\sum\limits_i {\sum\limits_j {\left\{ {{q_{t,i,j}}\sum\limits_{i < h < j,i \in {S_t},j \in {S_t}} {\left[ {{x_{t,h}}{w_h}} \right]} } \right\}} } } $

(1)

其中, ${q_{t,i,j}}$ 表示列车t从i站到j站的在途旅客量, w_h表示列车在h站的停车耗费时间, ${x_{t,h}}$ 表示列车t在h站停站与否. 一般情况下, 列车等级相同, 停站次数也相同, 旅行时间相差较小, 因此可以用旅客乘车区间的停站等待时间来代替实际旅行所花费的时间. 即把各个乘车区间在途旅客等待时间最小作为模型的优化目标.

目标函数2. 区段可达性最大化

$\max \;{Z_2} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{n - 1} {\sum\limits_{k = j + 1}^n {{\alpha _j}{\alpha _k}{x_{ij}}{x_{ik}}} } } $

(2)

α_j表示车站S_j的等级系数, 指标越大, 表示该车站等级越高. 区段可达性使得该区间所开行的列车在车站等级系数越大的车站停站次数越多.

列车能力约束:

${c_t} \ge \mathop {\max }\limits_{1 \le m \le n - 1} \left\{ {\sum\limits_i {\sum\limits_j {{q_{t,i,j}}{\xi _{i,j,m}}} } } \right\}$

(3)

${\xi _{i,j,m}}$ 表示第m个区间是否在i站与j站之间, 是为1, 不是为0. c_t表示列车定员. 确保列车各个区间的客流量都不超过列车定员.

客流量约束:

${q_{i,j}} \ge \sum\limits_t {{q_{t,i,j}}} $

(4)

$\min \left( {{{\rm{x}}_{t,i}},{x_{t,j}}} \right){q_{i,j}} \ge {q_{t,i,j}} \ge 0$

(5)

客流量约束, 将OD客流加载到列车上, 满足OD的最大服务频率.

停站总次数约束:

${h_{\min }}({\rm{j}}) \le \sum\limits_{i = 1}^m {{x_{ij}} \le {h_{\max }}(j)} \;,j = 1,2, \cdots ,N$

(6)

式(6)为列车途经各车站的停站总次数约束, 由于列车的停站方式对车站的通行能力有很大影响, 而停站次数也会影响列车的旅行速度. 因此可以根据客流量计算各车站的停站次数上下限值.

2 混合粒子群算法优化 2.1 粒子群算法原理^[12]

粒子群算法通过模仿自然界动物的行为来寻找最优解. 在粒子群算法中, 每个优化问题的解都是搜索空间中的一只鸟, 我们称之为“粒子”. 粒子群算法初始化为一群随机粒子(随机解). 然后通过迭代找到最优解. 在每一次迭代中, 通过计算更新粒子速度和位置信息, 更新个体粒子的最优解, 进行粒子更新操作. 基本算法是:

$\left\{{\begin{aligned} v_{ki}^{t + 1} =& v_{ki}^t + {c_1} \cdot {r_1}\left( {pbest_{ki}^t - x_{ki}^t} \right)+{c_2} \cdot {r_2}\left( {gbest_{ki}^t - x_{ki}^t} \right)\\ x_{ki}^{t + 1} =& x_{ki}^t + v_{ki}^{t + 1}\end{aligned}}\right.$

上述表述式中, x代表目标所在地点, v代表目标的瞬时速度, pbest为个体最优解, gbest为全局最优解.

2.2 量子遗传算法简介 2.2.1 量子遗传算法原理^[13]

量子遗传算法中, 主要引入了量子位(或量子比特)和量子叠加态两个概念. 在量子计算中, 量子位为最小的信息单位. 一个量子位可以用三种状态来表示, 即0态, 1态和 $\left| 0 \right\rangle $ 和 $\left| 1 \right\rangle $ 之间的任意叠加态. 其状态如下描述:

$\left| \phi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle $

其中, α, β为量子位对应态的概率幅, 量子被观测为 $\left| 0 \right\rangle $ 态的概率用 ${\left| \alpha \right|^2}$ 表示, 被观测为 $\left| 1 \right\rangle $ 态的概率为 ${\left| \beta \right|^2}$ , 需要满足归一化条件 ${\left| \alpha \right|^2} + {\left| \beta \right|^2} = 1$ .

2.2.2 量子门

目前量子门已经有很多种, 有量子非门, 量子受控非门, Hadamard门, 量子旋转门等. 按照量子遗传算法的计算特点, 选择量子旋转门作为更新方式较为适合. 旋转门的的表达式如下:

$U = \left[ {\begin{array}{*{20}{c}}{\cos {\theta _{{{ki}}}}\; - \sin {\theta _{ki}}}\\{\sin {\theta _{ki}}\;\;\cos {\theta _{ki}}}\end{array}} \right]$

通过量子门的变换矩阵可以实现种群更新, 更新过程如下:

$\left| {\begin{array}{*{20}{c}}{\alpha _{ki}'}\\{\beta _{ki}'}\end{array}} \right| = \left[ {\begin{array}{*{20}{c}}{\cos {\theta _{ki}}\; - \sin {\theta _{ki}}}\\{\sin {\theta _{ki}}\;\;\cos {\theta _{ki}}}\end{array}} \right] \cdot \left| {\begin{array}{*{20}{c}}{{\alpha _{ki}}}\\{{\beta _{ki}}}\end{array}} \right|$

θ_ki是旋转角, 其大小和对应的符号由设计的调整策略确定.

2.3 混合粒子群算法设计

将粒子群算法的速度更新方式引入到量子遗传算法, 利用量子遗传算法的量子比特编码染色体^[14], 量子位对应的概率幅代表一个粒子的解, 采用量子旋转门的变换实现种群的更新, 同时利用粒子群算法的速度更新方式来调整量子门的旋转角. 每个染色体占据两个位置, 同时加入量子交叉, 量子变异等遗传算子, 提高了粒子群体的多样性, 避免算法陷进局部最优.

2.3.1 停站方案编码

量子位的概率幅代表一趟列车在该站停与不停的概率, 因此列车停站方案编码采用式(7)的编码方式. 假设路网中存在n个车站, 列车集合 $T = \left\{ {{t_{{k}}}|{{k}} = 1,2, \cdots ,K} \right\}$ , 得到停站方案的染色体表达机制如式(7).

${{{t}}_k} = \left( {\left. {\begin{array}{*{20}{c}}{{\alpha _{k1}}}\\{{\beta _{k1}}}\end{array}} \right|\left. {\begin{array}{*{20}{c}}{{\alpha _{k2}}}\\{{\beta _{k2}}}\end{array}} \right|\left. {\begin{array}{*{20}{c}} \cdots \\ \cdots \end{array}} \right|\left. {\begin{array}{*{20}{c}}{{\alpha _{kn}}}\\{{\beta _{kn}}}\end{array}} \right|} \right)$

(7)

该染色体基因数为列车路过车站的个数, 即染色体含有n个量子比特位, 代表某列车停站方案的一个可行解. 根据量子遗传算法的一般方法, 基因位的初始概率幅 $\left( {\alpha ,\beta } \right)$ 取值都为 $\left( {1/\sqrt 2 ,1/\sqrt 2 } \right)$ , 使其在所有可行解中有相同的取值概率^[15].

2.3.2 粒子群更新方式

粒子群算法的速度更新公式来更新量子旋转门的旋转角, 旋转角更新如下:

$\begin{aligned}{}{\theta _{ki}}(t + 1) = & \omega {\theta _{ki}}\left( t \right) + {r_1}{c_1}\left( {{\theta _{pki}}(t) - \theta (t)} \right) \\ & + {r_2}{c_1}\left( {{\theta _{gki}}(t) - {\theta _{ki}}(t)} \right)\end{aligned}$

(8)

${\theta _{pki}}$ 表示个体最优旋转角, ${\theta _{{\rm{g}}ki}}$ 表示全局最优旋转角, ω表示惯性权重, 采用如下的递减函数^[16]:

$\omega = \omega \_\max - \left( {\omega \_\max - \omega \_\min } \right)\times i/n$

ω使算法随着迭代次数的增加全局搜索能力逐渐降低而局部搜索能力逐步增强. i为当前迭代次数, n为粒子群大小; c₁为学习因子. $c_1 = 1 + iter/n$ , r₁和r₂为[0, 1]之间的随数, ${{i}} = 1,2, \cdots ,N$ , $k = 1,2, \cdots ,K$ , K为粒子数. 更新后的粒子形式如下:

$\left[ {\begin{array}{*{20}{c}}{\alpha _{{\rm{ki}}}^{t + 1}}\\{\beta _{ki}^{t + 1}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\cos {\theta _{ki}}} & { - \sin {\theta _{ki}}}\\{\sin {\theta _{ki}}} & {\cos {\theta _{ki}}}\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}{\alpha _{ki}^t}\\{\beta _{ki}^t}\end{array}} \right]$

(9)

旋转角正负会影响旋转门方向, 因此首先设计好调整方针. θ值过大, 会导致早熟; 反之则会不易收敛. 通常取 $\theta \in \left[ {0.001{{\times}}\pi ,0.05{{\times}}\pi } \right]$ .

直接利用粒子群算法的位置更新公式来动态调整量子门旋转角度的大小和方向. 采用这种方式主要是: (1) 减少参数的数目, 简化算法; (2) 更新方程具有记忆能力, 不仅可以向粒子自身的局部最优信息学习, 也可以向社会的全局最优信息学习, 并且使用ω使得全局和局部搜索能力得到平衡, 加快收敛速度.

2.3.3 混合粒子群算法流程

QGA_PSO求解铁路列车停站方案模型的具体步骤如下所示:

1) 确定粒子群算法的基本参数, 如群体规模, 粒子长度等. 将所有染色体的量子比特 $\left[ {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right]$ 初始化为 $\left( {1/\sqrt 2 ,1/\sqrt 2 } \right)$ ;

2) 按照前文染色体编码方式随机生成初始粒子pop. 当前迭代次数 $n \leftarrow 1$ ;

3) 计算每个粒子各自对应的目标函数的值, 并记下最优个体及其对应的适应度值;

4) 进行迭代判断, 当满足给定的停止条件时退出, 否则继续步骤5);

5) 利用式(8)更新θ;

6) 计算当前各粒子所对应的各目标函数值, 当粒子的目标函数值大于前一次的值时, 更新粒子, 否则粒子保持不变;

7) 根据交叉概率, 对粒子进行一致性交叉概率, 对粒子进行一致性交叉操作;

8) 根据变异概率, 对种群进行变异操作;

9) 记下最优个体及其对应的适应度值;

10) 根据概率函数 $si{g_{{{ki}}}} = \displaystyle\frac{1}{{1 + {e^{ - \cos ({\theta _{ki}})}}}}$ 求问题的解空间. 当 $rand() < si{g_{{{ki}}}}$ 时, ${x_{{{ki}}}} = 1$ ; 否则 ${x_{ki}} = 0$ ;

11) 迭代次数t=t+1, 返回步骤4).

2.3.4 算法分析

将算法应用于离散多目标的ZDT1函数优化问题, 以验证算法的适用性. ZDT1函数在两个目标函数上的最优值分别为0和1.首先随机设置种群规模为50, 迭代次数100, 固变异概率pm, 对于不同的量子交叉概率pc, 得到的性能对比表如下:

从结果可以看出, 当pc很小时, 收敛性交叉, 随着pc的增大, 交叉作用促使个体向最优解进化. 当pc=0.8时算法得到最好的收敛性. 当pc超过0.9时, 群体多样性降低, 个体易收敛于局部最优解.

然后固定量子交叉概率为0.8, 针对不同的pm取值得到的性能对比见表2.

同样, 适当增加变异概率能使个体收敛到最优值, 取pm=0.08.

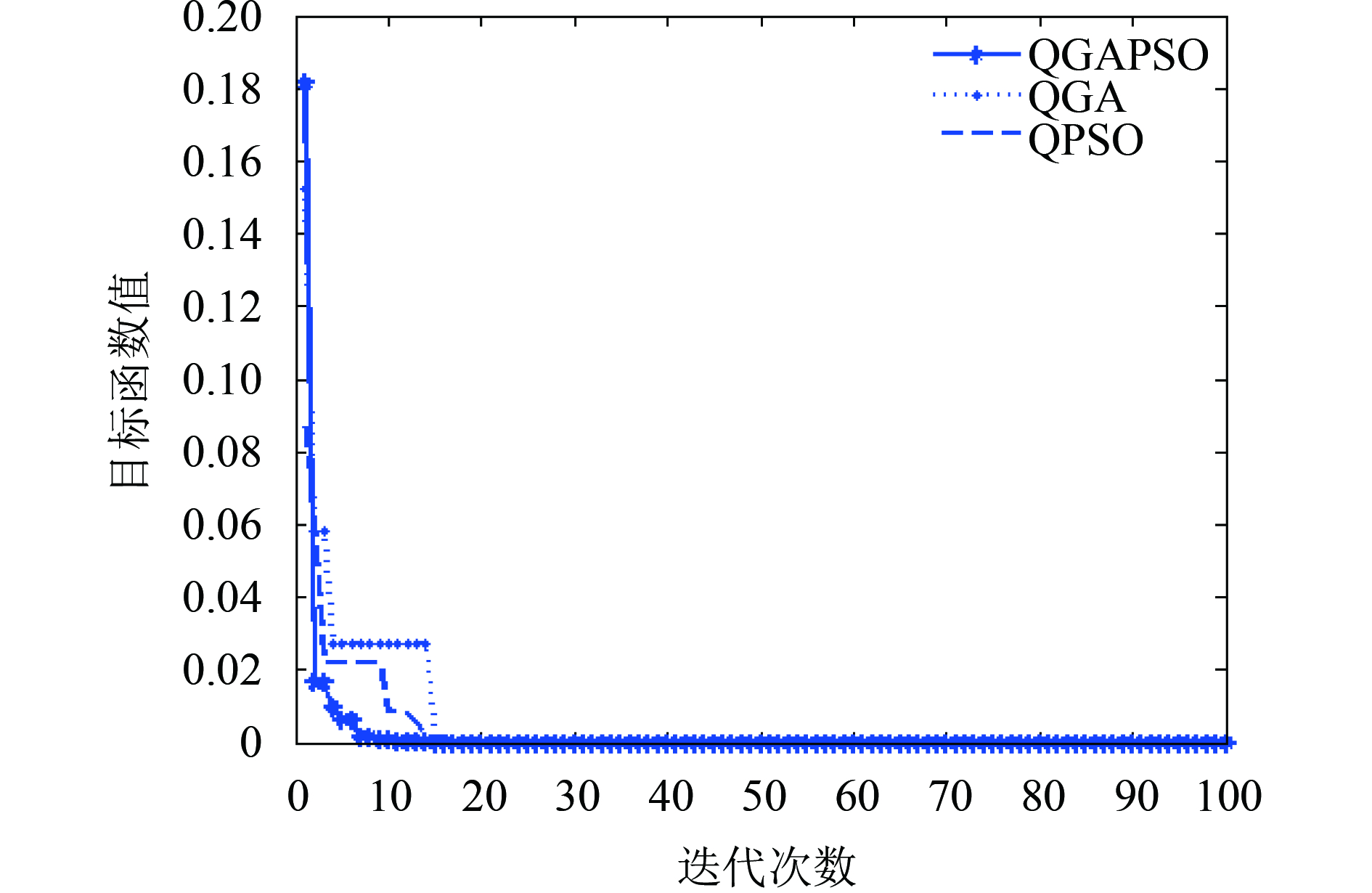
接下来将改进算法与量子遗传算法(QGA)以及量子粒子群算法作对比, 得到各算法在两个目标函数上的取值如图1和图2所示.

由上图可知, QGA_PSO算法能以较快速度收敛于最优解. 相比其余两种算法, 其在收敛算法和算法精度上都有相应的提高, 证明了本文算法的有效性.

3 实例验证和结果分析

采用2015年12月1日某区段客流进行验证. 全路运行图开行24列速度为300 km/h的下行列车.

3.1 数据准备 3.1.1 客运站点等级划分

车站等级是影响列车停站方案的一个关键因素, 因此有必要对经过的车站进行车站等级划分. 本文采用文献[17]提出的灰色关联度分析方法得到各车站的等级系数, 为列车停站方案的区段可达性计算奠定基础. 各车站等级系数如表3所示.

3.1.2 列车开行对数

以某区段2015年12月1日OD客流为依据进行分析. 对于某一开行区段列车停站方式主要包括4种: (1) 开行直达列车; (2) 开行大站停列车; (3) 开行大站套小站的列车; (4) 开行站站停列车. 考虑到本文主要是优化高速铁路列车的开行方案, 为了保证旅客旅行速度, 不开行站站停列车. 计算各类停站方案旅客列车开行方案时, 需要已知不同停站方案列车吸引客流的比例, 以此比例将OD客流分配到不同停站列车上去, 本文采用文献[18]的站间客流吸引比例来分担客流. 根据各等级车吸引站间客流的比例以及OD客流数据, 得到总共开行21列列车, 其中直达列车4列, 大站停列车6列, 择站停列车11列.

3.2 列车停站方案求解

粒子群参数设置: 结合问题规模及第2节中的分析, 设置种群大小50, 粒子维数11(车站数), 迭代次数100, 交叉概率0.8, 变异概率0.08, 车站等级系数, 车站客流量等. 利用Matlab7.0软件编程进行计算得到列车停站方案, 迭代10次达到稳定值. 原停站方案列车开行24列, 中间总停站43次, 优化后的停站方案列车开行21列车, 中间总停站28次, 相对于以前的停站方案, 优化后的停站方案在满足客流量的基础上减少了列车开行对数及停站次数, 使得旅客的旅行时间减少了, 同时减少了的铁路部门的开行费用. 如图3所示为优化后的列车停站方案示意图.

3.3 算法性能对比

为了验证本文算法的有效性, 将本算法与文献[15]和文献[19]从运行时间, 目标函数及解的多样性进行对比.

(1) 三种算法运行时间对比见表4.

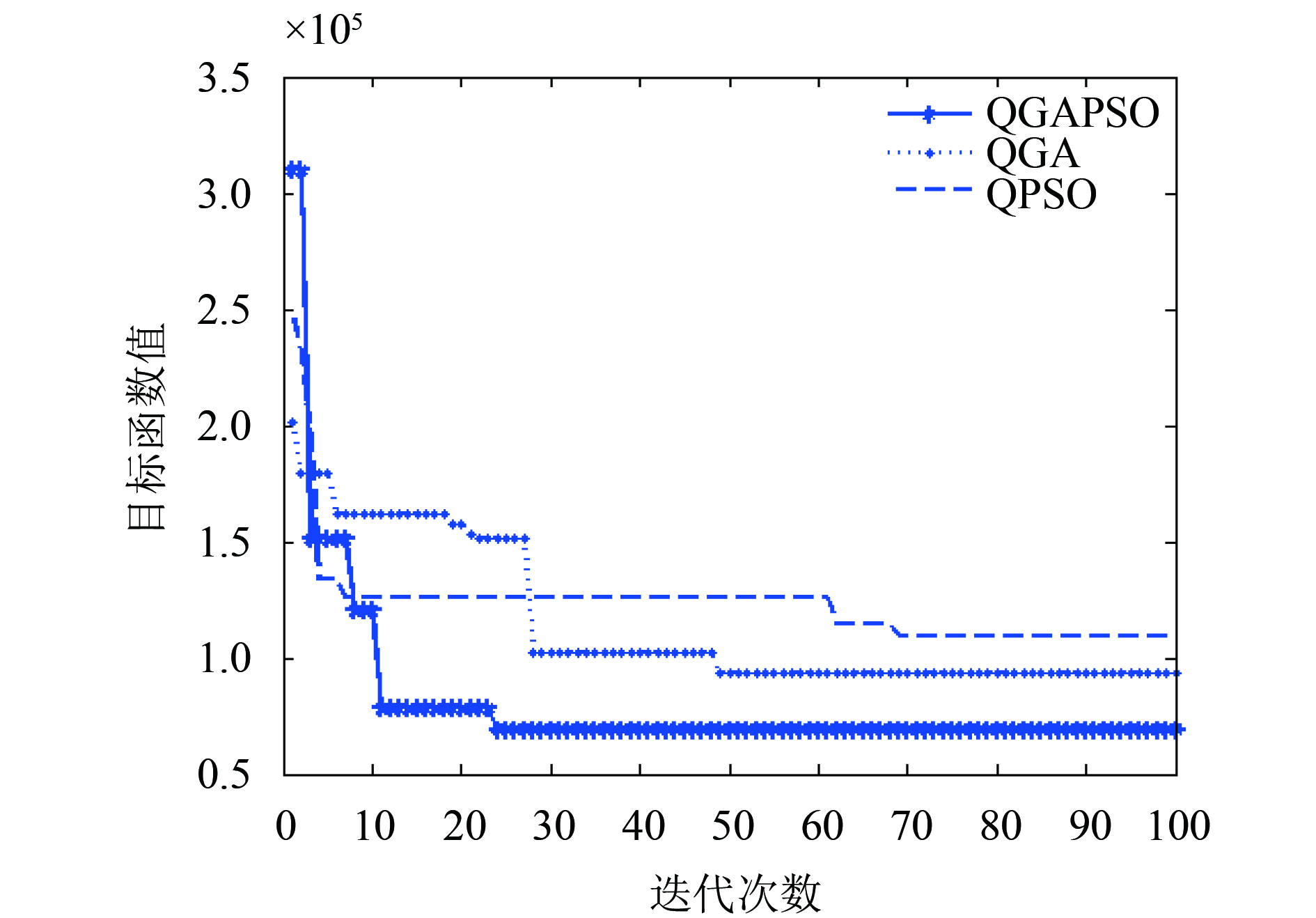
(2) 三种算法在目标函数方面的比较可由表4及图4分析得知. 改进后的算法运行时间更短, 区段可达性也有相应的提高, 目标函数收敛更快, 大约在迭代15次的时候就收敛了, 量子遗传算法和离散量子粒子群算法在迭代到50次以后才收敛, 且收敛后的目标函数值未到最小. 可见, 改进后的算法效率更高.

(3) 为能更好的评价本文中停站方案解的多样性, 在此定义多样性为某一列车的停站方案与其余列车停站方案的差异. 因为停站方案的解为0或1的二进制, 因此多样性为不同解之间的汉明距离, 即 $MD = \sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = i + 1}^m {d\left| {{x_i} - {x_j}} \right|} } $ .

由上式计算出3种算法的多样性对比如表5所示.

由表5知改进后的算法在多样性上比BQPSO有的明显的提高, 但是和QGA相比, 多样性没有明显的优势. 这是因为本文的编码方式和QGA的编码方式相同.

4 总结

基于粒子群算法存在易陷入局部最优, 不适用于离散空间等缺点, 本文将量子遗传算法引入到粒子群算法中, 提出了改进的量子遗传粒子群算法(QGA_PSO). 算法首先将染色体编码为量子比特的形式, 每个染色体表示粒子的两个位置, 减少粒子种群的大小; 其次, 根据标准PSO的速度更新公式, 更新量子旋转门的角度, 加快收敛速度, 同时引入量子交叉和量子变异增加群体多样性. 算例仿真表明, 提出的QGA_PASO相对于QGA, BQPSO能在更短时间内收敛, 且得到的停站方案在满足旅客量的基础上使得旅客旅行时间缩短同时减少铁路企业开行列车费用, 对铁路客运管理部门有一定的指导作用.