随着人们生活水平的提高, 汽车得到了越来越多的普及. 车辆增多引发的车祸事故驱使消费者对汽车的安全性越来越重视, 后视镜作为提供车辆视野安全的主要安全工具就显的尤为重要, 后视镜使驾驶员在驾驶中能够观察汽车两侧以及后方的交通状况, 是保障行车安全必不可少的装置. 一般来说, 汽车的后视镜需要有良好的视野范围, 以便驾驶员能够全面地了解车后方的道路情况. 同时, 后视镜也要使图像的畸变尽可能小, 以使驾驶员能够准确地判断距离. 正常的驾驶员在仅转动眼球而不回头的情况下, 约可以看到前方200°左右的范围, 换句话说, 还有160°是看不见的. 虽然普通的左右后视镜加中央后视镜, 还可以提供约60°左右的可视范围, 然而剩下的那些死角盲区却成为了大多数车祸发生的直接因素. 当前市场上有很多不同规格的后视镜, 它们各有优缺点. 如何建立相关的数学模型, 对外后视镜的镜面曲面外形和分界示意线的位置进行优化, 使其兼顾平面镜和凸透镜的优点, 是当前需要解决的主要问题. 本文通过Matlab计算与仿真后得知当曲率为1151 mm时, 可视角度为80°, 可视区域变大且图像清晰度较高. 根据几何光学公式得知当分界线的位置处于后视镜外侧约1/3处时驾驶员能获得满意的视野.
1 后视镜分析 1.1 曲面镜外形通过模型的建立, 主要完成对镜面的曲面外形以及分界示意线的位置的优化. 由于双曲面镜有镜面组合出现变形和平面镜向变曲面镜过渡时造成眩晕的缺点, 所以优化镜面曲面外形时需要考虑以下因素[1]:
(1) 如何通过简单、便利、低成本的方式缓解眩晕.
(2) 如何改变凸透镜曲率半径的大小, 实现平面镜与凸面镜的平滑过渡, 同时降低失真率.
1.2 分界示意线的位置要求为了保证外后视镜能够扩大可视角, 减小盲区, 在确立分界线的位置时, 需考虑以下因素[2]:
(1) 左后视镜安全区域: 至少看到向左宽2500 mm区域, 并从驾驶员眼点后10 000 mm外延伸至地面;
(2) 右后视镜安全区域: 至少看到向右宽4000 mm区域, 并从驾驶员眼点后20 000 mm外延伸至地面;
由于后视镜外侧凸透镜(副视野区域)存在部分失真, 所以设计时应该保证凸透镜与平面镜分界处以内(即平面镜主视野区域)满足上述安全视野区域, 以能够实现视野观察和距离判断[3], 保证驾车安全.
2 基于三角基线性拟合算法模型的建立与求解 2.1 后视镜曲面外形1) 盲区的产生
假设人体模型为H, 测量内后视镜的后视野时[4], 眼相对人的坐标:
| $\begin{array}{l}X = - 185.01472 + 10.281641\alpha - 0.032032{\alpha ^2}\\{Y_{{\text{左}}}}{\rm{ = - }}72.5\\Z = 662.11757 + 0.398747\alpha - 0.059301{\alpha ^2}\end{array}$ | (1) |
测量外后视镜的后视野时, 眼相对人的坐标:
| $\begin{array}{l}X = - 185.01472 + 10.281641{a^2}\\{Y_{{\text{左}}}}{\rm{ = - }}1.5,\,{\kern 1pt} \quad {Y_{{\text{右}}}}{\rm{ = }}63.5\\Z{\rm{ = }}662.11757{\rm{ + }}0.398747\alpha {\rm{ - }}0.059301{\alpha ^2}\end{array}$ | (2) |
式(1)、(2)中
2) 后视镜视角的计算
驾驶盲区示意图如图1所示. 驾驶根据反射定理, 可以得知视角表达式[5]:
| $\begin{gathered}\theta {\rm{ = }}2\left( {2\alpha {\rm{ + }}\beta } \right) \\\alpha {\rm{ = }}{\tan ^{ - 1}}\frac{\omega }{{2r}};\;\beta = {\tan ^{ - 1}}\frac{\omega }{{2s}} \\\end{gathered} $ | (3) |
式(3)中
| $\theta = 2\left[ {2{{\tan }^{ - 1}}\frac{\omega }{{2r}} + {{\tan }^{ - 1}}\frac{\omega }{{2s}}} \right]$ | (4) |
| $\lambda = \frac{1}{2}{\tan ^{ - 1}}\frac{{{s_t}}}{{{s_1}}}$ | (5) |
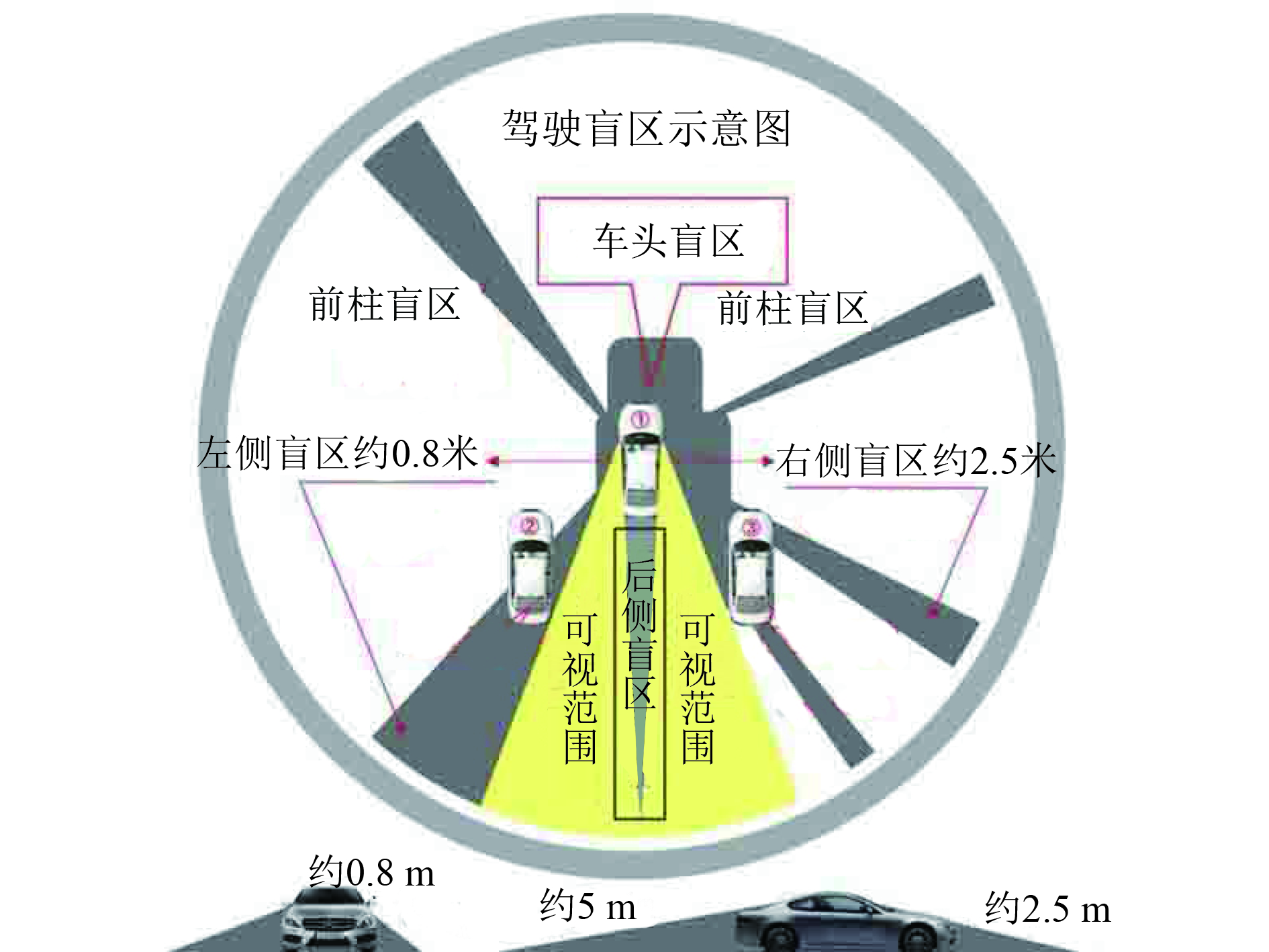
|
图 1 驾驶盲区示意图 |
镜面宽度取不同值时, 眼睛到后视镜的距离计算结果如表1所示. 双目视角的计算结果如表2所示.
| 表 1 眼睛到后视镜距离 |
| 表 2 双目视角 |
3) 模型的建立
使用三角基线性拟合方法建立一种新的曲面拟合方法[6], 即三角基最佳逼近方法, 与最小二乘法相比, 三角基线性拟合法有两个较大的改进.
① 建立的拟合函数由系数向量构成, 系数向量是空间坐标的函数, 从而使拟合函数在不同位置有不同的形式, 精度更高.
② 对大量的离散数据, 不需要进行分块拟合和平滑化, 某点处的数值只受影响区域内节点影响, 影响区域外的节点对数值没有影响, 因而具有紧支性.
4) 模型的求解
实际测量后视镜, 测量区域为:
| $\Omega :\left\{ {{x_1}} \right. \le x \le {x_m},{y_1} \le y \le \left. {{y_n}} \right\}$ | (6) |
在测量区域上选取
| ${x_i} = {x_i}_{ - 1} + \frac{{{x_m} - {x_1}}}{m},{y_j} = {y_{j - 1}} + \frac{{{y_n} - {y_i}}}{n}$ | (7) |
根据三角基线拟合法, 对二次曲面进行网格化, 得到网点的模型为:
| $\begin{array}{l}z = f\left( {\left. {x,y} \right)} \right. \\\;\;\;=\left( {\left. {{a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3}} \right)} \right. \times \left( {\left. {{b_0} + {b_1}y + {b_2}{y^2} + {b_3}{y^3}} \right)} \right.\end{array}$ | (8) |
式(8)中ai, bj为系数, i, j=0, 1, 2, 3.
实际计算时为防止溢出,
| $\left\{ \begin{gathered}{{x'}_i} = {x_i} - \bar x \\{{y'}_j} = {y_j} - \bar y \\\end{gathered} \right.$ | (9) |
式中,
| $\begin{array}{l}f\left( {x,y} \right) = \left[ {{a_0} + {a_1}\left( {x - \bar x} \right) + {a_2}{{\left( {x - \bar x} \right)}^2} + {a_3}{{\left( {x - \bar x} \right)}^3}} \right] \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \left[ {{b_0} + {b_1}\left( {y - \bar y} \right) + {b_2}{{\left( {y - \bar y} \right)}^2} + {b_3}{{\left( {y - \bar y} \right)}^3}} \right]\end{array}$ | (10) |
为验证本文方法的有效性, 对某后视镜进行了拟合. 网格化得测量区域
| $\left\{ {10 \le x \le 250,6.5 \le y \le 246.5} \right\},$ |
在其测量区域上选取
| $\begin{array}{l}f\left( {x,y} \right) = 47.582 - \left({1281.61 + 0.052855 \times {{\left( {x - \bar x} \right)}^2}}\right. \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {+ 0.088453 \times {{\left( {y - \bar y} \right)}^2}}\right)^{1/2} \end{array} $ | (11) |
在拟合曲面上通过数值实验的办法确定主视野区, 使从眼点出发的光线通过主视野区镜面反射后, 在测试屏上能照射到国标规定的区域[7].
以主视野区曲面的边界为边界约束, 用运自适应普适无网络格法解特征方程:
| $\frac{{{{\left( {1 + {{z'}_x}^2} \right)}^{3/2}}}}{{\left| {{{z''}_{xx}}} \right|}} + \frac{{{{\left( {1 + {{z'}_y}^2} \right)}^{3/2}}}}{{\left| {{{z''}_{yy}}} \right|}} = 2r$ | (12) |
式(12)中, r≥500.
可得副视野区的曲面方程, 它和主视野区的曲面是分片光滑的连续曲面(在连续接线处连续但无连续偏导数).
5) 曲率半径的计算
R用mm表示, 计算公式如式(13)、(14)所示.
| ${r_{pi}} = \frac{{{r_i} + r'}}{2}$ | (13) |
| $r = \frac{{{r_{p1}} + {r_{p2}}}}{2}$ | (14) |
式中,
选取P1–P8 8个测试点, 测试结果如表3所示. 计算出8个点处的曲率半径如表4所示.
| 表 3 测试结果数据显示 |
| 表 4 8个点处的曲率半径 |
在第一测点的曲率半径:
| ${R_1} = \frac{{{r_{p1}} + {r_{p2}}}}{2} = \frac{{1121.535 + 1132.755}}{2} = 1127.145$ | (15) |
在第二测点的曲率半径:
| ${R_2} = \frac{{{r_{p3}} + {r_{p4}}}}{2} = \frac{{1142.38 + 1162.455}}{2} = 1152.4175$ | (16) |
在第三测点的曲率半径:
| ${R_3} = \frac{{{r_{p5}} + {r_{p6}}}}{2} = \frac{{1136.235 + 1161.77}}{2} = 1149.0025$ | (17) |
在第四测点的曲率半径:
| ${R_4} = \frac{{{r_{p7}} + {r_{p8}}}}{2} = \frac{{1200.84 + 1156.45}}{2} = 1178.645$ | (18) |
最终得到这种后视镜的曲率半径:
| $R = \frac{{{R_1} + {R_2} + {R_3} + {R_4}}}{4} = 1151.8025$ | (19) |
所以:
在主视野区域在安全视野的条件下, 通过减小副视野区镜面的曲率半径, 从而使得可视角度增大. 通过Matlab计算与仿真后得知当曲率为1151 mm时, 可视角度为80°,可视区域变大且图像清晰度较高, 使用前和使用后广角范围对比如图2所示.
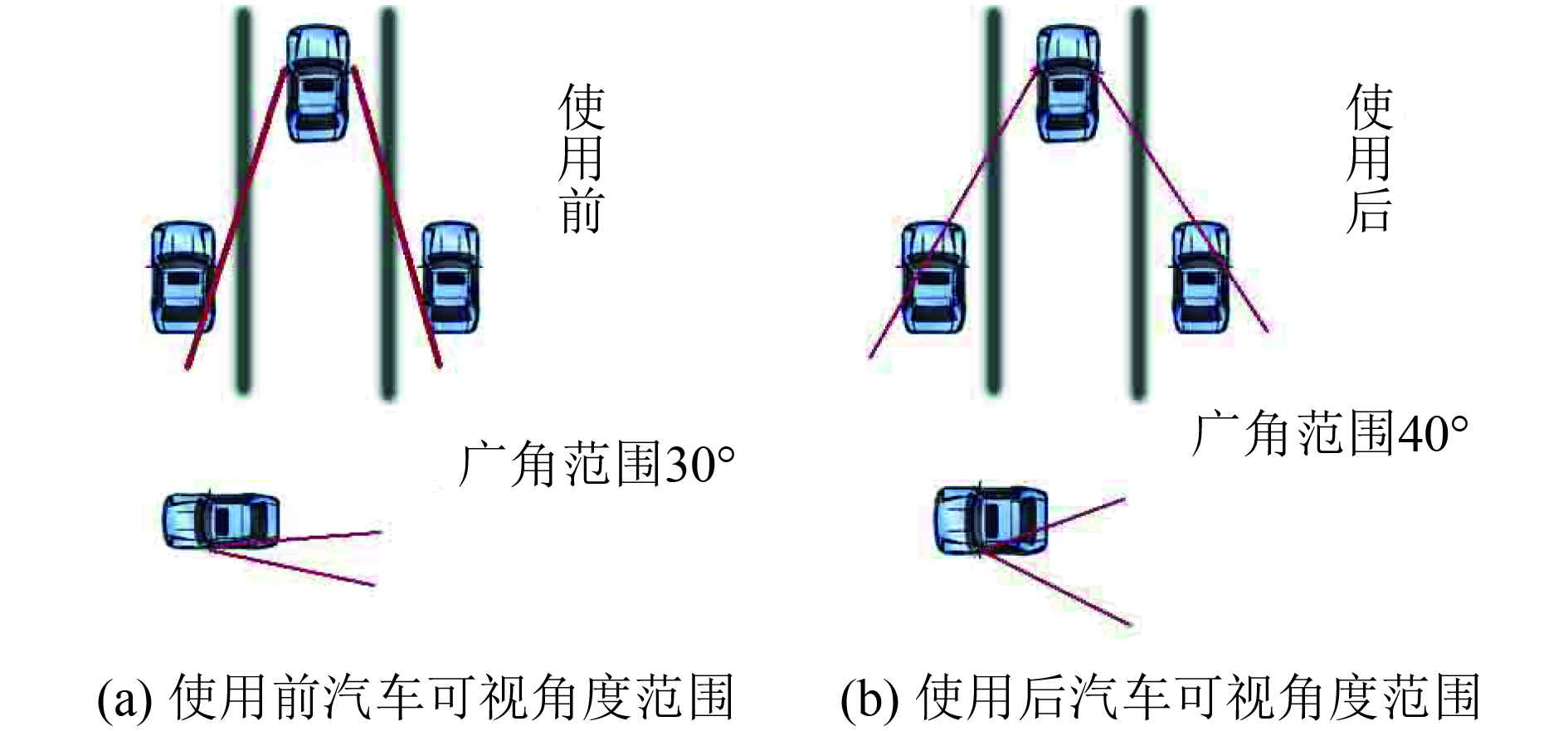
|
图 2 广角范围 |
2.2 分界示意线
针对四种曲率半径不同的后视镜分成像清晰, 一般可选取实用的最佳角
| ${L_{af}} = \frac{{A'B'}}{{2{\rm {tg}}{\beta _{af}}/2}} - V = \frac{{A'B'}}{{2{\rm {tg}}20'}} - V$ | (20) |
由式(20)可知, 当物体的高度和物距一定时, 镜面的曲率半径越小, 映像的高度也就越小, 为了看清映像, 就要相应地减小
根据光在凸透镜上折射和反射的原理, 以及光经过凸面镜反射后空间成像的原理, 可由方程组(21)计算后视镜曲率半径
| $\left\{ \begin{array}{l}m = V/u\\1/u + 1/V = 2/R\end{array} \right.$ | (21) |
确定镜面长度时, 应考虑车体高度和镜面到后轮胎前缘的距离, 这主要因为后轮是肇事的危险区, 因此必须清晰可见. 后轮到镜面的距离一般为3~7米[9], 如果此处的景物在镜面里可以完全看到, 再考虑车体的高度, 整个镜面里就能得到30米处景物的映像. 在选定镜面得曲率半径R之后, 可利用几何光学原理求出镜面的长度
| $a = AB \cdot R/\left( {R + u} \right)$ | (22) |
在确定镜面的宽度时, 也可以利用式(22)计算. 此时的
根据成像原理来确定
| $\frac{1}{u} + \frac{1}{v} = \frac{1}{f} = \frac{2}{r},\;\frac{{h'}}{h} = \frac{{R - v}}{{R + u}}$ | (23) |
式(23)中:
设
| $W = {\rm arctg} \frac{{h'}}{{d + v}}$ | (24) |
对曲率半径R=1151 mm的凸面镜的数据测试结果如表5所示. 另外, 根据镜面的面积进行逆运算, 求出能够满足视野要求的分界线位置. 也就是说, 镜面分界线的位置一定要与它的曲率半径保持一定比例的匹配关系[10]. 由于驾驶员的身材、坐姿及驾驶习惯存在差异, 为保证驾驶员能获得满意的视野, 将分界线的位置处于后视镜外侧约1/3处是最优比例, 此比例下呈现的映像稍小.
3 仿真结果采用三角基线性拟合法对后视镜仿真曲面拟合后, 结果如图3所示, 可以看到拟合之后后视镜图形拟合曲面的峰谷的个数不随节点值变化, 凹凸性相对稳定, 比用最小二乘法拟合的曲面相对平滑. 针对后视镜的缺陷, 分别取5 m到10 m的客车, 10 m到15 m, 15 m到20 m的3种类型客车, 根据几何光学公式对镜面的面积进行逆运算, 可以求知不同的车型的合适镜片尺寸. 然后对后视镜建立曲面拟合模型, 通过三角基线性拟合算法对复杂的曲面进行拟合, 在副视野区域图像的失真率不大于且主视野区域在安全视野的条件下, 通过减小副视野区镜面的曲率半径, 从而使得可视角度增大, 进而实现后视镜的曲面外形优化.
| 表 5 曲率半径R=1151 mm时的测量数据 |

|
图 3 三角基线性matlab拟合结果 |
4 结束语
本文根据几何光学公式对镜面的面积进行逆运算, 可以求知不同的车型的合适镜片尺寸. 然后对后视镜建立曲面拟合模型, 通过三角基线性拟合算法对复杂的曲面进行拟合, 在副视野区域图像的失真率不大于且主视野区域在安全视野的条件下, 通过减小副视野区镜面的曲率半径, 从而使得可视角度增大. 进而实现后视镜的曲面外形优化.
本文所建立的模型, 使用范围相对较广, 曲面拟合法可以解决很多实际的工程问题, 比如采用曲面拟合法来检测高温区域的边缘, 根据获取的目标表面温度图像, 进行高温域检测. 曲面拟合法可克服插值法的不足之处, 近似地求出变量与目标函数关系, 用于设备在线检测及故障诊断中的应用则集中于传感器、信息融合技术等方面的分析.
| [1] |
曹竞辉, 孙贵斌, 王耀, 等. 汽车后视镜盲区的解决方案及控制策略. 机电技术, 2016(4): 80-82. |
| [2] |
周博. 汽车外后视镜镜片尺寸及位置设计. 上海汽车, 2015(12): 41-44. |
| [3] |
牛慧超, 王卫华, 白洁. 汽车后视镜视野检测的智能仿真算法. 地理与地理信息科学, 2009, 25(6): 110-111. |
| [4] |
李莉莉. 汽车后视镜曲率半径测控系统的设计与实现[硕士学位论文]. 武汉: 武汉理工大学, 2014.
|
| [5] |
李海燕, 谭光宇, 李海宝, 等. 基于逆向工程的汽车后视镜再设计研究. 机床与液压, 2009, 37(6): 29-31. |
| [6] |
王卫华, 李昆. 曲面拟合技术在汽车后视镜理论建模中的应用. 武汉理工大学学报, 2005, 27(11): 106-109. DOI:10.3321/j.issn:1671-4431.2005.11.032 |
| [7] |
熊玉洁. 后视镜布置与设计. 轻型汽车技术, 2004(11): 8-12. |
| [8] |
陈浩, 马艳, 郝亮, 等. 汽车驾驶员视野拓展系统的设计与实现. 汽车工程师, 2016(6): 19-23. |
| [9] |
欧春烃. 汽车后视镜稳健设计及有限元分析[硕士学位论文]. 重庆: 重庆大学, 2016.
|
| [10] |
许晓杰, 潘秋菱, 王昌银, 等. 汽车后视镜反射率测量系统的研究. 光电子•激光, 2005, 16(5): 634-636. |
 2018, Vol. 27
2018, Vol. 27


