运动捕捉(Motion Capture, MOCAP)是一种获取真实运动数据的技术, 指通过传感设备记录人体在三维空间中的运动轨迹, 并将其转化为抽象的运动数据, 最后根据这些数据驱动物体或者虚拟人体运动的技术. 随着虚拟现实技术的飞速发展, MOCAP已经广泛地应用于各个领域, 例如计算机动画、电脑游戏、影视动画、教育医学、运动分析、体育训练、智能监控、运动仿真等领域. 为了获得精确的数据, 已经有很多MOCAP技术, 其中基于光学传感器的运动捕捉技术是最为流行的技术, 代表性的商业设备有Motion Analysis和Vicon. 但即使是专业的商业运动捕捉设备在捕捉数据时也会存在标记点缺失的情况. 例如, 采集数据时, 标记点被物体或者身体的其他部位遮挡, 或者在光线的不理想都会使得相机不能捕获该标记点, 导致捕捉到的数据有缺失. 为了避免光线对光学传感器的影响, CMU数据库中的数据都是在室内采集到的, 大多只会有个别标记点的缺失, 比较容易恢复. 但有些特别的运动(如撑杆跳高等)需要在特定的室外场地进行数据采集, 此时室外光线的存在导致基于红外光采集信息的设备捕捉标记点运动轨迹时会引起运动轨迹丢失或出现较大偏移. 同时在室外采集时发现当一个标记点缺失时, 其相邻的标记点常常也会缺失, 并且这些缺失会在时间域持续一段时间. 这会导致MOCAP数据的空间域和时间域相关信息都被破坏, 所以失真恢复是MOCAP数据直接应用之前的重要处理步骤, 而由于人体运动的复杂性和多样性又给失真恢复带来了难度.
针对上述标记点缺失的问题, 商业设备常用的算法是插值算法, 这些算法适用处理小规模标记点缺失, 对标记点连续缺失的情况恢复效果较差. 为了提高MOCAP数据的恢复效果, 国内外人员提出了许多恢复方法. 现有的MOCAP数据失真恢复算法可以分为以下3类: 1) 基于信号处理的算法. 包括高斯滤波、DCT变换、傅里叶变换、小波变换、卡尔曼滤波、线性动力系统(LDS)[1–5]. 这些方法只是对每一个标记点进行独立的处理, 忽略了人体结构潜在的相关性, 也就是各标记点的相关性, 在处理简单运动时是很有效的, 但在处理复杂运动时效果欠佳. 2) 基于低秩填充的方法. Lai等[6]首先提出利用人体运动序列的近似低秩性, 将MOCAP失真恢复问题转化为矩阵低秩填充问题, 并用奇异值阈值法(SVT)恢复缺失的数据. Tan等[7]注意到运动轨迹段数据矩阵具有更优良的低秩性, 提出将运动序列重新组织为不同轨迹段的组合进行局部矩阵补全恢复(TSMC), 达到了较好的重构效果. 彭淑娟等[8,9]将运动序列按语义进行分割, 得到不同姿态的运动语义子区间, 再对每个失真运动子片段数据矩阵根据其更优低秩特性进恢复. Feng等[10]进一步提出同时利用运动序列的低秩结构和相邻帧的时域稳定特性来恢复缺失的数据. 但是由于运动序列实际上只是近似低秩, 在利用奇异值阈值法恢复时舍去的较小奇异值必然造成误差, 而这个误差就是低秩填充法理论上的误差下限. 同时, 实际恢复过程中, 当出现数据连续缺失时恢复效果欠佳. 3) 基于数据驱动的方法. 近年来, 得益于新型运动捕捉设备的发展和捕捉技术的提高, MOCAP数据呈现出了爆发性的增长, 为基于数据驱动的算法提供了足够多的样本, 促进了这些算法的改善, 使其能较充分考虑到人体运动的复杂性和多样性. Hou等[11]利用稀疏表示的特性, 根据同一字典下, 每个点轨迹的观测数据和缺失数据具有相同的稀疏表示系数来恢复缺失的数据, 提出了基于轨迹稀疏表示的恢复算法, 充分利用了运动序列的时序特性, 但是没有考虑人体自身的潜在的相关性. 而Xiao等提出的算法(SRMMP)[12]在逐帧恢复的同时, 通过相邻帧和被选取最多的原子来利用帧与帧之间的相关性, 提高了恢复效果. Feng等[13–15]进一步提出了先对数据进行预处理, 再通过重叠窗处理利用帧与帧之间的相关性, 用训练得到的字典来恢复数据. 由于人体的骨骼是刚体, 所以在同一骨骼上的两个标记点之间的距离表示的就是骨骼的长度, 这个长度在整个运动过程中近似常数, 但是, 在用上述方法进行恢复时, 骨骼长度可能会发生变化, 特别是当标记点连续很多帧缺失时, 恢复后的骨骼长度误差较大. Li等[4]首先通过运动数据中未缺失部分建立缺失数据预测概率模型, 接着利用骨骼长度约束对运动数据进行恢复. 由于该方法对同一段的其他标记点的依赖性较高, 因此, 难以进行标记点距离的准确测量. Tan[16]在矩阵填充的基础上利用骨骼长度不变这一约束, 进一步提高了精确度, 但是同样地具有低秩填充的固有近似误差.
上述算法在针对标记点连续缺失的情形时, 都不能同时保持缺失点坐标恢复精度和骨骼长度恢复精度. 综合以上方法的优缺点, 为了同时提高缺失点坐标恢复精度和骨骼长度恢复精度, 本文提出一种基于人体骨骼长度约束和稀疏表示理论的改进算法. 该算法根据MOCAP数据的的特性, 首先对数据进行预处理, 使变换后的数据表示的是相邻标记点的相对位置的变化, 由此得到骨骼长度约束项. 然后在字典训练时, 加入骨骼长度约束项, 使训练得到的字典在重构运动序列时能够保持人体骨骼长度不变的特性. 最后再利用训练得到的字典和骨骼长度约束项, 对失真数据进行恢复. 通过加入骨骼长度约束项, 来提高缺失标记点坐标的恢复精度和运动序列骨骼长度的恢复精度, 便于后续对MOCAP数据的储存和处理.
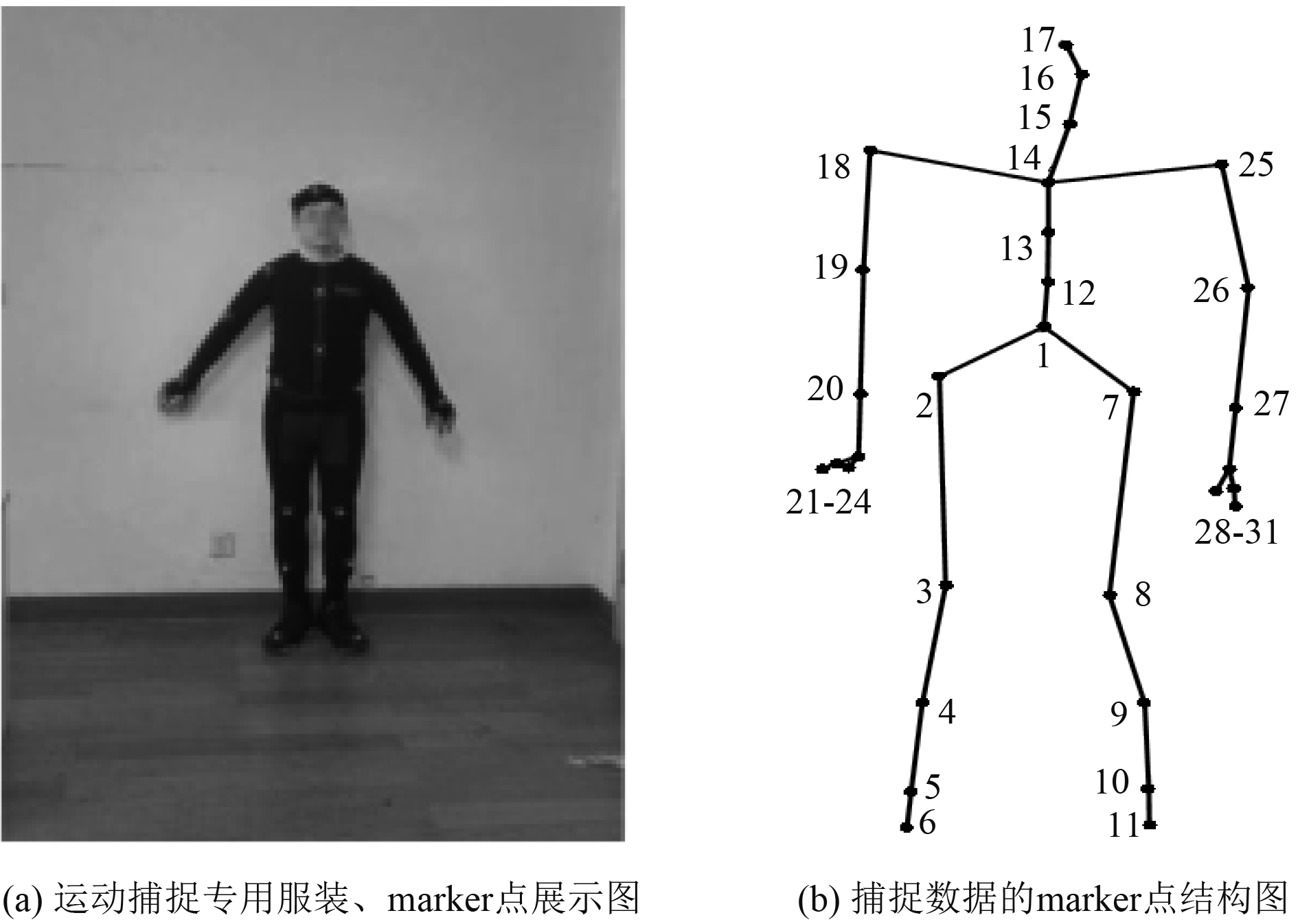
1 数据预处理图1为本实验室采集MOCAP数据所用设备中的运动捕捉专用服装、marker点展示图和CMU数据库(http://mocap.cs.cmu.edu/)中的marker点拓扑图. 人体运动捕捉数据主要记录的是人体骨架标记点的空间位置及其运动轨迹信息, 通常运动捕捉数据直接得到的是标记点在世界坐标系下的三维坐标. 而后续的存储(如vicon)一般是通过储存每个标记的平移和旋转信息来储存数据, 其中的旋转信息通过欧拉角表示. 这些反映坐标变化的数据存储在AMC文件中, 而一些不变的数据, 如标记点的初始位置, 自由度和骨骼长度单独储存在ASF文件中, 这样的存储方式无疑避免了数据冗余. 通过AMC和ASF文件能够解析出MOCAP数据在世界坐标系下的表示, 从而能够利用和编辑MOCAP数据.
|
图 1 运动捕捉设备和捕捉数据展示图 |
通过以上分析可知保持MOCAP数据中骨骼长度信息不变对后续的存储至关重要, 同样, 在编辑和利用MOCAP数据时保持骨骼长度不变也非常重要, 否则会使创造出的人体模型发生畸变. 由于在世界坐标系表示下的MOCAP数据, 其坐标数值是复杂多变的, 即使是相似的运动, 在用世界坐标系表示时, 其相应的各标记点的三维坐标值可能也会有很大的差异, 对此, Feng等[13–15]提出坐标标准化法和按人体不同部位将数据分别处理的方法. 其中坐标标准化方法是通过平移和旋转变换将各标记点的坐标都转化为相对于Root点的局部坐标, 这样的坐标表示更能体现各运动数据的相似性.
1.1 坐标标准化基于以上的MOCAP数据的特性和要求, 本文对原始世界坐标系下的MOCAP数据X进行变换. 和Feng等[13–15]有所不同, 本文将各标记点标在原始世界坐标系下的坐标转化为表示相邻标记点坐标差的局部坐标. 同一骨骼上两个标记点的相对距离表示的就是人体骨骼长度, 但因不同人的骨骼长度很可能不相等, 从而导致即使同一运动路径、同一运动方式产生的标准化坐标也会产生差异, 在字典训练时会使同一类运动的样本间差异性很大. 所以要先对运动序列进行骨骼长度标准化处理. 具体算法如下[17].
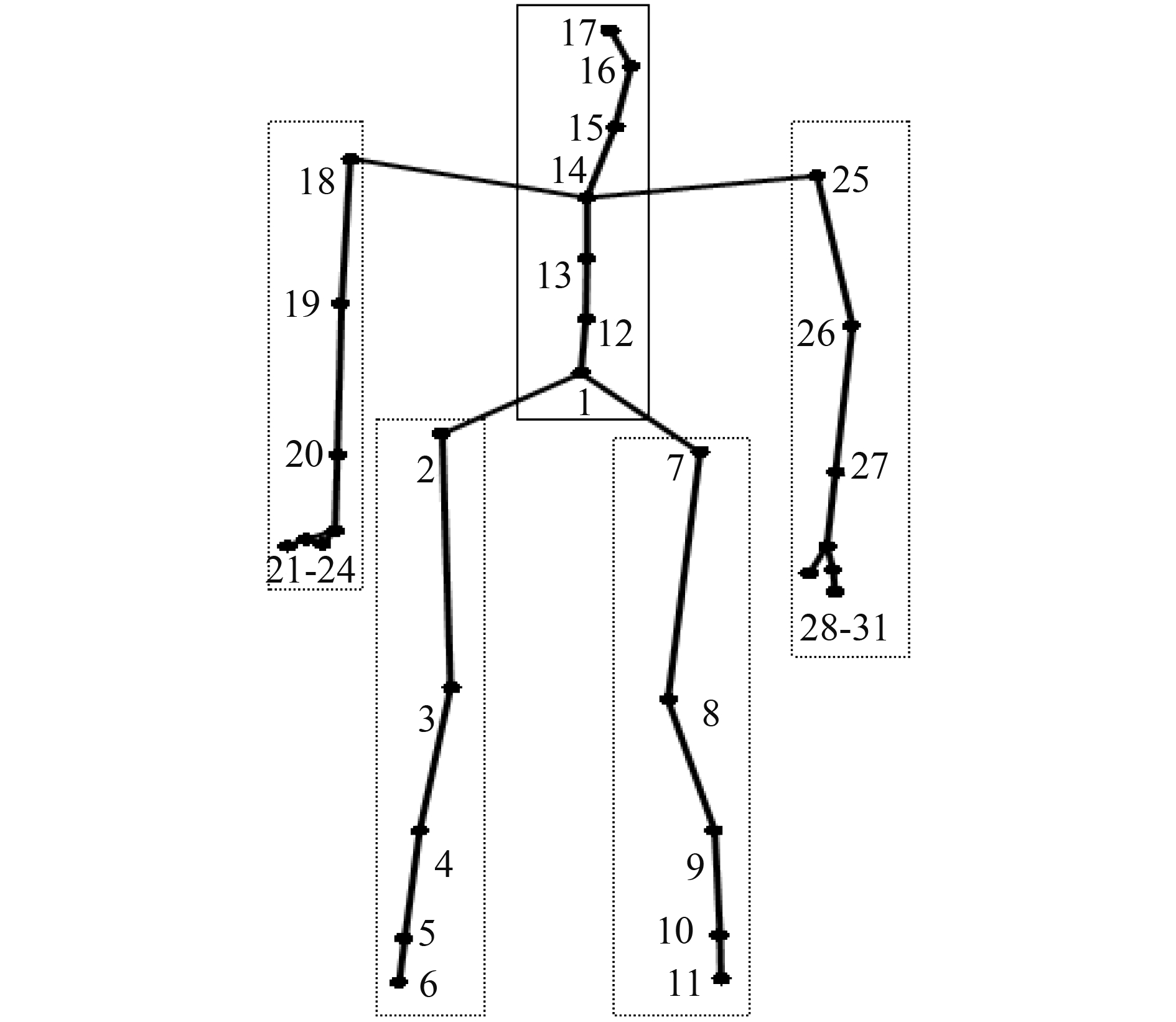
如图2所示, 将人体结构图划分为5个运动链接, 每个链都是一个关节点集合:
c1={1, 2, 3, 4, 5, 6}, c2={1, 7, 8, 9, 10, 11}, c3={1, 12, 13, 14, 15, 16, 17}, c4={14, 25, 26, 27, 28, 29, 30, 31}, c5={14, 18, 19, 20, 21, 22, 23, 24}, 集合中的数字对应图2和图1(b)中的标记点.
|
图 2 人体组成部位分割图 |
初始化: Δy(k)=0, 其中k=1, 2,…, 31, 并令
循环计算:
对i=1→5
对j=2→ci集合的长度;
令k=ci, k–1=ci[j–1];
根据公式(1)计算得到
根据公式(2)计算得到Δy(k);
终止里层循环
终止外层循环
| ${y_c}^{(k)} = \Delta {y^{(k - 1)}} + \frac{{{y^{(k)}} - {y^{(k - 1)}}}}{{||{y^{(k)}} - {y^{(k - 1)}}|{|_2}}}{L_{k,k - 1}}$ | (1) |
| $\Delta {y^{(k)}} = {y_c}^{(k)} - {y^{(k)}}$ | (2) |
其中, y(k)表示第k个关节点的三维坐标, 是第k–1个关节点的子节点,
| ${{F}_i} = {{\rm{[}}{X_{i,1}},{Y_{i,1}},{Z_{i,1}},{X_{i,2}},{Y_{i,2}},{Z_{i,2}},...,{X_{i,d}},{Y_{i,d}},{Z_{i,d}}{\rm{]}}^{\rm{T}}}$ | (3) |
其中, d表示一共有d个点,
此时F表示的仍然是世界坐标系下的MOCAP数据, 为了变换为局部坐标, 定义初等变换矩阵E, 令F1=E×F, 表示整个运动序列中由同一根骨骼连接的标记点的坐标之差, 例如, 第i帧的点2分别与点1和点3在同一根骨骼上, 点d和点(d–1)在同一根骨骼上, 则
| $\begin{array}{l}{F}{{\bf{1}}_i} = {\rm{[}}{X_{i,1}},{Y_{i,1}},{Z_{i,1}},{X_{i,2}} - {X_{i,1}},{Y_{i,2}} - {Y_{i,1}},{Z_{i,2}} - {Z_{i,1}},\\\;\;\;\;\;\;\;\;\;\;\;{X_{i,3}} - {X_{i,2}},{Y_{i,3}} - {Y_{i,2}},{Z_{i,3}} - {Z_{i,2}},\cdots,\\\;\;\;\;\;\;\;\;\;\;\;{X_{i,d}} - {X_{i,d - 1}},{Y_{i,d}} - {Y_{i,d - 1}},{Z_{i,d}} - {Z_{i,d - 1}}{{\rm{]}}^{\rm{T}}}\end{array}$ | (4) |
变换后的坐标表示的是同一骨骼上相邻标记点的坐标差, 即为局部坐标, 反映了各标记点相对位置.
为了利用骨骼不变这个约束, 再进行如下处理:
| ${F}{\bf{2}} = sign({F}{\bf{1}})({F}{\bf{1}} * {F}{\bf{1}})$ | (5) |
*表示哈达码乘积, 该式将F1的每个元素平方, 同时保留符号信息来消除平方带来的相对位置的模糊性. 对F1缺失部分的符号可以通过相邻帧对应点的符号得到, 对于缺失较长时间的序列可以先利用矩阵填充[6]理论来粗略地恢复数据, 从而得到符号信息. 根据骨骼长度不变这个条件, 可以得到F2中同一个点的三个坐标的绝对值之和始终为定值, 即:
| ${T}i \times {F}{{\bf{2}}_i} = {T}i \times {F}{{\bf{2}}_j} = {L}\;\;\;\;\;i,j \le N$ | (6) |
其中, L表示骨骼长度矩阵,
经过以上处理得到的F2为坐标标准化后的数据, 可以体现运动数据的本质特征, 使相似运动数据的差异性变小. 同时这个处理过程在保留F1的符号信息的情况下是可逆的:
| ${F} = {{E}^{ - 1}}{\rm{\{ }}{\mathop{\rm sign}\nolimits} ({F}{\bf{1}}) * {\mathop{\rm sqrt}\nolimits} {\rm{[}}{\mathop{\rm sign}\nolimits} ({F}{\bf{1}}) * {F}{\bf{2}}){\rm{]\} }}$ | (7) |
其中, sqrt()表示对矩阵每个元素求平方根.
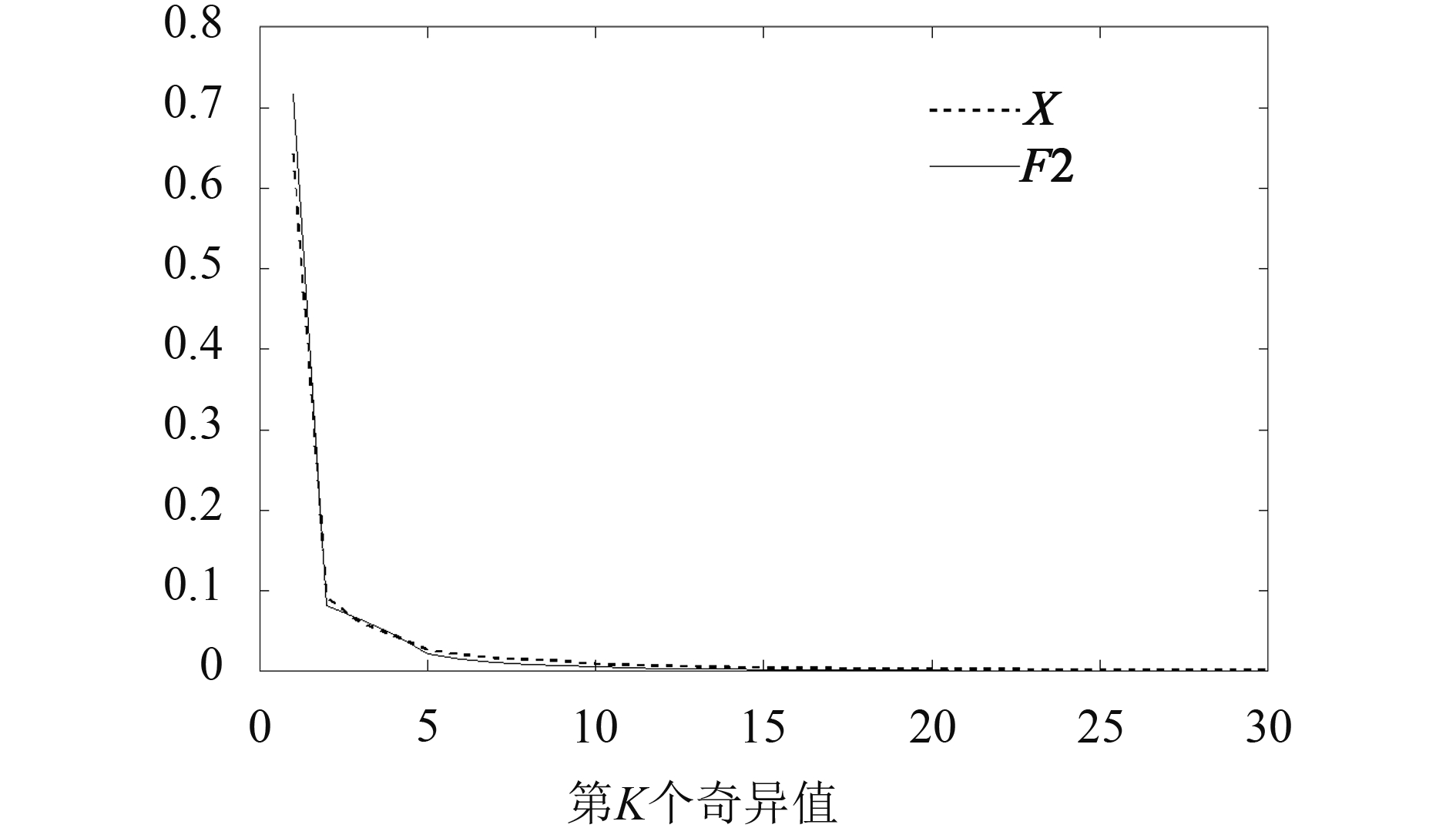
为了表明上述处理过程没有破坏运动序列的相关性, 对原始序列X和变换后的序列F2别进行奇异值分解, 将奇异值从大到小排列, 并进行归一化处理[6](每个奇异值除以所有奇异值的和), 于是得到X和F2的标准化奇异值图谱.
通过图3发现F2的曲线和X的曲线趋于0的速度相当, 甚至先趋于0, 说明F2的秩更低, 其数据相关性相比原始数据并没有减少甚至更高.
|
图 3 序列49_02的标准化奇异值 |
1.2 分割组合
按图2所示的划分将MOCAP数据分成5个部分来分别处理[13–15]. 因为人体进行不同种类运动时, 人体的某个部位的运动往往是相似的, 所以按人体不同部位划分后分别处理可以更好地体现MOCAP数据的局部特征. 如表1所示, 用相对坐标差代替世界坐标来表示各部分组成标记点. 表1中的数字相减表示对应点的各坐标值相减. 经过变换后的坐标点表示的就是相邻标记点的相对位置, 整个MOCAP数据表示的是相邻标记点的相对位置变化.
| 表 1 各部位组成点 |
由于本文针对的是同一帧中相邻标记点连续缺失的情况, 这样的分割处理可能会导致处理后的某一部分的标记点缺失很多, 甚至可能全部缺失, 所以再将这5部分每相连的3部分组合, 充分利用各个部位运动时存在的相关性. 组合方式如表2所示.
| 表 2 各部位组合表 |
分割组合后每个部分表示如下:
| ${F}{{\bf{3}}^i} = {\rm{[}}{F}{\bf{3}}_1^i,{F}{\bf{3}}_2^i,\cdots,{F}{\bf{3}}_N^i{\rm{]}},i = 1,2,\cdots,5$ | (8) |
如果对MOCAP进行逐帧独立处理, 将会忽略了帧与帧之间的相关性, 所以用滑动窗处理数据, 将连续几帧的数据合为一列[13–15]. 这样就充分发掘了相邻帧之间的相关性.
对于式(8)中的
| ${F}{\bf{3}}(M)_j^i = {\rm{[}}{F}{{\bf{3}}_{(j - 1) \times M + 1}},\cdots,{F}{{\bf{3}}_{j \times M}}{\rm{]}}$ | (9) |
将这M帧合为一列, 记为
| $\begin{array}{l}{{Y}^i} = {\rm{[}}{Y}_i^i,{Y}_2^i,\cdots,{Y}_S^i{\rm{]}},\;{{\rm{R}}^{{d_i} \times M}} \to {{\rm{R}}^{({d^i}) \times 1}}\\i = 1,2,\cdots,5,\;\;{d^i} = {d_i} \times M\;\;\end{array}$ | (10) |
用稀疏表示来恢复缺失数据的模型如下, 设X为某一信号的真实数据, A为其退化算子. 用下式表示观测到的数据:
| ${X}{\bf{1}} = {AX}$ | (11) |
设冗余字典D为关于X的一个字典, 通过稀疏编码求解下式:
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{W}} \;\;\;||{W}|{|_0}\\& {\rm s.t.}\;{X} = {DW}\end{aligned}\right.$ | (12) |
可以得到一个足够稀疏的向量W0, 使得X=DW0. W0满足
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{w}} \;\;\;||{W}|{|_0}\\& {\rm s.t.}\;{X}{\bf{1}} = {ADW}\end{aligned}\right.$ | (13) |
可以得到观测数据X1关于退化后的字典AD也存在一个稀疏表示向量W1, 使得X1=ADW1. 假设W1是足够稀疏的, 也就是满足
为了减小重构误差, 要进行字典训练得到合适的字典. 用来进行训练的是进行预处理后的数据. 字典训练的目标函数是最小化观测部分和缺失部分的稀疏表示的差异, 也就是要最小化重构误差. 但是和Feng等提出的SMBS[15]算法不同, 本文不仅最小化缺失部分的重构误差, 还考虑到观测部分的轻微噪声, 为了训练出能精确地重构观测部分的字典, 将观测部分的重构误差也考虑进来, 所以本文字典训练的目标函数是最小化整个运动序列的重构误差.
在理想字典D下, 通过求解下式, 可以得到稀疏表示系数.
| $\mathop {\min }\limits_{{{{W}}^i}} ||{{A}^i}{{Y}^i} - {{A}^i}{{D}^i}{{W}^i}||_{\;{\rm F}}^2 + \lambda _1||{{W}^i}|{|_{\;\;1}}$ | (14) |
其中Yi为预处理后的数据,
根据整个序列的重构误差定义损失函数为:
| ${{\mathop{ L}\nolimits} ^i}({Y}^i,{D}^i,{W}^i) = \sum\limits_{j = 1}^N {\frac{1}{2}||{Y}_j^i - {{D}^i}{W}_j^i||_{\mathop{\rm F}\nolimits} ^2} $ | (15) |
根据式(6)和(14)构造骨骼长度约束:
| ${{{B}}^i}{{L}} = {{{B}}^i}{{T}}{{{D}}^i}{{{W}}^i}\;$ | (16) |
其中, Bi是与退化算子Ai对应的骨骼提取算子, 作用是提取骨骼矩阵中的缺失部分. 式(16)左边的L表示的是已知的骨骼矩阵, 右边TDiWi表示的是恢复后的骨骼矩阵,
在损失函数式(15)中加入骨骼长度约束项, 来最小化骨骼长度恢复误差:
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{W}} \frac{1}{2}||{{{A}}^i}{{{Y}}^i} - {{{A}}^i}{{{D}}^i}{{{W}}^i}||_{\;{\mathop{\rm F}\nolimits} }^2 + {\lambda _1}||{{{W}}^i}|{|_{\;1}}\\& \;\;\;\;\;\;\;\;\; + \frac{{{\lambda _2}}}{2}||{{{B}}^i}{{L}} - {{{B}}^i}{{{T}}^i}{{{D}}^i}{{{W}}^i}||_{\;{\mathop{\rm F}\nolimits} }^2\\& {\rm{s}}{\rm{.t}}{\rm{.}}\;{{{D}}^i} = {\rm{[}}{{D}}_1^i,...,{{D}}_K^i{\rm{]}},\;||{{D}}_m^i|{|_{\;2}} \le 1,1 \le m \le {K^i}\end{aligned}\right.$ | (17) |
定义Pi, Qi:
| ${{{P}}^i} = \left( {\begin{array}{*{20}{c}}{{{{A}}^i}{{{Y}}^i}}\\{\sqrt {{\lambda _2}} {{{B}}^i}{{L}}}\end{array}} \right),\;\;{{{Q}}^i} = \left( {\begin{array}{*{20}{c}}{{{{A}}^i}}\\{\sqrt {{\lambda _2}} {{{B}}^i}{{{T}}^i}}\end{array}} \right){{{D}}^i}$ | (18) |
则字典训练的目标函数如下式:
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{D}} {{{L}}^i}{\rm{(}}{{Y}}_{}^i,{{D}}_{}^i,{{W}}_{}^i{\rm{)}}\\& {\rm{s}}{\rm{.t}}.\;{\rm{arg}}\mathop {\min }\limits_{{{{W}}_i}} \frac{1}{2}||{{{P}}^i} - {{{Q}}^i}{{{W}}^i}||_{\mathop{\rm F}\nolimits} ^2 + {\lambda _1}||{{{W}}^i}|{|_1}\\& ||{{D}}_m^i|{|_2} \le 1,1 \le m \le {K^i}\end{aligned}\right.$ | (19) |
对于式(19)可以交替求解Wi和Di.
固定稀疏Wi, 式(19)变为:
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{{{D}}^i}} \frac{1}{2}||{{P}}_{}^i - {{{Q}}^i}{{W}}_{}^i||_{\rm{F}}^{\rm{2}}\\& {\rm s.t.}\;{{{D}}^i} = {\rm{[}}{{D}}_1^i,\cdots,{{D}}_K^i{\rm{]}},||{{D}}_m^i|{|_2} \le 1\end{aligned}\right.$ | (20) |
用拉格朗日对偶[19]求解式(20), 得到字典Di.
固定字典Di, 式(19)变为:
| $\mathop {\min }\limits_{{{{W}}^i}} \frac{1}{2}||{{{P}}^i} - {{{Q}}^i}{{{W}}^i}||_{\;{\rm F}}^2 + {\lambda _1}||{{{W}}^i}|{|_{{\rm{1}}}}$ | (21) |
式(21)是一个L1范数最小化问题, 可以用增广拉格朗日对偶法[20]求解, 也可以用近端梯度下降法[21]求解.
交替求解式(20)和式(21)可以得到能有效用于重构数据的字典.
整个字典的训练过程和K-SVD[22]算法类似, 只是在求解稀疏表示系数时有所不同.
3 数据恢复 3.1 目标函数当得到字典后, 对测试样本进行稀疏求解. 为了方便表示求解过程, 同时不失一般性, 对变量进行简写, 通过下式表示的目标函对数据逐列求解稀疏表示系数.
| $\left\{\begin{aligned}& \mathop {\min }\limits_{{W}} \;\;\;\;||{{W}}|{|_{1}}\\& {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{{AY}} = {{ADW}},\;\;{{BL}} = {{BTDW}}\end{aligned}\right.$ | (22) |
其中, Y表示预处理后的测试样本某一帧的数据, A、W, 分别表示相应的退化算子和待求系数, AY表示已知的观测数据, B为骨骼提取算子, BL表示缺失部分的骨骼长度矩阵.
3.2 目标函数求解在观测部分有轻微噪声时, 骨骼约束项反过来会影响系数W来更好地对观测部分数据去噪. 令Y1=AY, 将式(22)写为:
| $\left\{\begin{aligned}&\mathop {\min }\limits_{{W}} \frac{1}{2}||{Y}{\bf{1}} - {ADW}||_{\;{\rm{F}}}^2 + \lambda _1||{W}||{_{0}}\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{BL} = {BTDW}\end{aligned}\right.$ | (23) |
再将式(23)写成无约束的拉格朗日形式, 同时用L1范数近似非凸的L0范数:
| $\begin{array}{l}\mathop {\min }\limits_{{W}} \frac{1}{2}||{Y}{\bf{1}} - {ADW}||_{{\rm{ F}}}^2 + \lambda 1||{W}||{_1} + \frac{{{\lambda _2}}}{2}||{BL} - {BTDW}||_{\;{\rm{F}}}^{\rm{2}}\end{array}$ | (24) |
式(24)是一个LASSO问题的变形, 用近端梯度下降法[21]求解.
| $\mathop {\min }\limits_{{W}} \;\;\;\;{\mathop{ g}\nolimits} {\rm{(}}{{W}}{\rm{)}} + {\mathop{ h}\nolimits} {\rm{(}}{{W}}{\rm{)}}$ | (25) |
其中,
| $\begin{array}{l}{\mathop{ g}\nolimits} {\rm{(}}{W}{\rm{)}} = \frac{1}{2}||{Y}{\bf{1}} - {DW}||_{\mathop{\rm F}\nolimits} ^2\; + \frac{{{\lambda _2}}}{2}||{BL} - {BTDW}||_{\mathop{\rm F}\nolimits} ^2\end{array}$ | (26) |
| ${\mathop{ h}\nolimits} {\rm{(}}{{W}}{\rm{)}} = \lambda _1||{{W}}|{|_{\;1}}$ | (27) |
g(W)是凸的, 可微的, h(W)是闭凸的.
对于任意的凸函数f(W), 定义proximal map算子如下:
| ${{\mathop{ prox}\nolimits} _{t,{\mathop{ f}\nolimits} {\rm{(}}{{W}}{\rm{)}}}} = \mathop {\arg \min {\rm{(}}{\mathop{ f}\nolimits} {\rm{(}}{{U}}{\rm{)}}}\limits_{{U}} + \frac{1}{{2t}}||{{U}} - {{W}}||_{\;{\rm{F}}}^2{\rm{)}}$ | (28) |
其中, t为步长. 根据近端梯度算法[21]可知, Wk的迭代公式如下:
| ${{{W}}^k} = {{\mathop{prox}\nolimits} _{{t^k},{\mathop{ h}\nolimits} {\rm{(}}{{W}}{\rm{)}}}}{\rm{(}}{{{W}}^{k - 1}} - {t^k}\nabla {{g(}}{{{W}}^{k - 1}}{\rm{))}}$ | (29) |
其中,
| $\begin{array}{l}\nabla {\mathop{ g}\nolimits} {\rm{(}}{{W}}{\rm{)}} = - {{\rm{(}}{{AD}})^{\rm{T}}}{\rm{(}}{{Y1}} - {{ADW}}{\rm{)}} \\[6pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-\lambda _2{{\rm{(}}{{BTD}})^{\rm{T}}}{\rm{(}}{{BL}} - {{BTDW}}{\rm{)}}\end{array}$ | (30) |
将式(29)带入式(28)得:
| $\begin{array}{l}{{{W}}^k} = \mathop {{\rm{arg}}\min }\limits_{{U}} \;{\rm{(}}\;{\mathop{ h}\nolimits} ({{U}}{\rm{)}}\;\; + \frac{1}{{2{t^k}}}||{{U}} - {{{W}}^{k - 1}} + {t^k}\nabla {{g(}}{{{W}}^{k - 1}}{\rm{)}}||_{\;{\rm{F}}}^2)\\[6pt]\;\;\;\;\;\; \;= \mathop {{\rm{arg min}}}\limits_{{U}} \;{\rm{(}}\;{\lambda _1}||{{U}}|{|_{\;1}} + \frac{1}{{2{t^k}}}||{{U}} - {{{W}}^{k - 1}}\; + {t^k}\nabla {\mathop{ g}\nolimits} {\rm{(}}{{{W}}^{k - 1}}{\rm{)}}||_{\;{\rm{F}}\;}^2)\end{array}$ | (31) |
式(31)利用软阈值算法可得:
| $\begin{array}{l}{{{W}}^k} = {\mathop{\rm sign}\nolimits} {\rm{(}}{{{W}}^{k - 1}} - {t^k}\nabla {\mathop{ g}\nolimits} {\rm{(}}{{{W}}^{k - 1}}{\rm{))}} \\[6pt]\;\;\;\;\;\;\;\;\;\;*\max {\rm{(}}|{{{W}}^{k - 1}} - {t^k}\nabla {\mathop{ g}\nolimits} {\rm{(}}{{{W}}^{k - 1}}{\rm{)}}| - 2{t^k}\lambda _1,0{\rm{)}}\end{array}$ | (32) |
步长t的更新如下式所示:
| $\left\{\begin{aligned}&t{h^k} = \frac{1}{2}\frac{{|\Delta {{W}}|}}{{|\Delta {{{W}}^{\rm{T}}}{\rm{(}}\nabla {\rm{g}}({{{W}}^k}{\rm{)}} - \nabla {\mathop{\rm g}\nolimits} {\rm{(}}{{{W}}^{k - 1}}{\rm{))}}|}}\\& \Delta W = \frac{1}{2}{\rm{(}}{{{W}}^k} - {{{W}}^{k - 1}}{\rm{)}}\\& {t^k} = \min {\rm{(}}\alpha {t^{k - 1}},\max (\beta {t^{k - 1}},t{h^k}{\rm{))}}\end{aligned}\right.$ | (33) |
其中α和β为给定常数. 所以交替求解式(31)和式(33)得到W, 再由W求得Yr.
求得Yr后, 通过求重叠部分的平均值消除延迟窗的作用, 通过式(7)逆变换求得预处理前的数据, 然后组合各部分获得完整的数据, 再通过骨骼标准化算法最终可以得到原始的数据Xr.
4 实验 4.1 实验设计由于字典训练对的训练集数量要求比较大, 而本实验室的所采集的数据有限(MOCAP数据采集比较耗时), 无法单独使用这些数据作为训练集, 所以实验从CMU数据库中选取3种不同的运动: run, boxing, basketball, 在每一类运动中随机选取两个序列做测试集, 其余的作为训练集. 这三种运动分别对应跑步, 拳击和篮球, 是比较有代表性的三种运动. 其中跑步代表了运动过程中具有一定周期性的的运动, 而其它两种代表不具周期性的运动. 而且在进行这三种运动时, 身体每个部位的运动都比较剧烈, 在采集数据时各个位置的标记点也容易发生缺失.
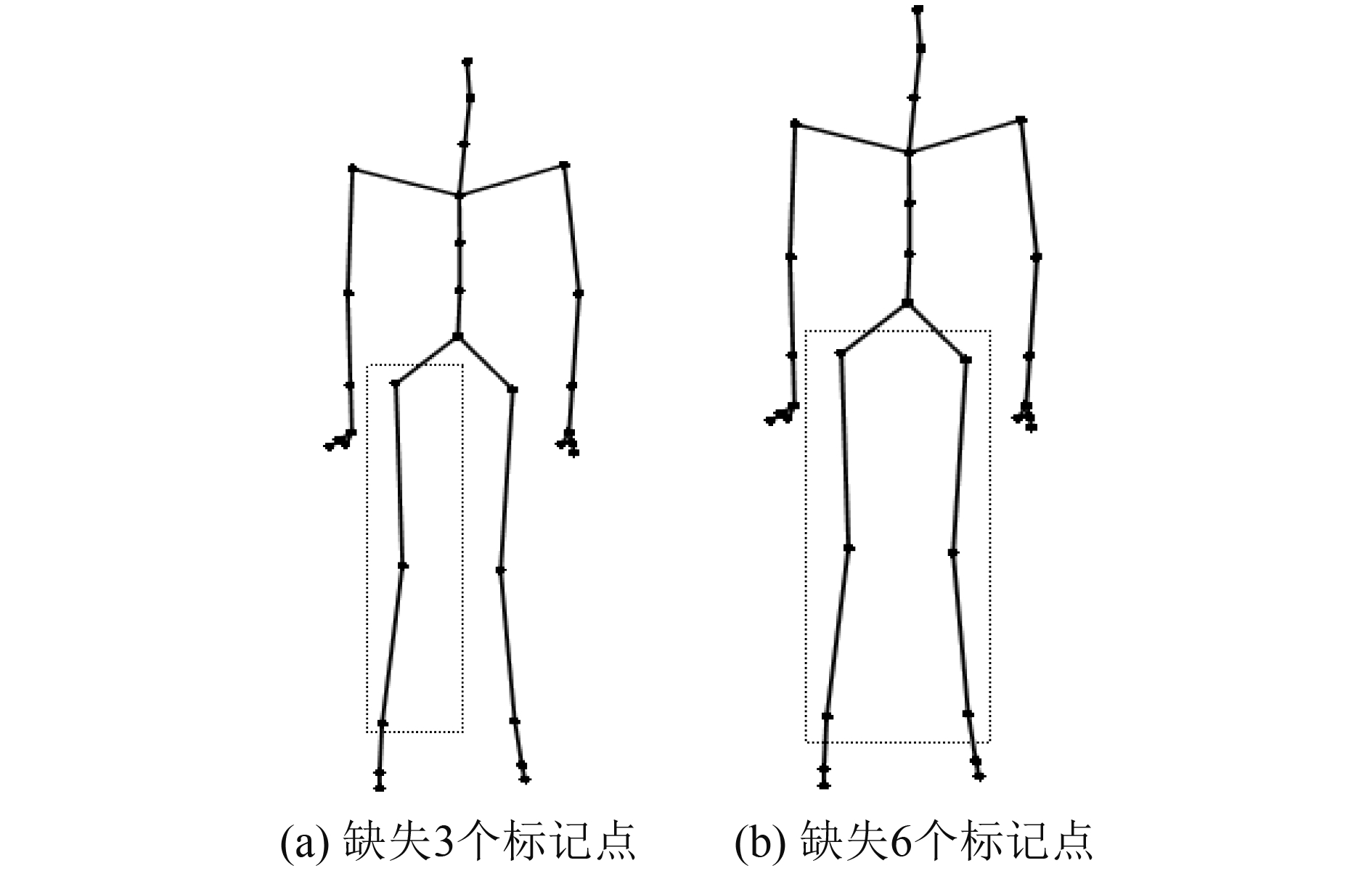
当对测试集进行预处理时, 由于标记点有缺失, 同一骨骼上的标记点坐标相减时, 会导致缺失点变多——如果点2分别与点1和点3在同一根骨骼上, 那么当点2缺失时, 点2与点3, 点2与点1的坐标之差都无法计算, 即视为缺失. 如果原数据缺失的标记点成随机分布, 那么预处理后的数据的缺失会大大增加, 极端情况会导致缺失数据翻倍. 如图4所示(方框选中的部分表示缺失), 本文针对的是实际采集数据过程中经常出现的同一帧中相邻标记点在空间域和时间域连续缺失的问题, 而对这样的缺失数据进行预处理, 不会导致处理后的数据增加过多额外的缺失.
本实验利用实验室的设备采集了与这三种运动相类似的运动数据. 当同一帧中相邻标记点连续缺失时, 参考采集数据中缺失数据的缺失分布, 对所选训练集和测试集构造一系列退化算子, 使得测试集的缺失更加符合实际情况. 最终构造的退化算子分为两类, 每类都使测试样本连续缺失40%帧, 第一类使缺失帧缺失连续缺失3个标记点, 第二类使缺失帧连续缺失6个标记点. 最后, 为了验证本算法对轻微噪声的鲁棒性, 直接对预处理后的测试样本添加信噪比为60的高斯噪声.
|
图 4 缺失标记点位置示意图 |
实验中主要有6个参数. 在进行字典训练时λ1从集合{10–2, 10–3, 10–4, 10–5, 10–6}中选取进行调节, 最终定为10–4; λ2从集合{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7}中选取调节, 定为0.4; 原子个数K设为1000, M设为6. 对测试集进行失真恢复时, λ1同样设为10–4, λ2也是从集合{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7}中选取调节, 若根据每一帧的缺失不同分别选取不同的λ2会提高恢复精确度, 但考虑到计算效率并综合整个序列的恢复精度, λ2也设为0.4.
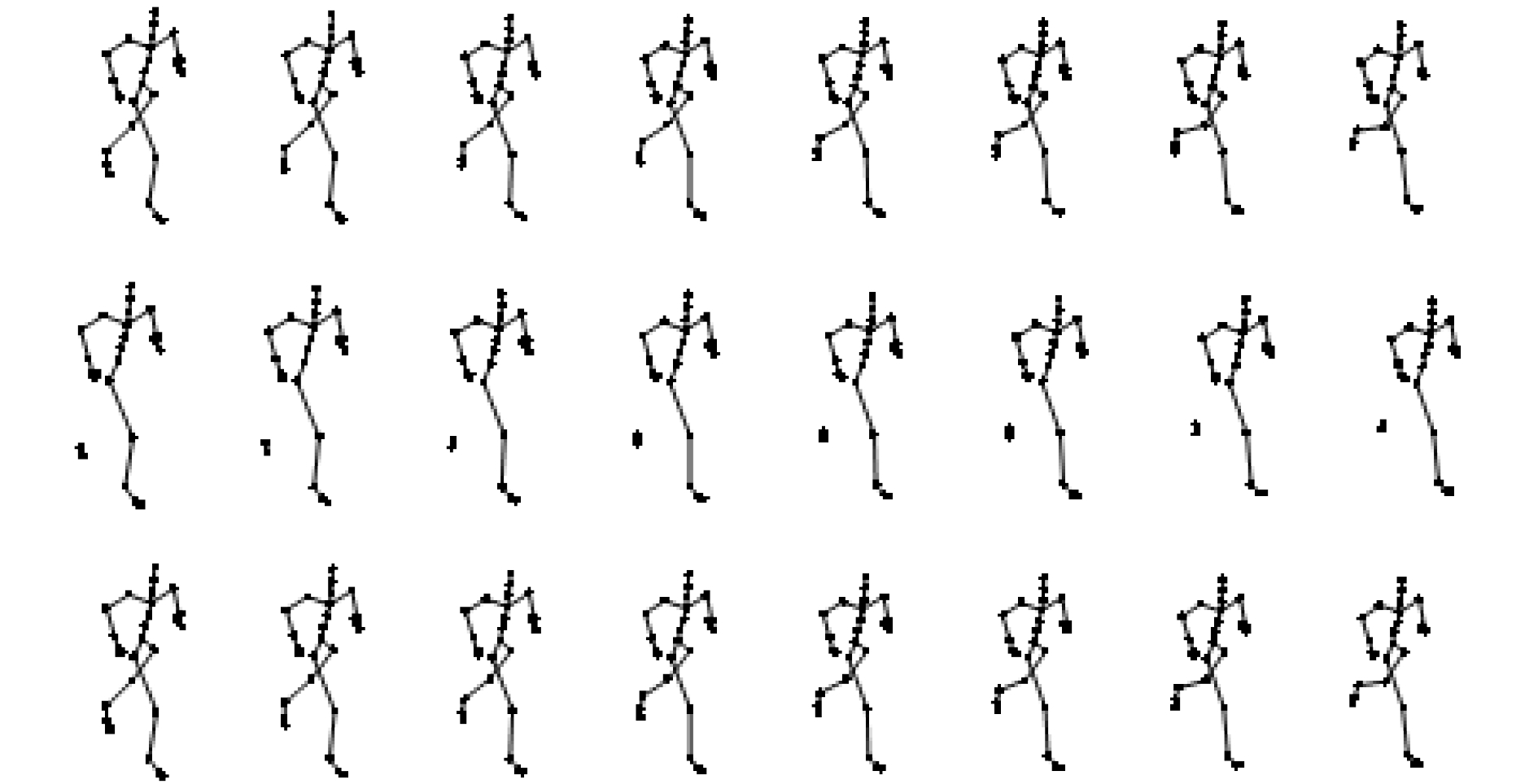
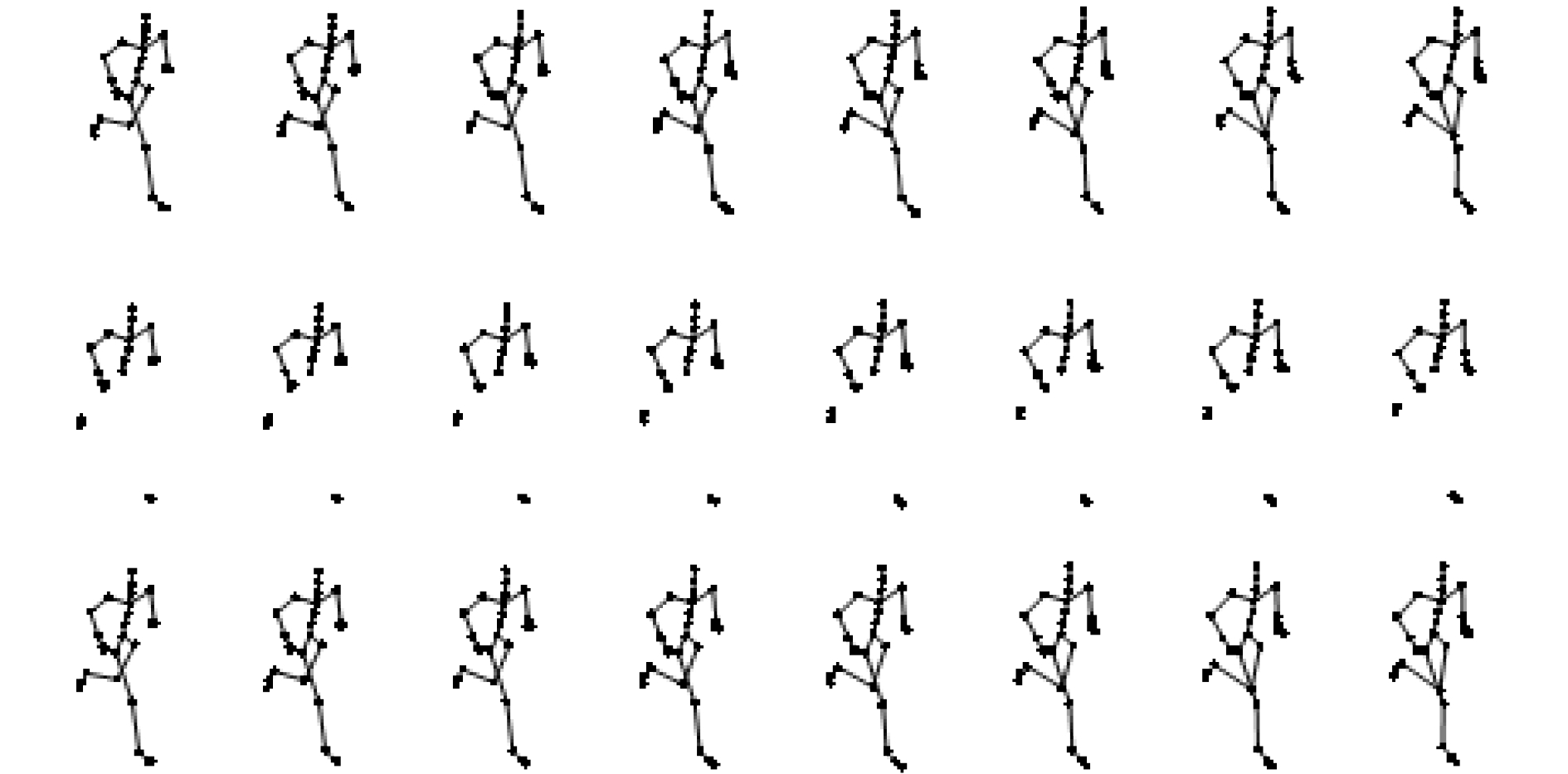
4.2 实验仿真结果图5和图6分别表示序列09_01(run)每一帧缺失3个标记点和6个标记点时的恢复情况, 从上到下分别为真实的序列, 缺失的序列和用本文算法恢复的序列.
|
图 5 缺失3个标记点的运动恢复序列比较图 |
从图5和图6可知, 恢复的运动序列在视觉上几乎和真实的运动序列一样.
用均方根误差(Root Mean Squared Error, RMSE)从数值上来衡量恢复误差.
|
图 6 缺失6个标记点的运动恢复序列比较图 |
X为真实数据, Xr为实验恢复的数据, np为缺失的数据的总个数.
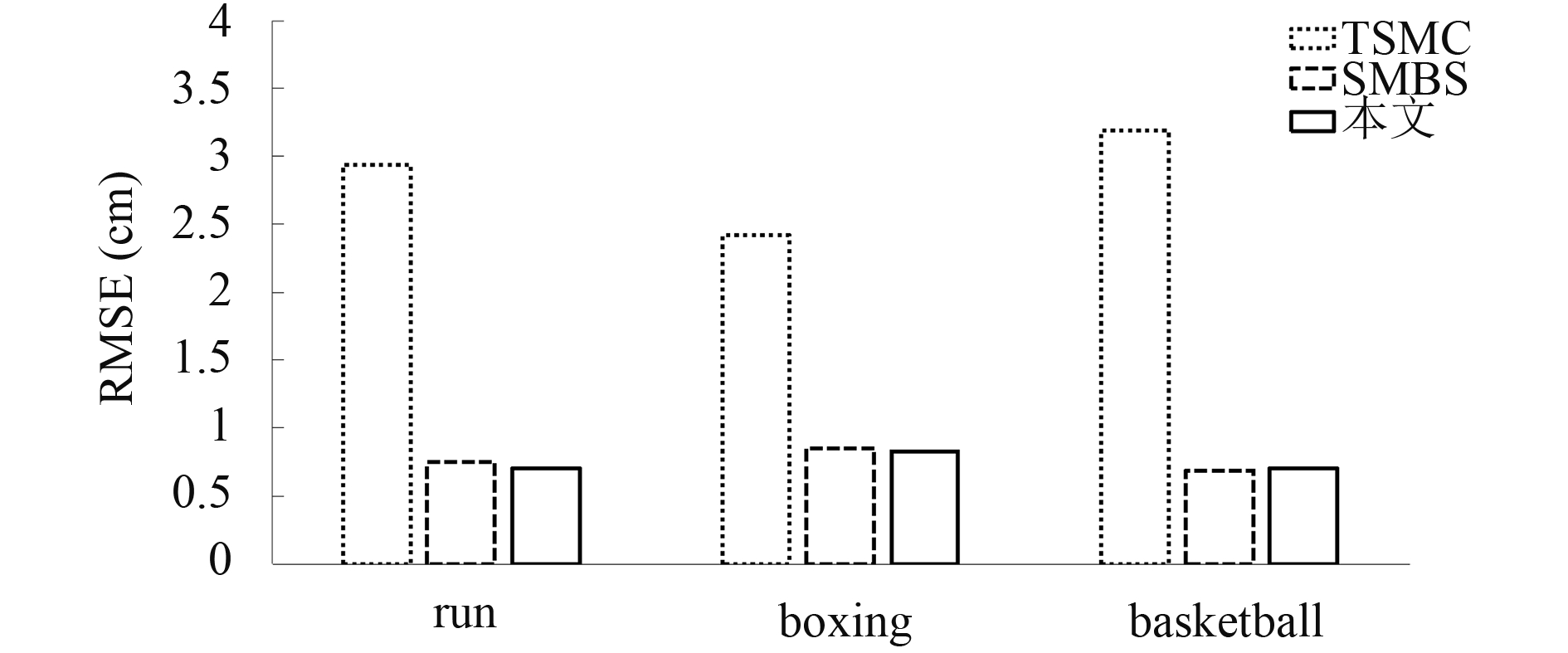
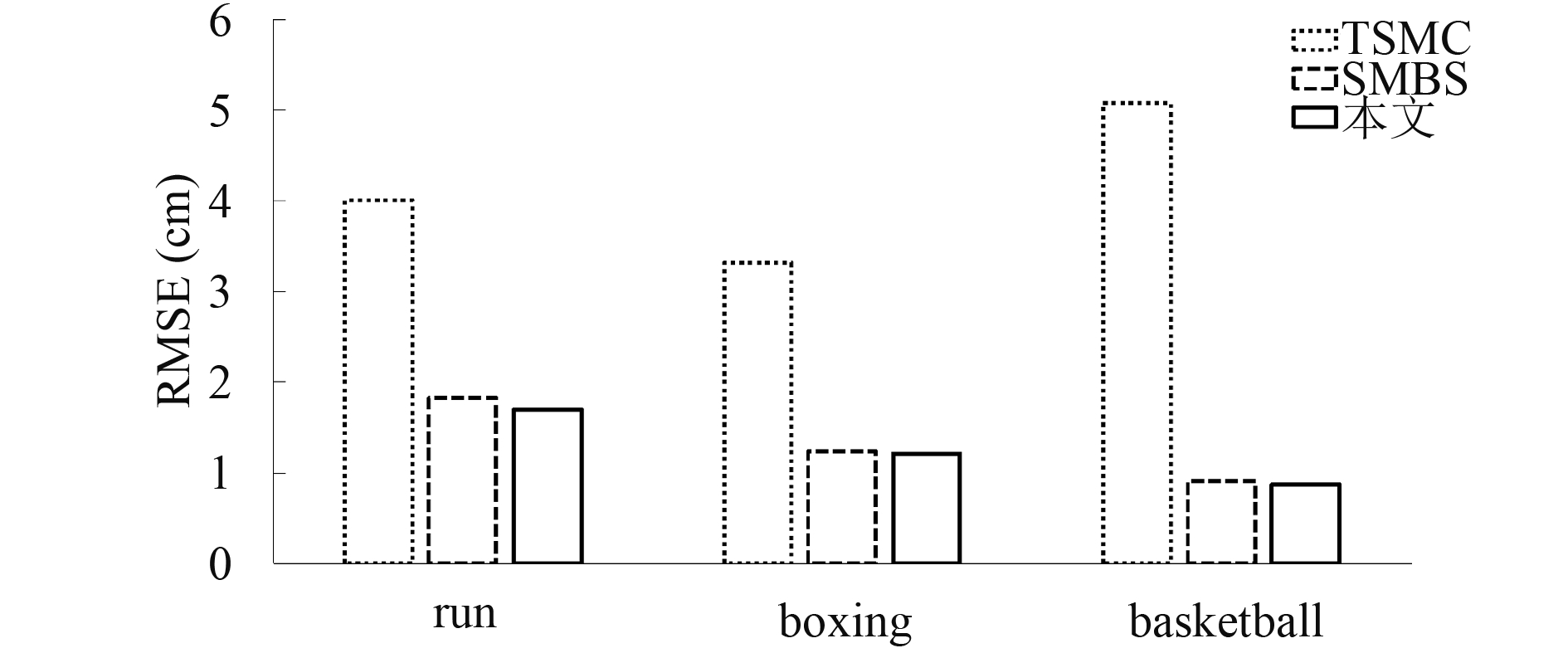
图7和图8分别表示在缺失标记点数目为3和6(包括各种不同缺失位置的情形), 连续缺失帧数为整个序列帧数40%的情况下, 三种运动在TSMC[10]算法, SMBS[15]算法和本文算法恢复下的平均坐标恢复误差.
|
图 7 每帧缺失3个标记点时不同算法的误差 |
|
图 8 每帧缺失6个标记点时不同算法的误差 |
本实验还比较了不同算法的坐标恢复误差随着缺失率增加的变化情况, 图9为序列06_02(basketball)在缺失标记点数为6时的误差变化图.
由图9可知, TSMC算法对缺失率变化很敏感, 随着缺失率的增加, 坐标恢复误差会明显增加; 而SMBS算法和本文算法对不同的缺失率的恢复效果很稳定. 这是因为SMBS算法和本文算法都利用了同一帧标记点之间的相关性, 而TSMC算法主要是利用数据的统计特性, 连续缺失率的增加会破坏数据的统计特性. 另一方面本文利用了骨骼约束, 会提高坐标恢复的稳定性.

|
图 9 不同算法的坐标恢复误差变化图 |
由图6到图9的实验结果可知, 本文算法在坐标恢复精度上明显好于TSMC算法, 当缺失率小于0.4时, 本文算法和SMBS算法恢复效果相当, 但随着缺失率的增加, 本文算法将好于SMBS算法.
本实验还比较了在不同算法下恢复的骨骼长度误差. 用下式来表示骨骼长度误差:
| ${{\mathop{ RMSE}\nolimits} _{\rm skel}}({{L}},{{{L}}_r}) = \sqrt {\frac{1}{{{n_L}}}||{{L}} - {{T}}{{{L}}_r}||_{\rm{F}}^2} $ | (34) |
其中, nL为总的骨骼数, Lr为恢复数据的骨骼矩阵. 表3为每帧标记点缺失数为6时的比较结果(单位为cm).
| 表 3 各算法骨骼长度误差(单位: cm) |
通过表3可知本文算法恢复的骨骼长度误差远小于其它两种算法, 精确度达到10–4 cm.
综合上述实验结果可知, 本文提出的算法同时提高了坐标恢复精度和骨骼长度恢复精度.
5 结论与展望本文通过使用一种新的预处理数据的方法, 将运动序列进行骨骼标准化处理, 消除不同人体的骨骼长度差异的影响, 再将各标记点坐标从原始世界坐标系下的坐标转化为表示相邻标记点坐标差的局部坐标, 减小运动数据的差异性, 使不同运动序列的局部运动也具有相似性. 为了充分利用局部运动的相似性, 又将运动序列按人体部位进行分割组合处理. 在字典训练时, 通过重叠窗处理充分利用了帧与帧之间的相关性, 使恢复的运动序列更具连续性. 通过最小化重构误差来获得训练字典的目标函数, 同时加入骨骼约束项, 使训练的字典在重构运动序列时能保持骨骼长度的不变的特性. 在得到字典后, 通过近端梯度下降法来求得解系数, 从而获得重构的运动数据, 最后通过逆变换获得最终的运动序列. 实验结果表明文提出的算法, 在保持良好的恢复效果的同时, 保持了骨骼长度不变性, 这使得恢复的运动序列更加自然, 也便于数据后续的存储.
在接下来的工作里, 将研究如何利用深度学习来恢复失真的人体运动捕捉序列. 准备将MOCAP数据的特性和用于图像恢复的深度学习算法相结合, 提出基于深度学习的MOCAP数据失真恢复算法.
| [1] |
Bruderlin A, Williams L. Motion signal processing. Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA. 1995. 97–104.
|
| [2] |
Yamane K, Nakamura Y. Dynamics filter-concept and implementation of online motion generator for human figures. IEEE Transactions on Robotics and Automation, 2003, 19(3): 421-432. DOI:10.1109/TRA.2003.810579 |
| [3] |
Hsieh CC, Kuo PL. An impulsive noise reduction agent for rigid body motion data using B-spline wavelets. Expert Systems with Applications, 2008, 34(3): 1733-1741. DOI:10.1016/j.eswa.2007.01.030 |
| [4] |
Li L, McCann J, Pollard N, et al. BoLeRO: A principled technique for including bone length constraints in motion capture occlusion filling. Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Madrid, Spain. 2010. 179–188.
|
| [5] |
Li L, McCann J, Pollard NS, et al. DynaMMo: Mining and summarization of coevolving sequences with missing values. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France. 2009. 507–516.
|
| [6] |
Lai RYQ, Yuen PC, Lee KKW. Motion capture data completion and denoising by singular value thresholding. Proc Eurographics Association, 2011, 11(3): 924-929. |
| [7] |
Tan CH, Hou JH, Chau LP. Human motion capture data recovery using trajectory-based matrix completion. Electronics Letters, 2013, 49(12): 752-754. DOI:10.1049/el.2013.0442 |
| [8] |
彭淑娟, 赫高峰, 柳欣, 等. 基于运动分割和稀疏低秩分解的失真人体运动捕捉数据恢复. 计算机辅助设计与图形学学报, 2015, 27(4): 721-730, 737. |
| [9] |
赫高峰, 彭淑娟, 柳欣, 等. 结合模糊聚类和投影近似点算法的缺失人体运动捕捉数据重构. 计算机辅助设计与图形学学报, 2015, 27(8): 1416-1425. |
| [10] |
Feng YF, Xiao J, Zhuang YT, et al. Exploiting temporal stability and low-rank structure for motion capture data refinement. Information Sciences, 2014(277): 777-793. DOI:10.1016/j.ins.2014.03.013 |
| [11] |
Hou JH, Chau LP, He Y, et al. Human motion capture data recovery via trajectory-based sparse representation. Proceedings of the 20th IEEE International Conference on Image Processing. Melbourne, VIC, Australia. 2014. 709–713.
|
| [12] |
Xiao J, Feng YF, Hu WY. Predicting missing markers in human motion capture using l1-sparse representation. Computer Animation & Virtual Worlds, 2011, 22(2-3): 221-228. |
| [13] |
Xiao J, Feng YF, Ji MM, et al. Sparse motion bases selection for human motion denoising. Signal Processing, 2015(110): 108-122. DOI:10.1016/j.sigpro.2014.08.017 |
| [14] |
Feng YF, Ji MM, Xiao J, et al. Mining spatial-temporal patterns and structural sparsity for human motion data denoising. IEEE Transactions on Cybernetics, 2015, 45(12): 2693-2706. DOI:10.1109/TCYB.2014.2381659 |
| [15] |
Wang Z, Feng YF, Liu S, et al. A 3D human motion refinement method based on sparse motion bases selection. Proceedings of the 29th International Conference on Computer Animation and Social Agents. Geneva, Switzerland. 2016. 53–60.
|
| [16] |
Tan CH, Hou JH, Chau LP. Motion capture data recovery using skeleton constrained singular value thresholding. The Visual Computer, 2015, 31(11): 1521-1532. DOI:10.1007/s00371-014-1031-5 |
| [17] |
Lai RYQ, Yuen PC, Lee KW, et al. Interactive character posing by sparse coding. arXiv:1201.1409, 2012.
|
| [18] |
Elad M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing. New York, USA: Springer, 2010: 44–46.
|
| [19] |
Lee H, Battle A, Raina R, et al. Efficient sparse coding algorithms. Proceedings of the 19th International Conference on Neural Information Processing Systems. Cambridge, MA, USA. 2006. 801–808.
|
| [20] |
Yang AY, Sastry SS, Ganesh A, et al. Fast ℓ1-minimization algorithms and an application in robust face recognition: A review. Proceedings of the 17th IEEE International Conference on Image Processing. Hong Kong, China. 2010. 1849–1852.
|
| [21] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [22] |
Aharon M, Elad M, Bruckstein A. rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation
. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
 2018, Vol. 27
2018, Vol. 27


