随着移动网络技术的高速发展, 网络新闻生产、传播速度都呈爆炸性的增长, 人们逐渐从新闻信息匮乏的时代进入了新闻信息过载的时代. 无论是新闻消费者还是新闻生产者都遇到了很大的挑战: 从消费者角度来看, 如何从大量新闻中发现自己感兴趣的新闻是一件非常困难的事情; 从生产者角度来看, 如何提高新闻浏览量和受众规模, 也是一件很困难的事情. 与此同时, 随着社会节奏的加快, 新闻消费者倾向于在更加碎片化的时间内浏览新闻, 因此新闻消费者主动搜索新闻以解决信息过载问题的意愿也就更低, 换言之, 用户希望在花费更少时间的前提下得到更适合自己的新闻.

个性化推荐系统^[1]就是解决这一问题的重要工具. 在新闻推荐领域, 个性化新闻推荐系统通过联系用户和新闻, 一方面帮助用户发现对自己有价值的新闻, 另一方面让新闻能够展现在对它感兴趣的用户面前, 从而实现新闻消费者和新闻生产者的双赢. 其中协同过滤算法^[2]是推荐系统中应用较为广泛的推荐算法, 该算法基于邻域; 根据领域选取的区别, 可以分为基于用户的协同过滤算法^[3]以及基于物品的协同过滤算法^[4]. 而在新闻推荐算法领域, 一般更适合使用基于用户的协同过滤推荐算法, 因为在一个新闻系统中, 用户量是相对固定且变化不明显的, 维护基于用户的协同过滤算法在性能上有更好的表现.

但基于用户的协同过滤算法容易忽视新闻信息的特性, 导致推荐新闻的时效性不足, 降低了新闻推荐的实际接受率; 并且需要不断调整相似用户的新闻信息表, 在数据量大时, 算法时间开销会非常大.

本文针对上述问题, 提出了基于新闻时效性的协同过滤推荐算法, 该方法充分考虑到了新闻信息老化^[5]的特点, 通过建立新闻的时效性模型, 改进了基于用户的协同过滤系统中对最近邻用户的选择; 在维护用户相似度的矩阵时, 将新闻集进行提前过滤, 保留时效性较高的新闻信息. 在新闻信息量较大的情况下也能维持算法的高性能, 本文利用该改进的算法, 对某网络新闻系统的新闻、用户行为数据集进行了仿真实验, 证明了本文所提方法的有效性.

1 新闻时效性模型和基于用户的协同过滤推荐算法 1.1 新闻时效性模型

对于推荐系统而言, 不同类型的物品具有不同的生命周期, 即它们的时效性会有很大的差别. 例如新闻信息就要比电影的生命周期短很多; 用户可能会满意对很久之前电影的推荐, 因为电影的信息熵并不会因为时间的推移而减少; 而对用户推荐老旧新闻, 很多时候都是无效的, 因为新闻的时效性非常重要; 即使是比较重要的历史性新闻信息, 实质上也算是过期信息, 对用户浏览新闻并无帮助.

从新闻信息的产生, 推荐, 成为热点, 衰退到最后的消失, 新闻信息在时间轴上总是呈现一定的规律; 这一点和应用信息计量学中的文献老化理论是相似的, 例如文献^[6,7]就通过文献老化模型来描述网络信息的效用变化. 因此我们可以根据信息老化的特点, 建立新闻推荐系统的时效性模型, 定义如下:

定义1. 新闻发布时刻 ${t_n}$ . 新闻发布时刻是指当新闻被生产完毕并正式发布的时间节点, 但还没被个性化推荐系统加入相似新闻集. 一般而言, 这个时刻与推荐系统更新时刻越近则说明新闻越新, 在经过初级过滤系统时, 它被过滤的可能性越低.

定义2. 推荐算法更新时刻 ${t_a}$ . 由于新闻会不断发布, 因此推荐算法更新新闻信息库的时间也要根据系统的计算能力与实际新闻发布数量来设定, 一般而言, 两次更新间隔越短, 推荐效果越好, 但会消耗很大的系统性能, 需要根据实际系统来设定这个参数.

定义3. 新闻生命周期 ${T_s}$ . 生命周期是指在新闻发布后, 自某个时刻起不再有新闻消费者对其做出消费行为, 从这个时刻( ${t_n} + {T_s}$ )起, 零星的阅读行为可以认为是系统噪声不予考虑.

根据文献信息老化规律模型, 即贝尔纳在1958年提出的信息老化的负指数模型:

$C\left( t \right){\rm{ = }}k{e^{ - at}}$

(1)

公式(1)中, $t$ 为文献的出版年龄, $C\left( t \right)$ 表示 $t$ 年时文献被引用频率. $k$ 是一个与文献分类有关的常数, $a$ 为文献的老化率.

将此模型应用于新闻信息, 可以用公式(2)定义, 将在后面验证负指数模型对新闻老化规律模型的适用性.

$S\left( {{t_n},t} \right){\rm{ = }}{e^{ - a\left( {t - {t_n}} \right) + b}}$

(2)

其中, $t$ 表示当前时刻, ${t_n}$ 为新闻发布时刻, ${{S}}\left( {{t_n},{t_{}}} \right)$ 表示新闻在t时刻时的用户反馈统计数量, 需要根据新闻系统设定合适的时间粒度, 来统计该时刻分段的用户反馈数量. $a$ 是该新闻的老化系数, 表示该新闻随着时间推移其效果的衰减系数, $a$ 越小, 说明这条新闻的时效性越强; $b$ 则为某一个常数, 和新闻在发布后的初始统计时间粒度内的用户反馈统计数量有关, 以第一个统计时间段 $t = {t_n}$ 为例, 在第一个时间粒度内, 用户反馈统计数量 $S\left( {{t_n},t} \right) = {e^b}$ , $b$ 参数受新闻初始阅读量影响较大, 但不会表现新闻时效性的变化趋势; 即 $b$ 较大的新闻会拥有比较大的初始阅读量, 但不能保证衰减速度慢; 在本文研究的时效性改进算法中, 更关心新闻本身的时效性变化趋势, 所以进行线性回归分析, 计算出 $a$ 、 $b$ 后, 主要采取 $a$ 作为推荐算法的输入, 实际上对公式(2)变形后, 可以在公式(3)中更清楚的认识到老化参数与时间推移之间的关系:

$S\left( {{t_n},t} \right){\rm{ = }}{e^b}{e^{ - a\left( {t - {t_n}} \right) }}$

(3)

变形后, 对老化曲线拟合更贴近于常见的负指数模型, 在数学表达上也更加直观. 只要求出老化系数 $a$ 即可.

对于一条特定的新闻而言, 老化系数 $a$ 代表了其在发布后传播效果的衰减速度, 发布后衰减不明显的新闻是时效性较强的新闻, 新闻消费者认为其有很高的时效价值; 而当一条新闻到达自己的生命周期 ${T_s}$ 后, 那么此新闻就没有时效价值了.

1.2 基于用户的协同过滤算法原理

基于用户的协同过滤算法(以下简称UserCF算法)是推荐系统中最常见的算法之一, 应用十分广泛; 主要包括两个步骤, 首先寻找与目标用户兴趣度相似的用户集合. 然后找出在这个用户集合中的用户喜欢而目标用户尚未关注的物品信息, 将其推荐给目标用户.

在计算两个用户的兴趣相似度时, 主要利用行为的相似度来计算兴趣的相似度. 给定用户 $u$ 和用户 $v$ , 集合 $N\left( u \right)$ 表示用户 $u$ 曾经有过正反馈的物品集合, 集合 $N\left( v \right)$ 为用户 $v$ 曾经有过正反馈的物品集合, 就可以计算 $u$ 和 $v$ 的兴趣相似度 $w_v^u$ ,常见的相似度计算公式有两种, 第一种是杰卡德相似度计算公式^[8]:

$w_v^u{\rm{ = }}\frac{{\left| {N\left( u \right) \cap N\left( v \right)} \right|}}{{\left| {N\left( u \right) \cup N\left( v \right)} \right|}}$

第二种是余弦相似度计算公式:

$w_v^u{\rm{ = }}\frac{{\left| {N\left( u \right) \cap N\left( v \right)} \right|}}{{\sqrt {N\left( u \right)||N\left( v \right)} }}$

根据用户之间的兴趣相似度, 可以给用户推荐和他兴趣最相似的 $K$ 个用户喜欢的新闻, 公式(6)度量了UserCF算法中用户 $u$ 对新闻 $n$ 的感兴趣程度.

$p\left( {u,n} \right) = \mathop \sum \limits_{v \in S\left( {u,K} \right) \cap U\left( n \right)} {w_{uv}}{r_{vn}}$

(4)

在此式中, $S\left( {u,K} \right)$ 包含了与用户 $u$ 兴趣最为接近的 $K$ 个用户, $U\left( n \right)$ 是对新闻n有过行为的用户集合, ${w_{uv}}$ 是用户 $u$ 和用户 $v$ 的兴趣相似度, ${r_{vn}}$ 代表用户 $v$ 对新闻 $n$ 的交互评分, 由其阅读时长、新闻长度、点赞、评论等正反馈行为归一化得出, 以衡量用户对新闻的兴趣度. 计算出 $p\left( {u,n} \right)$ 后, 比较通用的做法是根据某个用户 $u$ 对新闻 $n$ 的预测评分 $p\left( {u,n} \right)$ , 做Top-N推荐, 即推荐出前 $N$ 个高评分结果.

2 基于新闻时效性的协同过滤算法 2.1 算法设计

传统的UserCF算法中没有考虑信息时效性的问题, 这种做法可能适合电影、电商类系统, 但却忽略了新闻信息的时效性. 为了解决这个问题, 本文结合上文中的新闻时效性模型, 根据新闻衰老系数与生命周期, 对推荐新闻预测评分进行加权, 同时过滤过时新闻, 降低了算法输入数据的规模, 从而提高了推荐的效果.

2.2 数据模型

(1) 新闻信息集合, 表示新闻系统中的新闻集合, 会根据生产者的输出而更新, 加入新的新闻. 用集合 $N = \left\{ {{n_1},{n_{2},} \cdots ,{n_i}} \right\}$ 来表示 $i$ 条新闻的集合, 这个集合用来计算用户相似度.

(2) 推荐系统输入新闻集合, 表示新上架的新闻, 作为推荐系统在选取推荐新闻时的输入集; 同时也用来计算新闻时效性. 用集合 ${\rm{}}M = \left\{ {{m_i}|{t_a} < {t_{{n_{{m_i}}}}} + {T_{{s_{{m_i}}}}}} \right\}$ 来表示. $M$ 集合包含了那些在推荐算法更新输入时刻仍然较为活跃, 并未消耗完生命周期的新闻, 这些新闻仍然有不少用户在阅读; 由于UserCF算法要进行比较复杂的用户偏好度计算, 同时要进行时效性模型的检验, 所以将输入集限定在仍然在生命周期内的新闻, 可以大幅降低算法复杂度.

(3) 用户信息集合, 表示新闻系统中的用户集合, 会根据系统用户的增加而更新, 但变化很缓慢. 用集合 $U = \left\{ {{u_1},{u_{2},} \cdots ,{u_k}} \right\}$ 来表示 $k$ 个用户的集合.

(4) 用户, 新闻兴趣矩阵 ${R_{i*u}}$ , 用户会对新闻做出不同的行为, 如阅读、点赞、分享及评论等; 通过用户行为偏好向量空间模型来计算用户对新闻兴趣值 ${r_{un}}$ .

(5) 新闻访问表, 用于记录新闻被阅读、收藏、赞操作及其具体时间, 用于计算新闻被访问随时间变化的趋势, 即其时效性.

2.3 通过时效性参数改进推荐算法

算法详细步骤如下:

1) 在推荐算法更新时刻 ${t_a}$ , 确定 $M$ 集合, 并对 $M$ 集合中的元素进行统计, 根据系统设定的时间粒度, 从新闻访问行为表中计算在每个时段内新闻被访问的数据. 通过时效性模型曲线拟合计算新闻老化率 $a$ , 并计算 $M$ 集合中新闻老化率 $a$ 的最大值, 记为 ${a_{\max}}$ .

2) 用户相似兴趣度计算, 可以选择余弦相似度计算, 也可以选择杰卡德相似度计算. 在选定相似度公式后, 计算用户相似兴趣度的输入集包含整个新闻集合 $N$ 与用户集合 $U$ , 而非新闻子集合 $M$ , 这是为了获取用户完整的历史兴趣爱好, 以构建正确的用户相似兴趣度矩阵. 在这里我们选取杰卡德相似度公式:

$w_v^u{\rm{ = }}\frac{{\left| {N\left( u \right) \cap N\left( v \right)} \right|}}{{\left| {N\left( u \right) \cup N\left( v \right)} \right|}}$

3) 基于时效性参数改良预测评分结果:

$p\left( {u,n} \right) = \mathop \sum \limits_{v \in S\left( {u,K} \right) \cap U\left( n \right)} {w_{uv}}{r_{vn}}\left( {1 - \frac{{{a_n}}}{{{a_{\max}}}}} \right)$

(5)

对 $M$ 集合中的新闻应用公式(8), 计算出用户对 $M$ 集合中新闻的兴趣度, 通过加入时效性参数作为加权, 即可得出最终预测兴趣评分.

4) 选取Top-N作为最后的推荐方法, 选择 $M$ 集合中最高兴趣评分的 $N$ 个元素作为用户推荐的结果.

3 实验分析

本文对某新闻报业集团的网络新闻数据与用户数据进行实验. 共计5436条新闻, 43 187个用户. 部分新闻数据如表1所示, 该表表示某个新闻的阅读情况.

3.1 时效性模型实验

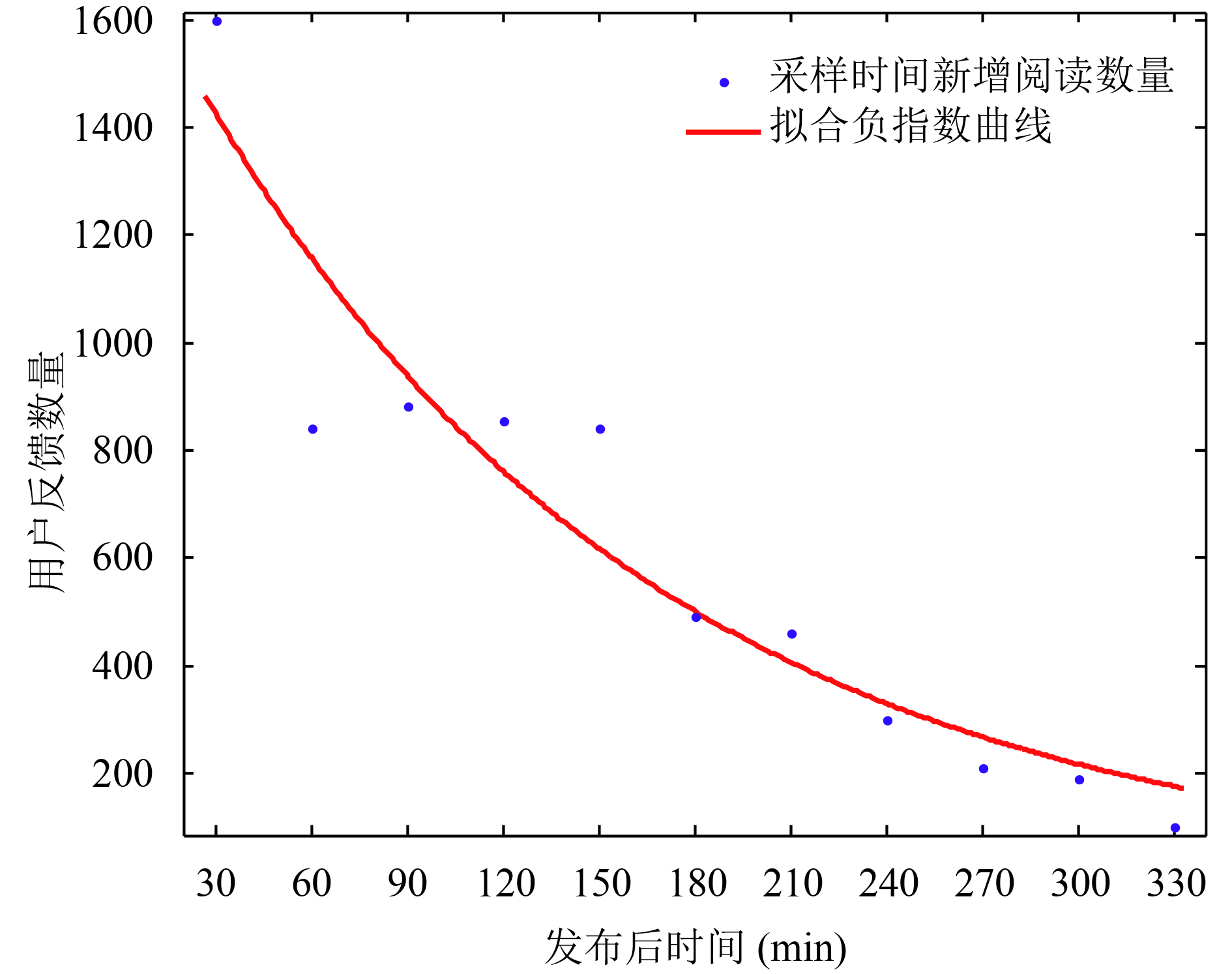
首先对新闻集进行时效性模型检验, 根据其阅读量变化, 使用负指数模型进行拟合校验, 以单条新闻为例, 图1即单条新闻阅读变化量拟合结果.

表2为其时效性模型检验结果. 对于本文的时效性模型而言, SSE与RMSE与模型输入数量级有关, 对结果没有太大的解释意义; R-square与Adjusted R-square则表达了拟合结果与目标模型的效果, 越接近1说明模型越好. 表2中对应新闻浏览量变化趋势比较符合时效性模型曲线, 即阅读量与时间之间有较强的相关关系, 可以根据其拟合得到的老化系数作为推荐模型的输入.

表3所示为对测试集合中的新闻进行时效性模型检验, 从中可以看出, 拟合结果R-square大于0.80的比例为70.7%, 即其与负指数时效性模型拟合度较好, 有较高的说服度, 这些新闻的主要特点是平均总阅读量比较高, 因此噪音表现不明显; 而剩余的新闻平均总阅读量比较低, 受关注度低, 即使在发布的第一时间, 也很少有用户关注; 对在发布后的某个特定时间段的抗噪音能力较差, 用户反馈统计数量容易受波动, 难以体现时效性变化的总体趋势.

针对时效性模型的拟合误差, 需要根据具体情况设定误差实验分析; 总体而言, 对于阅读量较大的新闻, 时效性模型是比较适用的, 拥有比较好的正确率与精度, 也可以从中看出新闻阅读量与时间的相关性; 对于抗噪声能力较差的非热门新闻, 可以将其剔除出新闻输入集合, 只对订阅用户推送, 因此就不会受到非精确时效衰减率影响.

3.2 基于时效性模型改进UserCF算法的实验

根据实验(1)的结果, 得出了时效性模型的新闻老化系数, 改进UserCF算法; 本实验采用Mahout^[9]作为UserCF框架, 在计算用户兴趣度时, 考虑时效性模型中老化系数的影响.

将实验(1)中的新闻数据集中R-square超过0.80的新闻集单独抽出, 形成一个新的新闻集A, 与原新闻集N分别作为新闻总集, 进行两次实验, 实验步骤相同, 输入不同, 其他参数一致. 最后与传统的UserCF算法作为对照比较.

本实验中, 将用户行为数据集随机且均匀分成8份, 6份作为训练集, 2份作为测试集, 通过准确率与召回率来评价推荐算法的效果:

式(9)为准确率的公式:

$Precision = \frac{{\mathop \sum \nolimits_u \left| {R\left( u \right) \cap T\left( u \right)} \right|}}{{\mathop \sum \nolimits_u \left| {R\left( u \right)} \right|}}$

(6)

式(10)为召回率的公式:

$Recall = \frac{{\mathop \sum \nolimits_u \left| {R\left( u \right) \cap T\left( u \right)} \right|}}{{\mathop \sum \nolimits_u \left| {T\left( u \right)} \right|}}$

(7)

其中 $R\left( u \right)$ 为推荐新闻集合, $T\left( u \right)$ 为用户实际喜欢的新闻信息. 准确率用于描述最终推荐列表中实际发生的用户-新闻兴趣评分, 召回率用于描述有多少比例的用户-新闻兴趣评分出现在最后的最终的推荐列表中.

表4为推荐算法实验结果, 首先对于不同的输入新闻集合N与A, A代表那些和时效性模型拟合程度较好的新闻数据集, 它们的平均阅读数量也较高, 抗噪声能力强; 实际上在一个推荐系统中, 热门新闻受推荐的概率会更大, 因此其准确率与召回率都会更高. 在传统的UserCF算法中, A集合有着更高的推荐准确率与召回率, 但与N集合差别并不大, UserCF算法没有考虑到时间推移的影响, 只响应了高阅读量新闻的特性, 略微提高了推荐准确率与召回率.

在相同的输入集合下, 改进后的UserCF算法有着更好的表现, 这是因为基于时效性模型改进的UserCF算法考虑到了新闻时效性衰减的因素, 较好地利用了老化系数, 降低了衰减较快新闻的权重; 对于和时效性模型拟合较好的新闻集合, 改进后的UserCF性能还会有提高, 这是因为这类新闻不仅衰减速度慢, 时效性强, 同时自身阅读量高, 故而推荐效果还会有所增强.

3.3 时效性模型误差分析

在时效性模型实验实验中, 针对拟合误差较大的新闻集合, 即R-square值低于0.80以下的新闻集合B, 进行误差分析与算法性能分析.

表5为误差新闻集实验结果. 对于R-square值较低的新闻集合, 由于其和时效性模型偏差较大, 拟合所得的老化率 $a$ 不能完全反应新闻实际失效的速度, 在引入UserCF算法时并不会大幅提高UserCF性能; 但从实际结果来看, 时效性模型改进的UserCF算法仍然有15%的提高. 这是因为高误差新闻集合中的新闻阅读量较少, 这些新闻很容易在算法的第一步时因为生命周期消耗殆尽, 从而被提前过滤. 没有进入输入集合中; 但相对于总新闻集合中的推荐实验结果, 这些误差使得时效性模型改进的UserCF算法的提高较为有限.

4 结论与展望

随着网络新闻量的爆发式增长, 如何在信息过载的情境下为新闻消费者提供合理的新闻推荐集成为了重点问题. 本文结合文献信息老化模型, 应用于新闻信息上, 利用时效性模型中的老化参数改进了基于用户的协同过滤算法, 对新闻-用户数据集进行了分析和研究. 从实验结果上看, 这种改进型算法适用于抗噪能力强的热门新闻, 能提高新闻推荐算法的准确率和召回率.

但是本文提出的方法只考虑了协同过滤算法中兴趣评分处理与新闻时效性的问题, 并没有解决协同过滤算法中冷启动^[10]问题, 同时也没有考虑到系统初始状态下的用户稀疏性^[11]问题. 所以该算法在未来还有很大的改进空间.