行人再识别是指在无重叠视域多摄像机监控系统中, 匹配不同摄像机视域中的行人目标. 行人再识别在目前的视频监控应用中是一个非常重要的任务, 该技术在行人检索[1]、多摄像机行人跟踪[2]等视频监控领域都有着重要的应用. 但由于在不同摄像机视域中, 行人受视角、姿势变化、光照条件、背景变化、摄像头设置等因素的影响, 导致同一行人的图像外貌存在着很大的差异, 使得行人再识别问题遇到了很大的挑战. 为了应对这些挑战, 近年来的广大研究者提出了许多的解决方法. 在行人图片特征提取方法中, 其最主要的是设计对不同行人具有区分性和对视角、光照、背景的变化具有鲁棒性的描述特征. 许多已经存在的行人再识别算法试图通过建立一个特有的, 健壮的代表特征来描述在各种变化环境下的行人外观. 文献[3]利用行人区域的对称性和不对称性将人的前景划分成不同的区域, 每个区域通过提取局部累积特征来处理姿态、视角和光照的变化. 文献[4]也提出了类似的方法, 用一个自适应的身体外形结构表示行人图像, 包括头、胸、大腿和小腿, 然后提取每个部分的颜色特征. 文献[5]提出了对行人图像的同一水平位置的滑动窗口进行扫描, 取所有滑动窗口的直方图相同bin的最大值作为该水平组的直方图特征. 最近, 显著性信息也出现在行人再识别上的应用研究[6–9], 文献[9]采用4种方向显著性加权融合学习的方法来度量一对行人图像的相似度.
除了有代表性的特征外, 距离度量学习也是行人再识别的另一个研究方面. 文献[10]首次提出距离测度学习的问题, 根据样本的类别, 将具有相同类别标签的样本组成正样本对, 不同类别标签的样本构成负样本对, 然后利用这些样本对作为约束条件来训练得到一个马氏矩阵. 在文献[11]提出一种PRDC算法, 算法的原理是最优化相关距离的比较. 文献[12]提出了一种叫KISSME (Keep It Simple and Straightforward Metric)的度量学习算法, 该算法将样本之间的差向量看作是高斯分布中的一个点, 同类样本的差向量分布在同一个高斯分布中, 而不同样本之间的差向量分布在另一个高斯分布中, 然后用概率的比值来度量样本之间的距离. 文献[13]在文献[12]的基础上提出了核学习的思想, 把低维线性不可分的特征空间投影到高维可分的非线性空间中再进行KISSME度量学习. 这些算法通过学习一个马氏距离相似度函数(Mahalanobis Similarity Function, MSF)来度量一对行人图像的相似度. 然而, MSF只与特征差分空间有关, 忽略了每个个体的独立特征, 因此对于同一个人在不同摄像机中的很大表观变化的捕捉能力有限.
基于上述情况, 提出了一种基于双向关系相似度函数学习方法(Bidirectional Relationship Similarity Function, BRSF)来计算一对行人图像的相似度. 利用KISSME算法的思想进行相似度函数学习, 把一对样本特征的自相关关系和互相关关系用高斯分布来表示, 最终高斯分布的比值转换为BRSF的形式, 进而得到一个对背景、视角、姿势变化有着更好的鲁棒性的相似度函数.
1 双向关系相似度函数的学习 1.1 BRSF算法近年来, 行人再识别问题的研究者也尝试设计合适的相似度学习算法, 更好地计算一对行人图像的相似度. 当给定一对来源于非重叠摄像机视角的行人图像, 行人图像对(i, j)的特征向量分别为Xi和Xj, Xi, Xj∈Rd, d是特征维度. 这些算法通过学习一个马氏距离相似度函数fM (Xi, Xj)来度量一对行人图像的相似度. MSF形式如下式(1)所示:
| ${f_{\rm M}}\left( {{X_i},{X_j}} \right) = - {\left( {{X_i} - {X_j}} \right)^{\rm T}}{\rm M}\left( {{X_i} - {X_j}} \right)\;$ | (1) |
其中, M是一个半正定矩阵, 用于保证相似度函数的对称性.
正如引言所述, MSF只与特征差分空间有关, 忽略了每个个体的独立特征, 因此对于同一个人在不同摄像机中的很大的外观变化的捕捉能力有限. 本文通过学习一个双向关系相似度函数fB (Xi, Xj)来计算一对行人图像的相似度. BRSF是MSF的泛化形式, BRSF的形式如下式(2)所示:
| ${f_{\rm B}}\left( {{X_i},{X_j}} \right) = {X_i}^{\rm T}{\rm A}{X_i} + {X_j}^{\rm T}{\rm A}{X_j} + {X_i}^{\rm T}{\rm B}{X_j} + {X_j}^{\rm T}{\rm B}{X_i}$ | (2) |
其中A, B∈Rd×d. 因为一对行人图像的相似度有着对称性, 所以A和B不需要是半正定矩阵. 在BRSF中,
为了说明上述观点, 这里用一个一维空间的二分类例子来证明. 有两个类的样本分别服从[–10, –2]的均匀分布和[2, 10]的均匀分布. 当给定一个样本X=–3和另一个样本Y,图1显示了采用MSF和BRSF两种相似度函数, 样本X和样本Y的相似度的分布. 其中, S(X)=S(Y)表示X和Y属于同一个类, S(X)!=S(Y)表示X和Y属于不同的类. 当采用MSF, 即fM(X, Y)=–m(X–Y)2, 如图1(a)所示, 同类样本和不同类样本之间的相似度取值范围存在重叠的部分. MSF并不能完全分开上述两类样本, 在这里, m=1, 因为m并不改变两类样本之间相似度的相对关系. 当相似度函数采用BRSF, 相似度函数中的自相关矩阵和互相关矩阵不再互为负矩阵, 增强了自相关关系的影响, 即fB(X, Y)=–(X–Y)2+3XY, 如图1(b)所示, 上述两类样本被完全分开. 上述例子说明BRSF比MSF更具有区分性.
1.2 相似度度量函数的学习文献[12]中提出了一种KISSME的算法, 该方法没有使用到复杂的迭代优化的过程, 学习相似度度量函数的时间花销小. 因此把KISSME度量学习算法的思想应用到BRSF中. 一对行人图像(i, j)的特征向量为(Xi, Xj), Xi, Xj∈Rd, 则行人图像对(i, j)的相似度可以表示为式(3):
| $\delta \left( {{X_i},{X_j}} \right) = \log \left( {\frac{{p\left( {{X_i},{X_j}|{H_1}} \right)}}{{p\left( {{X_i},{X_j}|{H_0}} \right)}}} \right)$ | (3) |
其中, p(Xi, Xj|H1)表示一对行人图像对在假设H1是相关行人图像对的条件下(Xi, Xj)相似的概率. p(Xi, Xj| H0)表示一对行人图像对在假设H0是不相关行人图像对条件下(Xi, Xj)相似的概率. 如果δ(Xi, Xj)的值是比较大的, 则说明假设H1是成立的. 相反, δ(Xi, Xj)的值比较小, 则说明假设H1是不成立的, 则这对行人图像对是不相关行人图像对.
文献[12]假设行人图像对是高斯分布中的一个点, 则行人图像对的自相关关系和互相关关系分别用高斯分布来表示如下式(4)和式(5):
| ${{\delta _A}\left( {{X_i},{X_j}} \right) = }{\log \left( {\displaystyle\frac{{\displaystyle\frac{1}{{\sqrt {2\pi |\sum\nolimits_{A{y_{ij}} = 1} {} |} }}\exp \left[ { - \displaystyle\frac{1}{2}\left( {{X_i}^{ \rm T}\sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} {X_i} + {X_j}^{\rm T}\sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} {X_j}} \right)} \right]}}{{\displaystyle\frac{1}{{\sqrt {2\pi |\sum\nolimits_{A{y_{ij}} = 0} {} |} }}\exp \left[ { - \displaystyle\frac{1}{2}\left( {{X_i}^{\rm T}\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} {X_i} + {X_j}^{\rm T}\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} {X_j}} \right)} \right]}}} \right)}$ | (4) |
| ${{\delta _C}\left( {{X_i},{X_j}} \right) = }{\log \left( {\displaystyle\frac{{\displaystyle\frac{1}{{\sqrt {2\pi |\sum\nolimits_{C{y_{ij}} = 1} {} |} }}\exp \left[ { - \displaystyle\frac{1}{2}\left( {{X_i}^{\rm T} \sum\nolimits_{C{y_{ij}} = 1}^{ - 1} {} {X_j} + {X_j}^{\rm T}\sum\nolimits_{C{y_{ij}} = 1}^{ - 1} {} {X_i}} \right)} \right]}}{{\displaystyle\frac{1}{{\sqrt {2\pi |\sum\nolimits_{C{y_{ij}} = 0} {} |} }}\exp \left[ { - \displaystyle\frac{1}{2}\left( {{X_i}^{\rm T}\sum\nolimits_{C{y_{ij}} = 0}^{ - 1} {} {X_j} + {X_j}^{\rm T}\sum\nolimits_{C{y_{ij}} = 0}^{ - 1} {} {X_i}} \right)} \right]}}} \right)}$ | (5) |
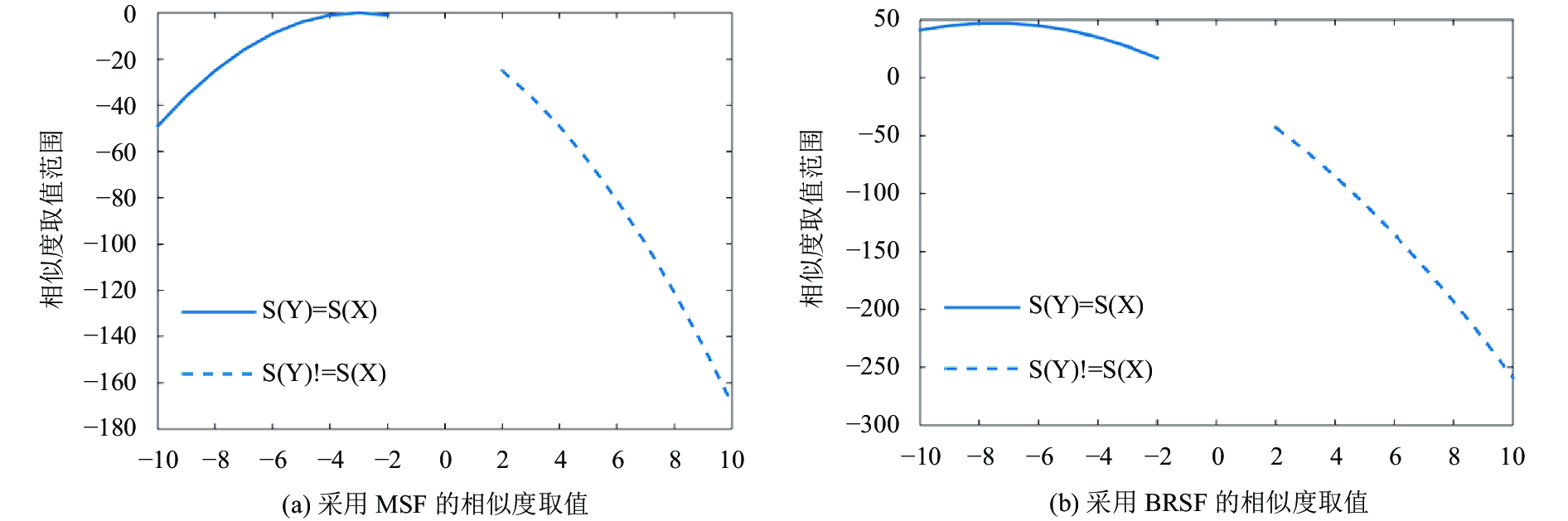
|
图 1 MSF与BRSF相似度取值的对比 |
其中, yij=1表示行人图像对(i, j)属于相关行人图像对. 反之, yij=0表示行人图像对(i, j)属于不相关行人图像对. 相关行人图像对的样本分布在同一个高斯分布中, 不相关行人图像对的样本分布在另一个高斯分布中. 在这里,
| $\sum\nolimits_{A{y_{ij}} = 1} {} = \sum\limits_{{y_{ij}} = 1} {{X_i}{X_i}^{\rm T} + {X_j}{X_j}^{\rm T}} $ | (6) |
| $\sum\nolimits_{A{y_{ij}} = 0} {} = \sum\limits_{{y_{ij}} = 0} {{X_i}{X_i}^{\rm T} + {X_j}{X_j}^{\rm T}} $ | (7) |
| $\sum\nolimits_{C{y_{ij}} = 1} {} = \sum\limits_{{y_{ij}} = 1} {{X_i}^{\rm T}{X_j} + {X_j}^{\rm T}{X_i}} $ | (8) |
| $\sum\nolimits_{C{y_{ij}} = 0} {} = \sum\limits_{{y_{ij}} = 0} {{X_i}^{\rm T}{X_j} + {X_j}^{\rm T}{X_i}} $ | (9) |
把式(4)的右边进行log简化, 我们重写式(4)得到式(10).
| $\begin{aligned}{\delta _A}\left( {{X_i},{X_j}} \right) = & {X_i}^{\rm T}\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} {X_i} + {X_j}^{\rm T}\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} {X_j}\\[4pt] & + \log \left( {|\sum\nolimits_{A{y_{ij}} = 0} {} |} \right)- {X_i}^{\rm T}\sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} {X_i} \\[4pt] & - {X_j}^{\rm T}\sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} {X_j}- \log \left( {|\sum\nolimits_{A{y_{ij}} = 1} {} |} \right)\end{aligned}$ | (10) |
在式(10)中常数项只是提供了一个补偿, 不影响最后的结果, 我们可以把式中常数项去掉, 将式(10)简化得到式(11):
| $\begin{aligned}{\delta _A}\left( {{X_i},{X_j}} \right) = & {X_i}^{\rm T}\left( {\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} - \sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} } \right){X_i}\\[4pt] &+{X_j}^{\rm T}\left( {\sum\nolimits_{A{y_{ij}} = 0}^{ - 1} {} - \sum\nolimits_{A{y_{ij}} = 1}^{ - 1} {} } \right){X_j}\end{aligned}$ | (11) |
同理, 式(5)也可以简化重写得到式(12):
| $\begin{aligned}{\delta _C}\left( {{X_i},{X_j}} \right) = & {X_i}^{\rm T}\left( {\sum\nolimits_{C{y_{ij}} = 0}^{ - 1} {} - \sum\nolimits_{C{y_{ij}} = 1}^{ - 1} {} } \right){X_i} \\[4pt] &+{X_j}^{\rm T}\left( {\sum\nolimits_{C{y_{ij}} = 0}^{ - 1} {} - \sum\nolimits_{C{y_{ij}} = 1}^{ - 1} {} } \right){X_j}\end{aligned}$ | (12) |
最后, 我们通过把式(11)和式(12)合并得到式(13), 式(13)就是我们的BRSF的形式.
| $\delta \left( {{X_i},{X_j}} \right) = {X_i}^{\rm T}{ A}{X_i} + {X_j}^{\rm T}{ A}{X_j} + {X_i}^{\rm T}{ B}{X_j} + {X_j}^{\rm T}{ B}{X_i}$ | (13) |
在这里, 我们得到了:
| ${ A} = \sum\nolimits_{{ A}{y_{ij}} = 0}^{ - 1} {\rm{ }} - {\rm{ }}\sum\nolimits_{{ A}{y_{ij}} = 1}^{ - 1} {\rm{ }} ,{ B} = \sum\nolimits_{C{y_{ij}} = 0}^{ - 1} {\rm{ }} - {\rm{ }}\sum\nolimits_{C{y_{ij}} = 1}^{ - 1} {\rm{ }} $ |
基于BRSF学习的行人再识别系统包括3个步骤: (1) 行人图像特征的提取; (2) BRSF学习; (3) 查询目标行人图像. 整个系统流程如图2所示, 其中BRSF是利用数据集离线学习得到.
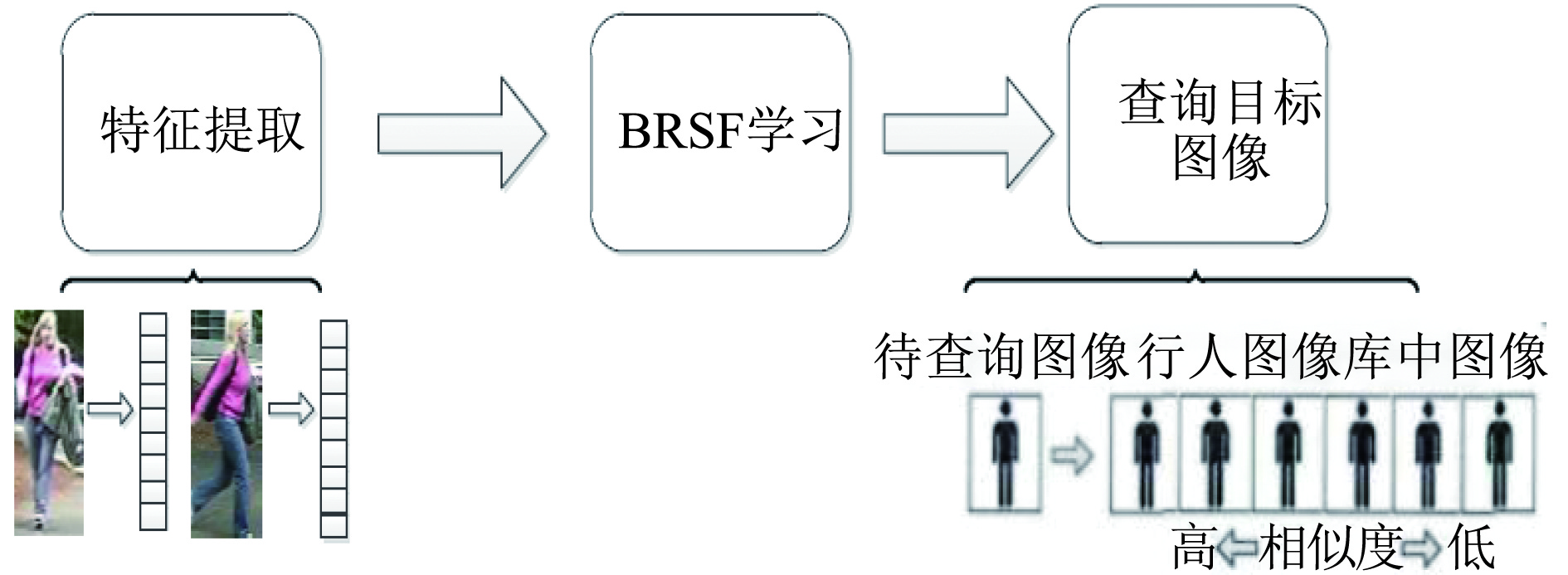
|
图 2 基于BRSF学习的行人再识别系统框架 |
2.1 行人图像特征的提取
颜色和纹理是描述行人图像非常重要的两个特征. 本文采用HSV、YCbCr和Lab三种颜色空间的颜色直方图和SILTP[14] (Scale Invariant Local Ternary Pattern)纹理直方图来描述一张行人图像. 不同的颜色空间采用不同的衡量标准, 所以对同一张行人图像描述的侧重点也各不相同. SILTP是著名的LBP (Local Binary Pattern)纹理描述算子的改进算法, LBP算法的缺点是对图像噪声比较敏感, 所以SILTP算法还结合了LTP (Local Ternary Patterns)算法取得了对图像噪声和光照变化具有更强的鲁棒性. 我们把一张行人图像归一化为128×48像素, 使用大小为10×10像素的滑动子窗口去描述行人图像的局部细节. 滑动子窗口的滑动方向是水平方向的, 每次滑动的步长为5个像素. 在每个子窗口中, 提取HSV、YCbCr和Lab三种颜色空间中每个通道的颜色直方图和SILTP纹理直方图. 为了解决不同摄像机下行人图像视角变化的问题, 在同一个水平位置上, 扫描所有子窗口, 取所有直方图相同bin的最大值作为该水平组的直方图特征. 这样得到的直方图特征不但对行人图像视角变化具有很好的鲁棒性, 而且可以捕捉到行人图像的局部细节特征. 图3显示滑动子窗口提取特征的过程.
在提取特征的过程, 我们考虑到了行人图像的多尺度信息. 在原始图像128×48像素的基础上进行两次金字塔降采样分别获得64×24像素的尺度和32×12的尺度图像. 在每个尺度的行人图像上重复上述的特征提取过程. 最后我们把所有特征级联形成行人图像的特性描述, 该特征的维数为9000维(3*3*16维颜色特征+34维SILTP特征)*(24+11+5水平组).
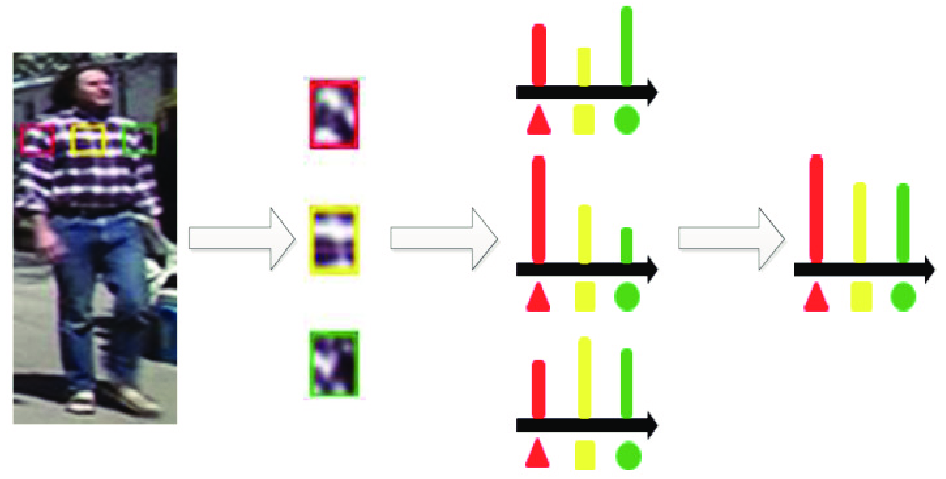
|
图 3 滑动子窗口提取特征示意图 |
不同摄像机中行人视角的变化主要集中在水平方向上, 而在垂直方向上并不很明显. 因此, 该文提取的特征对于水平方向的移动具有一定的不变性. 为了说明本文提出的通过学习一个双向关系相似度函数, 来计算一对行人图像的相似度的优越性. 即使采用比较简单的特征来描述行人图像, 算法性能也能优于一般的度量学习算法, 后续的实验结果也会有所证明.
2.2 BRSF学习为了提高特征的有效性, 便于BRSF的学习, 实验中首先利用PCA (Principle Component Analysis)降维, 在两个数据集的行人图像的特征维数进行降维, 都保持95%以上的能量. 在训练阶段, 利用数据集离线学习得到一个BRSF. 当计算出BRSF的自相关矩阵A和互相关矩阵B, 则根据式(2)计算一对行人图像(i, j)的相似度.
2.3 查询目标行人图像行人再识别的研究目的是在不重叠的多摄像机视频监控系统中, 根据输入的目标行人图像, 检索该行人是否出现在这些视频中. 该文假设通过行人检测技术, 已经将监控视频的行人转换为行人图像库. 利用离线学习得到的BRSF, 度量目标行人图像和行人图像库中所有图像的相似度. 行人图像库中相似度高的图像为潜在的目标行人图像.
3 实验分析算法通过大量的实验来测试, 分别在VIPeR数据集[15]和QMUL GRID数据集[16]上进行了实验对比. 实验中, 随机选择t对行人图像对作为训练样本集, 余下的行人图像对作为测试样本集. 相机A中的行人图像作为查询目标库, 相机B中的行人图像作为候选目标库. 每对行人图像, 任意选择一张图像加入查询目标库, 另一张则加入候选目标库. 每个查询目标库与候选目标库中的每张行人图像都要有匹配. 然后, 再交换查询目标库和候选目标库. 为了得到稳定的实验结果, 以上过程重复10次, 并将10次实验的平均值作为最终的实验结果. 实验结果采用标准的累积匹配特性(Cumulative Match Characteristic, CMC)曲线评价算法性能, CMC是指在候选目标库中匹配待查询的目标, 前r个匹配结果中包含正确匹配结果的比率. 其中, 第一匹配率(Rank=1)为真正的识别能力, 所以比较重要. 但是当Rank值很小时, 也是可以通过人眼进行辅助识别查找目标, 因此也具有现实意义.
3.1 VIPeR数据集的实验结果VIPeR数据集是行人再识别领域最常用的且最具有挑战性的数据集之一. 它包含了632对行人图像, 每对行人图像都是由两个不重叠视角的摄像机在不同的室外环境下获取的. 在632对行人图像中存在着许多视角, 亮度, 背景有着较大变化的图像对. 图4展示了在该数据集上, 待查询图像和候选目标库中与其匹配的图像. 在这两个实验中, 最左边的行人图像为目标图像, 右边的行人图像为候选目标库中根据相似度高低从左到右排序, 其中虚线框内的行人图像为正确的匹配图像. 图5展示了基于MSF和基于BRSF在候选目标库匹配待查询目标的实验结果, 从图5中可以看出基于BRSF在相似度排序中的正确匹配图像比基于MSF的更加靠前了.

|
图 4 本文算法在VIPeR数据集上的实验结果 |
实验中测试样本集和训练样本集均为316对行人图像. VIPeR数据集上的其他实验, 如果没有明确说明测试集和训练集的个数, 则都默认为316对行人图像. 表1给出了本文算法与已有算法的性能比较的实验结果的数据.

|
图 5 基于MSF和基于BRSF在VIPeR数据集上的实验结果 |
| 表 1 VIPeR数据集上本文算法与已有算法性能对比实验结果(训练集样本规模t=316对图像)(单位: %) |
从表1可知, 本文算法性能有较大的提升, 尤其是Rank1比表中排第二的XQDA算法提升了约13.2%, 并且在Rank20内都有着较高的识别率. 在一定程度上, 本文算法的效果已经能够应用到工程实践中, 尤其是在刑事侦查等方面, 刑侦人员可以在行人再识别返回的前r个结果中快速搜索出目标行人, 大大提高侦查办案效率.
当训练集规模为t=200时, 本文算法与已有算法的性能对比结果如表2.
从表2中可知, 在只有少量训练样本情况下, 本文算法同样优于已有算法. 由此可见, 本文算法有效的解决了学习相似度度量函数中出现过拟合的问题.
| 表 2 当训练集样本规模为t=200时, 本文算法与已有算法在VIPeR数据集上性能对比的实验结果(单位: %) |
为了说明本文提出的BRSF算法的优越性, 表3给出了本文算法仅用一种特征情况下与其他算法效果对比. 由于表中对比的算法都有HSV颜色空间特征和LBP纹理特征, 因此实验中分别选用HSV和LBP作为BRSF算法提取的特征.
| 表 3 仅用一种特征情况下的BRSF算法与已有算法性能比较实验结果(单位: %) |
由表3可知, 该算法虽然只使用了一种特征, 但是效果比其他采用多特征的算法更好. 其中, RPLM算法融合了HSV、Lab和LBP等特征, Rank1仅有27.0%. 而本文算法只用了HSV颜色特征, Rank1就达到了47.4%. 当本文算法用到多特征时, 算法的识别率又提升了一些, 但是继续增加特征, 算法识别率提升的幅度会越来越小, 而算法的时间复杂度会越来越高. 因此, 本文算法在最终的特征选择上只选用了三种颜色空间特征和一种纹理特征.
评价度量学习算法性能好坏的一个重要因素是训练时间的长短, 本文提出的BRSF算法是在基于KISSME度量学习算法上进行训练的, 省略了迭代优化的时间, 从而减少了训练时间. 本文实验平台是8 GB内存, Intel i5-2400 3.1 GHz CPU的PC台式机, 实验环境是基于Matlab 2014b实验的. 表4给出了本文算法与已有度量学习算法的训练时间比较实验结果, 实验结果是取10组在VIPeR数据集上的训练时间的平均值.
| 表 4 本文算法与已有算法的训练时间对比实验结果 |
从表4可知, 本文算法训练时间比其他大部分算法的耗时要短, 只比KISSME算法耗时多了一些, 因为KISSME训练得到MSF的一个矩阵, 而本文算法基于KISSME上训练得到BRSF的两个矩阵, 一个自相关矩阵, 一个互相关矩阵.
3.2 QMUL GRID数据集的实验结果QMUL GRID数据集是目前行人再识别领域难度最高的数据集. QMUL GRID数据集上的图片是从地铁站的8个不相交的摄像机中拍摄获取的, 其中包含了250对行人图像. 除此之外, 该数据集中还包含了额外的775张行人图像, 这775张行人图像不属于250对行人图像中的任何一个行人, 扩展了候选目标库. 上述这些都体现了该数据集测试行人再识别的难度所在. 图6展示了QMUL GRID数据集上的一些行人图像对样本.

|
图 6 QMUL GRID数据集上的5对行人图像对 |
从图6中可以看到这些行人图像的图像质量, 分辨率低, 并包含了大量的照明和视角的变化. 在QMUL GRID数据集的实验上, 我们随机选择125对行人图像作为训练集, 剩下的125对和额外的775张行人图像作为测试集. 表5给出了本文算法在QMUL GRID数据集上与其他算法的比较实验结果. 从表5可知, 所有算法的识别率都不是特别高, 但是本文算法的Rank1比表中排第二的XQDA算法提升了约7%, 并且本文算法的Rank10和Rank20比其他算法都有着显著的提升.
| 表 5 QMUL GRID数据集本上文算法与已有算法性能对比实验结果(单位: %) |
4 结论
行人再识别是一个具有很高应用价值同时也更具有挑战性的技术. 提出了一种通过学习一个双向关系相似度函数, 来计算一对行人图像的相似度. BRSF是MSF的泛化形式, 与MSF相比, BRSF引入了一对行人的自相关关系和互相关关系, 从而可以更好地捕捉同一个人在不同摄像机下的外观变化. 为了学习BRSF, 借助了KISSME的度量学习思想, 把最终高斯分布的比值转换为BRSF的形式, 得到一个对背景、视角、姿势的变化具有鲁棒性的相似度函数. 由行人再识别的公共数据集VIPeR和QMUL GRID上的实验结果表明, 基于双向关系度量学习得到有效的相似度函数, 识别性能优于已有的行人再识别算法.
| [1] |
Li Z, Chang SY, Liang F, et al. Learning locally-adaptive decision functions for person verification. Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, OR, USA. 2013. 3610–3617.
|
| [2] |
Gong SG, Cristani M, Yan SC, et al. Person Re-identification. London: Springer, 2013. 301–313.
|
| [3] |
Farenzena M, Bazzani L, Perina A, et al. Person re-identification by symmetry-driven accumulation of local features. Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). San Francisco, CA, USA. 2010. 2360–2367.
|
| [4] |
Wang XY, Yang M, Zhu SH, et al. Regionlets for generic object detection. Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, NSW, Australia. 2013. 17–24.
|
| [5] |
Liao SC, Hu Y, Zhu XY, et al. Person re-identification by local maximal occurrence representation and metric learning. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA. 2015. 2197–2206.
|
| [6] |
Liu Y, Shao Y, Sun FC. Person re-identification based on visual saliency. Proceedings of the 12th International Conference on Intelligent Systems Design and Applications. Kochi, India. 2012. 884–889.
|
| [7] |
Zhao R, Ouyang WL, Wang XG. Person re-identification by salience matching. Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, NSW, Australia. 2013. 2528–2535.
|
| [8] |
Luo Y, Jiang M, Wong YK, et al. Multi-camera saliency. IEEE Transactions on Pattern Analysis and Machine Intelli-gence, 2015, 37(10): 2057-2070. DOI:10.1109/TPAMI.2015.2392783 |
| [9] |
陈莹, 霍中花. 多方向显著性权值学习的行人再识别. 中国图象图形学报, 2015, 20(12): 1674-1683. DOI:10.11834/jig.20151212 |
| [10] |
Xing EP, Ng AY, Jordan MI, et al. Distance metric learning, with application to clustering with side-information. Proceedings of the 15th International Conference on Neural Information Processing Systems. Cambridge, MA, USA. 2003. 505–512.
|
| [11] |
Zheng WS, Gong SG, Xiang T. Person re-identification by probabilistic relative distance comparison. Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Colorado Springs, CO, USA. 2011. 649–656.
|
| [12] |
Köstinger M, Hirzer M, Wohlhart P, et al. Large scale metric learning from equivalence constraints. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA. 2012. 2288–2295.
|
| [13] |
齐美彬, 檀胜顺, 王运侠, 等. 基于多特征子空间与核学习的行人再识别. 自动化学报, 2016, 42(2): 299-308. |
| [14] |
Liao SC, Zhao GY, Kellokumpu V, et al. Modeling pixel process with scale invariant local patterns for background subtraction in complex scenes. Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, CA, USA. 2010. 1301–1306.
|
| [15] |
Gray D, Tao H. Viewpoint invariant pedestrian recognition with an ensemble of localized features. Proceedings of the 10th European Conference on Computer Vision. Marseille, France. 2008. 262–275.
|
| [16] |
Loy CC, Xiang T, Gong SG. Multi-camera activity correlation analysis. Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami, FL, USA. 2009. 1988–1995.
|
| [17] |
Hirzer M, Roth PM, Köstinger M, et al. Relaxed pairwise learned metric for person re-identification. Proceedings of the 12th European Conference on Computer Vision. Florence, Italy. 2012. 780–793.
|
| [18] |
Xiong F, Gou MR, Camps O, et al. Person re-identification using kernel-based metric learning methods. Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland. 2014. 1–16.
|
| [19] |
Mignon A, Jurie F. PCCA: A new approach for distance learning from sparse pairwise constraints. Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA. 2012. 2666–2672.
|
 2018, Vol. 27
2018, Vol. 27


