2. 华中科技大学 计算机科学与技术学院, 武汉 430074;
3. 中山大学 信息科学与技术学院, 广州 510006
2. School of Computer Science and Technology, Huazhong University of Science & Technology, Wuhan 430074, China;
3. School of Information Science & Technology, Sun Yat-Sen University, Guangzhou 510006, China
当今社会, 基于互联网技术的电子商务不断普及, 大数据分析和大数据挖掘已成为迫切要解决的问题. 推荐系统是指根据用户的兴趣特点和购买行为, 向用户推荐用户感兴趣的信息和商品的系统. 其中协同过滤推荐(collaborative filtering recommendation)是推荐系统中应用最早和最为成功的技术之一, 它一般采用最近邻技术, 利用用户的历史喜好信息计算用户之间的距离, 然后 利用目标用户的最近邻居用户对商品评价的加权评价值来预测目标用户对特定商品的喜好程度, 系统从而根据这一喜好程度来对目标用户进行推荐. 协同过滤最大优 点是对推荐对象没有特殊的要求, 能处理非结构化的复杂对象, 如音乐、电影等媒体数据[1]. 其中的潜在因素模型(latent factor models)的核心思想是: 通过分析历史数据来预测事物的发展趋势, 矩阵分解算法(matrix factorization)是其中最为成功的算法之一[2]. 但随着互联网数据的不断扩大, 应用传统的矩阵分解算法构造大数据潜在因素模型, 算法性能会大大下降, 难以实现有效的协同过滤, 其关键问题体现在数据稀疏性和算法可扩展性的改进上.
针对上述问题, 国内外学者专家们提出了一些改进想法: Pilaszy I最先提出基于ALS的协同过滤算法, 相对传统算法而言, 能有效提高过滤质量和推荐速度, 但该算法只考虑用户的相似性[3]; 李改等对前者进行改进, 提出了ALS-WR 协同过滤算法, 该算法考滤到可扩展性方面, 但需要专门设计迭代式算法[4]; 王辉等把用户聚类思想引入到协同过滤算法中, 改进了传统算法的数据稀疏性和可扩展性, 但精确度较低[5] .
本文提出一种基于BC-AW的协同过滤推荐算法, 在传统算法的基础上, 引入联合聚类BC(BlockClust)和正则化迭代最小二乘法(Alternating least squares with Weighted regularization, AW). 首先分解原始评分矩阵的用户项目双维度, 然后使用联合聚类计算出多个同类评分块的子矩阵, 最后使用正则化迭代最小二乘法预测各个子矩阵的未知评分, 从而计算出推荐结果. 使用联合聚类所求得的子矩阵远比初此矩阵规模小, 可以大大减少过滤推荐的计算量. 通过与BaseMF算法、RSTE算法、TidaTrust算法、MoleTrust算法进行对比实验, 分析结果表明, 本文算法可以有效缓解传统算法并行化、可扩展性差的问题.
1 AW算法设定矩阵
Step1: 我们通过最小化Frobenius的损失函数来算出一个低秩矩阵
| ${ L}({\rm X}) = {\sum\nolimits_{{ij}} ({ R}_{{ij}} - { X}_{{ij}})^2} $ | (1) |
上述公式(1)中,
Step 2: 求解
| $L({rm U,V}) = {\sum\nolimits_{ij} {({R_{ij}} - {U_i}{V_j}^{\rm T})} ^2}$ | (2) |
上述式(2)会产生过于拟合的问题, 因此需要通过正则化项来解决这个问题, 则改写如下:
| ${{L}}\left( {{\rm {U}},{\rm {V}}} \right) = \mathop \sum \limits_{{{ij}}} {\left( {{{{R}}_{{{ij}}}} - {{{U}}_{{i}}}{{V}}_{{j}}^{\rm{T}}} \right)^2} + \lambda \left( {{{{U}}_{{i}}}_{{F}}^2 + {{{V}}_{{j}}}_{{F}}^2} \right)$ | (3) |
Step3: 对上面公式(3), 设定
| ${U_i} = {R_i}{V_{ui}}{(V_{ui}^{\rm T}{V_{ui}} + \lambda {n_{ui}}I)^{ - 1}},\;i \in [1,m]$ | (4) |
公式(4)中,
Step4: 上述对公式(4)中, 设定
| ${V_j} = R_j^{\rm T}{U_{mj}}{(U_{mj}^{\rm T}{U_{mj}} + \lambda {n_{mj}}{\rm I})^{ - 1}},\;j \in [1,m]$ | (5) |
上述公式(5)中,
BC算法能够将用多个较小且高相似度的评分矩阵来替代原始数据[7]. 通过扫描该矩阵中的评分, 使用聚类方法计算行和列, 计算一次后, 重新评估每个子矩阵中用户、项目的概率, 如此类推, 直到产生收敛为止[8]. 然后将评分匹配到最大概率的子矩阵中. 其算法思想如下:
首先扫描评分矩阵, 通过计算各评分的所属概率
| $p(k|u,v,r) = \frac{{(p(k|u) + \alpha ) \times (p(k|v) + \beta ) \times (p(r|k) + \theta )}}{{\sum\nolimits_{{k'} \in k} {(p({k'}|u) + a) \times (p({k'}|v) + \beta ) \times (p(r|{k'} + \theta ))} }}$ | (6) |
| $p(k|u) = \frac{{\sum\nolimits_{V \in V(u)} {p(k|u,v,r)} }}{{\sum\nolimits_{{k'} \in k} {\sum\nolimits_{V \in V(u)} {p({k'}|u,v,r)} } }}$ | (7) |
| $p(k|v) = \frac{{\sum\nolimits_{u \in U(V)} {p(k|u,v,r)} }}{{\sum\nolimits_{{k'} \in k} {\sum\nolimits_{u \in U(V)} {p({k'}|u,v,r)} } }}$ | (8) |
| $p(r|k) = \frac{{\sum\nolimits_p {(k|u,v,r)} }}{{\sum\nolimits_{{r'}} {\sum\nolimits_{V \in U(V)} {p({k'}|u,v,r)} } }}$ | (9) |
以上公式中,
以下通过联合聚类和AW协同过滤两阶段来对评分矩阵的未知项进行预测.
1) 联合聚类
输入: 子矩阵个数
输出: 子矩阵数
Step1:
Step2: 应用公式(7)计算用户
Step3: 最后选择概率
Step4: 跳回步骤2, 直到出现收敛, 结束循环.
2) AW协同过滤
首先用偏差小于等于的高斯随机数初始化矩阵
输出: 用户评分矩阵
输出:
Step1: 用偏差小于等于0.01的高斯随机数初始化
Step2: 分别用公式(4)和公式(5)更新
Step3: 重复迭代公式(4)、公式(5), 判断得出的RMSE值是否收敛, 如果是, 则迭代结束;
Step4: 令
下面我们分析该算法的时间复杂度: 设
综上所述, 本文基于矩阵分解的BC-AW协同过滤推荐算法改进传统算法的串行运算方式, 实现并行运算, 可以有效地解决传统算法中存在的可扩展性差问题.
4 实验分析 4.1 数据准备本实验目的是通过分析比较本文算法和传统算法的性能, 硬件方面选用基于云计算的分布式硬件实验平台, 该平台由20台电脑组成20个运算节点, 每个节点配有 4.0 Hz的Intel处理器和32 G的内存, Linux操作系统. 实验数据来自美国Minnesota大学GroupLens项目组的MovieLens数据集. MovieLens数据集是GroupLens项目组开发的一个互联网研究型推荐系统数据集. MovieLens数据集中含有943个用户对1682部电影的100 000条评分数据, 平均每个用户评分的电影大于等于20部[10].
4.2 评价指标本次实验采用均方根误差RMSE和评分覆盖率
| $RMSE = \sqrt {\sum\nolimits_{(u,i)|{R_{\rm test}}} {{{({r_{ui}} - {{\widehat r}_{ui}})}^2}/{R_{\rm test}}} } $ | (12) |
其中
| $CO{V_R} = \frac{{\text{可预测的评分数}}}{{\text{整个测试集的评分个数}}}$ | (13) |
本文算法分别与BaseMF (基于矩阵分解算法) [12]; RSTE (概率矩阵分解算法) [13]; TidaTrust (基于TidaTrust模型推荐算法) [14]; MoleTrust (基于MoleTrust模型推荐算法) [15]这4种推荐方法通过分析RMSE和
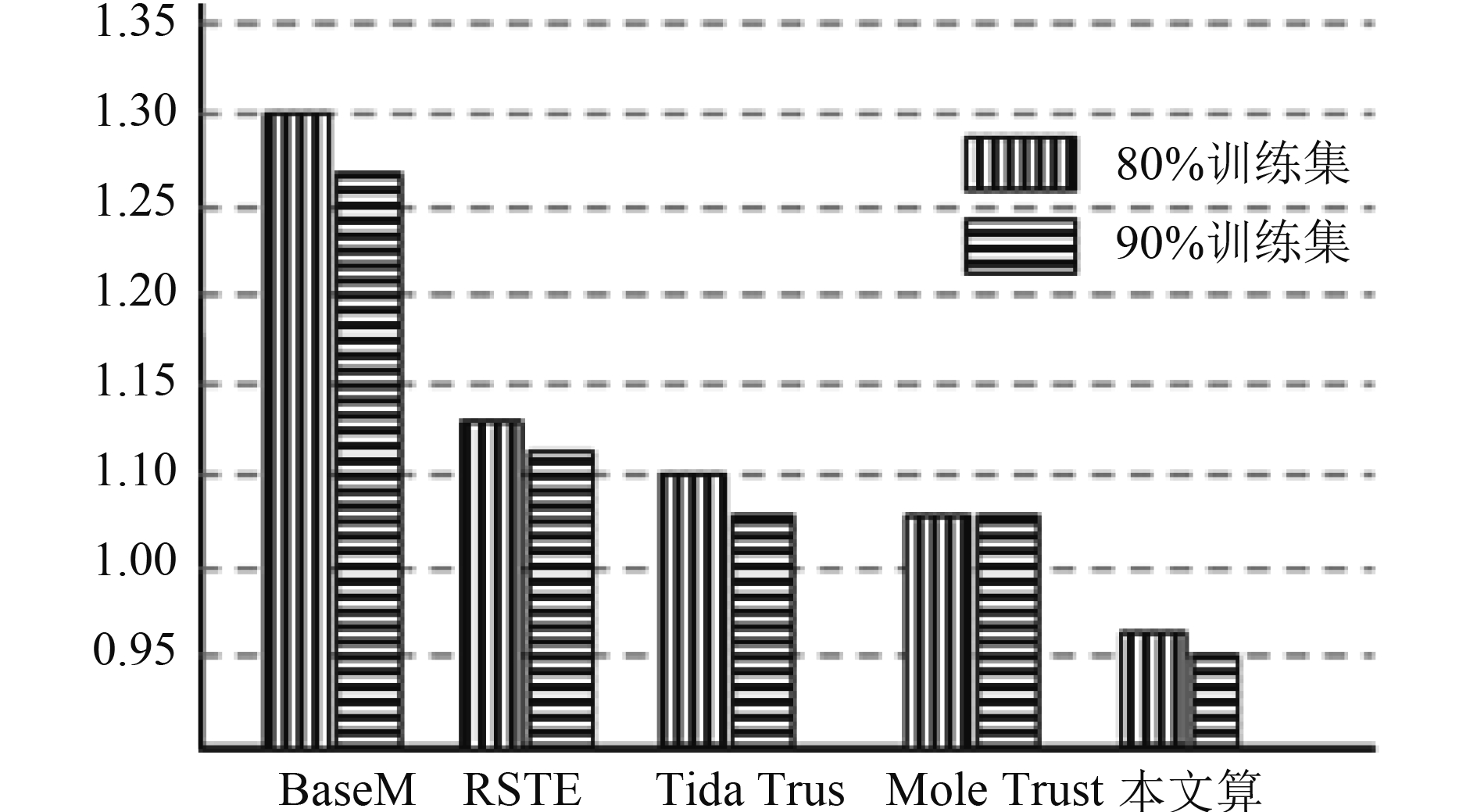
|
图 1 5种算法的RMSE值比较图 |
从上图可以看出, 针对RMSE值, 当训练集为80%时, 本文算法比BaseMF算法降低了22%, 比RSTE算法降低了11%, 比TidaTrust算法降低了8%, 比MoleTrust 算法降低了7%; 当训练集为90%, 本文算法比BaseMF算法降低了21%, 比RSTE算法降低了10%, 比TidaTrust算法降低了7%, 比MoleTrust算法降低了7%; 由此可知, 本文算法的误差值明显低于传统的4种推荐算法.
图2(a)、图2(b)分别表示本文算法在GROUP1、GROUP2这两组训练集中, RMSE在不同
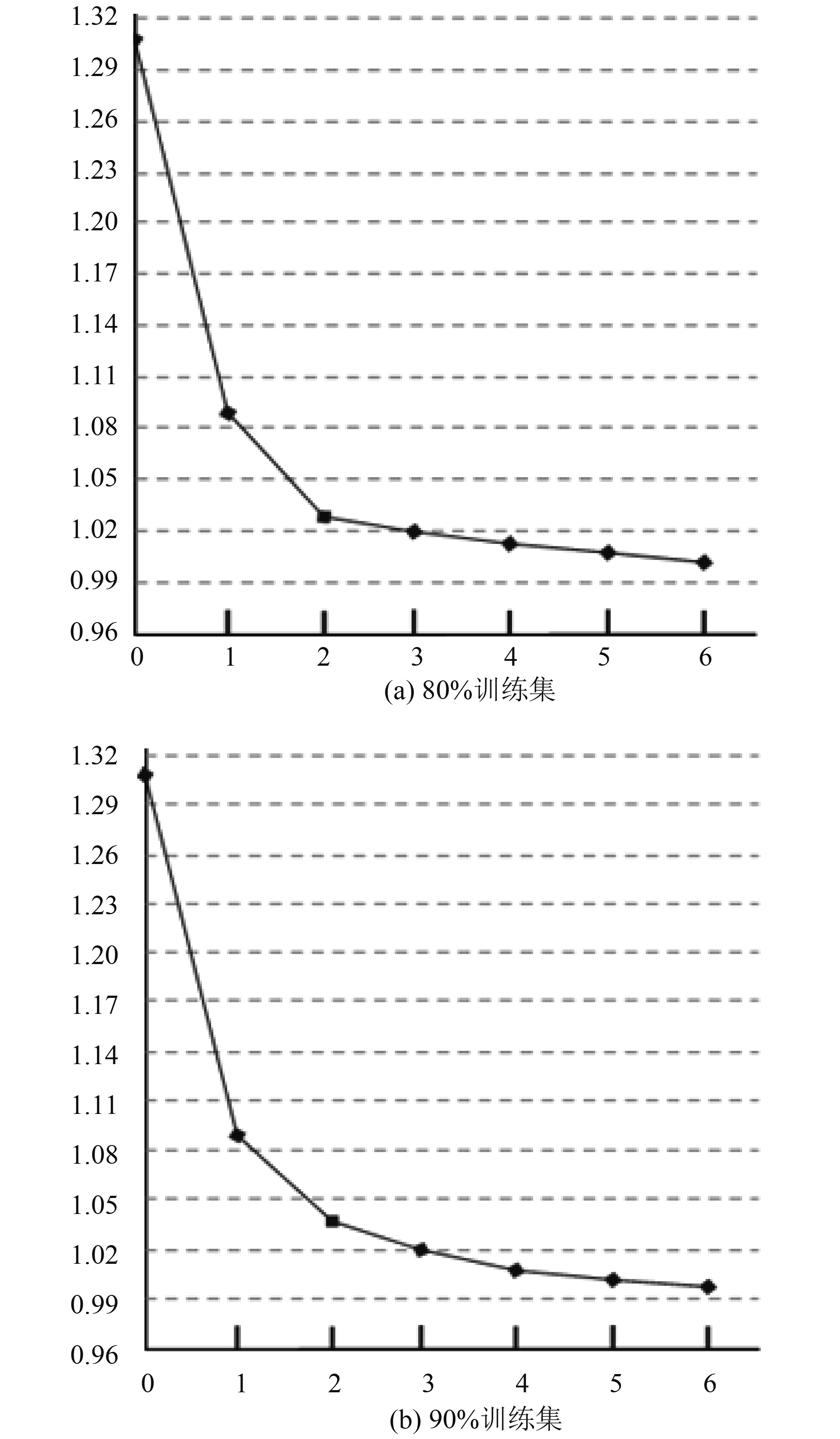
|
图 2 RMSE随参数的变化曲线 |
下面分析5种算法的
| 表 1 5种算法的COVR |
分析表1可以看出, 当训练集为80%时, 本文算法的
本文针对现有协同过滤算法中普遍存在的数据稀疏、可扩展性低这两个核心问题, 提出BC-AW(基于联合聚类和迭代最小二乘法)两阶段协同过滤算法. 首先由该算法通过对原评分矩阵进行用户—项目双维度联合聚类后得到的若干个子矩阵(这些子矩阵均为模式相同的评分块), 其规模比原矩阵小得多, 因此可以有效减少预测工作量; 再者, 采用正则化迭代最小二乘法预测子矩阵的未知评分可以优化推荐效率. 该算法在模拟大数据实验中(美国Minnesota大学GroupLens项目组的MovieLens数据集), 通过与几个经典的协同过滤算法(BaseMF算法、RSTE算法、TidaTrust、MoleTrust算法)作比较. 实验结果表明, 本文算法能有效改进推荐系统的稀疏性、可扩展性问题, 系统预测评分与用户实际评分接近, 并能为用户提供良好的使用体验.
| [1] |
Shuo LX, Chai BF, Zhang XD. Collaborative filtering algorithm based on improved nearest neighbors. Computer Engineering and Applications, 2015, 51(5): 137-141. |
| [2] |
Zhang HJ. The research and application of distributed matrix factorization algorithm in recommend system. Bulletin of Science and Technology, 2013, 29(12): 151-153. |
| [3] |
Wang QM, Miao Y, He M, et al. Parallelized research on collaborative filtering algorithm based on matrix factorization. Computer Technology and Development, 2015, 25(2): 55-59. |
| [4] |
Zhu X, Song AB, Dong F, et al. A collaborative filtering recommendation mechanism for cloud computing. Journal of Computer Research and Development, 2014, 51(10): 2255-2269. |
| [5] |
Bi XR. Collaboration filtering recommendation algorithm of sub-similarity integration between items. Computer Systems & Applications, 2015, 24(1): 147-150. |
| [6] |
Wang L, Fu XF, Wang XM. Hybrid dynamic collaborative filtering algorithm based on big data sets. Journal of Guangdong University of Technology, 2014, 31(3): 44-48. |
| [7] |
Chen W, Shi QL. An adaptive algorithm for collaborative filtering recommendation. Journal of Xianyang Normal University, 2014, 29(6): 47-49. |
| [8] |
Li G, Li L. One-class collaborative filtering based on matrix factorization. Application Research of Computers, 2012, 29(5): 1662-1665. |
| [9] |
Ke LW, Wang J. Collaborative filtering recommendation based on user feature transfer. Computer Engineering, 2015, 41(1): 37-43. |
| [10] |
Yi ZA, Mu CM. Collaborative filtering algorithm based on subtractive clustering and genetic fuzzy. Computer & Digital Engineering, 2014, 42(8): 1363-1367. |
| [11] |
Xu W, Duan F. Combining clustering and collaborative filtering for implicit recommender system. Computer Engineering and Design, 2014, 35(12): 4181-4185. |
| [12] |
Liu L. A collaborative filtering recommender algorithm based on iterative kernel method. Information Technology & Informatization, 2014(12): 76-81. |
| [13] |
Zha J, Li ZB, Xu GQ. An optimised collaborative filtering algorithm based on combined similarity. Computer Applications and Software, 2014, 31(12): 323-328. |
| [14] |
Wu HC, Wang XJ, Cheng Y, et al. Advanced recommendation based on collaborative filtering and partition clustering. Journal of Computer Research and Development, 2011, 48(S3): 205-212. |
| [15] |
Luo Q, Miao XJ, Wei Q. Further research on collaborative filtering algorithm for sparse data. Computer Science, 2014, 41(6): 264-268. |
 2018, Vol. 27
2018, Vol. 27


