无人机是一种利用无线电遥控无人机和利用自我控制程序控制装置操纵的不载人飞机[1]. 无人机由于体积小、重量轻、隐藏性好、价格低廉、操作简单, 目前在军用和民用方面得到了广泛的应用. 在军事应用中, 无人机可以通过使用光电传感器, 机载雷达和机载武器系统装备不同的军事设备[2]. 它也适用于民用领域, 包括数据收集、人员搜救、农作物监测、资源勘查等[3–7]. 无人机的摄像头捕捉到空中目标或者地面目标以后, 将捕捉的画面传送给空中无人机群或者地面接收人员. 这就需要设计图像传输系统的编码、传输、接收和解码. 在某些特定的应用场景下, 将无人机传输的图像作为飞行控制和导航的关键信息, 需要较高的可靠性保障.
传统的无人机与地面接收机之间的信道编码采用Turbo码、LDPC码等. Turbo码和LDPC码译码复杂、实时性较差, 硬件成本高, 其中LDPC码在高信噪比时易导致错误地板. 如何设计一个简单有效的译码器是目前Turbo码在无人机测控系统中实用化研究的重点[8]. 格雷码码长短, 能量高, 运算时间少, 在硬件实现上, 设备量少, 体积小, 重量轻, 功耗更低, 适合无人机的负载和能量有限的要求. 本文首次提出采用格雷码应用至无人机信息传输中, 基于格雷码在比特纠错基础上, 降低了运算的复杂度, 在其可纠错能力范围内可保证信息的正确性, 且可杜绝地板错误发生的情形. 并将其改良为依据奇偶校验位选择不同的译码判决机制, 能够配合数据传输精度的需求, 采用最合适的解码方法以较快的速度达到使用者的精度需求.
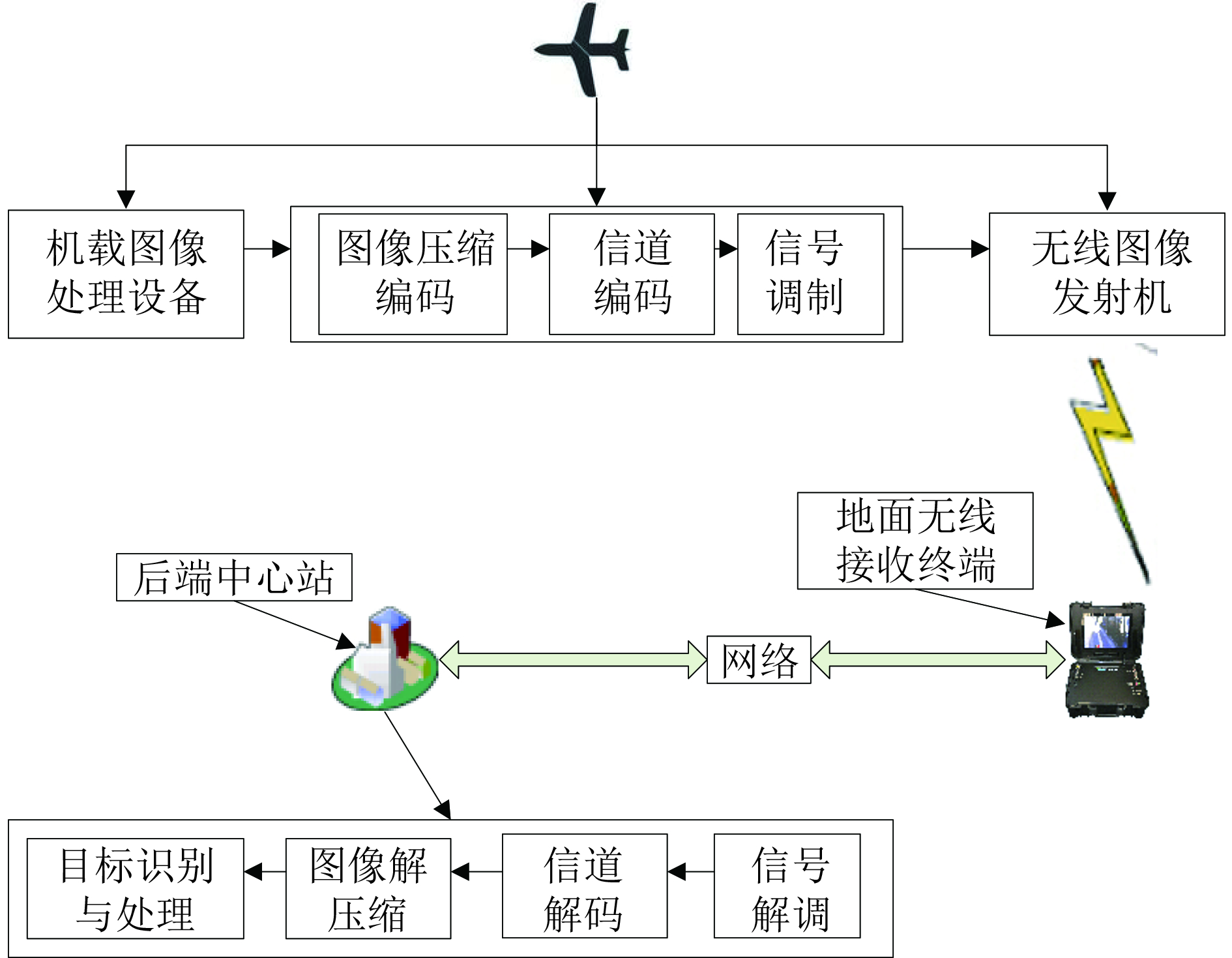
1 无人机图像传输系统模型 1.1 基于格雷码的无人机图像传输系统在无人机图像传输系统中, 采用格雷码可以提高图像传输系统的可靠性. 无人机图像传输系统中格雷码图传系统模型如图1所示. 无人机通信信道是一个非常复杂的动态信道. 信号从发射机发射出去到接收机接收的过程中, 会经历不同的路径. 不同的路径拥有不同的信号干扰, 会导致信号在传输过程发生不同的变化, 接收机接收到多个不同版本的信号. 无人机通信系统中分为上行和下行信道. 所谓上行, 即从地面往空间发送信号, 下行就是从空中平台向地面发送信号[9]. 图1 中所示的无人机发射部分和地面站接收部分上各有一套系统来完成测控信息的传输. 无人机测控数据在发送端经过编码、加密、格雷码信道编码后通过扩频和某种方式的调制后进行无线传播. 在接收端经过解扩、解调、信道译码后, 解码恢复并获取数据.
2 自适应译码算法原理 2.1 格雷码算法原理格雷码为平方剩余码, 其码率略大于或等于0.5且有着较大的最小距离, 因此纠错性能优异. 其中扩展码型(24, 12, 8)格雷码已经被广泛应用于通信系统中, 包括美国NASA的Voyager图像系统. 扩展格雷码的编解码原理如下所示.
|
图 1 格雷码图传系统模型 |
扩展格雷码对任意的输入12位元的信息位m进行编码, 即将输入信息m和生成多项式g相乘得到码字c0, 再将c0的最低位后加上奇偶校验值构成扩展格雷码c. 在传输过程中会发生噪声e干扰, 而接收者接收到的码字r就是c与e相加的结果. 然后我们对接收到的r进行解码处理, 在硬判决纠错能力范围内可得到原有码字c及输入信息m.
软判决译码原理如下:
第1步: 根据软判决接收序列r做硬判决得到序列z;
第2步: 基于软判决接收序列r的LRP组, 构造错误模式集合E;
第3步: 用错误模式集合E中的每一个错误图案e对硬判决序列z进行修改, 得到修改后的接收向量z+e;
第4步: 使用硬判决译码器将修改后的向量z+e译为码字集合C中的一个码字(当然也可能由于z+e的错误个数大于码的纠错能力t, 而导致译码失败);
第5步: 根据第4步得到码字生成一个候选码字表, 计算列表中每个码字的软判决译码度量, 若使用的度量是相关, 则找到度量值最大的码字, 若使用的是相关差, 则找取度量值最小的码字, 以此码字为译码结果[10].
本文的格雷码硬判决译码算法采用扩展格雷码硬判决译码算法, 它能够纠正24位分位码组中的任何3个或者更少的随机差错的组合, 软判决译码算法采用格雷码软判决译码算法, 它能够纠正23位分位码组中的任何6个或者更少的随机差错的组合.
2.2 自适应译码算法 2.2.1 算法的提出本文提出基于格雷码的无人机图像传输自适应译码算法, 主要基于格雷码译码复杂度远低于Turbo码译码复杂度.
Turbo码的SOVA译码算法时间复杂度为:
| $T({{m}}) = 3\left( {m + 1} \right) + {2^m} + 2*{2^m}{\rm{ + }}6\left( {{{m}} + 1} \right) + 8$ | (1) |
| ${\text{即}}T({{m}}) = {\rm O}({2^m})$ | (2) |
m为Turbo码译码算法的码字. Turbo码的交织器的长度对其性能影响很大. 一般情况下信息序列分组长度和交织器的大小相同. 交织长度的增加可以提高Turbo码的性能, 但随着信息序列长度的增加, 译码的复杂性也随之增大, 这样会带来较大时延, 在实际应用中一般选用1024 bits较为合适. 因此, 在这里我们可以取Turbo码译码时间复杂度为:
| $T(1024) = {2^{1024}}$ | (3) |
格雷码的算法时间复杂度为
| $T({{n}}) = T(n - 1) + {\rm O}(n{*2^n}),(n > 1)$ | (4) |
| ${\text{即}}T({{n}}) = {\rm O}(n*{2^n}).$ | (5) |
n为格雷码译码算法的码字, 其码字长度为23, 因此, 其时间复杂度为:
| $T(23) = 23*{2^{23}}$ | (6) |
比较公式(3)和(6), Turbo码的时间复杂度接近是格雷码的1.4*2996倍, 因此, 选择格雷码作为无人机图像传输的信道编解码可以解决Turbo码译码的时间复杂度较大这个问题, 具有显著的优势.
2.2.2 通过奇偶校验权衡译码精度和速度本文提出通过奇偶校验位权衡译码精度和速度, 主要基于格雷码的硬判决解码速度远快于软判决, 但译码精度远低于软判决.
在23位分位码组中, 格雷码硬判决最大纠错能力为3 bits, 当数据出现3 bits以上错误的时候, 其无法纠出, 这样就影响了数据的精度, 导致地面接收站无法更加精准的还原出图片, 稍有损耗无人机图像传输的可靠性, 但其速度更快. 此原理同样适合扩展格雷码硬判决. 格雷码软判决最大纠错能力为6 bits, 具有较强的纠错能力, 其精度更加精准, 还原的图片更加清晰, 但是其速度相对较慢, 稍有损耗无人机图像传输的实时性. 这是因为格雷码的软判决译码算法根据软判决接收序列r得到硬判决接收序列z, 并对r向量的每个分量取绝对值作为z相应位置上的可靠性值. 根据可靠性值, 考虑取z的
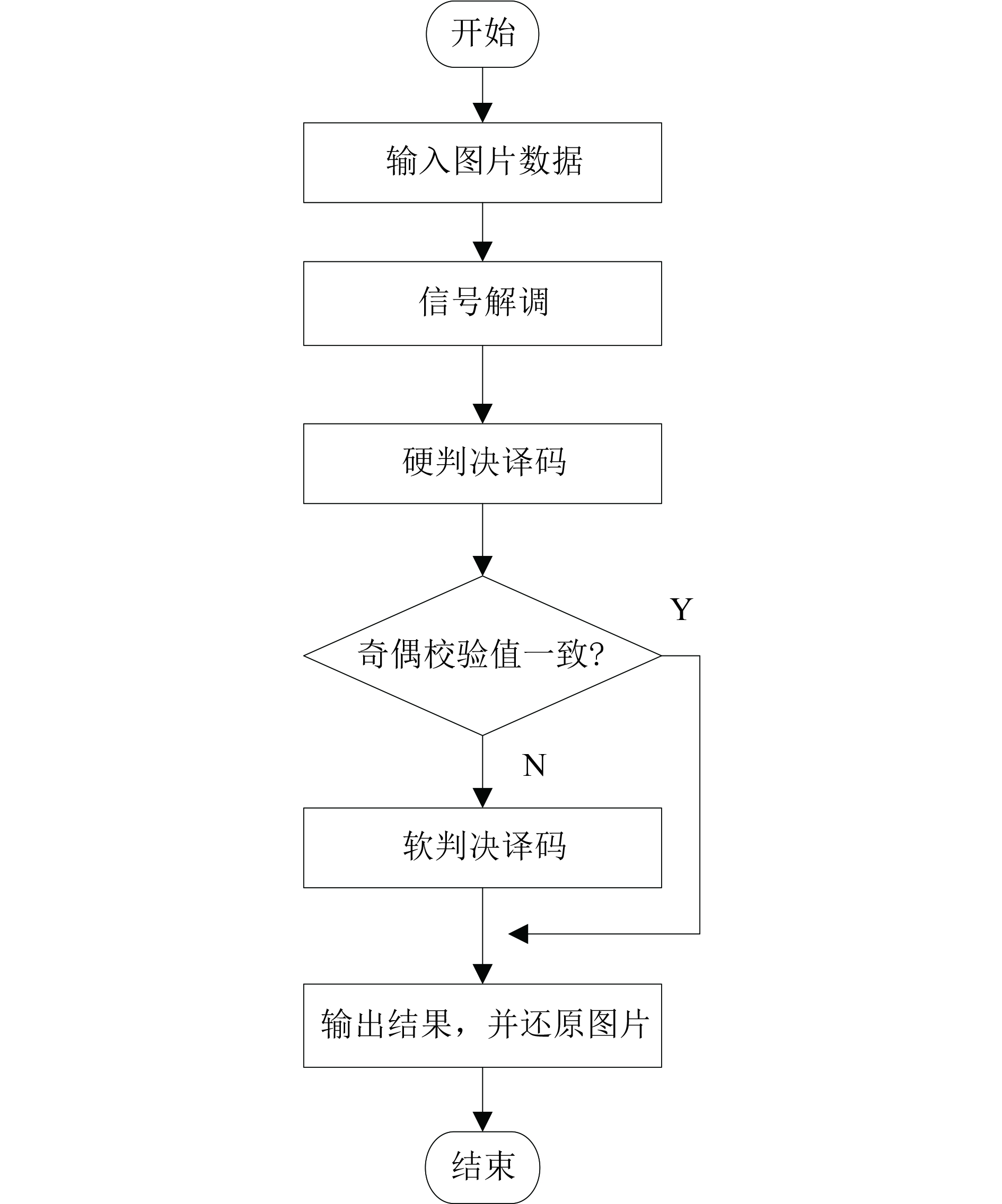
为了降低图像译码时延, 提高译码的实时性, 同时也兼顾到图像译码的精度, 本文提出通过奇偶校验位来权衡译码精度和速度, 得到的自适应译码流程如图2所示.
|
图 2 自适应译码流程图 |
下文将介绍具体设计.
扩展格雷码是在格雷码的硬判决的基础上适当修正后得出的, 也就是说对格雷码的每一个码子后面加上一个校验元, 并满足以下校验关系:
| ${C_0} \oplus {C_1} \oplus \cdots \oplus {C_{22}} \oplus {C_{23}} = 0$ | (7) |
帧数据经过硬判决解码后, 当码字满足以上0校验关系时, 本文认为此帧数据的错误已经完全解出, 此时直接输出结果, 当不满足以上关系时, 则说明该帧数据还有错误尚未完全解完, 则将数据传输到软判决中去, 利用软判决较强的译码能力, 再对该数据译码.
随机给出一帧数据位为1110 1100 1101 1000 1010 1011, 最后一位为校验位, 此时每位按照公式(7)进行异或, 结果为0. 满足以上校验关系, 本文认为此帧数据受环境干扰的错误全部解出, 直接输出结果. 反之, 若此帧数据最后一位为0, 此时异或结果为1. 不满足以上校验关系, 本文认为此帧数据受环境干扰的错误没有全部解出. 此时将此帧数据的最后一位校验位删除, 然后传输到软判决中去. 当数据经过软判决译码结束后, 直接输出结果. 至此, 该帧数据译码结束.
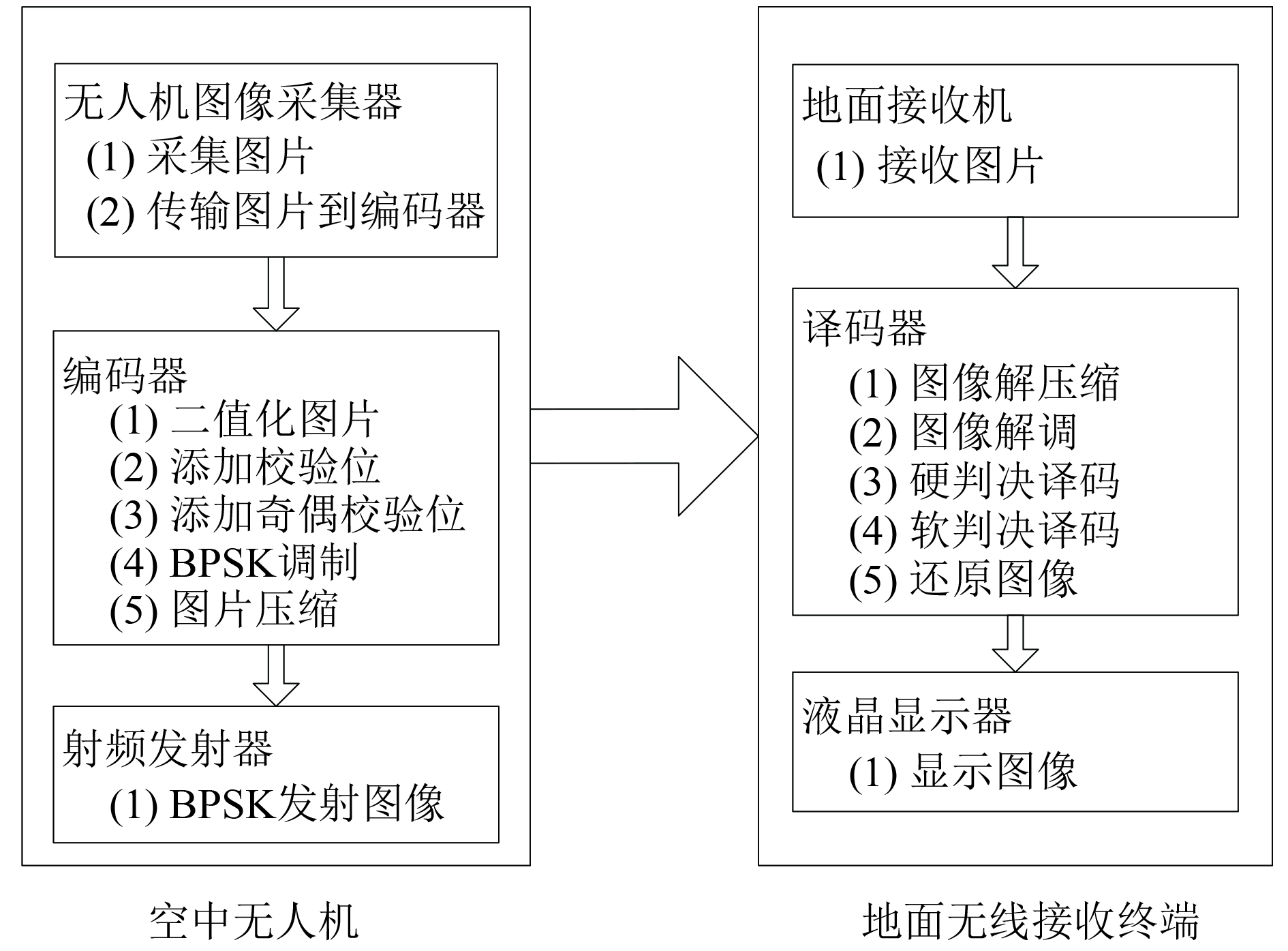
2.2.3 算法应用于无人机空地图像传输本文将提出的格雷码自适应译码算法应用于无人机图像传输, 主要基于2.2.1节和2.2.2节所述内容. 图3 为格雷码自适应译码算法应用于图像处理.
|
图 3 格雷码自适应译码算法应用于图像处理 |
当编码器接收到需要传输的图像数据时, 首先采用自上而下, 自左而右的方式扫描图片, 读取图片的像素值. 每读取一个十进制像素值将其二进制化变成一帧长为12 bits的数据, 并添加校验位以及奇偶校验位变成帧长为24 bits的数据. 接着对这帧数据进行BPSK调制, 调制完成后, 压缩并通过射频发射器将其发射出去. 当接收机接收到这帧数据时, 先将其解压, 解调, 随后开始译码. 先选择格雷码扩展码的硬判决译码方式, 一帧数据译码完成后, 检查奇偶校验位是否一致. 若一致, 则认定该串数据中的错误全部解出, 输出结果; 若不一致, 则将该帧数据去除奇偶校验位, 并输入到格雷码的软判决译码算法中去, 译码完成后, 输出结果. 输出的结果按照提取像素的顺序存于一个图像框内, 将其还原成图像.
3 系统仿真及性能分析 3.1 系统仿真无人机通信信道中存在较强的地面反射波, 因此, 无人机的通信信道是频率选择性的Rayleigh或者Rician慢衰落信道[12]. 同时考虑到Rayleigh信道是Rician信道的特例, 因此无人机信道可用Rician衰落信道模型来表示, 上述两个信道的基础都是在高斯信道分配下加上各自的特性来实现. 所以本文做仿真时, 选择在高斯信道下仿真, 不会失去其一般性. 仿真环境为Intel(R) Core(TM) i5-3470, 4 GB内存, 32位操作系统. 处理的航拍图像来自大疆phantom 3 standard, 具有3000*4000像素, 如图4所示. 该图将在高斯信道中传输, 并比较不同接收信噪比下分别采用未编码算法、Turbo码译码算法、格雷码硬判决译码算法、格雷码软判决译码算法、本文所提出自适应译码算法的误比特率性能(Bit Error Rate, BER). 其中扩展格雷码编码及特性如下. 生成多项式为:
| ${\rm{g}}(x) = \prod {_{i \in {Q_{23}}}} (x - {\beta ^i}) = {x^{11}} + {x^9} + {x^7} + {x^6} + {x^5} + x + 1$ | (8) |

|
图 4 航拍图像(大疆phantom 3 standard, 3000*4000像素) |
信息位为12 bits, 经编码后生成码字帧长为23 bits, 其码率接近1/2, 汉明距离为7, 之后在帧尾加上一位校验位生成扩展格雷码, 码率为1/2, 汉明距离为8. 解码时先对原先的23 bits数据进行硬判决, 若符合校验条件, 则输出结果, 否则进行软判决; Turbo码分量码生成多项式为[37, 21], 帧长度为1024 bits, 码率为1/3, 伪随机交织, SOVA译码算法, 7 次迭代的方案[13]. 仿真得到的BER性能曲线如图5(HD-BER: 格雷码硬判决译码算法误码率曲线, SD-BER: 格雷码软判决译码算法误码率曲线, UD-BER: 未编码算法误码率曲线, HS-BER: 格雷码自适应译码算法误码率曲线, Turbo-BER: Turbo码译码算法误码率曲线)所示. 其中表1是该数据量的格雷码及Turbo码译码仿真时间表. 为了能更清晰地展示不同编译码方案的效果, 将以图4红框部分为例, 将各方案在接收信噪比为0, 2, 4, 6, 8 dB所得到的图像对应部分展示在图6中.

|
图 5 格雷码及Turbo码译码性能比较 |
| 表 1 格雷码及Turbo码译码仿真时间表(单位: s) |
3.2 性能分析
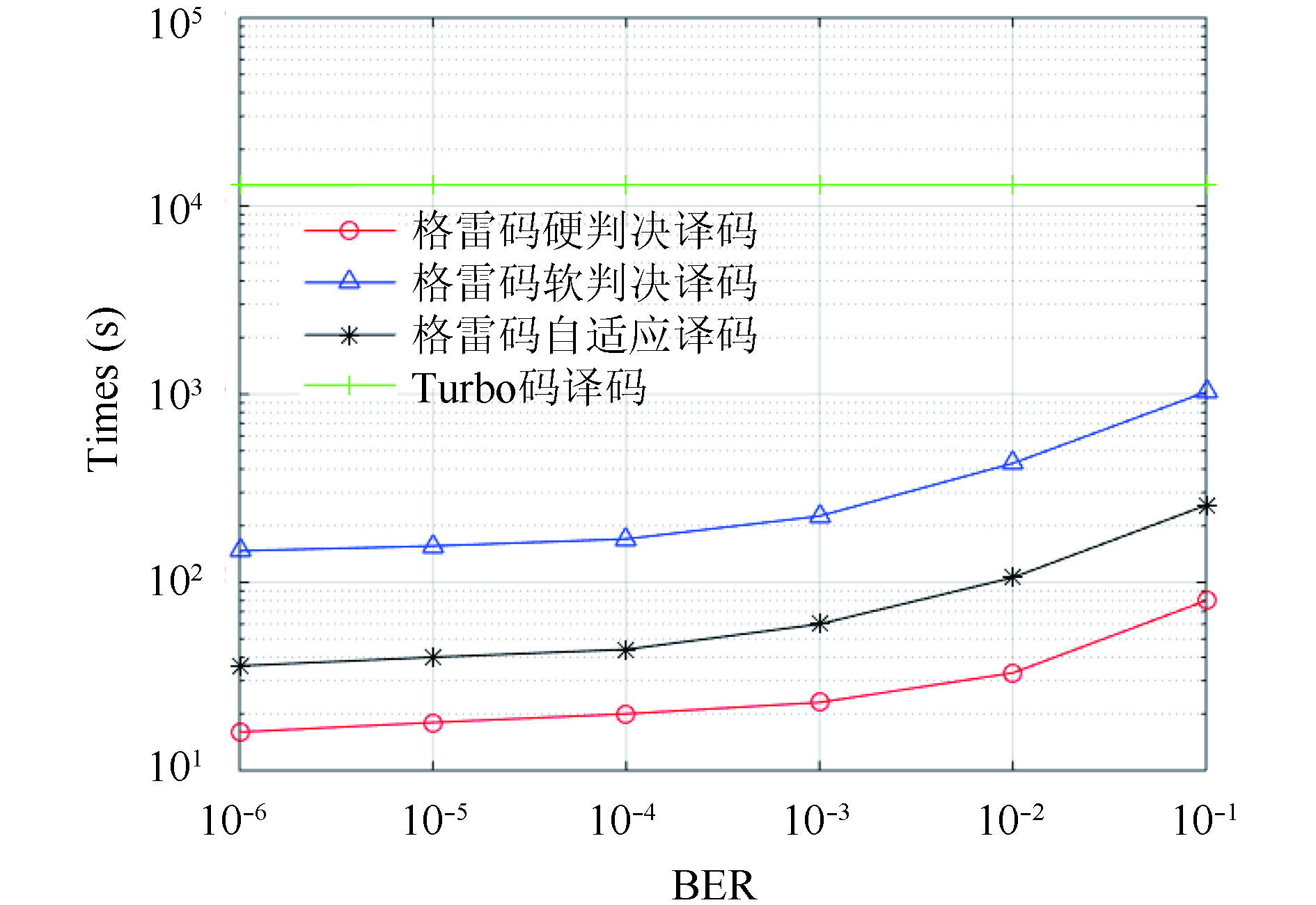
根据图5分析, 当传输并还原后的图片的误码率达到10–6, 也就是达到图片传输的需求后, 格雷码软判决译码机制相对未编码的机制有将近4.2 dB的编码增益, 相对格雷码的硬判决机制有2 dB的编码增益, 本文提出的自适应译码机制达到了同样的效果. Turbo码译码机制相对无编码的机制有将近6.7 dB的编码增益, 相对于格雷码有3 dB的增益. 但Turbo码的优异性能依赖于较长的交织器和进行多次迭代译码, 而使用较长的交织器和进行多次迭代译码, 会延长数据译码的时间, 加大译码器的功耗. 根据表1的数据分析, 格雷码软判决译码算法运行时间大约是硬判决译码算法的7倍, 基于格雷码的自适应译码算法运行时间大约是硬判决译码算法的1.7倍, 大约是软判决译码算法执行时间的25%. 算法执行总时间大约是Turbo码译码算法执行总时间的0.8%. 图7可以很直观的看出在不同的信噪比下格雷码的软硬判决译码速度都比turbo码译码速度要快很多. 从左往右看图7, 误码率BER从10–6到10–4自适应译码算法时间曲线走势更接近格雷码硬判决译码算法时间曲线图, 说明在高信噪比下, 信号出错的几率较小, 格雷码自适应译码算法中硬判决占的比重较大, 同时软判决可以解出硬判决解不了另外的3个及3个以内的比特位错误, 误码率BER从10–3到10–1自适应译码算法时间曲线走势更接近格雷码软判决译码算法时间曲线图, 说明在低信噪比下, 信号出错的几率较大, 格雷码自适应译码算法中软判决占的比重较大, 同时硬判决可以直接解出3个及3个以内的比特位错误. 结合图5 和图7, 我们可以看出本文提出的自适应算法能够在满足图像译码的精度要求的同时, 大大提高了译码的速度. 由图6可以看出随着信噪比的增高, 干扰对信号传输影响逐渐减小. 比较图6可以看出在相同的环境下, 信噪比为2 dB以上的时候, 经过格雷码硬软判决译码传输的图片清晰度明显要高与未编码传输的图片. 经过格雷码软判决及自适应译码的图片清晰度高于格雷码硬判决译码的图片. 信噪比为6 dB时, 经过格雷码软判决及自适应编解码的图片清晰度基本上等同于原图. 结合表1, 我们可以看出自适应译码算法能够配合数据传输的精度的需求, 采用最合适的解码方法以较快的速度达到使用者的精度需求. 经过Turbo码译码的图片在低信噪比情况下的清晰度要高于经过格雷码算法的图片, 但是考虑到我们实际应用的环境的信噪比较高以及Turbo码译码的时间较长, 译码器能耗较高, 选择基于格雷码的自适应译码算法具有显著的优势. 仿真证明该方案是可行的.

|
图 6 不同编译码方式下图像传输效果, 自上而下分别为未编码、Turbo译码、格雷码硬判决译码、格雷码软判决译码、格雷码自适应判决译码图片 |
|
图 7 格雷码硬判决译码、格雷码软判决译码、格雷码自适应判决译码、Turbo译码时间比较图 |
4 结论与展望
本文提出了一种应用于无人机图像传输的基于格雷码的无人机图像传输自适应译码算法. 在高斯信道下, 在格雷码硬判决的基础添加奇偶校验位, 当奇偶校验满足预先设定的校验关系时, 输出译码结果, 否则将数据输入到格雷码的软判决中译码, 可以依据奇偶校验位来权衡译码的精度和速度. 实验表明, 该算法实现成本低, 实现简单, 功耗低, 运算速度快. 因此, 基于格雷码的无人机图像传输自适应译码算法非常适合用于无人机图像传输, 是一种可行的译码算法.
| [1] |
Yoon K, Park D, Yim Y, et al. Security authentication system using encrypted channel on UAV network. Proceedings of the 1st IEEE International Conference on Robotic Computing. Taichung, China. 2017. 393–398.
|
| [2] |
Gao Q, Ji M, Pang L, et al. Design of UAV high resolution image transmission system. International Conference on Optical and Photonics Engineering. Chengdu, China. 2017. 102502Y.
|
| [3] |
Choi M, Lee H, Nam H. Cooperative UAV networks based on distributed space-time block codes. Proceedings of the 13th International Conference on Ubiquitous Robots and Ambient Intelligence. Xi’an, China. 2016. 454–458.
|
| [4] |
Cao HR, Liu YX, Yue XJ, et al. Cloud-assisted UAV data collection for multiple emerging events in distributed WSNs. Sensors, 2017, 17(8): 1818. DOI:10.3390/s17081818 |
| [5] |
Baker CAB, Ramchurn S, Teacy WTL, et al. Planning search and rescue missions for UAV teams. Proceedings of the 22nd European Conference on Artificial Intelligence. The Hague, Holland. 2016. 1777–1782
|
| [6] |
Zhang Y, Su ZB, Shen WZ, et al. Remote monitoring of heading rice growing and nitrogen content based on UAV images. International Journal of Smart Home, 2016, 10(7): 103-114. DOI:10.14257/ijsh |
| [7] |
Messous MA, Senouci SM, Sedjelmaci H. Network connectivity and area coverage for UAV fleet mobility model with energy constraint. Proceedings of 2016 Wireless Communications and Networking Conference. Doha, Qatar. 2016. 1–6.
|
| [8] |
Belov V, Mosin S. FPGA implementation of LTE turbo decoder using MAX-log MAP algorithm. Proceedings of the 6th Mediterranean Conference on Embedded Computing. Bar, Montenegro. 2017. 1–4.
|
| [9] |
许哲, 康永, 黄莺, 等. 无人机测控系统Turbo-MAP译码方法. 火力与指挥控制, 2015, 40(4): 14-17, 22. |
| [10] |
段延森, 王琳, 黎勇. (73,37,13)QR码的一种新型代数硬判决译码算法. 重庆邮电大学学报(自然科学版), 2013, 25(5): 622-627. DOI:10.3979/j.issn.1673-825X.2013.05.011 |
| [11] |
段延森, 王琳. 格雷码的代数软判决译码研究. 重庆邮电大学学报(自然科学版), 2011, 23(5): 565-569. DOI:10.3979/j.issn.1673-825X.2011.05.013 |
| [12] |
余格非, 王振华, 李颖, 等. 信道编码在无人机数据链中的应用研究. 重庆邮电大学学报(自然科学版), 2014, 26(6): 845-849. DOI:10.3979/j.issn.1673-825X.2014.06.019 |
| [13] |
范昭波, 路平. 无人机数据链中Turbo码应用研究. 通信技术, 2008, 41(11): 44-46. DOI:10.3969/j.issn.1672-4844.2008.11.012 |
 2018, Vol. 27
2018, Vol. 27


