2. 上海交通大学附属第六人民医院 神经内科, 上海 201306;
3. 上海交通大学附属第六人民医院 放射科, 上海 201306
2. Department of Neurology, the Sixth People’s Hospital Affiliated to Shanghai Jiaotong University , Shanghai 201306, China;
3. Department of Radiology, the Sixth People’s Hospital Affiliated to Shanghai Jiaotong University, Shanghai 201306, China
最近几年, 由于电子计算机和通信技术的发展, 电子医疗成为一个新型的领域, 得到快速发展, 许多医疗形式逐步出现[1–3], 预测和诊断疾病是一个重要方面. 从医疗检测和可穿戴设备上, 获得健康状态信息, 医师能为病人做出诊断, 或预测病人病情未来发展情况, 帮助病人延缓病情.
偏头痛是一种比较常见的疾病, 会出现经常性的头痛, 同时伴随有畏光、呕吐、恶心等生理反应的慢性神经综合征[4]. 偏头痛发病率较高, 在医学界多年研究中, 也没有找到偏头痛致病机制的有效依据, 对于偏头痛的诊断还缺乏足够的生物学标志[4,5].
静息态功能核磁共振成像技术, 是一种非侵入式探测神经元活动的测量方法, 受到很多学者关注. 静息态功能核磁共振成像, 在分析大脑网络中起着重要的作用[6–8], 已经应用在分析各种精神疾病上[9], 比如: 老年痴呆[10]、帕金森[11]和精神分裂症[12].
近年来, 由于深度学习在语音识别和图像处理中, 取得突破性的进展, 被广泛应用在各种工程领域. 最近, 国内外很多学者将深度学习用于功能核磁共振成像数据分析, 诊断阿尔茨海默症, 得到相对理想的预测效果. 在用深度学习诊断阿尔茨海默症中, 更多论文采用softmax分类器与深度模型一起训练. 此类算法根据softmax分类器分类正确率为依据, 调整深度模型各个隐藏层神经单元的权重, 使得分类正确率达到一个理想的结果之后停止迭代. 此类算法与传统的浅层分类器相比, 分类正确率更高[13,14]. 由于此类算法在提取数据特征时, 用到大量的先验信息, 即已经拥有大量的确诊病例, 可以在实验样本数相对丰富的条件下, 训练网络达到理想效果. 由于阿尔茨海默症临床症状表现明显, 在确诊上相对容易, 获得较多的实验样本并不困难. 而偏头痛在临床诊断上相对复杂, 病例确诊相对困难, 较难获取大量实验样本数据. 采用softmax分类器与深度模型一起训练的算法, 因为实验样本较少效果并不理想. 本文采用深度学习的深度自编码器算法, 该算法根据输入样本数据和输出样本数据的差异, 更新各隐藏层神经元权重, 因此在提取实验样本数据特征时, 不需要知道实验样本数据是健康被试或偏头痛患者. 该算法不需要过多确诊病例样本来训练神经网络, 提取有效特征. 这符合人们在对偏头痛的致病机理尚不明确的前提下, 有效检测偏头痛. 本文最后实验结果说明, 深度自编码器获取的数据特征, 应用到各种分类算法中都能提高分类正确率.
1 数据的采集与预处理本文偏头痛数据为上海交通大学附属第六人民医院(东院)经过临床确诊的24例数据, 去除不合格的数据后还剩17例, 平均年龄为45.6岁. 同期选取了100个正常人作为健康对照组, 平均年龄43.5岁. 该fMRI数据采用Siemens MRI仪(3T)数据获取时, 要求被试者保持大脑清醒, 并平躺于MRI仪器内, 不做任何思考. 扫描参数: 采用单次激发敏感梯度回波平面成像, 切片数为38, 覆盖整个脑区, TR 3.0 s, 扫描分辨率为64×64, 片内分辨率为4 mm×4 mm, 片厚度4 mm.
采用SPM8[15] 对静息态功能磁共振数据进行预处理, 主要进行时间层矫正、头动矫正、图像标准化等步骤. 在头动矫正过程中, 配准时在任何方向上位移>1.5 mm或头部转动>1.5°的数据均被丢弃; 带通滤波器参数为0.01 Hz<f<0.1 Hz, 以降低低频漂移及高频的生物噪音.
自动解剖标签模板[16]将小脑去除在外, 大脑被分为90个脑区. 通过计算每个脑区之间的皮尔森相关系数, 可以获得一个90×90的对称矩阵. 然后获取该对称矩阵的上三角部分, 并且将其所有元素放在一行, 作为一个被试样本的特征数据.
2 深度学习模型 2.1 自动编码器自动编码器可以自动获取待分析数据的特征, 而不需要专家通过先验知识提取特征. 经典自动编码器有一个输入层、一个隐藏层和一个输出层. 输入层和输出层的神经元个数相等. 自动编码器是无监督学习方法, 复杂的高维数据被自动编码为低维数据. 自动编码器尝试逼近一个恒等函数, 从而使得输出值
具体说, 编码函数映射向量
| ${h} = {\partial _1}({{w}_1}{x} + {{b}_1})$ | (1) |
| $\hat{ x} = {\partial _2}({{w}_2}{x} + {{b}_2})$ | (2) |
自动编码器的参数
| ${L_H}\left( {{x},\hat{ x}} \right) = - \sum\limits_{i = 1}^d {{{x}_{{i}}}\log {{\hat{ x}}_{{i}}}} + (1 - {{x}_{{i}}})\log (1 - {\hat{ x}_{{i}}})$ | (3) |
这是一个最基本的自动编码器的构成, 下面将介绍如何将它们组合在一起构造出深度模型.
2.2 构造深度自动编码器如图1所示构造具有3个隐藏层的自动编码器. 可以看出, 第一个隐藏层神经元个数少于输出层神经元个数. 第二个隐藏层神经元个数少于第一个隐藏层神经元个数, 以此类推, 每一个隐藏层神经元个数都少于前面隐藏层神经元个数, 最后输出层神经元个数扩大到与输入层神经元个数相同. 加入输出层是为了损失函数可以估算, 最后输出数据与输入数据的区别, 从而可以根据区别程度, 更新自动编码器的权重. 自动编码器自动提取的突显特征在最后一个隐藏层, 用第三个隐藏层输出的数据, 作为自动编码器自动获得的特征. 通过逐渐减少隐藏层神经元个数, 迫使自动编码器学习输入数据低维表示. 这种结构能捕获到输入数据特征在特定空间上的分布, 并且将高维的复杂数据降低到低维数据. 用Adadelta优化算法训练整个网络, 它能根据学习环境自动调节学习参数. 激活函数采用非线性函数Relu, 通过采用非线性激活函数, 自动编码器能学习到, 不同于采用主成分分析得到的数据特征. 自动编码器获得的特征, 可以用带有少量参数的非线性函数表示更复杂的函数. 因此, 深度模型完全不同于浅层模型[17]

|
图 1 构造拥有三个隐藏层的深度自动编码器 |
深度自动编码器中, 输入层、输出层、各个隐藏层神经元个数和激活函数如表1所示, 此模型迭代训练7000次之后, 作为训练完成的深度自动编码器.
3 实验步骤与结果 3.1 实验过程与步骤本文用两种方法训练分类器, 其一, 如图2(a)所示, 用自动解剖标签模板获得fMRI样本特征, 训练传统分类器, 测试分类正确率. 其二, 如图2(b)所示, 用模板获得的特征训练自动编码器, 已训练的自动编码器提取精细特征之后, 训练传统分类器.
| 表 1 深度自动编码器各层神经元个数和激活函数 |

|
图 2 分类器训练方法 |
根据自动解剖模板获取的特征, 作为原始特征, 自动编码器自动获得的特征, 作为精细特征, 分别用这两种特征, 比较各种分类算法达到的正确率. 分别用线性支持向量机(线性-SVM)、k近邻、径向基核函数支持向量机(RBF-SVM)和决策树进行分类. 分类算法各参数配置为scikit-learn软件包中, 各种算法的默认配置. 首先, 选10个偏头痛原始特征和10个健康人原始特征, 作为训练数据, 训练以上4种分类器和深度自动编码器. 将剩下的7个偏头痛数据, 加上另外随机选取的7个健康对照组数据, 作为测试数据, 验证各种分类器分类正确率. 发现7个偏头痛数据, 不管是在原始特征作为分类器的输入数据下, 还是在精细特征作为分类器的输入数据下, 7个偏头痛数据都能进行正确分类. 而7个健康人数据, 在原始特征作为分类器的输入数据下, 出现个别错误.
由于偏头痛数据采集困难, 数据样本不多, 而仅有的7个测试数据都被各个分类器正确分类, 无法在大样本下, 检验各个分类器将偏头痛分进健康对照组的错误率. 健康对照组样本数量相对较多, 可以在健康对照组中, 检验各个分类器将健康人分进偏头痛的错误率. 将其余83个健康人数据, 作为测试数据, 检验各个分类器的分类性能.
3.2 实验结果| 表 2 原始特征训练的分类器分类正确率和分类错误个数 |
| 表 3 精细特征训练的分类器分类正确率和分类错误个数 |
|
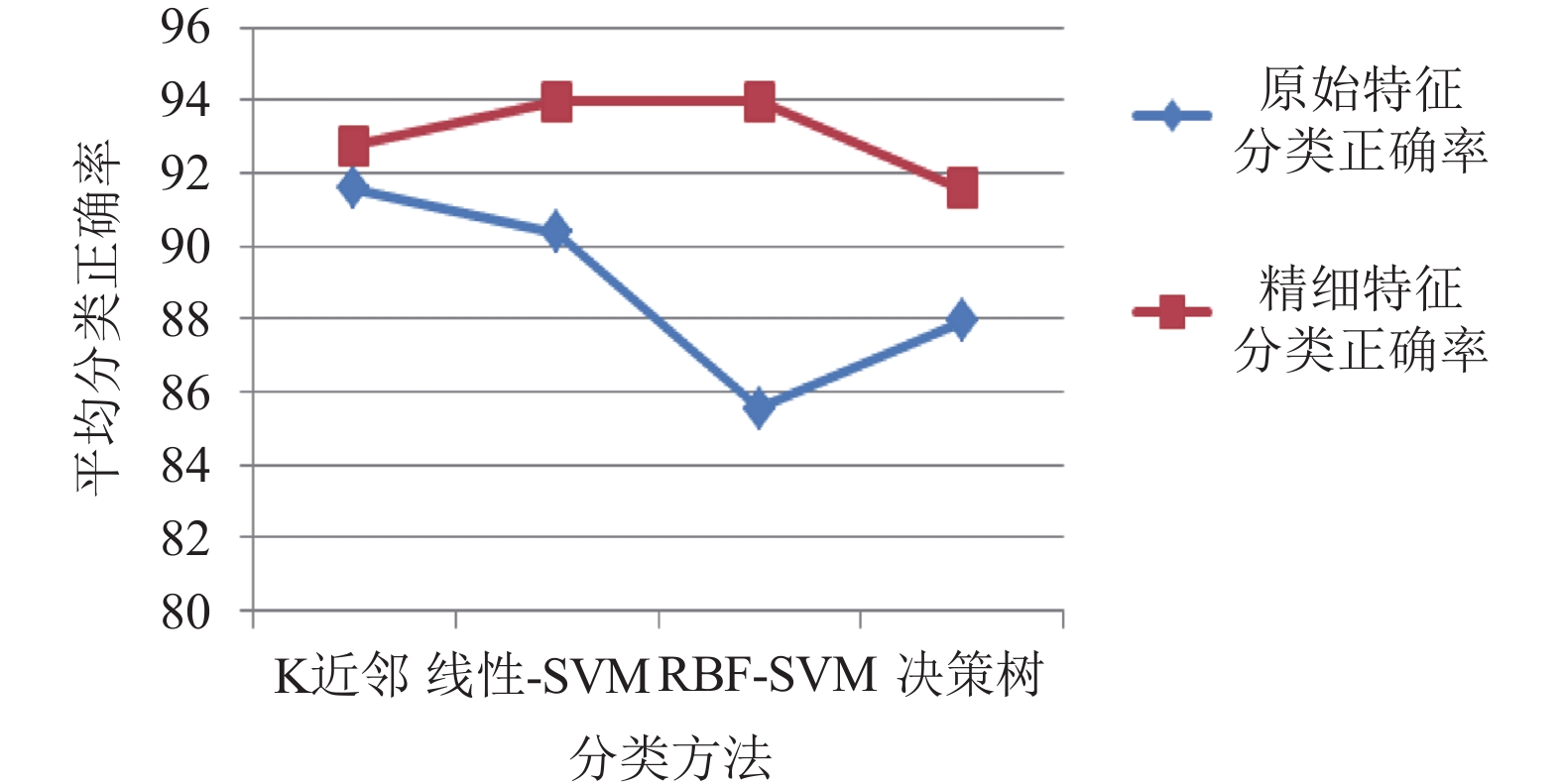
图 3 各种分类器, 分类健康对照组的正确率 |
4 讨论
如表2所示, 用83个健康人数据, 在原始特征下训练的分类器, 分类健康人的实验结果. RBF-SVM在原始特征作为训练数据下, 分类效果最差, 决策树效果次之. 线性-SVM分类效果好于RBF-SVM, 可能由于原始特征在原始维度空间中, 数据分布已经较好的达到线性可分程度. 用RBF-SVM将数据映射到更高维的空间中, 寻找分类超平面, 分类效果反而没有线性-SVM分类效果好, 说明在原始空间中的数据映射到高维空间中, 支持向量机没有找到很好的分类超平面分类数据.
如表3所示, 经过深度学习提取特征之后, RBF-SVM分类效果和线性-SVM分类效果都有所提高, 并且高于其他分类器分类效果. RBF-SVM将精细特征映射到高维空间后, 能找到更好的分类超平面分类数据. 说明, 深度学习提取的特征分布, 更适合映射到高维空间, 寻找到更好的分类超平面.
如图3所示, 分别用精细特征和原始特征训练各个分类器, 得到的分类正确率. 从图中可以看出, 经过深度学习提取的精细特征, 在分类正确率上, 明显高于用原始特征训练的各个分类器. 可以说明, 深度学习提取的特征, 可以提高一些分类器分类效果, 在预测偏头痛上, 拥有更高预测效果.
自动解剖标签模板提取的原始特征, 训练分类器, 各个分类器的平均分类正确率, 能达到88.86%. 说明, 偏头痛病人存在特殊的脑功能网络, 这个脑功能网络与正常人的脑功能网络, 存在一定差异, 使得用传统分类器也能达到较高的分类正确率. 但是, 因为拥有多层结构来提取特征, 深度学习拥有更完美的方式表达特征. 在我们构建的自动编码器中, 输入的大脑区域相关性, 被表达为更高层次的描述. 各个分类器的平均分类正确率, 达到93.07%就是最好的证明.
在深度学习中, 输入数据经过已经训练好的自动编码器, 提取出拥有更好分类界限的特征, 为传统分类器提高分类效果. 在自动编码器每个隐藏层中, 每个神经元的权重, 能表达新的物理学和生理学意义. 通过分类挑选和校验大量的权重, 能找到某2个脑区的相关系数, 对于预测偏头痛起到更重要的作用.
5 结论与展望偏头痛在临床诊断中没有影像学诊断标准, 通过我们对偏头痛患者静息态功能磁共振的研究, 提出一种深度学习的特征提取方法, 在不需要较多先验知识的前提下, 提取出精细特征, 提高各种分类器分类效果. 经过深度学习提取的特征, 在各种分类器分类结果中, 都能有效提高分类正确率. 进一步研究, 可以获得更多的偏头痛数据, 用更多的样本数据训练分类器, 从而提高分类器分类效果, 为临床诊断偏头痛提供重要的影像参考.
| [1] |
Sloot PMA, Tirado-Ramos A, Altintas I, et al. From molecule to man: Decision support in individualized e-health. Computer, 2006, 39(11): 40-46. DOI:10.1109/MC.2006.380 |
| [2] |
Ronga LS, Jayousi S, Del Re E, et al. TESHEALTH: An integrated satellite/terrestrial system for e-health services. Proceedings of 2012 IEEE International Conference on Communications (ICC). Ottawa, ON, Canada. 2012. 3286–2890.
|
| [3] |
Liang J, Sahama T. Online multiple profile manager for eHealth information sharing. Proceedings of 2012 IEEE International Conference on Communications (ICC). Ottawa, ON, Canada. 2012. 3461–3465.
|
| [4] |
Kim JH, Suh SL, Seol HY, et al. Regional grey matter changes in patients with migraine: A voxel-based morphometry study. Cephalalgia An International Journal of Headache, 2008, 28(6): 598-604. DOI:10.1111/j.1468-2982.2008.01550.x |
| [5] |
Cutrer FM, Black DF. Imaging findings of migraine. Headache: The Journal of Head and Face Pain, 2006, 46(7): 1095-1107. DOI:10.1111/hed.2006.46.issue-7 |
| [6] |
Schwedt TJ, Dodick DW. Advanced neuroimaging of migraine. The Lancet Neurology, 2009, 8(6): 560-568. DOI:10.1016/S1474-4422(09)70107-3 |
| [7] |
Shi YH, Zeng WM, Wang NZ, et al. A novel fMRI group data analysis method based on data-driven reference extracting from group subjects. Computer Methods and Programs in Biomedicine, 2015, 122(3): 362-371. DOI:10.1016/j.cmpb.2015.09.002 |
| [8] |
Shi YH, Zeng WM, Wang NZ. SCGICAR: Spatial concatenation based group ICA with reference for fMRI data analysis. Computer Methods and Programs in Biomedicine, 2017, 148: 137-151. DOI:10.1016/j.cmpb.2017.07.001 |
| [9] |
Shi YH, Zeng WM, Wang NZ, et al. A new method for independent component analysis with priori information based on multi-objective optimization. Journal of Neuroscience Methods, 2017, 283: 72-82. DOI:10.1016/j.jneumeth.2017.03.018 |
| [10] |
Ferri R, Rundo F, Bruni O, et al. Small-world network organization of functional connectivity of EEG slow-wave activity during sleep. Clinical Neurophysiology, 2007, 118(2): 449-456. DOI:10.1016/j.clinph.2006.10.021 |
| [11] |
Guo ZW, Liu XZ, Jia XZ, et al. Regional coherence changes in alzheimer’s disease patients with depressive symptoms: A resting-state functional MRI study. Journal of Alzheimer’s Disease, 2015, 48(3): 603-611. DOI:10.3233/JAD-150460 |
| [12] |
Wu T, Long XY, Zang YF, et al. Regional homogeneity changes in patients with Parkinson’s disease. Human Brain Mapping, 2009, 30(5): 1502-1510. DOI:10.1002/hbm.v30:5 |
| [13] |
Liu SQ, Liu SD, Cai WD, et al. Early diagnosis of Alzheimer’s disease with deep learning. Proceedings of the 11th International Symposium on Biomedical Imaging (ISBI). Beijing, China. 2014. 1015–1018.
|
| [14] |
Suk HI, Shen D. Deep learning-based feature representation for AD/MCI classification. In: Mori K, Sakuma I, Sato Y, et al. eds. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2013. Berlin, Heidelberg: Springer, 2013. 583–590.
|
| [15] |
SPM. http://www.fil.ion.ucl.ac.uk/spm. [2018-01-03].
|
| [16] |
Tzourio-Mazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage, 2002, 15(1): 273-289. DOI:10.1006/nimg.2001.0978 |
| [17] |
Bengio Y, Lecun Y. Scaling learning algorithms towards AI. In: Bottou L, Chapelle O, DeCoste D, et al. eds. Large-Scale Kernel Machines. Cambridge, MA. MIT Press, 2007. 321–359.
|
 2018, Vol. 27
2018, Vol. 27



