2. 福建师范大学 数学与信息学院, 福州 350108
2. College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350108, China
序列数据挖掘是数据挖掘领域中的一个研究热点, 序列数据广泛存在于各个领域[1–3], 如交通路网中的出租车出行轨迹序列、用户的网上购物行为序列、生物DNA序列等, 如何精确且高效地建模和挖掘序列数据蕴含的模式特征, 具有重要意义. 马尔科夫模型是一种经典的概率统计模型, 具有良好的统计特征和状态的无后向性等优点, 常用来对序列数据建模, 进行位置预测、用户推荐、DNA分类等研究, 该模型在实际应用中[4,5], 注重解决两个问题: 一是模型的阶长问题, 二是模型实现的时间和空间效率问题. 针对第一个问题, 传统的固定阶模型, 低阶模型由于未能充分使用更多的历史状态信息, 存在精度不高问题, 高阶模型随着阶数的增长, 状态空间复杂度呈指数级增长, 存在空间膨胀问题, 同时阶数过高, 历史样本数据覆盖率低. 高阶模型存在样本数据覆盖率不足问题. 为了兼顾建模的精度和复杂度, 学者们引入变阶的思想, 提出了变阶马尔科夫模型[6], 能建立任意阶长的马尔科夫链模型, 根据实际情况动态自适应使用合适的阶长进行计算, 模型自提出后得到广泛的研究[7,8]与应用[9–11]. 对于第二个问题, 模型实现的效率问题, 当前的各类研究与应用中, 一类研究侧重模型的建模细节本身, 未涉及具体的模型实现, 如文献[12]使用变阶马尔科夫模型预测移动位置, 其实质是一种历史模式匹配的方法, 根据最大匹配的阶长来使用, 不能实现真正意义上的变阶切换计算; 另一类研究针对具体应用情况给出实现方法, 如文献[13,14]给出了一种概率后缀树的实现算法, 解决生物序列分类问题, 但其实现复杂度较高, 且算法需要预设模型的阶长; 还有一类研究从纯算法实现的角度, 引入概率后缀树数据结构快速构造模型[15]. 针对概率后缀树实现算法时空复杂度高的问题, 文献[15]从理论上证明了在线性时间与空间复杂度内构建概率后缀树的可行性, 可在线性时间内构造一个等价的自动机, 而文献[16]从概率后缀数组的角度提出了变阶马尔可夫模型的一种等价概率后缀树的线性实现.
本文针对变阶马尔科夫模型的树结构实现过程中存在的复杂度高问题, 从后缀结构的角度, 提出了基于后缀数组和后缀自动机的变阶马尔科夫模型实现算法, 算法借助于后缀链能在线性时间和空间复杂度内构建模型, 通过对比实验表明, 算法具有较好的效率, 能够实现在线建模学习和应用.
1 变阶马尔科夫模型马尔科夫模型(Markov Model, MM)是一个经典的概率模型, 假设S是一个由有限个状态序列组成的集合. 令S={Xi, i=1, 2, 3}, 则有:
| $\begin{array}{l}P(X_{n + 1} = j|X_n = i_n,X_{n - 1} = i_{n - 1},\cdots,X_1 = i_1)\\ = P(X_{n + 1} = j|X_n = i_n,X_{n - 1} = i_{n - 1},\cdots,X_{n - L + 1} = i_{n - L + 1})\end{array}$ | (1) |
该马尔科夫模型称为L阶马尔科夫模型. 当前状态序列的概率由过去的L个已知状态序列的概率决定, L=1时为标准马尔科夫模型.
有限状态序列
| $\begin{align}P(X_{n - l + 1},\cdots,X_n) = & P(X_{n - l + 1}) P(X_{n - l + 2}|X_{n - l + 1})\cdots\;\\ & P(X_n|X_{n - l + 1},\cdots,X_{n - 1})\end{align}$ | (2) |
其中, 算式右边的每项累乘项, 概率P的计算均对应某阶长的马尔科夫过程, 如
因此, 变阶马尔科夫模型需要索引各子序列的概率分布及其后缀序列之间的转移跳转关系, 从而快速实现变阶长度的子序列概率计算.
2 变阶马尔科夫模型的实现变阶马尔科夫模型拥有后缀特性, 此特性使得可以用树结构来表示模型, 在后缀结构当中, 每个节点都表示一个对应的后缀串, 后缀链指向的是最长能匹配的并且以相同后缀结尾的后缀子串的位置. 使用变阶马尔科夫模型计算序列概率时, 在利用后缀数据结构构造好的字符串上查找失配时, 只需要通过后缀链跳转到对应位置, 实现快速降阶计算.
本文主要提出了3种表达后缀结构的模型及算法原理与实现.
2.1 基于字典树的变阶马尔科夫模型字典树(Trie Tree, TT)又称单词查找树, 能充分利用字符串的公共前缀减少查询时间, 减少字符串比较, 其特征为: 除根节点为空字符, 其它节点都表示一个字符, 从根节点遍历到树上某一节点, 路径所对应的字符串, 即为该节点所表示的字符串.
模型构建过程包括两部分: 1)构建后缀字典树, 2)添加后缀链.
2.1.1 构建后缀字典树对于长度为N的字符串S, 共有N个后缀串, 定义Suffix(i)表示以i为开头的后缀串, 新建一棵字典树, 字典树的每个节点要统计这个节点所表示的字符串出现次数, 因此每个节点存放一个cnt用来计数. 将Suffix(1),…,Suffix(N)这N个后缀串插入到字典树中, 插入每个后缀串的同时, 将这个后缀串所经过的节点的cnt值加1, 全部后缀串插入完毕即得到一棵索引了样本所有后缀串的字典树. 以cactt的所有后缀串为例构造字典树, 将cactt的5个后缀串全部插入, 并同时计算每个节点的cnt值(节点下标按照插入顺序), 如图1所示.

|
图 1 cactt后缀字典树 |
效率分析: 长度为N的字符串, 共有N个后缀串, 长度分别为1, 2, …, N, 所有后缀串的字符总个数为N(N+1)/2, 字典树对于每次插入后缀串, 最坏情况下需要新建该后缀串长度个数的节点, 因此时间和空间复杂度均为O(N2), 算法伪代码如算法1.
算法1. BuildTrie (创建后缀字典树)
输入: 训练序列x, 序列长度len
输出: 后缀字典树Trie
(1) Trie ← TrieInit()
(2) for i← 0 to len-1 do
(3) InsertToTrie(x[i,…, len–1], Trie)
(4) end for
(5) return Trie
子算法 InsertToTrie
输入: 后缀树Trie, 训练序列x, 插入序列开始位置l, 结束位置r
输出: 后缀字典树Trie
(1) u ← 1
(2) node ← Trie.node
(3) node[u].cnt ← node[u].cnt +1
(4) for i ←ltor do
(5) c ← x[i]
(6) if node[u].to[c] ==0 then
(7) Trie.sz← Trie.sz +1
(8) node[sz]← Node()
(9) node[u].to[c]← sz
(10) end if
(11) u ← node[u].to[c]
(12) node[u].cnt ← node[u].cnt +1
(13) end for
(14) return Trie
2.1.2 添加后缀链为了实现后缀序列之间的快速跳转, 需要建立链接关系, 算法思想为: 每个节点定义一个指针slink, 指向后缀链跳转的节点, 利用一个队列进行层次遍历, 遍历的过程不断计算后缀链, 通过这种顺序, 当需要计算一个节点的后缀链时, 其父亲节点的后缀链信息将已经被计算出来, 而当前节点表示的后缀串, 前缀必然是包含了他父亲节点所表示的后缀串的, 且当前节点表示的后缀串去掉第一个字符所表示的后缀串, 必然也是存在的, 那么可以利用父亲节点的后缀链信息进行跳转, 跳转之后进入该字符的下一个节点, 则该节点即为当前节点后缀链所要指向的节点. cactt后缀字典树添加后缀链后如图2所示.
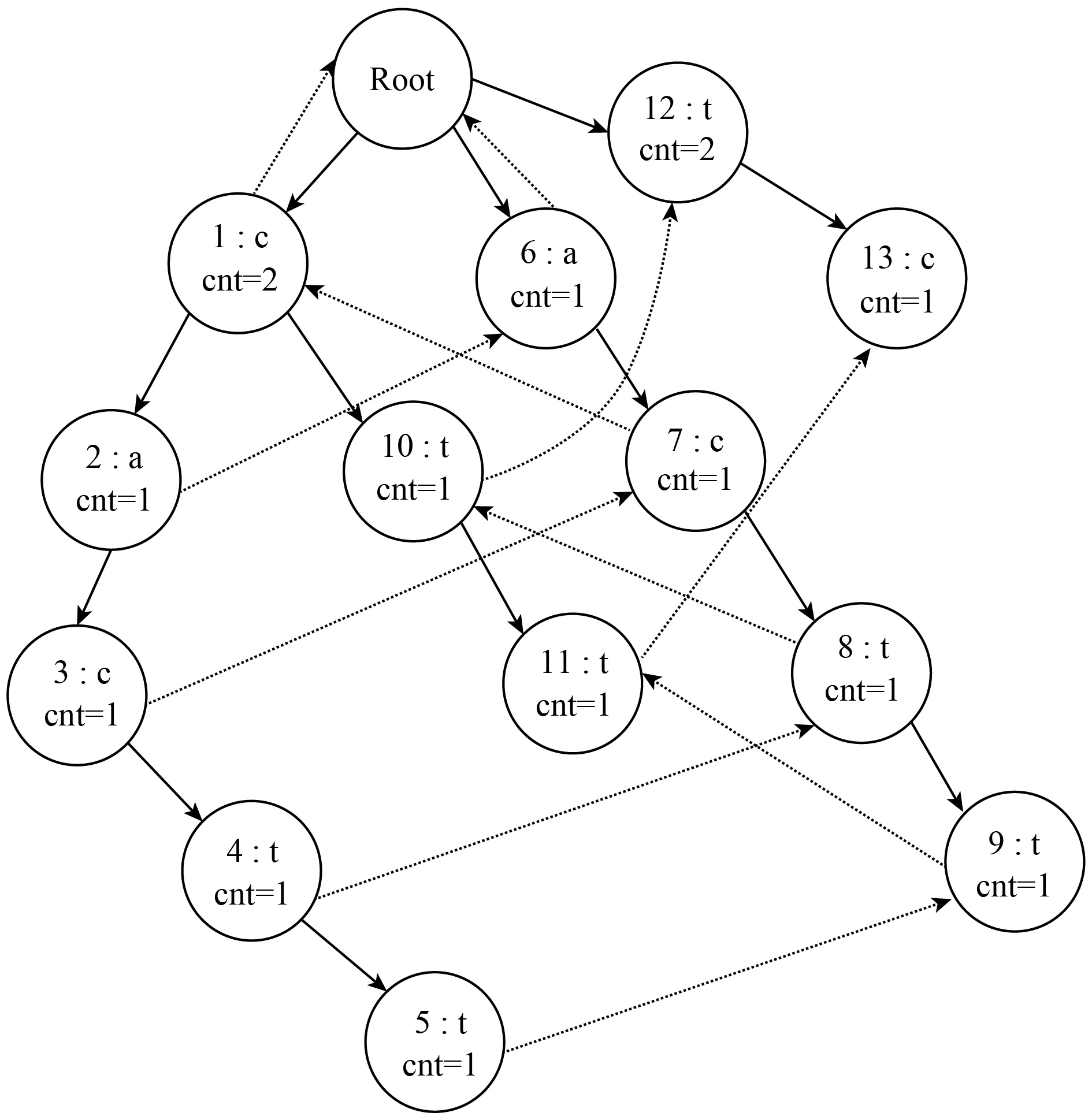
|
图 2 cactt的后缀字典树(虚线为后缀链) |
算法2. BuildSlink (添加后缀链)
输入: 训练序列x, 序列长度len, 后缀字典树Trie, 字符集大小sigma_sz
输出: 添加后缀链的后缀字典树Trie
(1) node ← Trie.node
(2) Q ← new Queue
(3) for i ← 1 to sigma_sz do
(4) v ← node[1].to[i]
(5) if v==0 then
(6) continue
(7) end if
(8) Q.push(v)
(9) node[v].slink ← 1
(10) end for
(11) while Q.size() >0 do
(12) u ← Q.front()
(13) Q.pop
(14) for i ← 1 to sigma_sz do
(15) v← node[u].to[i]
(16) if v ==0 then
(17) continue
(18) end if
(19) node[v].slink← node[node[u].slink].to[i]
(20) Q.push(v)
(21) end for
(22) end while
(23) return Trie
在算法2中, 代码第3–10行单独处理根节点的儿子节点的后缀链信息, 做法与第14–20行代码基本一致.
2.2 基于后缀数组的变阶马尔可夫模型后缀数组(Suffix Array, SA)是后缀树的一个等价模型, 在空间开销上优于后缀树, 常运用于词频统计与处理字符串的后缀信息.
模型构建过程包括两部分: 1)利用后缀数组构造后缀树, 2)添加后缀链.
2.2.1 后缀数组构造后缀树算法思想: 对于一个长度为N的字符串S, 先用构造后缀数组的DC3算法, 线性构造出该字符串的后缀数组Sa, 后缀最长公共前缀数组Lcp, 利用队列扩展后缀树, 首先放入根节点, 表示排名[1, N]的后缀串, 长度为0. 每次从队列取出一个节点, 该节点表示排名[l, r]的相同后缀串, 长度为len, 此节点能表示该后缀串的个数为(r–l+1). 之后将区间划分为[l, r1], [r1, r2],…, [rx, r], 每个区间具有leni长度的公共前缀, 将具有相同公共前缀的区间进行合并, 并将这些区间新建一个节点, 放入队列中继续拓展, 这样每个节点的后继节点个数就是划分出的区间个数, 并且个数是不大于字符集的. 以字符串cactt为例, 如图3所示.

|
图 3 cactt的后缀树结构 |
1) 利用DC3算法构造后缀数组, 得到cactt的后缀数组信息, 如表1所示.
| 表 1 cactt后缀数组信息 |
2) 利用后缀数组统计得到各个排名后缀串与前一排名后缀串的最长公共前缀Lcp, 如表2所示.
| 表 2 cactt最长公共前缀数组信息 |
3) 每个节点表示的信息为(l, r,len), 其中第一个节点Root(0, 4, 0), 加入队列处理后可拓展出3个节点信息, 并将新的节点信息加入到队列之中, 节点信息如表3所示.
| 表 3 结点及后缀信息 |
4) 重复步骤3), 直到队列中的不存在任何节点, 可得最终的后缀树如图4所示.
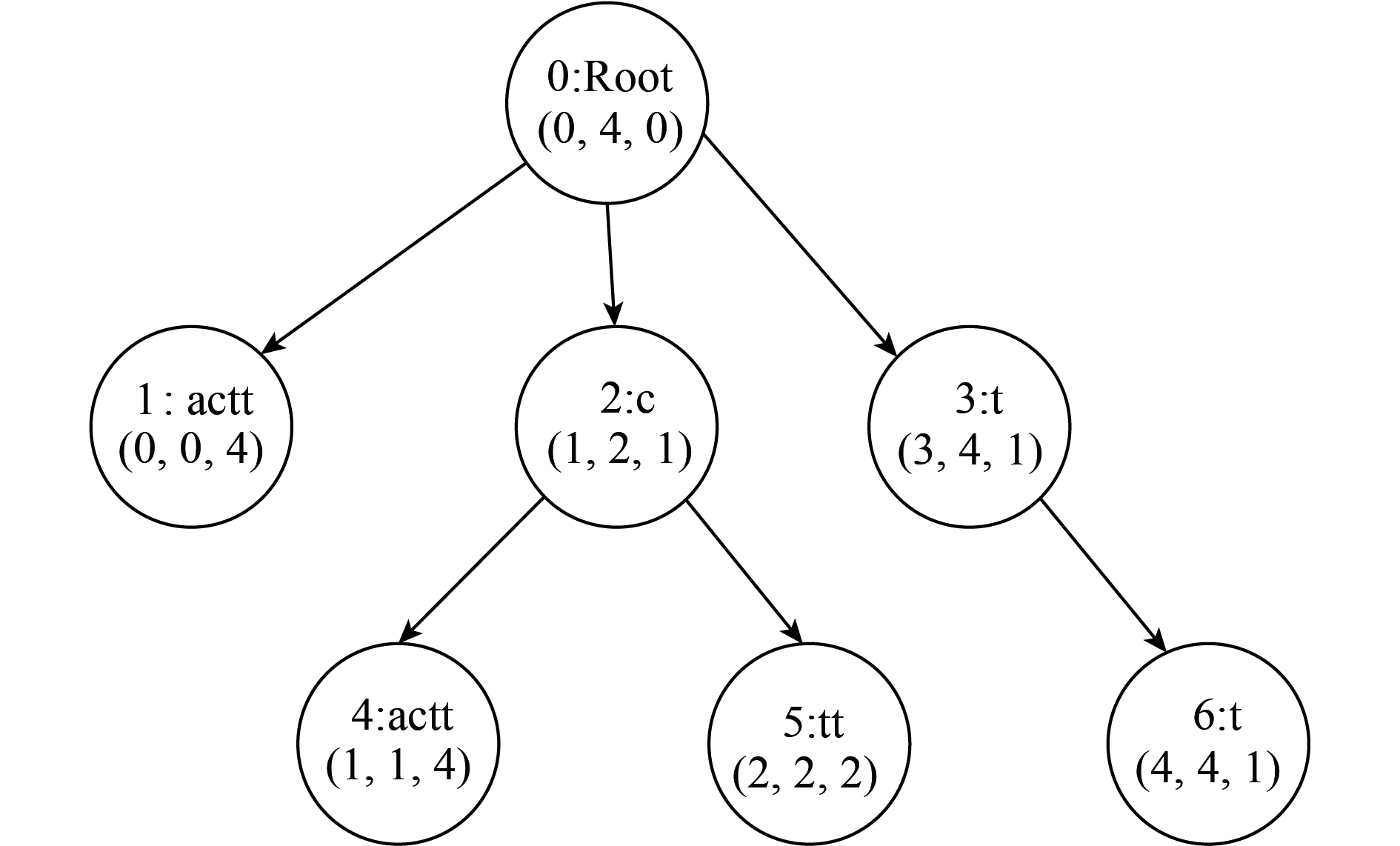
|
图 4 cactt的后缀树 |
效率分析: 定义字符集大小为|C|, 构造出的后缀树的节点个数是O(N)级别, 队列的每次扩展对于一个节点只会入队出队一次, 每次扩展到后继节点, 需要做|C|次二分查找, 每次效率为log(N), 由于字符串的字符集较小, 近似于常数, 因此总体时间复杂度为O(Nlog(N)), 空间复杂度为O(N). 实际上, 二分查找过程, 可以采用线性枚举, 理论上最坏的时间复杂度退化到O(N2), 实际上除了一些特殊序列(例如整个序列都是同一个字符)会达到这个最差复杂度, 大部分随机序列的构造效率趋近于线性O(N).
算法3. BuildSa (创建后缀树)
输入: 训练序列x, 序列长度len
输出: 后缀树的根节点指针root
(1) Sa ← BuildSa(x)
(2) Lcps ← GetLcp(x, Sa)
(3) Q ← new Queue
(4) root ← Node(0, len–1, 0)
(5) Q.push(root )
(6) while !Q.isEmpty do
(7) u ← Q.front()
(8) Q.pop()
(9) if u.l == u.r then
(10) continue
(11) end if
(12) pre ← u.l
(13) while pre <= u.r do
(14) v ← BinarySearch(pre)
(15) Q.push(Node(pre, v, GetLCP(pre, v)))
(16) pre = v
(17) end while
(18) end while
(19) return root
代码1, 2行, 通过DC3算法构造后缀数组, 再统计出最长公共前缀; 第3–5行, 建队列并初始化root节点信息加入队列; 第13–15行, 查找具有公共前缀的最大区间范围[pre,v], 并计算出公共前缀长度, 新建节点信息加入至队列当中.
2.2.2 后缀数组添加后缀链每个后缀链为一个二元组信息(to, len)表示在当前节点失配len长度时, 跳转到to指针指向的节点位置. 其构造思想为: 利用队列层次遍历构造完成的后缀树, 队列中存放元素为指向节点的指针u, 访问节点u时, 判断节点u的所有字符是否均已匹配完毕, 如果匹配完毕, 则匹配下一个节点, 否则, 在当前节点继续匹配. 遍历过程中每次利用父节点或者同一个节点上一个字符的位置, 所保存的后缀链信息, 去构造出当前位置的后缀链信息.
通过上述过程, 可得cactt后缀树每个节点的后缀链信息为表4, 加入后缀链的cactt后缀树结构可见图5.
| 表 4 cactt后缀链信息 |
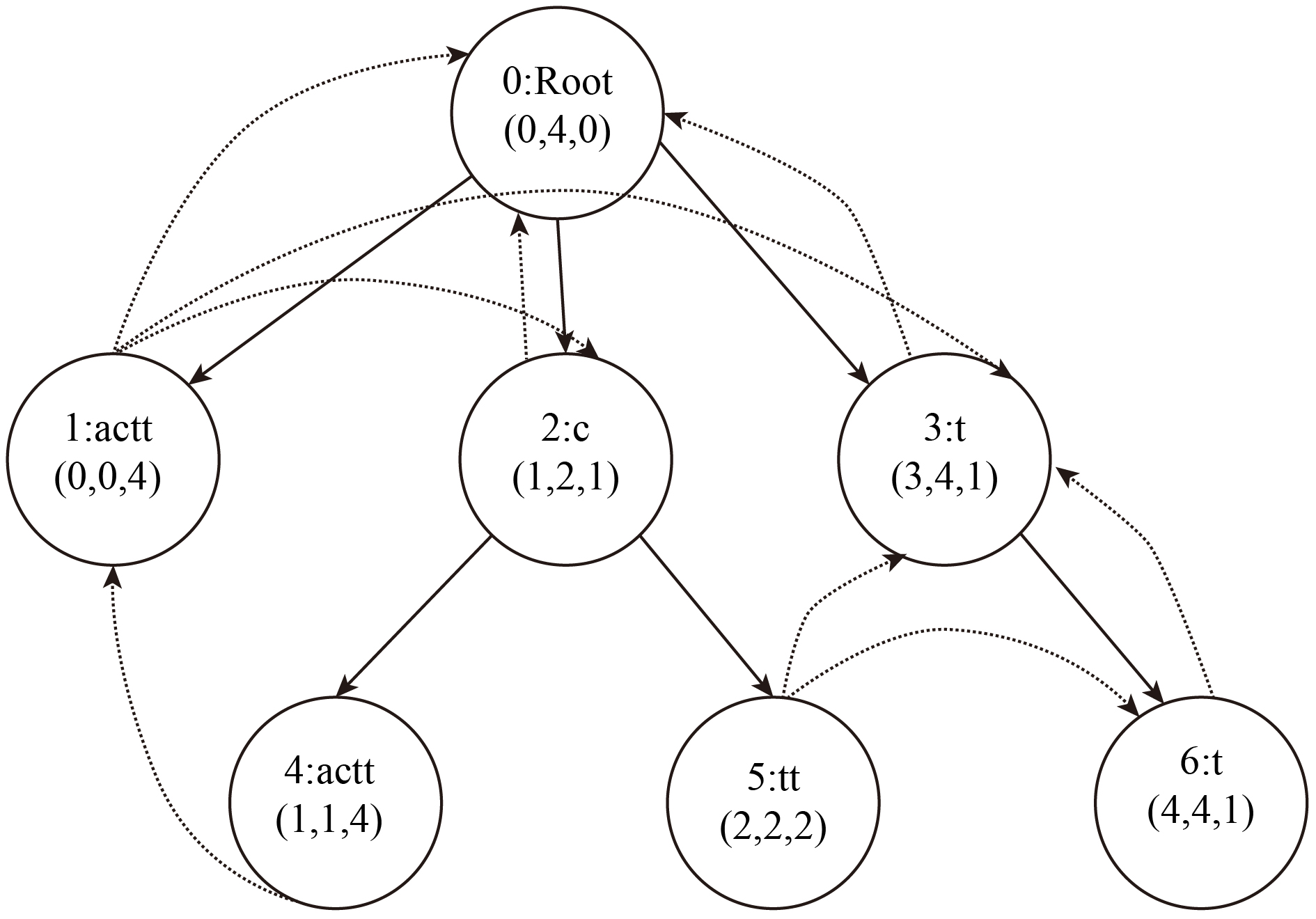
|
图 5 cactt带后缀链的后缀树(虚线为后缀链) |
算法4. BuildSLink (添加后缀链)
输入: 后缀树节点数组node, 训练序列x, 序列长度len, 字符集大小sigma_sz
输出: 已添加后缀链的后缀树节点数组node
(1) Q ← new Queue
(2) Q.push(0)
(3) node[0].slinks.push( Slink(–1, 0))
(4) initSlinksToRootChild(0, node, Q)
(5) while Q.size > 0 do
(6) u ← Q.front()
(7) Q.pop()
(8) fori ← 1 to sigma_sz do
(9) v ← node[u].to[i]
(10) if v == 0 then continue
(11) end if
(12) slink ← node[node[u].slinks.last.to].to[i]
(13) node[v].slinks.push(Slink(slink, 1))
(14) len ← getlen(v)
(15) cmpLen← getlen(slink)
(16) while cmpLen < len do
(17) ch ← getCharIndex(x, v, cmpLen)
(18) slink← node[slink].to[ch]
(19) node[v].slinks.push(Slink(slink, cmpLen+1))
(20) cmpLen ← cmpLen + getlen(slink)
(21) end while
(22) end for
(23) end while
(24) return node
在算法4中, 第3行, 给根节点Root添加后缀链信息, 其中–1表示无跳转对应节点; 第4行, initSlinksToRootChild函数用来初始化根节点的儿子节点的后缀链信息, 同第8–22行代码基本一致, 不再赘述.
在字符集较大的情况下访问节点v时, 如果直接遍历节点中的每个字符会影响算法执行效率, 为此, 结合后缀树的特点, 本文提出使用子串长度匹配法来实现节点数据的访问. 以图4中的节点1为例, a失配跳转至根节点0, c失配跳转至节点2. 此时节点1还剩下tt长度为2, 由于节点5的长度为2, 且字符t开头, 所以此时只需要添加一个后缀链即可, 无需考虑结尾的t. 第8–22行代码, 从队列中读取当前需要处理的节点位置, 并遍历所有可能的儿子节点, 为其添加后缀链信息. 其中getCharIndex函数用来查找某节点某位置的字符.
2.3 基于后缀自动机的变阶马尔可夫模型后缀自动机(Suffix Automaton, SAM)[17]是一种有向无环词图.
定理1. 设字符串y的长度为n, st(y)为A(y)的状态个数. 对于n=0, st(y)=1; 对于n=1, st(y)=2; 对于n>1, 则可以得到:
n + 1 ≤ st(y) ≤ 2n – 1
并且当且仅当y是abn-1(a, b是不同字符)这种形式的字符串时, st(y)达到上限.
定理2. 设字符串y为非空字符串, ed(y)为A(y)的边数. 可以得到: ed(y) ≤ st(y) + n – 2.
后缀自动机本身是一个DAG(有向无环图), 每个节点表示的是一些可以接收的子串, 并且维护step, right, pre值:
step: 表示该状态能够接受的最长的字符串长度, 一个节点u能表示的子串在字符串中出现的个数为stepu –steppreu.
per: 指向一个能够表示当前状态表示的所有字符串的最长公共后缀的节点. 所有的状态的pre指针构成了一棵树, 恰好是字符串的逆序的后缀树.
right: 表示当前节点的状态, 在原字符串中的出现次数.
2.3.1 后缀自动机的构造算法思想: 长度为N的字符串S, 遍历字符插入到后缀自动机中, 后缀自动机根据规则相应新建节点, 插入后, 利用一个计数排序处理出后缀自动机中所有节点的拓扑序, 后缀自动机的pre指针构成DAG (有向无环图), 因此在拓扑序上具有无后效性, 统计出每个节点的right集大小. 以字符串cactt为例.
1)后缀自动机遍历字符串一次插入, 得到cactt的后缀自动机, 如图6所示.
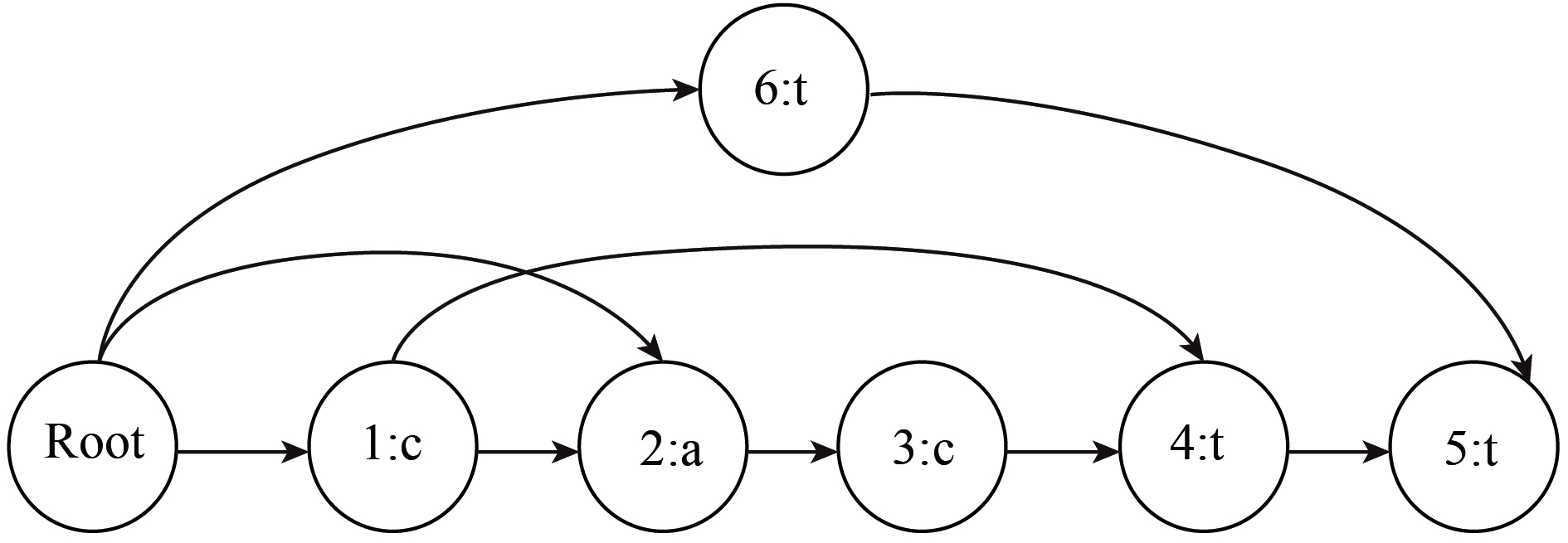
|
图 6 cactt的后缀自动机 |
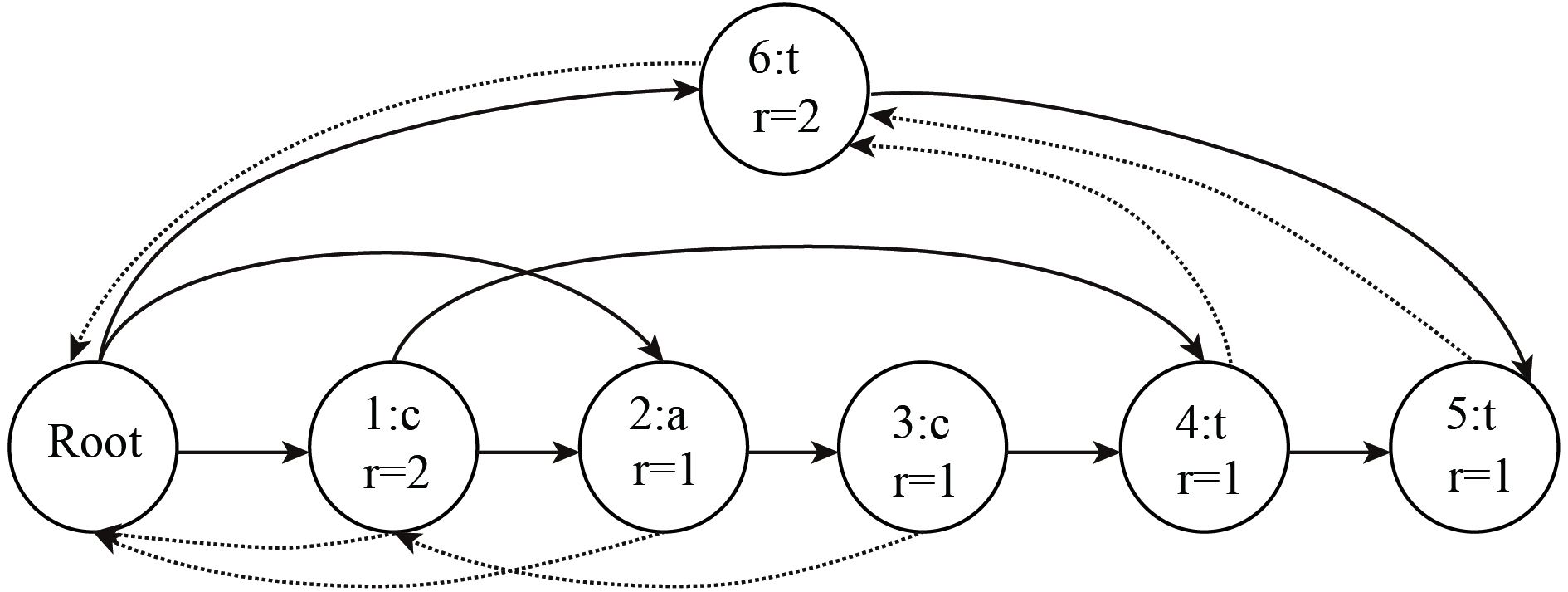
2)后缀自动机中的pre指针由虚线指出, 统计各个后缀自动机的right集大小后, 得到完整的后缀自动机, 如图7所示.
|
图 7 cactt的完整后缀自动机 |
效率分析: 后缀自动机的插入效率是线性的, 利用计数排序得到拓扑序, 以及得到right集大小, 对于每个节点只会遍历一次, 因此总的时间和空间复杂度均为线性的O(|S|).
算法5. BuildSAM (创建后缀自动机)
输入: 训练序列x, 序列长度len
输出: 后缀自动机sam
(1) sz ← 0, last ← 1, node[++sz] ← Node(0)
(2) for i←0 to len–1 do
(3) node[++sz] ← Node(node[last].step + 1)
(4) node[sz].right ← 1
(5) p ← last, np ← sz
(6) while p and !node[p].to[x[i]] do
(7) p ← node[p].pre
(8) node[p].to[c]←np
(9) if !p do
(10) node[np].pre ← 1
(11) else do
(12) q ← node[p].to[c]
(13) if node[q].step ==node[p].step +1 then
(14) node[np].pre← q
(15) else do
(16) node[++sz]← Node(node[p].step +1)
(17) nq← sz
(18) for j ← 0 to sigma_sz do
(19) node[nq].to[j]←node[q].to[j]
(20) node[nq].pre←node[q].pre
(21) node[q].pre←node[np].pre ← sz
(22) while p and node[p].to[c] == q then
(23) p ← node[p].pre
(24) node[p].to[c]=nq
(25) last ← np
(26) topologicalSort()
(27) getRight()
第1行代码对后缀自动机初始化, 生成root节点信息; 第2–25行代码, 根据后缀自动机的字符插入规则更新后缀自动机; 第26行代码, 对构建的后缀自动机中每个节点的step作为参考生成拓扑排序数组; 第27行代码, 按照拓扑排序逆向统计出right集大小.
2.3.2 后缀自动机添加后缀链与树形结构的字典树和后缀树相比, 后缀自动机较为特殊, 后缀自动机的每个节点存放一些字符串可以接受的后缀串, 构造后缀自动机时pre指针, 指向与当前节点所表示可以接收的公共后缀最长的节点, 可以实现快速跳转到下一个可以匹配的后缀串节点, 因此后缀自动机的pre指针可以用来替代后缀链.
3 实验与分析 3.1 实验环境介绍实验硬件平台为: Intel(R) Core(TM) i5-4200H CPU 2.8 GHz (4 CPUs), 内存为12 GB. 软件平台为win 10, VisualStudio, C++语言. 实验DNA数据集, 从http://www.ncbi.nlm.nih.gov/(一个DNA基因数据库)中, 下载几类DNA数据. 对于同一类的DNA通过拼接的方法, 得到DNA长度为 1000、10 000、100 000、1 000 000、10 000 000级别的样本数据.
3.2 算法时空复杂度对比1)理论分析
根据前文对几种不同算法的理论分析和伪代码描述, 算法的时间、空间复杂度对比情况如表5所示.
2)实验结果分析
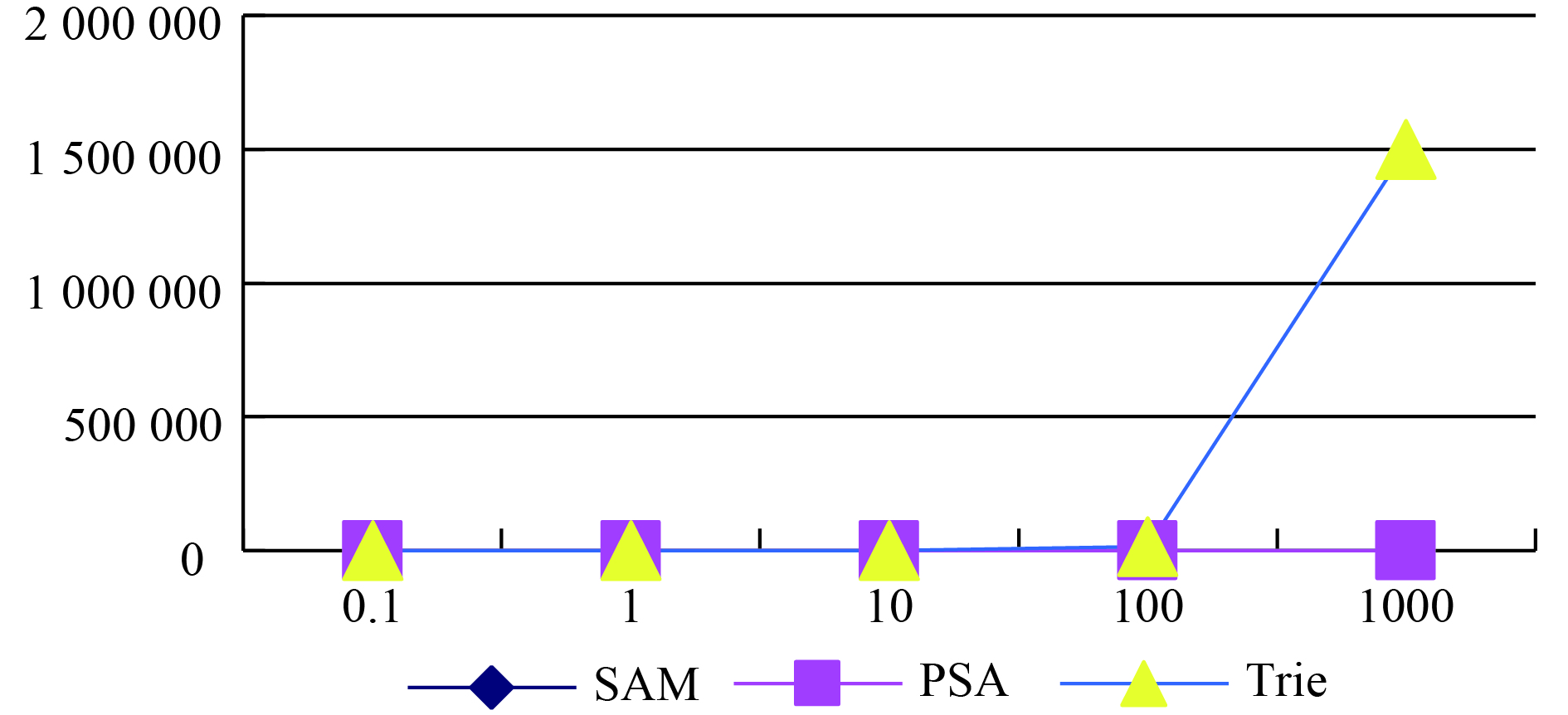
分别实现几种不同算法, 在相同数据集下, 测试结果如表6、表7及图8至图11所示.
| 表 5 不同算法的时空复杂度对比 |
| 表 6 不同模型训练耗时对比分析(单位: s) |
| 表 7 不同模型训练空间消耗对比分析 |
|
图 8 3种算法的时间消耗对比图 |
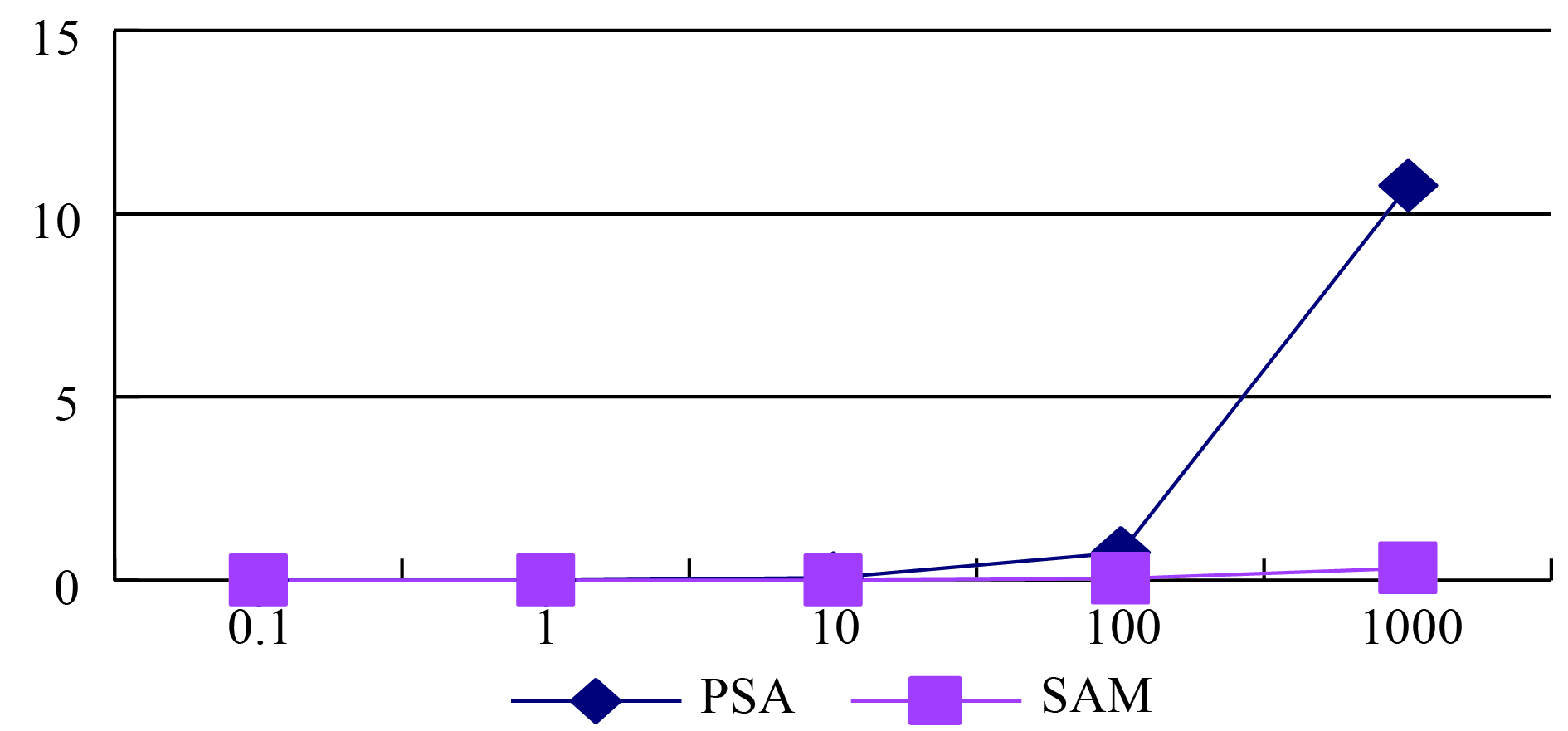
|
图 9 两种线性算法的时间消耗对比图 |
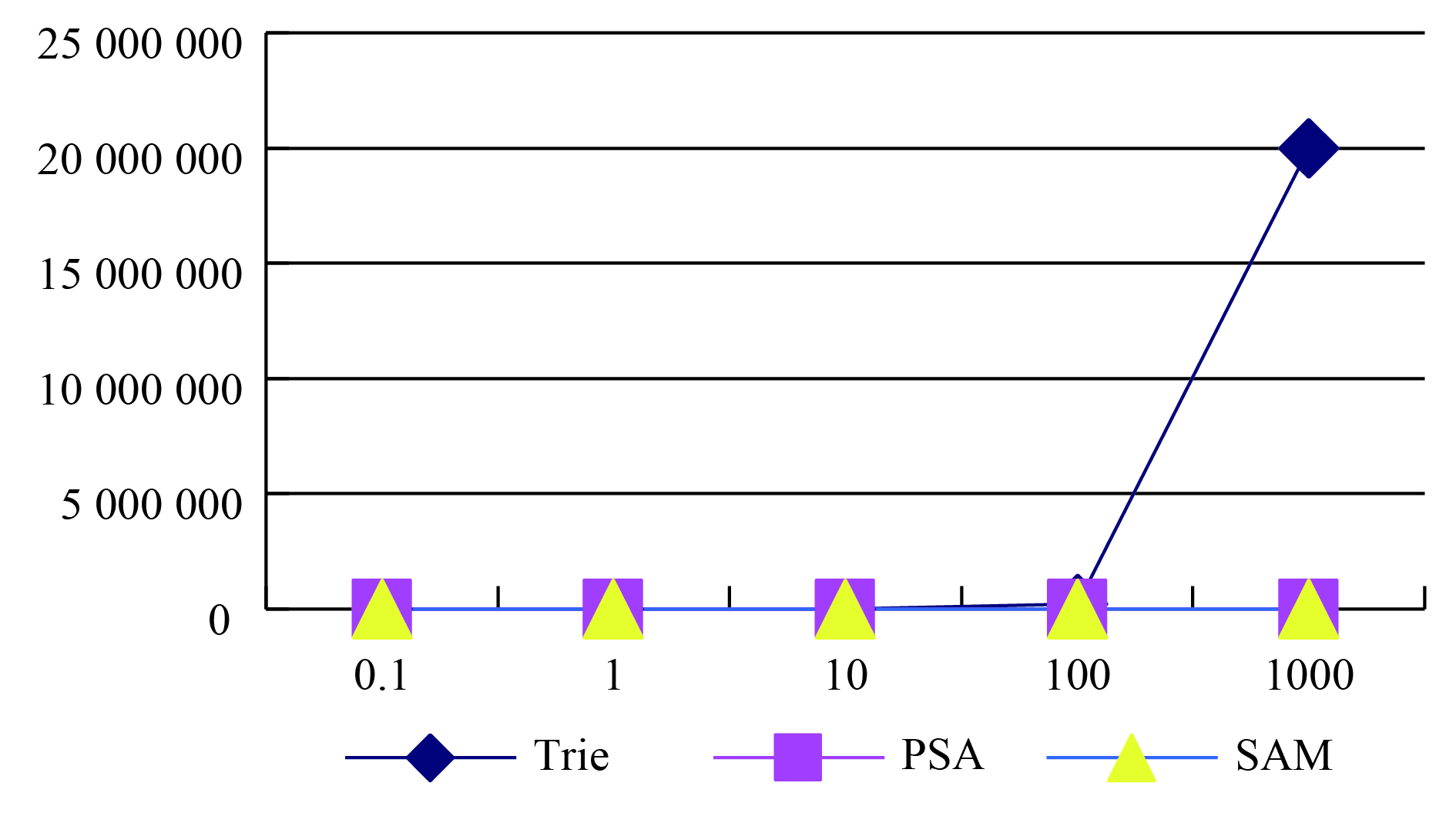
|
图 10 3种算法的空间消耗对比图 |

|
图 11 两种线性算法的空消耗对比图 |
通过以上图表分析可知, 由于字典树的时空复杂度均为O(N2), 随着训练数据的增加, 出现时空消耗膨胀问题, 因此字典树构造动阶马尔科夫模型更适用于小数据的情形下. 后缀树与后缀自动机的时间空间复杂度均为线性的O(N), 由于后缀树算法过程较为复杂, 过程中运算常数较大, 效率上稍微劣于后缀自动机, 但是后缀树的实现方式更为直观易懂并且易于描述, 并且同样也是一个线性的实现方法, 可作为动阶马尔科夫模型的一个高效实现方法.
4 结束语马尔科夫模型是一种适用性广的概率统计模型, 广泛运用在语音识别、生物序列分析、位置预测等领域, 具有重要意义. 本文分析了传统马尔科夫模型存在的局限性, 对相关理论知识进行研究探讨, 从后缀结构的角度, 提出了基于后缀数组和后缀自动机的变阶马尔科夫模型实现算法, 给出了算法的设计思想和复杂度分析过程, 以DNA数据集进行对比实验, 实验表明, 算法能在线性时间和空间复杂度内构建模型, 有效解决传统马尔科夫高阶模型状态空间膨胀问题, 具有较好的效率, 能为在线建模学习和应用提供解决方案. 下一步工作将从两个方面展开研究, 一方面是将模型应用到相关的领域, 如交通数据处理, 购物模式, 公众出行规律研究等. 另一方面是从大数据建模的角度, 引入分布式计算平台, 实现基于Hadoop和Spark框架下的并行计算算法, 进一步提高算法的计算能力, 为大规模的数据挖掘和分析提供基础.
| [1] |
Wang BN, Hu YH, Shou GC, et al. Trajectory prediction in campus based on Markov chains. In: Wang Y, Yu G, Zhang YY, et al. eds. Big Data Computing and Communications. Cham: Springer, 2016.
|
| [2] |
Illescas G, Martínez M, Mora-Soto A, et al. How to think like a data scientist: Application of a variable order Markov model to indicators management. In: Mejia J, Munoz M, Rocha Á, et al. eds. Trends and Applications in Software Engineering. Cham: Springer, 2016.
|
| [3] |
Goreac D, Kobylanski M, Martinez M. A piecewise deterministic Markov toy model for traffic/maintenance and associated Hamilton-Jacobi integrodifferential systems on networks. Applied Mathematics & Optimization, 2016, 74(2): 375-421. |
| [4] |
Asahara A, Maruyama K, Sato A, et al. Pedestrian-movement prediction based on mixed Markov-chain model. Proceedings of the 19 th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Chicago, IL, USA. 2011. 25–33.
|
| [5] |
Gambs S, Killijian MO, del Prado Cortez MN. Next place prediction using mobility Markov chains. Proceedings of the 1st Workshop on Measurement, Privacy, and Mobility. Bern, Switzerland. 2012. 3.
|
| [6] |
Rissanen J. A universal data compression system. IEEE Transactions on Information Theory, 1983, 29(5): 656-664. DOI:10.1109/TIT.1983.1056741 |
| [7] |
Ron D, Singer Y, Tishby N. Learning probabilistic automata with variable memory length. Proceedings of the 7 th Annual Conference on Computational Learning Theory. New Brunswick, NJ, USA. 1994. 35–46.
|
| [8] |
Chin YS, Chen TL. Minimizing variable selection criteria by Markov chain Monte Carlo. Computational Statistics, 2016, 31(4): 1263-1286. DOI:10.1007/s00180-016-0649-3 |
| [9] |
Melikov AZ, Ponomarenko LA, Bagirova SA. Markov models of queueing-inventory systems with variable order size. Cybernetics and Systems Analysis, 2017, 53(3): 373-386. DOI:10.1007/s10559-017-9937-3 |
| [10] |
Nagata Y. Population diversity measures based on variable-order Markov models for the traveling salesman problem. Proceedings of the 14 th International Conference on Parallel Problem Solving from Nature. Edinburgh, UK. 2016. 973–983.
|
| [11] |
Mao B, Cao J, Wu ZA, et al. Predicting driving direction with weighted Markov model. In: Zhou SG, Zhang SM, Karypis G, eds. Advanced Data Mining and Applications. Berlin Heidelberg: Springer, 2012. 407–418.
|
| [12] |
Chen M, Liu Y, Yu XH. Predicting next locations with object clustering and trajectory clustering. In: Cao T, Lim EP, Zhou ZH, et al. eds. Advances in Knowledge Discovery and Data Mining. Cham: Springer, 2015. 344–356.
|
| [13] |
Bejerano G, Yona G. Variations on probabilistic suffix trees: Statistical modeling and prediction of protein families. Bioinformatics, 2001, 17(1): 23-43. DOI:10.1093/bioinformatics/17.1.23 |
| [14] |
Leonardi FG. A generalization of the PST algorithm: Modeling the sparse nature of protein sequences. Bioinformatics, 2006, 22(11): 1302-1307. DOI:10.1093/bioinformatics/btl088 |
| [15] |
Apostolico A, Bejerano G. Optimal amnesic probabilistic automata or how to learn and classify proteins in linear time and space. Journal of Computational Biology, 2004, 7(3–4): 381-393. |
| [16] |
Lin J, Adjeroh D, Jiang BH. Probabilistic suffix array: Efficient modeling and prediction of protein families. Bioinformatics, 2012, 28(10): 1314-1323. DOI:10.1093/bioinformatics/bts121 |
| [17] |
Lothaire M. Applied Combinatorics on Words. Cambridge: Cambridge University Press, 2005.
|
 2018, Vol. 27
2018, Vol. 27



