图像匹配是目标跟踪、图像检索和图像全景拼接等多个应用领域中重要的组成部分^[1–4]. 目前匹配算法主要是基于图像特征学习的, 该类方法对于复杂环境的图像匹配仍能保持较好的稳定性, 已逐渐成为图像匹配研究的主流方向.

SIFT算法^[5]是公认性能最好的特征匹配算法之一, 适用于图像的尺度、旋转变换、光线强弱变化等各种复杂情况下. 但是算法的复杂度较高, 影响特征点的检测速度和匹配速度. 快速鲁棒特征(SURF)算法^[6]是对SIFT的改进, 该算法采用海森矩阵, 使特征点的检测速度提高几倍, 但降低了匹配准确率. PCA-SIFT算法^[7], 其思想是用主元分析法^[8]代替SIFT算法中直方图方法, 提高算法运行的速度, 但匹配数目较少. 近年来也产生了一些性能较好的算法, 如Xu等^[9]是将局部轮廓信息和全局信息融合, 并结合改进的DTW技术, 通过计算全局最佳匹配路径, 能够实现局部匹配. Chen等^[10]通过基础矩阵计算特征点极线, 并通过极线约束剔除错误匹配. Ren等^[11]是将彩色信息和灰度信息叠加, 形成改进的SURF特征描述子, 并采用双向搜索策略实现特征匹配.

特征匹配时, 无论是最佳路径的选择, 还是采用双向搜索策略, 都会有效提高匹配正确率. 但是多数匹配算法是对图像进行全局特征点检测, 而且特征匹配时使用全局搜索策略, 也会影响算法运行速度. 针对上述问题, 提出一种基于稀疏结构的图像特征匹配(Sparse Structure Matching, SSM)算法. 通过分析每个像素点的稀疏度值, 筛选出稀疏度高的像素点所在的区域, 作为结构稀疏度区域, 缩小特征点的提取范围, 加快特征点检测的速度, 并通过最佳描述子的选择实现特征匹配.

1 SSM算法

SSM算法是在特征点提取之前, 通过稀疏度值的高低筛选出结构区域, 然后对结构区域进行特征提取, 这样就避免了在全局进行特征点提取, 减少了一些不稳点特征点的数量, 这就使特征点生成过程, 缩短特征点检测时间, 且采用最佳描述子匹配的准确率得到有效提高.

1.1 稀疏函数

在图像中一个较小邻域的灰度发生急剧的变化, 其实体现的就是图像的结构. 而灰度变换和空间变换对局部结构的影响较小^[12]. 一般图像的轮廓、图形的拐角、交叉区域包含了图像中大部分结构. 在图像中, 一个图像块与其邻域中的其余图像块之间一般存在一定的联系.

如图1所示, 其中, 图像块用实线框区域表示, 其邻域用虚线框区域表示. 图中A位于图像中平滑区域, 其邻域内有较多的相似图像块^[13]. 而位于图像中结构区域的B, 其邻域范围内有很少的相似图像块.

Xu等^[14]根据图像中图像块和它邻域内其它图像块之间的一个相似度, 来定义图像稀疏结构的概念. 对图像全局进行图像块的划分, 假设将图像中某一像素点m为中心的邻域窗口记为N(m), 其大小为25×25. 以该像素点为中心的图像块记为ψm, 其大小为7×7, ψm_i是其邻域窗口中以m_i为中心的邻域块, 领域窗口N(m)中所有的m_i的集合记为Ns(m), 即:

${N_s}(m) = \{ {m_i}:{m_i} \in N(m)\;\;{{and}}\;\;{\psi _m}_i\} $

(1)

直方图能够反映图像的灰度分布, 以直方图计算相似度, 复杂度低. 梯度信息反映了相邻像素之间的相对变化、连接紧密程度以及图像的方向特征, 所以引用文献[15]中的梯度信息相似性度量, 将梯度信息与直方图相似性度量结合, 增加衡量图像块位于结构区域的可信度, 计算图像块的直方图, 则不同图像块直方图之间的相似性定义为:

$H\left( {m,{m_i}} \right) = \frac{1}{{l + 1}}\sum\limits_{i = 0}^{i = l} {\left| {h{1_i} - h{2_i}} \right|} $

(2)

式(2)中, H(m, m_i)表示图像块ψ_m的直方图和邻域范围中其余图像块ψ_mi的直方图的相似度, h1_i表示图像块ψ_m灰度级为i时的像元个数, h2_i表示图像块ψ_mi灰度级为i时的像元个数, 灰度级l=255. 两图像块相似度越高, 其直方图越相似, 那么H(m, m_i)的值就越小.

如图1中A的邻域内图像块C和A比较相似, 其直方图之间的相似度较高; 而D则与A相差较大, 其直方图之间相似度较低, 所以采用直方图的方法能够较好的衡量图像块之间的相似度.

图像块ψ_m与图像块ψ_mi之间的相似度定义为:

${M_m}{,_m}_i = \frac{1}{{p(m)}}\exp ( - \frac{{d({\Gamma _m},{\Gamma _{{m_i}}}){{ + }}H({\psi _m},{\psi _{{m_i}}})}}{{{\alpha ^2}}})$

(3)

式(3)中, d(Г_m, Г_mi)表示在梯度模值图像中, 以m与m_i为中心的图像块间的距离, α=5, 用来控制相似度的衰减程度. P(m)是归一化系数, 使: $\sum\limits_{{m_i} \in {N_s}(m)} {{M_m}{,_{{m_i}}}} = 1$ .

在求得图像块之间的相似度之后, 图像块的稀疏度函数就可以定义为:

$S(m) = \sqrt {\left[ {\sum\limits_{{m_i} \in {N_s}(m)} {M_{m,{m_i}}^2} } \right]\frac{{|Ns(m)|}}{{|N(m)|}}} $

(4)

式(4)中, |Ns(m)|是集合中元素个数; |N(m)|表示邻域窗口中元素的个数.

1.2 稀疏结构区域的标记

通过对图像分析, 由稀疏度函数求解出每个图像块的稀疏度值S(m), 利用块结构稀疏概念将图像划分为两类^[16]: 一是包含大量结构信息的结构区域, 称为结构块; 二是包含大量纹理信息或平滑区域的非结构区域, 称为非结构块. 图像中结构区域、非结构区域的结构稀疏度是不同的, 结构区域的结构稀疏度值较高一般在0.7~1.0之间, 而非结构区域的稀疏度值一般小于0.3.

在运算中, 将阈值设置为0.7, 这样对于不同的图像基本都可以筛选出它们的结构区域. 结构块的稀疏度值都大于规定的阈值, 则为稀疏结构区域, 认定关系表述为:

$S\left( m \right) \ge \xi $

(5)

式(5)中S(m)为图像块的稀疏度值, ξ=0.7为规定的阈值. 相反, 非结构块的稀疏度值都小于规定的阈值. 在一般情况下, 在一幅图像中结构块的数量远少于非结构块的个数, 所以只对标记的结构块进行特征提取, 提取的特征稳定性好且能有效减少处理的区域.

计算每个像素的稀疏度值, 通过定义的阈值, 将稀疏度值高的区域筛选出来, 进行标记, 如图2所示.

1.3 稀疏结构区域的SIFT特征提取

采用SIFT的方法对有标记的稀疏结构区域进行极值点检测、关键点定位和方向分配. 极值点的检测, 如图3(a), 对图像特征方向的定位, 如图3(b)所示.

1.4 最佳描述子选择及特征匹配

通过关键点周围区域梯度信息得到SIFT描述子. 关键点及其周围部分像素点都包含在描述子中, 而图像匹配的质量依赖于特征提取的描述子, 因此如何找到最佳的描述子, 是提高匹配准确率的一种方法. 描述子的有效性不仅取决于图像内的外观, 而且取决于图像间的变化, 因此对于图像匹配, 最佳的描述子通常是图像相关或者是区域相关^[17].

特征匹配是通过在特征点邻域内搜索多个描述子中的一个, 该邻域内所有的描述子就作为候选描述子. 特征点之间距离可能相隔几个像素, 特别是对于邻域内两个相距最近的特征点, 它们的描述子相似度较高, 在对这两点寻找对应匹配点时, 导致错误匹配的概率就会增高. 在邻域内的候选描述子中寻找一个描述子能使该特征点与其相距最近的特征点进行区分, 这样的描述子就是该特征点的最佳描述子. 将最佳描述子选择问题转化为构造图的能量最小化问题.

(1) 构造图

若给定待匹配图像I^p和I^Q, 特征点分别是 ${C^p} = \left\{ {C_i^p} \right\}_{i = 1}^{{N^p}}$ 和 ${C^Q} = \left\{ {C_i^Q} \right\}_{i = 1}^{{N^Q}}$ , 构造图G, 由顶点集v和边集ε组成, 表示为G(v, ε). 图G中每个顶点 ${v_i} \in v$ , 在本文中即是对应于图像I^p中的特征点C^p, 顶点的数量|v|=N^p. 如果在某一邻域大小为K的区域中, C_j是距离C_i最近的邻点, 则连接它们对应的顶点v_i和v_j的边为e_ij, 且 ${e_{ij}} \in \varepsilon $ . 复合变量 ${w_i} = \left[ {{s_i},{d_i}} \right]$ , 每个顶点与复合变量相关联, 该复合变量w_i表示通过描述子d_i将特征点 $C_i^p$ 与特征点 $C_{{s_i}}^Q$ 进行匹配, 此时选择的描述子d_i, 即是最佳的描述子; 而特征点 $C_i^p$ 与特征点 $C_{{s_i}}^Q$ 是在最佳描述子下的最佳匹配对.

(2) 寻找合理的图的标号

图的标号 $W = \left[ {{w_1}, \cdots, {w_i}, \cdots, {w_{{N^p}}}} \right]$ , 指定了在描述子下, 图像I^p中特征点C^p在I^Q中对应的特征点. 可以通过定义最小化能量函数来寻找合理的标号W^[17].

$J\left( W \right){{ = }}\mathop {\min }\limits_{{v_i} \in v} {g_i}\left( {{w_i}} \right)$

(6)

式(6)表示特征点邻域内描述子的评估功率取最小值, ${g_i}\left( {{w_i}} \right)$ 为邻域内选择的描述子的评估功率.

${g_i}\left( {{w_i}} \right) = \frac{{f\left( {i,{w_i}} \right)}}{{\frac{1}{n}\sum\limits_{{e_{ij}} \in \varepsilon } {f\left( {j,{w_i}} \right)} }}{{ = }}\frac{{f\left( {i,{s_i},{d_i}} \right)}}{{\frac{1}{n}\sum\limits_{{e_{ij}} \in \varepsilon } {f\left( {j,{s_i},{d_i}} \right)} }}$

(7)

式(7)中, n是 $C_i^p$ 空间邻域的个数, s_i是特征点索引, d_i是描述子索引. 其中,

$f\left( {i,{s_i},{d_i}} \right) = dist\left( {Y_{i,{d_i}}^p,Y_{{s_i},{d_i}}^Q} \right)$

(8)

式(8)中, Y是特征点的特征向量, $f\left( {i,{s_i},{d_i}} \right)$ 是在描述子d_i下, 特征点 $C_i^p$ 和 $C_{{s_i}}^Q$ 之间的光度相异函数, dist是特征向量之间的欧式距离. 同理, $f\left( {j,{s_i},{d_i}} \right)$ 是在描述子d_i下, 特征点 $C_j^p$ 和 $C_{{s_i}}^Q$ 之间的光度相异函数.

(3) 最佳描述子及特征匹配

当式(6)的取值为最小时, 则选择的这个合理的标号为W=w_i, 故由 ${w_i} = \left[ {{s_i},{d_i}} \right]$ 可知, 邻域内选择的描述子d_i, 是 $C_i^p$ 的最佳描述子, 该描述子下的特征点的匹配是最佳的匹配; 否则, 该描述子就不属于最佳描述子, 这样的描述子无法区分相邻匹配点对 $\left( {C_j^p,C_{{s_i}}^Q} \right)$ 和 $\left( {C_i^p,C_{{s_i}}^Q} \right)$ , 故被舍去.

1.5 算法运行步骤

本文算法步骤如下:

步骤1. 分别将两幅利用式(4)计算图像块的稀疏度值, 用式(5)进行筛选, 得到稀疏结构区域, 对该区域进行标记;

步骤2. 构造尺度空间. 将待匹配图像与高斯核函数卷积可得到待匹配图像的尺度空间, 为:

$L({x_0},{y_0},\sigma ) = G({x_0},{y_0},\sigma ) * I({x_0},{y_0})$

(9)

$G({x_0},{y_0},\sigma ) = \frac{1}{{2\pi {\sigma ^2}}}{e^{ - ({x_0}^2 + {y_0}^2)/2{\sigma ^2}}}$

(10)

式(9)、(10)中, (x₀, y₀)是像素点的位置, σ决定图像平滑程度. 将高斯尺度空间中相邻两层相减得到高斯差分金字塔, 对其特征进行归一化, 可以得到明显的差分图像蕴含的特征, 这些特征就是要提取的稳定特征.

步骤3. 采用经典SIFT算法对两幅图像中有标记的稀疏结构区域中进行极值点检测和关键点定位.

步骤4. 统计关键点邻域的梯度信息生成SIFT描述子.

步骤5. 利用式(7)计算描述子的评估功率, 利用式(6)找到评估功率的最小值. 在最佳描述子下, 将特征点 $C_i^p$ 与 $C_{{s_i}}^Q$ 进行匹配, 对匹配的两特征点进行连线, 直到图像I^p中所有特征点找到其在图像I^Q中的对应匹配点为止.

2 算法测试及结果分析

实验运行环境为Matlab R2014b版本, Intel(R) Core(TM)i5-3210M 2.3 GHz 4 GB内存的PC机. 实验5组图像数据, 分别为cat、flower、lena、build和street, 图像分辨率均为400 dpi.

2.1 匹配结果比较

为验证本文算法的普适性, 使用不同类型的图像, 将SSM算法与三种算法进行比较.

图4是选择5种图像数据的特征匹配结果图, 图中每根线代表一对特征匹配对, 图(a)、(b)、(c)和(d)分别表示SIFT、SURF、PCA-SIFT和SSM算法匹配结果. 从图中可以看出, 图(d)相比于其它算法的匹配对个数较多.

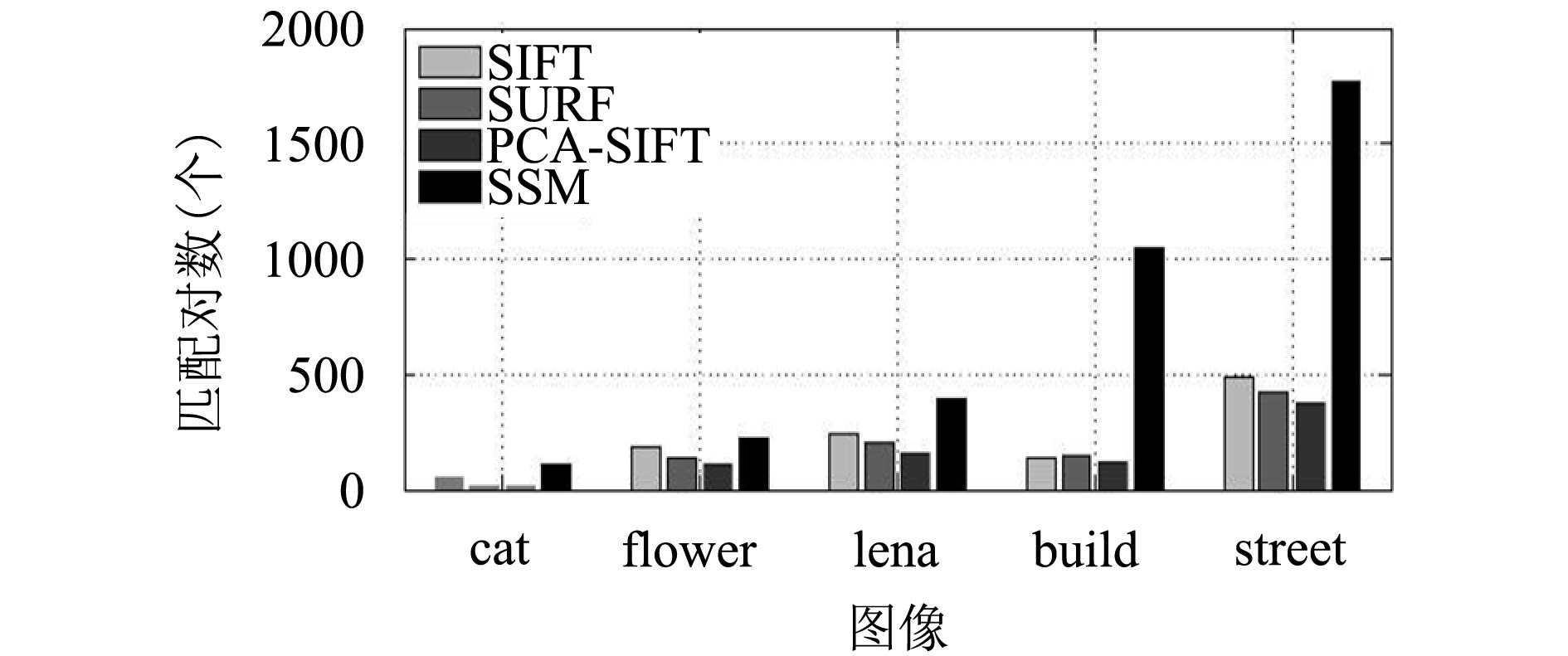
匹配结果数据用表1列出, 可知cat图像的匹配结果中, SSM方法的匹配对数是SIFT方法的2.1倍, 是SURF方法的6.3倍, 是PCA-SIFT方法的8.9倍. flower图像的匹配结果中, SSM方法的匹配对数是SIFT方法的1.3倍, 是SURF方法的1.7倍, 是PCA-SIFT方法的2.0倍. lena图像匹配结果中, SSM方法的匹配对数是SIFT方法的1.6倍, 是SURF方法的1.9倍, 是PCA-SIFT方法的2.5倍. build图像的匹配结果中, SSM方法的匹配对数是SIFT方法的7.7倍, 是SURF方法的7.0倍, 是PCA-SIFT方法的9.2倍. street图像的匹配结果中, SSM方法的匹配对数是SIFT方法的5.7倍, 是SURF方法的6.6倍, 是PCA-SIFT方法的7.5倍. 5组数据中, SSM方法的匹配对个数比其它三种方法高出1.3~9.2倍.

为了直观表明SSM方法的优越性, 画出了四种算法得到的特征点匹配对数的柱状图, 如图5. 可以看出, 对于任意一组图像数据, SSM算法的匹配对数都比其它三种算法多出1.3倍以上. 选择的图像包括: 单个对象、自然景物、建筑物和室外复杂场景, 采用SSM算法, 匹配效果都得到提高, 足以说明SSM算法的普适性.

2.2 匹配速率

为了准确评估SSM算法性能, 分别对图像在亮度、旋转、尺度、加椒盐噪声和仿射变换等复杂情况下进行对比试验, 性能分析中选择lena图像作为试验对象.

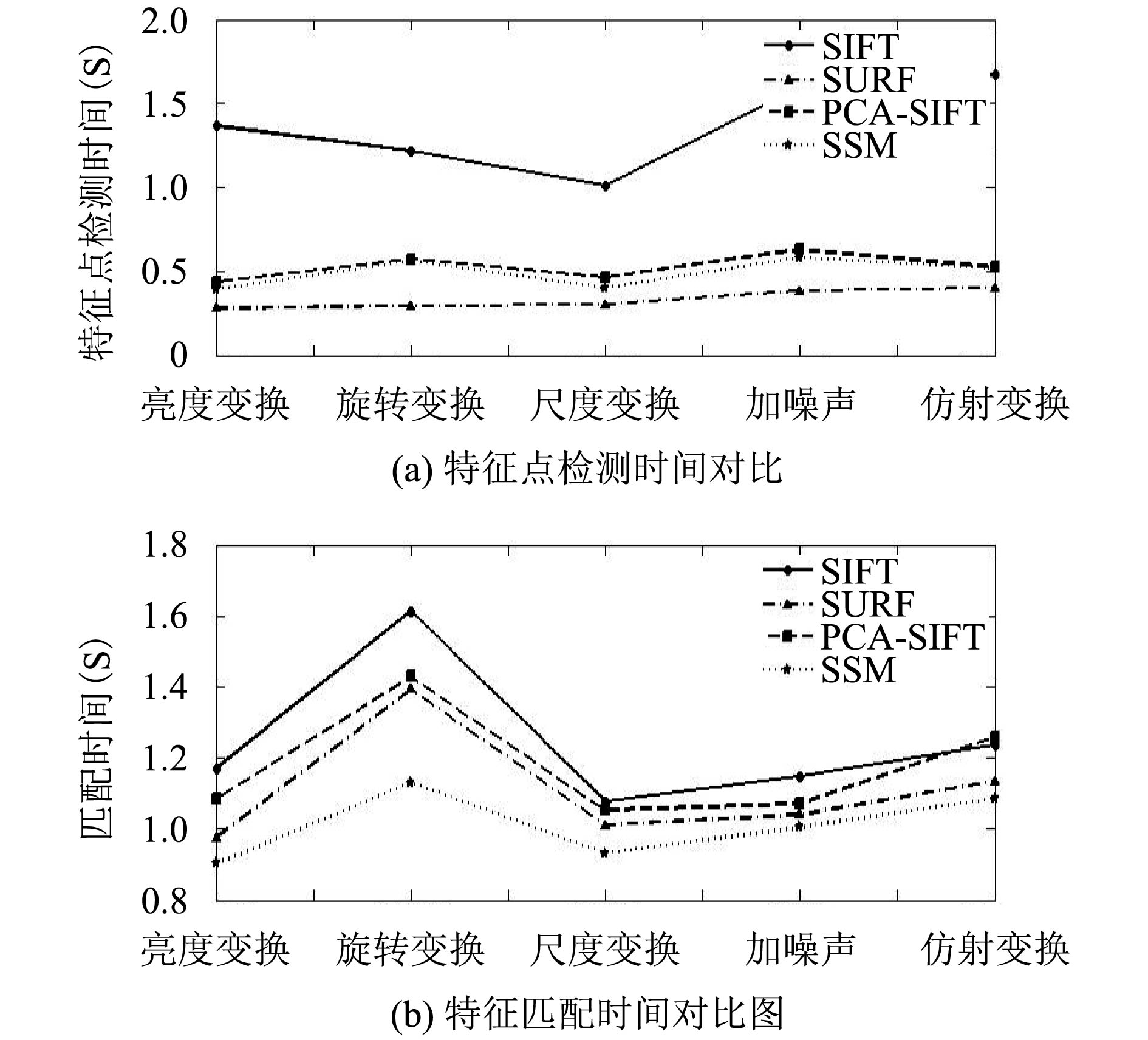
将SSM算法与SIFT、PCA-SIFT、SURF三种方法, 在特征检测时间和特征匹配时间进行比较. 算法运行时间对比, 如图6所示, 由图(a)可以看出, 对于不同的图像变换, 由于SURF通过海森矩阵定位兴趣点, 所以检测耗时最短; 而SSM算法是在稀疏结构区域进行特征点检测, 有效的缩小了检测范围, 但是在寻找稀疏结构区域时也会增加计算复杂度, 虽然在检测速度上优于PCA-SIFT算法和SIFT算法, 但是仍然没有SURF算法检测速度快. 由图(b)可知, SSM算法匹配时间最短, SIFT算法耗时最长. 因为本文方法不是对图像进行全局寻找匹配点, 而是在稀疏结构区域进行全局搜索, 这样就会大大减少搜索区域, 节省很多时间. 而其它三种算法均是对图像进行全局的特征点搜索, 每搜索一个特征点, 都要进行一次步骤5, 要将所有特征点一一匹配也是一个浩大的工程. 所以本文算法在匹配速度上是优于其它三种算法的.

2.3 匹配准确率

为了直观反应算法的匹配效果, 定义了匹配准确率函数P. P越大说明错误匹配对越少, 算法的匹配效果越好. 假设图像I^p和图像I^Q进行特征匹配时, 匹配总数为f, 其中错误匹配数为f₁, 那么匹配准确率可以定义为:

$P = \frac{{f{{ - }}{f_1}}}{f} \times 100\% $

(11)

由表2可以看出, 在图像亮度变换的情况下, SSM算法的匹配准确率为91.5%, 比其它三种算法高6.1%~13.2%, 而SIFT准确率略低. 在图像旋转变换情况下, SSM算法的匹配准确率为98.3%, 比其它三种算法高12.3%~34.6%, SIFT准确率还是相对较高, 而旋转变换对SURF和PCA-SIFT的影响较大. 在图像尺度变换的情况下, SSM算法的匹配准确率为98.6%, 比其它三种算法高8.5%~19.4%, SURF和PCA-SIFT的匹配准确率相对较低, 而SIFT的匹配准确率是图像几种变换下最高的, SIFT具有较好的尺度不变性. 在图像加噪声的情况下, SSM算法的匹配准确率为97.8%, 比其它三种算法高11.1%~36.1%, 而噪声对SIFT的影响较大. 在仿射变换下, SSM算法的匹配准确率为90.2%, 比其它三种算法高9.9%~15.8%. 由于SSM算法特征点稳定性较好, 且采用最佳描述子下进行特征匹配, 所以受图像外界影响较小. 因此在图像进行复杂变换时, SSM算法在匹配准确率上比其它三种算法更具有优势.

3 结论

针对传统特征匹配算法特征点检测耗时长和匹配准确率低的问题, 本文提出一种基于稀疏结构的图像特征匹配算法. 文中通过引入稀疏结构的概念, 进而考虑到在稀疏结构区域提取特征点以缩小特征点的检测范围. 通过对实验结果的分析, 我们可以看出, 本文提出的SSM算法与其它的算法相比, 无论在特征点的检测速度, 还是在特征匹配速度, 更或者是匹配准确率和算法普适性方面, 都具有很好的优势. 但是本文算法也存在一些不足, 比如在计算稀疏度值、筛选出稀疏度高的像素点所在的区域上, 比其它的算法稍显复杂. 接下来的研究工作主要在两个方面: 一是考虑到该方法存在一定的错误匹配, 如果与误匹配剔除结合起来, 会使算法性能更好. 二是将本文算法与目标跟踪算法相结合.