图像中的角点是图像的重要特征, 具有旋转不变性, 决定了图像形状, 可以降低图像信息的存储效率, 在目标跟踪, 目标检测, 图像匹配, 图像轮廓拟合等领域都有重要的应用价值. 近几十年来, 国内外学者提出的图像角点检测算法[1], 各有各的优缺点, 大致可分为三大类: 基于灰度强度的角点检测、基于模型的角点检测、基于边缘轮廓的角点检测[1]. 基于灰度强度的方法是通过图像的一阶或二阶导数查找, 经典算法代表有Harris算法[2], Harris算法通过微分运算和自相关矩阵来检测角点, 稳定性高, 但是高斯平滑函数的窗口可控性差, 定位精度较差[3].基于模型的方法是通过将一小块图像与预定义的模型相匹配来查找角点, SUSAN算法[4]就是这类角点检测的代表, SUSAN通过一个圆形模板实现角点检测, 通过模板中所有与圆心点像素相似的点组成的区域大小判断角点, 该算法不对图像求导, 精度较好, 具有一定的抗噪性, 但是相似函数计算较复杂, 且需要人工设定阈值[4]. 基于边缘轮廓的方法主要是通过分析图像边缘形状来检测角点的, 包括五个步骤[1]: 边缘提取和选择、曲线平滑、曲率估计、检测角点和角点跟踪筛选出最终的角点. 近年来, 基于边缘轮廓方法吸引了广泛的关注, 许多此类优秀的角点检测算法被提出[5]. 1998年Mokhtarian等人提出的著名CSS角点检测算法[4], 利用Canny边缘检测算子提取图像边缘, 从边缘中提取边缘轮廓, 并填充边缘轮廓缺口, 在大尺度下得到轮廓曲率极大值点, 通过阈值选定候选角点, 大尺度到小尺度下对候选角点重新定位, 比较T-角点与曲率极大值检测的角点, 剔除相距相近的点, 该算法获得良好的角点检测效果. 但CSS有两个主要的问题[6], 一是曲率估计对对轮廓局部变化和噪声较为敏感, 二是很难选择合适的高斯尺度平滑边缘轮廓. 在CSS基础上, 通过考虑检测中局部曲率, He和Yung[7]提出了一种使用自适应曲率阈值和动态支撑区域的检测器. 随后Awrangjeb和Lu利用点到弦的距离累加技术提出了一种稳健的角点检测算法——CPDA[8], CPDA具有较高的可重复性和较低的定位误差. 之后又提出了CPDA的快速算法[9]. 但CPDA有一个缺点是估计拐角的曲率值与角度可能不成正比[5]. 还有一些角点检测算法, 利用Freeman链码多边形近似方法查找角点, 两边的交点判定为角点[1], 文献[10]对疑似角点统计链码做进一步筛选角点, 但文献中的方法先使用的是CSS角点检测算法, 仍有曲率计算和角点阈值选取问题, 并且时间复杂度较高; 文献[11]通过判断待定角点前后三个点的Freeman链码是否相同进行检测, 该方法造成错误角点较多, 且文中方法过于繁琐.
本文在文献[10,11]的启发下, 优化文献[11]的链码分析方法, 同时引入文献[10]的链码统计思路, 提出一种新的角点检测算法: 提取图像边缘轮廓Freeman链码, 分析链码发生变化时连续多个点的码值是否符合一定的规则来判定角点. 该算法将链码分析和链码统计相结合, 不仅使得算法变得更加简便, 而且避免了传统方法中轮廓曲率计算和阈值选取, 通过实验结果得出本文算法对于图像角点检测结果准确性高, 具有良好稳健性.
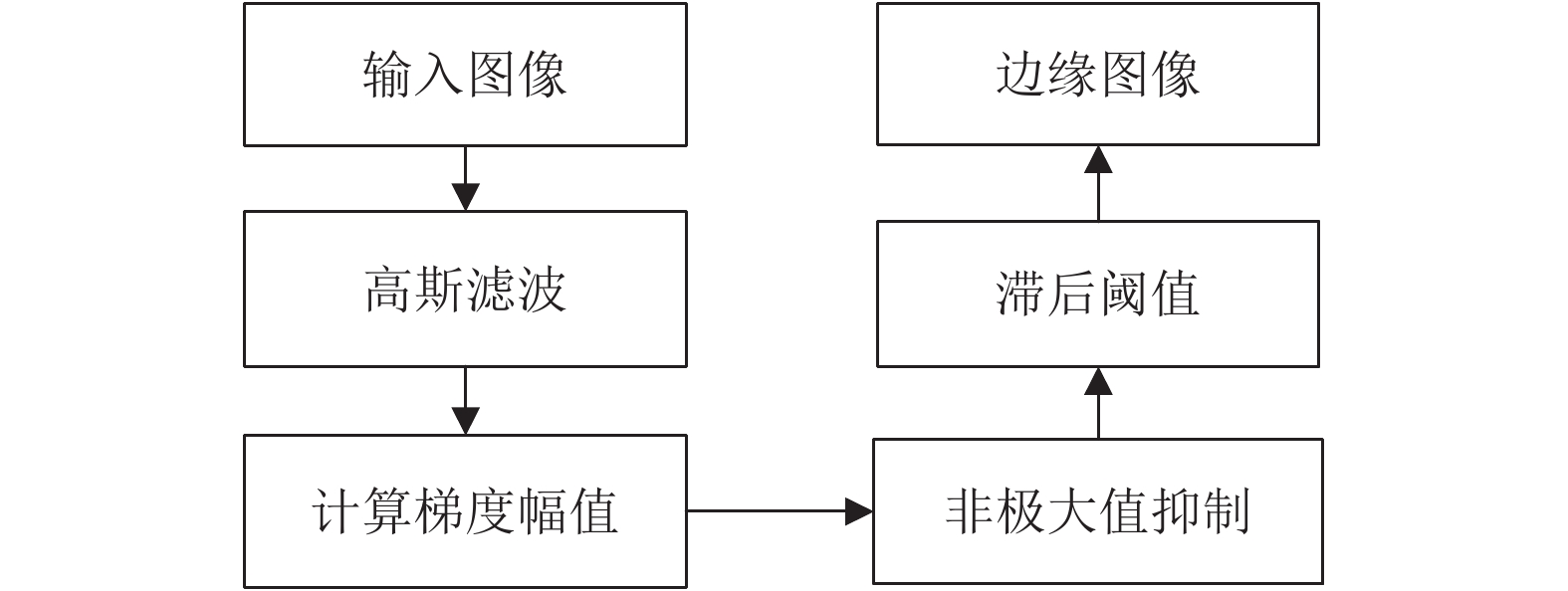
1 Freeman链码生成 1.1 图像预处理本文图像在预处理方面与文献[5]一致采用Canny算法[12]检测边缘, Canny算法抑制了多响应边缘, 提高边缘的定位精度, 具有一定的抗噪能力. Canny算法检测边缘的步骤如图1.
|
图 1 Canny边缘检测步骤 |
1.2 Freeman链码
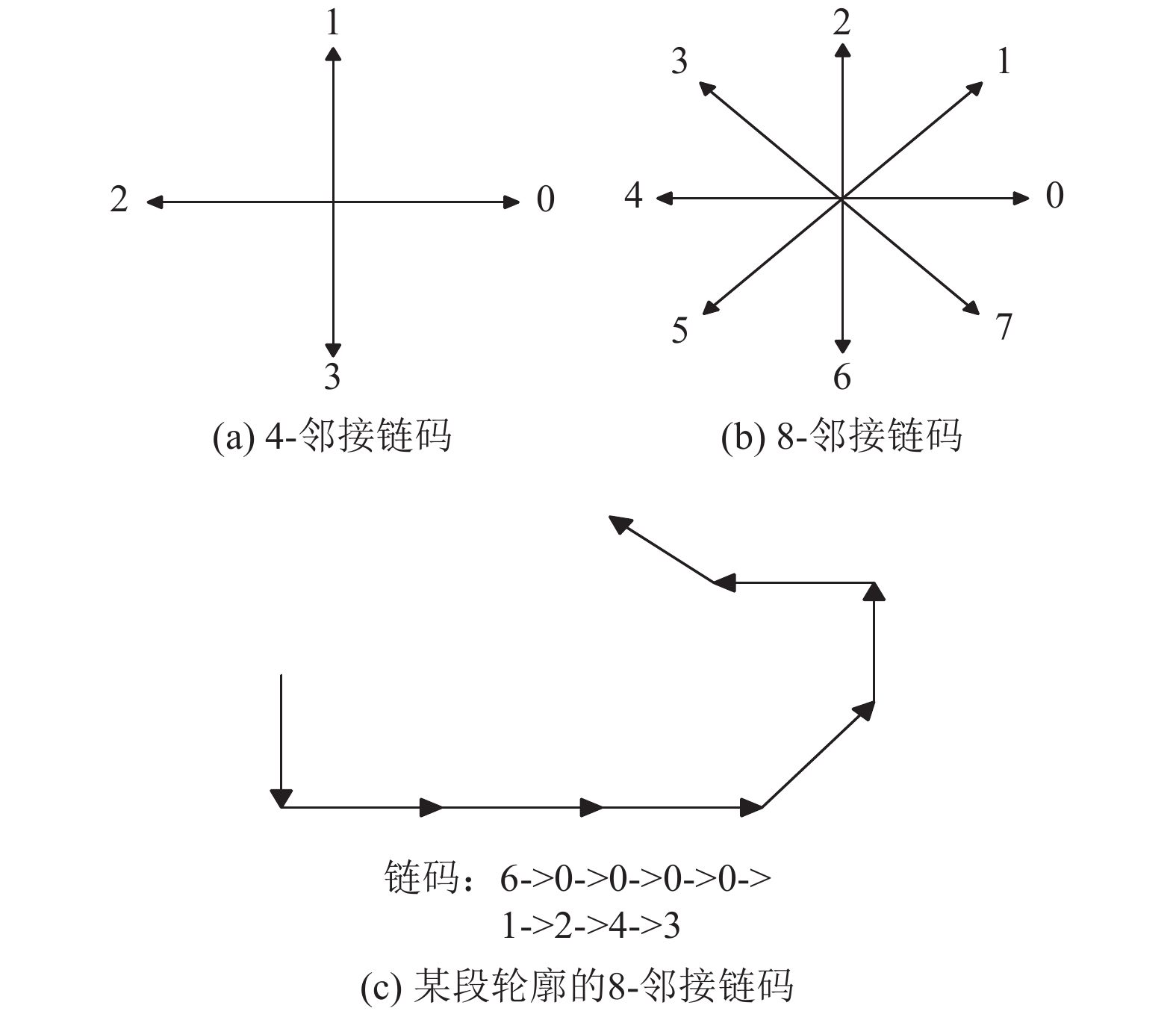
链码是通过带有给定方向的单位长度的线段序列来描述轮廓的边界, 链码的表示方法有基于4-邻接和8-邻接[12], 如图2(a)和图2(b)所示, 8-邻接链码比4-邻接链码增加了4个斜方向, 而较多的基于Freeman链码的算法[10–13]都采用8-邻接来表示链码. 在实际应用中, 边界跟踪法[12]产生轮廓的链码, 4-邻接检测边界只需要搜索4个方向, 8-邻接则需要搜索8个方向, 我们实验所用图都是点阵图, 当轮廓是一条直线时, 4-邻接链码要比8-邻接链码要快捷的多; 当轮廓是一条斜边时, 用4-邻接链码只能搜索上下左右4个方向, 表示轮廓时会丢失大量的边缘信息, 而8-邻接链码正好与像素点的实际情况相符, 能够准确地描述中心像素点与其邻接点的信息, 能较好地保留轮廓边缘信息. 因为任意一个像素周围均有8个邻接点, 因此本文算法采用的是8-邻接链码.
|
图 2 链码示意图 |
一条轮廓曲线Freeman链码可以定义为:
基于八邻域边界跟踪可以得到轮廓的Freeman链码, 轮廓跟踪[13]方法如算法1.
算法1. 轮廓跟踪生成Freeman链码算法.
1) 分轮廓搜索, 找到图像最左上角的一个边界轮廓点P0作为搜索起点, 并以链码值dir=0为最开始搜索方向;
2) 按八邻域的逆时针方向搜索起点的下一个点, 每搜索一次链码值方向逆时针旋转45°, 即dir+1; 如果搜索到新的边界点Pi, 将该链码值赋值给它前一个点即点Pi–1的方向, 再以此点为八邻域的中心点, 链码值方向顺时针旋转90°, 即dir–2作为该点的开始搜索方向, 继续搜索;
3) 重复2)搜索方法, 当搜索到起始点P0时, 整个轮廓搜索完毕.
通过上述轮廓跟踪算法就得到了边缘轮廓的Freeman链码, 我们假定逆时针为正方向, 分轮廓将轮廓点坐标和链码值存储, 存储FMP格式有如下的定义:
struct FMP
{
int x; //点的图像x坐标
int y; //点的图像y坐标
int a; //下一个点的方向
}
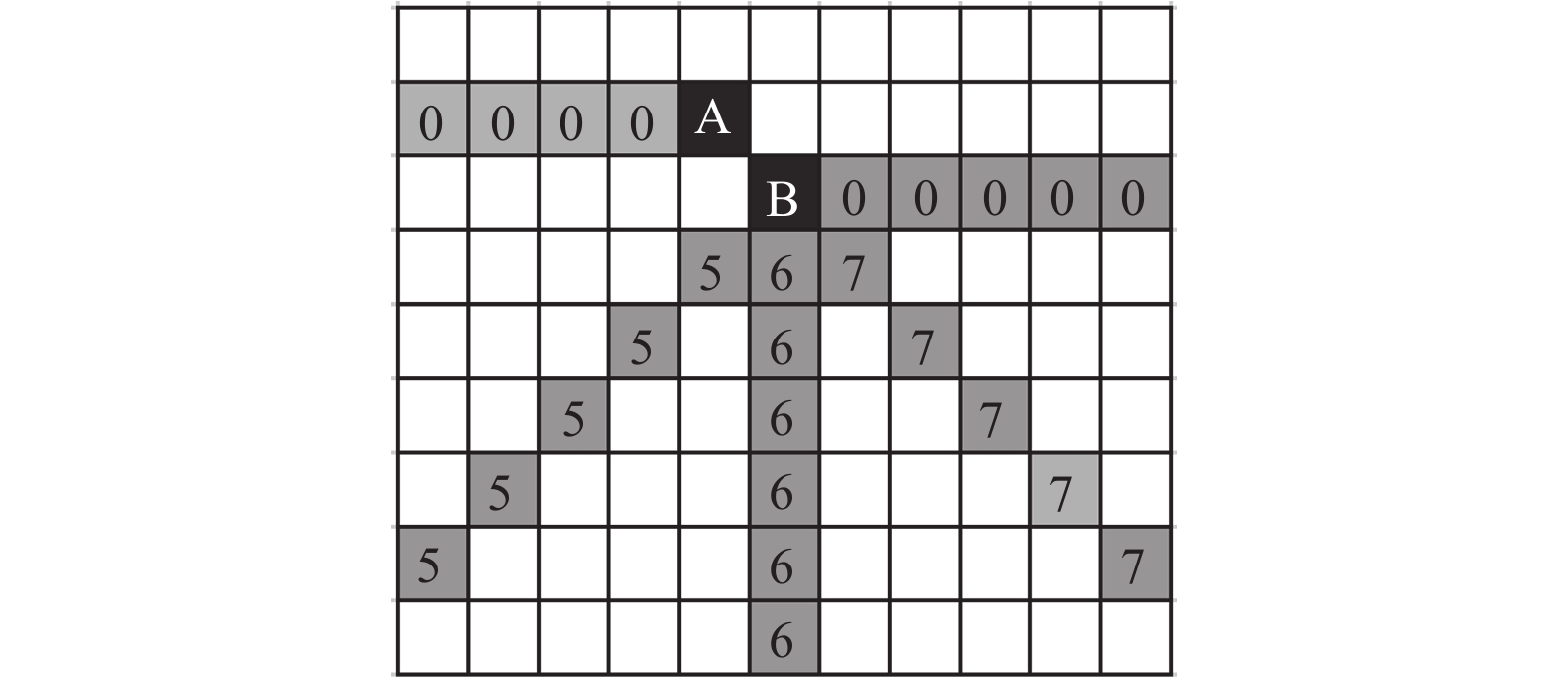
2 对Freeman链码方向分析进行角点检测文献[11]通过对真实角点周围的几个点的Freeman链码分析, 文中分析出要想成为一个真实角点, 分情况讨论了前后连续的三个点的链码值是否相同, 相同则为角点, 不相同则不是角点, 但这样检测出角点误检漏检点较多, 且分析方法较为繁琐; 而文献[10]在改进CSS角点检测之后利用链码统计思路, 统计疑似角点周围几个点的链码值相同的点数再做进一步的判断, 较好地排除了一些错误角点, 但算法时间复杂度较高, 依然存在曲率计算和阈值选取问题. 本文算法在链码分析上做了较大的改善, 同时结合了链码统计思路, 提出了链码分析规则1 . 如图3所示, A点有可能是角点, A的链码值为7, 此时有4种情况: 如果B点之后的链码序列是{00000}, 那么A点就不是角点, 视为一条斜线的一点; 如果B点之后的序列是{77777}, 那么A点视为两条夹角为135°的直线的交点, 如果B点之后的序列是{66666}, 那么A点也视为两条夹角为90°的直线的交点;如果B点之后的序列是{55555}, 那么A点也视为两条夹角为45°的直线的交点, 后3种情况都是角点, 这里的4种情况包含了文献[11]中提及的所有情况的分析.
|
图 3 疑似角点周围点的方向 |
由于A点的链码值为7, 角点符合上述3种情况的链码序列值分别为7, 6, 5. 综上总结, 本文提出下述规则.
规则1. 如果某一个真实角点存在, 那么它的前后几个点的链码方向与它的链码方向夹角都是小于或者等于90°.
2.1 算法基本思路本文算法角点检测思路如下:
(1) Canny算法进行图像边缘检测;
(2)轮廓跟踪法得到轮廓的Freeman链码;
(3)根据图像轮廓点的链码, 求出该轮廓所有点的链码差di[11];
(4)对于凸起或者凹陷处轮廓点进行链码修复;
(5)分析链码发生变化的点的周围多个链码: (a)对于
轮廓链码差[11]即轮廓曲线上的点和它的前一个点的链码方向之差, 定义数组
| ${d_{{i}}}=\left\{ \begin{array}{*{20}{l}}{f(i),}&{{{if}}\;\;(|f(i)| \le 4)}\\{f(i) + 8,}&{{{if}}\;\;(|f(i)| > 4 \& \& f(i) \le 0)}\\{f(i) - 8,}&{{{if}}\;\;(|f(i){{|}} > 4 \& \& f(i) > 0)}\end{array}\right.$ | (1) |
其中
计算得到的
(1)
(2)
(3)
(4)
(5)
在轮廓曲线中, 由于噪声使得在轮廓查找中或多或少有些像素点出现误差. 例如原本一段直线中某像素点突然的凸起或者凹陷, 会造成角点检测错误或漏检, 需要将链码进行修复. 如图4, 为了便于计算, 这里只是进行链码简单修复.

|
图 4 轮廓的凸起点 |
处理过程: 判断变化点是否为凸起点, 若为凸起点, 则进行链码修复, 并修改对应的
为了修复凸起点的链码, 设计了算法2.
算法2. 凸起点链码修复的算法.
1) 输入所有轮廓FMP, 轮廓索引号index;
2) 循环判断di是否等于±2, 如果不等于, 则判断下一个di;
3)如果di等于±2, 需要进一步判断a(i–2)是否等于a(i+1), 如果相等, 则将a(i–2)的值赋值给a(i)和a(i–1), 同时d(i–1)和di都赋值为0.
4) 当所有点都修复完, 则循环结束.
2.2.3 根据链码差分析出角点循环判断
对所有轮廓FMP的每一条轮廓(FMP[index].size>20,index表示轮廓索引号)循环查找角点. 对轮廓FMP[index]的链码差计算和链码修复完成后, 再重新对该轮廓循环查找角点, 对链码差分
(1)若
(2)若
(3)若
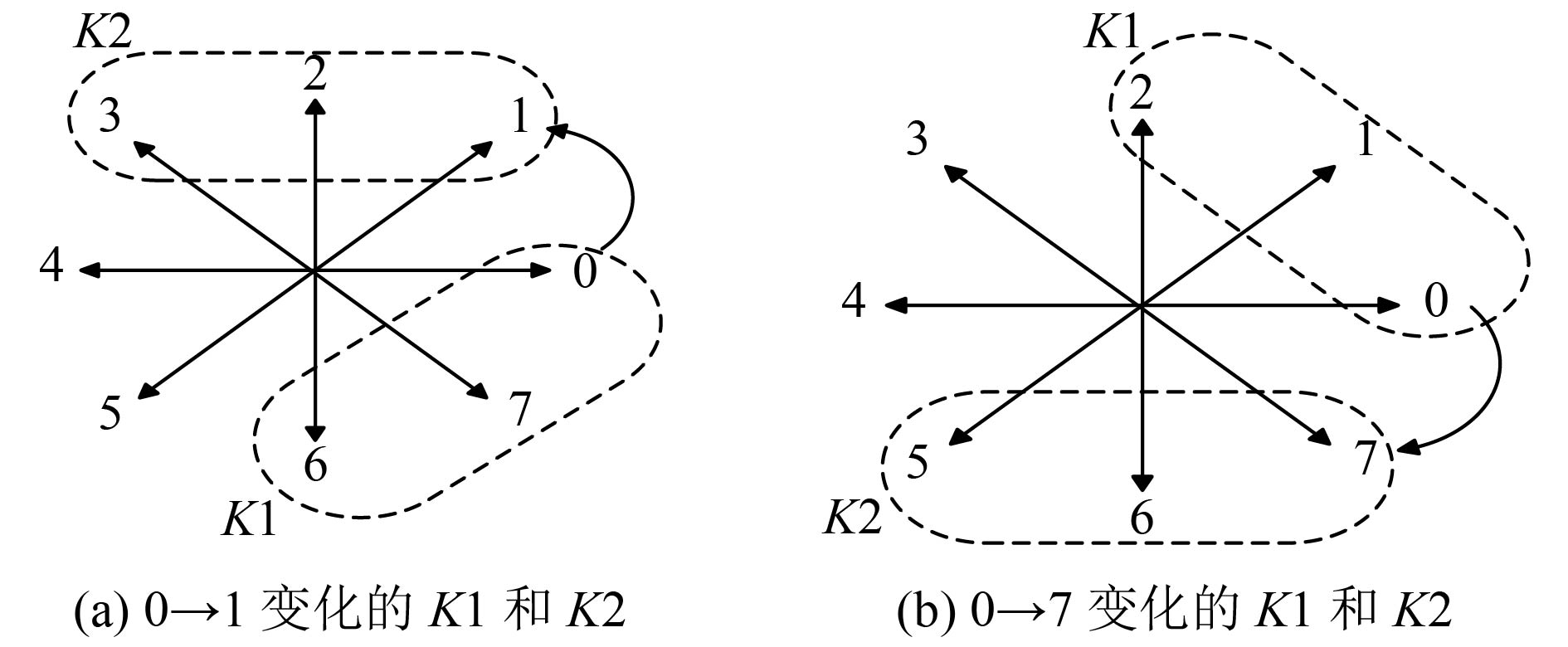
1)当
计算
计算
例如
|
图 5 方向分析示意图 |
2)当
计算
计算
例如
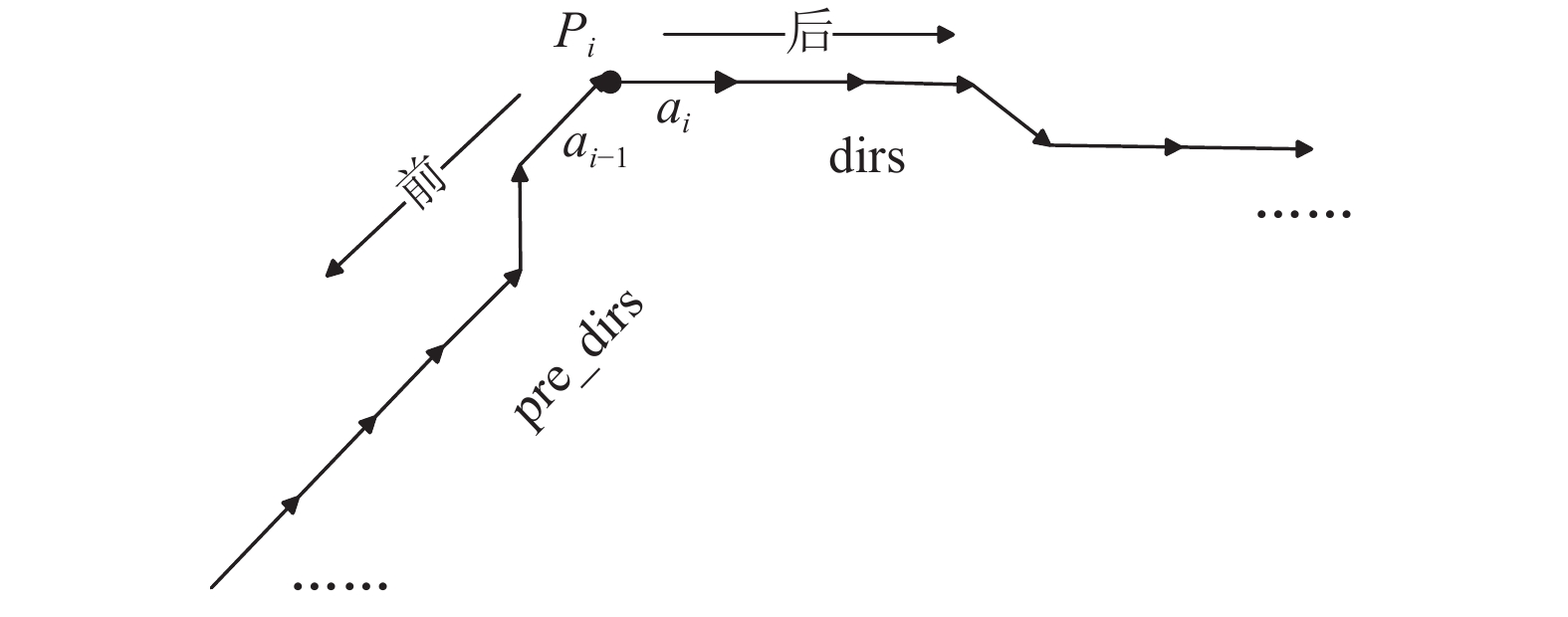
上述得到K1和K2数组后, 再进行如下运算: 对于该点
|
图 6 疑似角点
|
选择执行完上述3种情况后, 角点的判定条件是: Q12==NF, 若满足此条件的点再与vecCorner [index]里的角点比较轮廓差, 若相差小于NF, 则与它最近的角点位置取中间位置作为新角点, 且该点只能比较一次; 若相差大于等于NF, 则直接判定为角点, 存入vecCorner [index].
3.3 算法复杂度分析本文算法在角点检测部分主要是分情况分析链码方向, 对疑似角点的周围几个点的链码值进行分析比较, 不涉及乘除法运算和曲率运算, 算法角点检测部分计算量较少, 计算过程是分轮廓计算, 得到的角点也是分轮廓存储. 本文算法的角点检测部分(不包括轮廓跟踪部分)的时间复杂度为
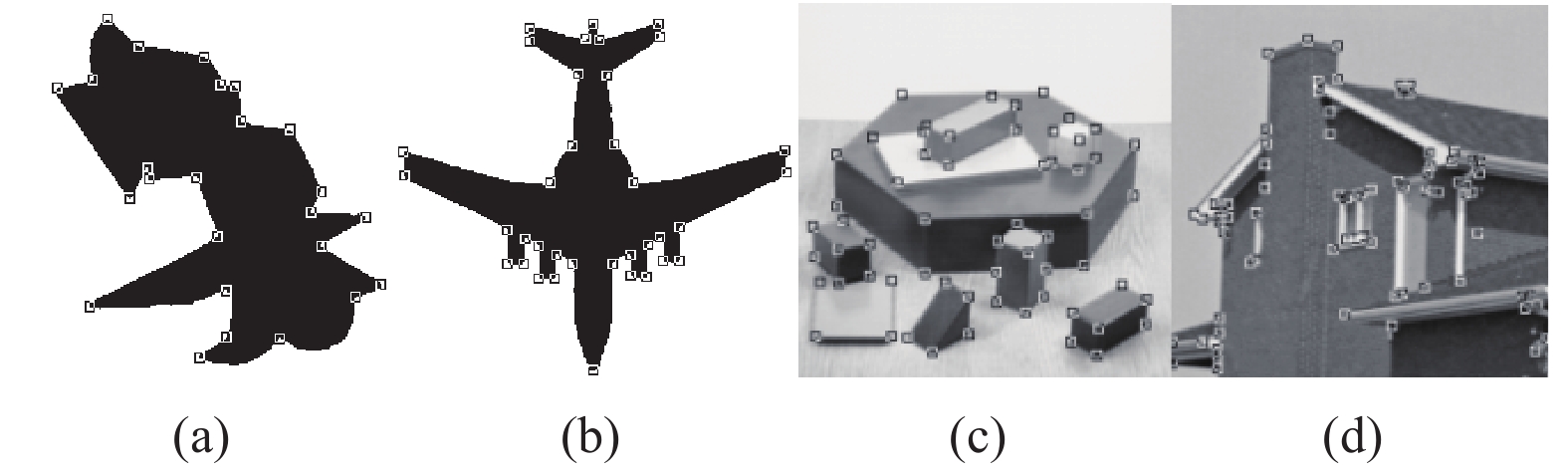
为了验证本文算法的有效性和准确性, 实验在PC(Inter(R) Core(TM) i5-3450 CPU @ 3.10GHz, 8G内存)机上利用MATLAB R2014b进行实验, 与基于边缘轮廓法影响较广且较新的一些算法: ARCSS[14], CPDA[8], Fast-CPDA[9]和He&Yung[7]做比较. 实验所用图和参考图均来自文献[15–18], 如图7所示为角点参考图, 其中两幅二值图, 两幅实物灰度图.
|
图 7 本文实验所用图 |
3.1 准确性实验
本文先以精确度ACU评估五种角点检测算法的准确性[17]. 假设
| $ACU = \frac{{{N_a}}}{2}\left( {\frac{1}{{{N_0}}} + \frac{1}{{{N_t}}}} \right)$ | (2) |
为了对比的公平性, 在比较过程中, 五种算法在提取边缘轮廓选取相同参数, 均采用Canny算法, 低阈值L=0.2, 高阈值H=0.35, 检测时选取算法检测最优结果时的参数[1]进行实验比较. 本文算法参数设置: 相邻因子NF=6, 相同点S=2. 对飞机检测结果如图8, 具体结果如下表1.

|
图 8 各算法对飞机图像的角点检测 |
| 表 1 准确性实验结果 |
由图8和表1可以看出, ARCSS、CPDA和Fast-CPDA检测到的错误角点较少, 但是丢失角点都较多; 虽然He&Yung检测到的角点最多, 但是错误角点也是最多的, 而本文算法检测到的丢失角点与错误角点之和最少, 四幅图的平均准确率也是最高, 可以看出本文算法具有良好的角点检测准确性.
3.2 稳定性实验为了验证算法在图像变换下的鲁棒性, 实验利用图7的四幅基础图建立一个数据集, 经过如下变换[15]:
(1)旋转变换: 旋转角度区间为[–90°,+90°], 每10°旋转一次, 除0°之外;
(2)等比例尺度变换: 尺度因子变化区间为[0.5,2], 以0.1逐步增加, 除1.0之外;
(3)非等比例尺度变换: x的变换范围为[0.7,1.5], y的变换范围为[0.5,1.8], 以0.1逐步增加, 除了都为1.0;
(4)组合变换: 角度旋转区间为[–30°,+30°], 每10°旋转一次, 除0°外; 图像横纵坐标x, y变换范围: [0.8,1.2], 以0.1为单位逐步增加, 其中x, y都为1.0除外;
(5)添加噪声: 噪声范围[0.005,0.05], 以0.005为单位逐步添加零均值高斯白噪声.
图像变换实验时, 以平均重复率(AR)和定位误差(LE)来评价角点检测算法[15]. 假设N0是算法检测初始图像的角点个数, NT是算法检测变换后图像的角点个数,
| ${R_a} = \frac{{{N_r}}}{2}\left( {\frac{1}{{{N_0}}} + \frac{1}{{{N_T}}}} \right)$ | (3) |
平均重复率越高, 说明算法在越稳定. 定位误差为:
| ${L_e} = \sqrt {\frac{1}{{{N_r}}}\sum\limits_{i = 1}^{{N_r}} {\left[ {{{({x_{ti}} - {x_{0i}})}^2} + {{({y_{ti}} - {y_{0i}})}^2}} \right]} } $ | (4) |
其中,
从图9可以看出, 本文算法在除了旋转变换和组合变换下平均重复率不及He&Yung和Fast-CPDA, 其他变换下平均重复率都要高于其他算法; 不过定位误差要高于CPDA、Fast-CPDA和He&Yung算法.最终的平均值如表2.
由表2可以看出, 本文算法在定位误差方面虽然没有CPDA、Fast-CPDA和He&Yung算法好, 但要好于ARCSS, 并且本文算法在5个检测算法具有最高的平均重复率, 说明本文算法具有良好的角点检测稳健性.

|
图 9 5种变换下各算法的AR和LE |
| 表 2 稳定性实验比较结果 |
此外, 本文提出的相邻因子NF和相同点S在图像的等比例尺度变换时可以与尺度因子等比例增减. 实验过程中, 为了实验对比的公平性, 本文没有采用等比例NF和S, 都以不改变NF和S进行角点检测实验. 在实际应用中, 图像执行等比例尺度变换时, 可以采用等比例增减NF和S进行角点检测, 效果更佳.
3.3 算法运行时间实验我们记录上述五种算法运行图7中4幅图所耗费时间, 分别运行10次, 然后计算平均运行时间(除去统一使用的Canny算法运行时间). 运行时间如表3
| 表 3 五种角点检测算法运行时间(单位: s) |
由表3可以得出, He&Yung运行时间最快, 本文算法运行时间稍长于Fast-CPDA、He&Yung和CPDA, 主要在轮廓跟踪得到链码部分耗时较多.
通过以上3种实验对比分析, He&Yung运行时间最快, Fast-CPDA算法定位误差最低, 但本文算法的角点准确率和平均重复率都是最高的, 且本文算法不需要阈值选取.
4 结束语本文提出一种基于Freeman链码方向分析的角点检测算法, 通过巧妙地分析链码方向, 计算链码发生变化时周围多个链码的值是否在一定的数组中来判定角点, 而不需要经过传统的曲线曲率计算检测角点, 同时避免了阈值选取的问题, 实验结果得出本文算法在角点检测时具有良好的检测准确性和稳健性, 角点存储分轮廓具有顺序性, 算法很好理解, 角点检测部分时间复杂度小. 不过在算法前期需要链码的提取, 使得算法运行时间要比He&Yung、Fast-CPDA、CPDA算法稍长, 另外, 本文算法在组合变换中检测角点不够理想, 在以后工作中会加以改进.
| [1] |
Awrangjeb M, Lu GJ, Fraser CS. Performance comparisons of contour-based corner detectors. IEEE Transactions on Image Processing, 2012, 21(9): 4167-4179. DOI:10.1109/TIP.2012.2200493 |
| [2] |
Harris C, Stephens M. A combined corner and edge detector. Proceedings of the 4th Alvey Vision Conference. Manchester, England. 1988. 147–151.
|
| [3] |
洪改艳, 芮廷先, 俞伟广, 等. Harris角点检测的优化算法. 计算机系统应用, 2017, 26(4): 169-172. |
| [4] |
章为川, 孔祥楠, 宋文. 图像的角点检测研究综述. 电子学报, 2015, 43(11): 2315-2321. DOI:10.3969/j.issn.0372-2112.2015.11.026 |
| [5] |
Zhang WC, Shui PL. Contour-based corner detection via angle difference of principal directions of anisotropic Gaussian directional derivatives. Pattern Recognition, 2015, 48(9): 2785-2797. DOI:10.1016/j.patcog.2015.03.021 |
| [6] |
李云红, 姚韵, 贾利娜. 基于图像轮廓的角点检测算法. 计算机与数字工程, 2016, 44(10): 2015-2019. DOI:10.3969/j.issn.1672-9722.2016.10.032 |
| [7] |
He XC, Yung NHC. Corner detector based on global and local curvature properties. Optical Engineering, 2008, 47(5): 057008. DOI:10.1117/1.2931681 |
| [8] |
Awrangjeb M, Lu GJ. Robust image corner detection based on the chord-to-point distance accumulation technique. IEEE Transactions on Multimedia, 2008, 10(6): 1059-1072. DOI:10.1109/TMM.2008.2001384 |
| [9] |
Awrangjeb M, Lu GJ, Fraser CS, et al. A fast corner detector based on the chord-to-point distance accumulation technique. Proceedings of 2009 Digital Image Computing: Techniques and Applications. Melbourne, VIC, Australia. 2009. 519–525.
|
| [10] |
曾接贤, 李炜烨. 曲率尺度空间与链码方向统计的角点检测. 中国图象图形学报, 2014, 19(2): 234-242. |
| [11] |
黄琼丹. 一种基于轮廓分析的图像特征点检测方法. 微计算机信息, 2009, 25(25): 123-125. DOI:10.3969/j.issn.1008-0570.2009.25.051 |
| [12] |
Sonka M, Hlavac V, Boyle R. 图像处理、分析与机器视觉. 兴军亮 艾海舟, 译. 4版. 北京: 清华大学出版社, 2016. 97–106.
|
| [13] |
吴桐树, 张瑞林, 邹敏. 基于Freeman链码的B样条曲线轮廓拟合. 计算机系统应用, 2014, 23(8): 130-134. |
| [14] |
Awrangjeb M, Lu GJ, Murshed M. An affine resilient curvature scale-space corner detector. Proceedings of 2007 IEEE International Conference on Acoustics, Speech and Signal Processing. Honolulu, HI, USA. 2007. I-1233–I-1236.
|
| [15] |
Zhang SZ, Yang D, Huang S, et al. Robust corner detection using the eigenvector-based angle estimator. Journal of Visual Communication and Image Representation, 2017, 45: 181-193. DOI:10.1016/j.jvcir.2017.01.020 |
| [16] |
Xing YX, Zhang DY, Zhao JH, et al. Robust fast corner detector based on filled circle and outer ring mask. IET Image Processing, 2016, 10(4): 314-324. DOI:10.1049/iet-ipr.2014.0952 |
| [17] |
徐玲. 基于图像轮廓的角点检测方法研究[博士学位论文]. 重庆: 重庆大学, 2009.
|
| [18] |
李冬晴. 图像角点检测算法与测评技术研究[硕士学位论文]. 苏州: 苏州大学, 2015.
|
| [19] |
赵亚利, 章为川, 李云红. 图像边缘轮廓自适应阈值的角点检测算法. 中国图象图形学报, 2016, 21(11): 1502-1514. DOI:10.11834/jig.20161110 |
 2018, Vol. 27
2018, Vol. 27



