2. 福建师范大学 医学光电科学与技术教育部重点实验室, 福州 350007;
3. 福建师范大学 福建省先进光电传感与智能信息应用工程技术研究中心, 福州 350007
2. Key Laboratory of Optoelectronic Science and Technology for Medicine of Ministry of Education, Fujian Normal University, Fuzhou 350007, China;
3. Fujian Provincial Engineering Research Center for Optoelectronic Sensors and Intelligent Information, Fujian Normal University, Fuzhou 350007, China
目标跟踪在安防监控、人机交互乃至AI系统中发挥着重要作用. 然而跟踪算法的性能受到了众多问题的限制, 导致如今仍然不存在单一的方法能够同时处理所有问题[1]. 跟踪中算法应对的挑战因素有尺度变化、快速运动、低分辨率等. 近年来较为前沿的目标跟踪算法依据原理主要分为两类: 生成模型和判决模型[2]. 生成式跟踪方法是通过计算机视觉的目标表示方法对目标建模, 搜索与目标外观模型最相似的区域. 增量视觉跟踪算法(Incremental Visual Tracking, IVT)[3]虽然通过少量样本来学习目标的外观模型, 但遇到遮挡因素就会影响目标的外观. 基于多任务稀疏学习的鲁棒性目标跟踪算法(Robust Visual Tracking via Multi-Task Sparse Learning, MTT)[4]利用APG原理保证快速收敛, 提高了跟踪速度, 但跟踪精度不高. 分布式跟踪场(Distribution Fields for Tracking, DFT)[5]算法在目标表示中引入模糊性, 克服了形变和光照变化的影响, 但跟踪速度有待提高. 生成式方法所带的信息丰富, 但不能充分地利用背景信息, 鲁棒性不高. 而且由于其复杂外观模型, 跟踪非常耗时. 判别式跟踪算法则将跟踪问题看作一个二分类问题, 对分类器进行训练, 将目标与背景进行分离. 与上述生成式方法相比, 其能充分利用目标和背景信息, 准确率更高, 但不能反映自身特性. 比较主流算法有基于核化的结构化输出(Structured Output Tracking with Kernel, Struck)[6]算法、压缩感知(Compressive Tracking, CT)[7]算法等, 这些算法为了实时跟踪, 通常选取的样本有限. 而基于相关滤波器的目标跟踪算法由于高效率、高精度引起关注. 例如, Henriques等人提出循环结构跟踪器(Circulant Structure of Tracking, CSK)[8]通过循环移位进行稠密采样, 获得目标包含的信息, 并且在检测过程中采用循环移位构造大量候选图像块, 然后结合快速傅立叶变换进行分类器训练. Danelljan等[9]在CSK基础上引入了颜色属性特征, 为了提高效率, 对特征向量采用降维技术. 后来, 核相关滤波目标跟踪算法(Kernelized Correlation Filters, KCF)[10]被提出, 它是利用多通道的HOG特征来替代了单通灰度特征, 并且使用核函数的方式对多通道HOG特征进行融合, 加强分类器鲁棒性, 但在目标运动模糊或背景受噪声干扰严重时, HOG的描述能力就变弱. 而以上基于相关滤波器算法难以对目标运动中发生的较大尺度变化进行有效的处理, 这会使得分类器模型出现误差累积, 最终会导致跟踪精度降低. 于是, 本文在KCF基础上融入颜色特征, 可与HOG特征组成更鲁棒的特征; 加入了尺度检测, 在后续帧中对当前目标建立尺度模型, 通过检测与上一帧尺度模型进行相关滤波响应值的位置, 计算目标的尺度; 另外, 加入重检测模块, 对目标的置信度进行判定, 减少与目标外观模型的偏差.
2 KCF跟踪算法KCF算法虽然用HOG特征代替了灰度特征, 增强了对光照变化的适应性, 但仅靠这一个特征很难对复杂场景变化进行处理. 由于KCF算法使用大小恒定的跟踪框, 当目标尺度发生变化时, 算法的跟踪准确度会降低. 从本质上来说, 这其实是一种模板匹配的方法, 第一帧图像初始化对后续的跟踪是有影响的. 此外, 由于周期性循环移位产生的边界效应, 算法不能有效地处理遮挡问题.
针对以上问题, 本文对KCF方法进行改进:
(1) 融合了颜色属性特征. 该特征和图像中场景物体十分相关, 并且计算简单. HOG特征强调图像的梯度, 而颜色特征是全局特征, 不能很好捕捉对象的局部特征, 将此两种特征进行融合来创建更强的特征集.
(2)引入了尺度估计, 解决了模板固定问题, 实现尺度自适应.
(3)然而KCF算法仍然会因为目标所处的环境因素使得跟踪结果失败, 例如: 目标受到物体遮挡、遇到与目标相似的物体等等. 因此本文为了能够长期跟踪目标, 加入了再定位的组件.
2.1 分类器训练对于判别式跟踪算法主要分为训练和检测两个步骤. 对于训练图像, 我们可以看作岭回归问题. 这是由于岭回归对任意的输入有闭式最优解. 训练的目标是找到一个函数
| $\mathop {\min }\limits_w \sum\limits_{m,n} {({f}({{x}_{m,n}}} ) - {{y}_{m,n}}{)^2} + \lambda ||{w}|{|^2}$ | (1) |
根据文献[11]可求得闭式解:
| ${w} = {({{X}^{{ H}}}{X} + {\lambda I})^{ - 1}}{{X}^{ {H}}}{Y}$ | (2) |
其中X为样本矩阵, Y为回归目标. 当f(x)为非线性时, 可将x映射到高维空间
| ${w} = \sum\limits_{{{m,n}}} {{\alpha _{{{m,n}}}}} \varphi ({{x}_{{{m,n}}}})$ | (3) |
此时需要优化的变量是
| ${\varphi ^{{T}}}({x})\varphi ({x}') = {K}\left( {{x},{x}'} \right)$ | (4) |
可以解决高维特征矩阵点积计算复杂问题. 由文献[12]可求解:
| $\alpha = {({K} + \lambda {I})^{ - 1}}{y}$ | (5) |
其中
检测样本则取下一帧中同样位置的图像块
| ${z_i} = {{p}^{{i}}}z$ | (6) |
对于待检测的图像块, 响应可表示为:
| ${y} = \sum\limits_{{i}} {{{a}_{{i}}}{k}({{x}_{{i}}}} ,z)$ | (7) |
利用循环矩阵性质
KCF算法采用HOG, 虽然HOG特征具有一定的平移、旋转不变性和光照不变性, 但这种单一的特征难以适应跟踪中出现的多种挑战因素. 而CN特征[13]具有对图像大小和方向不敏感的特点. 所以改进算法将HOG和CN两种特征进行融合, 然后对目标进行描述, 可实现优势互补, 提高了分类器的性能. 假设两个特征向量为
| ${\varphi ^{{T}}}({x})\varphi ({x}') = {K}\left( {{x}},{{x}}' \right)$ | (8) |
然后通过高斯核函数, 将方向梯度直方图(HOG)和CN特征级联组合成特征集, 以此构建更强力的目标外观.
3.2 尺度估计由于目标会发生尺度和旋转等变化, 如果不能自适应尺度的变化, 更新模型过程中会出现误差累积, 导致跟踪不准确或者跟踪失败. 因此对目标的尺度进行抽样[14], 得到尺度空间. 用P×Q表示当前帧目标的尺度大小, N为尺度样本数, 尺度的取值范围用集合
| $\hat s = \mathop {{{argmax}}}\limits_s ({{max}}({\hat y_1}),{{max}}({\hat y_2}),\cdots,{{max}}({\hat y_s}))$ | (9) |
其中
与之前的长期跟踪方法TLD相比, 不同之处在于再检测机制并没有每帧都进行更新, 采用阈值方法. 为了提高计算效率, 若检测后得到的值小于阈值T1, 则检测器开始重新检测跟踪目标, 这时我们利用随机蕨分类器对当前帧进行扫描, 最后再评估目标的置信度信息. 若检测后的最大值比阈值T2大, 则获取正负样本并利用它们来训练和更新分类器. 对于待检测的图像块而言, 我们使用最近邻分类器(Nearest Neighbor Classifier)的相似度度量方式. 在跟踪过程中, 图像块与目标框的重叠率大于0.7的作为正样本, 重叠率小于0.2的作为负样本. 这里的阈值是根据经验设定的.
3.4 改进的算法步骤1) 读入视频序列帧, 在第一帧图像中对目标进行初始化, 确定搜索区域与目标区域.
2) 提取目标特征, 对位置滤波模板和尺度滤波模板进行训练.
3) 位置检测: 在下一帧中, 根据上一帧所确定的位置与尺度, 选择一定尺寸的搜索区域, 插值到与位置滤波器一样的尺寸, 提取特征, 计算响应值, 得到新位置.
4) 尺度检测: 在目标位置附近创建尺度金字塔, 根据尺度调整图片大小, 利用分类器对样本的最高得分来更新目标的位置.
5) 再检测: 如果检测的最大值小于重检测阈值T1, 启动分类器重新扫描, 找到候选的位置, 计算置信度. 最大的值所在的位置即为目标.
6) 如果检测的最大值大于目标外观阈值T2时, 训练并更新分类器.
4 实验结果与分析为验证本文提出的算法是否对目标的尺度变化和遮挡等问题有所改善, 本文算法对OTB-2013的50个含有不同属性的视频进行评估, 属性分别为光照变化(Illumination Variation, IV)、尺度变化(Scale Variation, SV)、遮挡(Occlusion, OCC)、运动模糊(Motion Blur, MB)、快速运动(Fast Motion, FM)、平面外旋转(Out-of-Plane Rotation, OPR)、平面内旋转(In-Plane Rotation, IPR)和复杂背景(Background Clutters, BC)[15].
4.1 实验环境与参数本文使用Window 7操作系统, 计算机CPU为Intel Xeon处理器, 主频3.0 GHz, 内存4 GB, 实验软件平台为MATLAB 2012a. 实验中HOG特征的cell大小为4, 梯度方向个数为9, 正则项参数λ为0.01, 学习参数η为0.015, 尺度样本数为33, 尺度因子为1.02, T1为0.5, T2为0.6.
4.2 定性分析(1) 遮挡和旋转
在图 1中, 视频jogging中跑步的人受到电线杆的遮挡, 只有本文的算法和TLD的算法在受到遮挡后仍能对目标进行跟踪, 其它的算法已经丢失了跟踪框. 这是由于本文的算法加入了再检测的机制, 可以提高对目标的定位能力, 而KCF则跟踪失败. 图 2这个tiger2视频序列除了遮挡因素外还伴有强烈光照变化和旋转等挑战因素, 旋转会使目标纹理受到影响, 尤其是在受到长时间遮挡后, 模板没有及时更新情况下, 即使目标离开再重回视野也难以继续跟踪. 到289帧时, 只有本文算法能跟踪准确. 而KCF算法由于没有再检测模块, 无法重新定位目标的位置.
| 表 1 实验测试的视频属性 |

|
图 1 jogging |

|
图 2 tiger2 |
(2) 快速运动和运动模糊
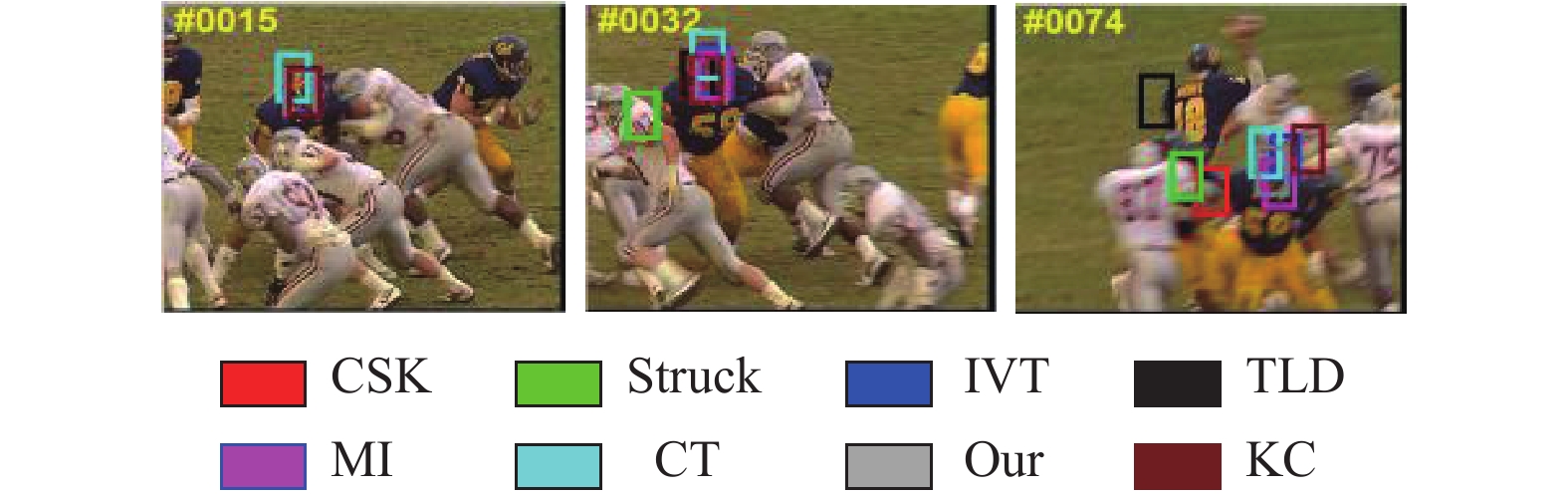
图 3 jumping中人一直快速运动, 到第106帧时KCF跟踪框开始出现丢失现象, 这是由于目标的快速运动导致外观发生了大幅变化. 到312帧时仅剩下struck、TLD、MIL和本文算法能继续跟踪. 这是由于本文算法加入了对置信度的判定, 减少与模型的误差累积. 图 4 deer序列在第24帧时出现运动模糊, 会导致特征判别能力减弱, 在52帧时受到周围相似鹿干扰, 除了本文的算法能跟踪到正确位置, 其他算法的目标框与真实位置出现误差. 图 5 football1序列在第74帧时可以发现KCF跟踪算法受旋转和复杂背景挑战因素影跟踪失败, 而本文算法能准确跟踪, 这是由于特征的融合提高了目标外观模型的鲁棒性.
(3) 尺度变化
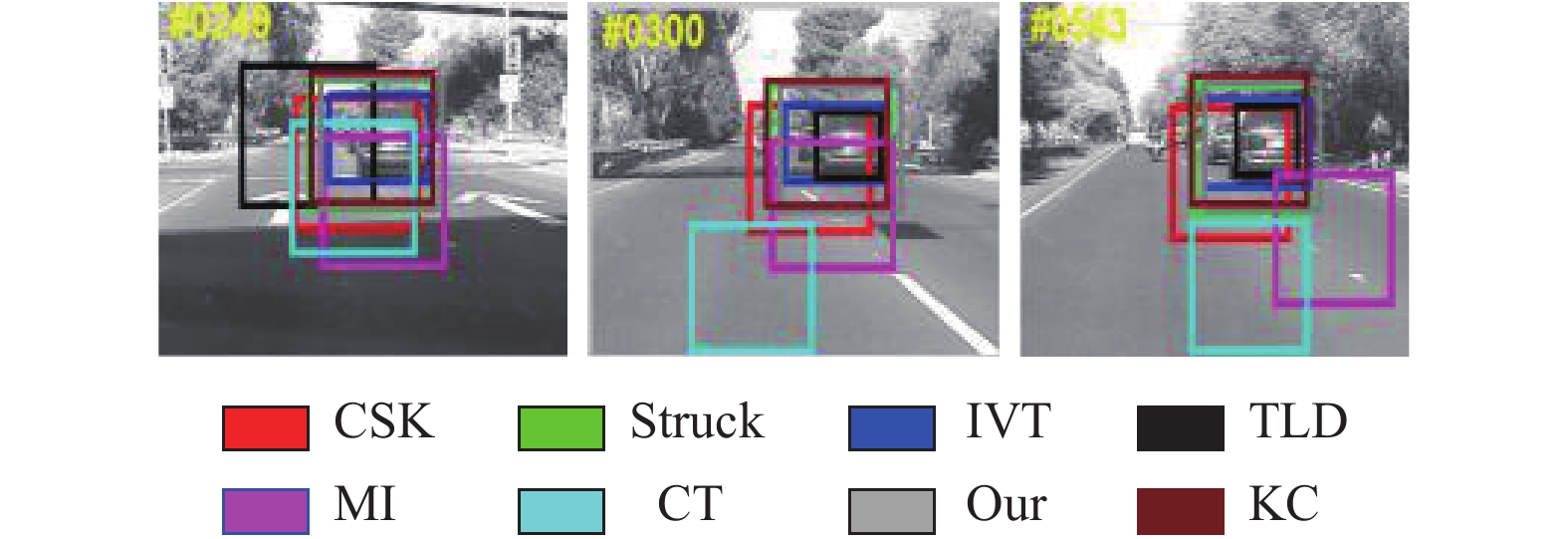
图 6 car4数据集中, 车尺度从大变小, 又伴随着光照影响, TLD、IVT和本文算法均可较好地处理尺度变化. 本文算法相较于KCF跟踪较准确原因在于当位置滤波器能准确跟踪到目标中心后, 引入的尺度估计会搜索最为匹配的尺度, 可以更好适应目标外观变化.

|
图 3 jumping |

|
图 4 deer |
|
图 5 football1 |
|
图 6 car4 |
4.3 定量分析
通过选取10个富有挑战性视频, 利用中心位置误差和重叠精度来衡量改进算法与KCF算法. 中心位置误差是指对图像人工标定的目标位置与跟踪到位置之间的欧氏距离. 重叠精度指跟踪的目标框区域与真实目标框区域的交集占并集的比例. 由表2和表3可见, 改进算法相对KCF算法有较鲁棒性的跟踪结果. 改进的算法中心位置误差的均值相比于KCF算法提高10%. 对于重叠率, 改进算法较于KCF算法则提高了15%. 这是由于改进算法能实现自适应尺度跟踪, 它是在当前目标的不同尺度之间去寻找一个最优值, 而且再检测机制又提高了目标的定位能力.
| 表 2 改进算法与KCF算法中心位置误差的对比(单位: pixel) |
| 表 3 改进算法与KCF算法重叠率对比(单位: %) |
4.4 整体性能评估
本文采取跟踪成功曲线图来评估目标跟踪方法的性能, 反映的是跟踪结果与数据真实值之间重合部分面积的比例. 随着重叠阈值的增大, 其成功率反而减小. 当重叠率大于0.5时, 一般认为跟踪成功. 为了客观地评价算法性能, 利用成功率曲线下的面积作为性能的评价准则. 曲线下的面积越大, 则跟踪器性能越好. 通过在OTB-2013数据集上与原有算法进行

|
图 7 本文算法(cqgz)与其他算法在几种属性上的成功率与精度的比较 |
对比测试, 由图7可以看出, 改进的算法的成功率在尺度变化、运动模糊、变形和低分辨率情况下分别高出了9%、6%、4%和13%. 由于跟踪过程中可以对目标过程中出现的尺度变化进行相应处理, 另外, 再检测模块使得物体受到遮挡后重回视野, 可以重新定位目标的位置. 从定性分析、定量分析以及整体性能评估中可以看出, 改进的算法较于其他跟踪器来说相对较好.
5 结论与展望通过核函数将HOG特征和颜色特征进行融合, 可以提高抗遮挡能力. 针对基于核相关滤波器的算法不能对尺度变化有较好的适应性, 本文构建尺度相关滤波器, 可实现多尺度自适应地对目标进行跟踪, 实时更新尺度模型. 最后加入再检测模块, 训练在线分类器, 提高正样本的准确性. 当目标丢失后重回场景, 可锁定目标继续跟踪. 测试结果表明, 所提的算法对尺度、运动模糊等问题能进行有效地处理, 在复杂背景下跟踪性能较优, 但仍存在不足. 未来可考虑两点: (1)利用深度学习, 将卷积神经网络中不同特征图结合, 然后在相关滤波框架下进行跟踪; (2)对尺度估计方法改进或对特征进行并行计算, 以提高算法速度.
| [1] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
| [2] |
Smeulders AWM, Chu DM, Cucchiara R, et al. Visual tracking: An experimental survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1442-1468. DOI:10.1109/TPAMI.2013.230 |
| [3] |
Ross DA, Lim J, Lin RS, et al. Incremental learning for robust visual tracking. International Journal of Computer Vision, 2008, 77(1–3): 125-141. |
| [4] |
Zhang TZ, Ghanem B, Liu S, et al. Robust visual tracking via multi-task sparse learning. Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, USA. 2012. 2042–2049.
|
| [5] |
Sevilla-Lara L, Learned-Miller E. Distribution fields for tracking. Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, USA. 2012. 1910–1917.
|
| [6] |
Hare S, Saffari A, Torr PHS. Struck: Structured output tracking with kernels. Proceedings of 2011 IEEE International Conference on Computer Vision (ICCV). Barcelona, Spain. 2011. 263–270.
|
| [7] |
Zhang KH, Zhang L, Yang MH. Real-time compressive tracking. Proceedings of the 12th European Conference on Computer Vision. Florence, Italy. 2012. 864–877.
|
| [8] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence, Italy. 2012. 702–715.
|
| [9] |
Danelljan M, Khan FS, Felsberg M, et al. Adaptive color attributes for real-time visual tracking. Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Columbus, OH, USA. 2014. 1090–1097.
|
| [10] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [11] |
Gray RM. Toeplitz and circulant matrices: A review. Foundations and Trends® in Communications and Information Theory
, 2005, 2(3): 155-239. DOI:10.1561/0100000006 |
| [12] |
Rifkin R, Yeo G, Poggio T. Regularized least-squares classification. In: Suykens J, Horvath G, Basu S, et al. eds. Advances in Learning Theory: Methods, Models and Applications. Amsterdam: IOS Press, 2003. 131–154.
|
| [13] |
van de Weijer J, Schmid C, Verbeek J, et al. Learning color names for real-world applications. IEEE Transactions on Image Processing, 2009, 18(7): 1512-1523. DOI:10.1109/TIP.2009.2019809 |
| [14] |
Danelljan M, Häger G, Khan FS, et al. Accurate scale estimation for robust visual tracking. Proceedings of British Machine Vision Conference 2014. Nottingham, UK. 2014.
|
| [15] |
Wu Y, Lim J, Yang MH. Online object tracking: A benchmark. Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Portland, OR, USA. 2013. 2411–2418.
|
 2018, Vol. 27
2018, Vol. 27



