锡林河流域属于典型性草原型流域, 地处内蒙古高原中部, 流域总面积约为10 800 km2. 是锡林郭勒草原上的主要河流, 因此对它展开研究具有重要的意义[1]. IPCC第四次评估报告指出, 近50年来全球地表增温速度明显加快, 若气候变化超出生态系统的弹性阈值, 将严重破坏生态系统的结构和功能, 后果不堪设想[2]. 而气象站的设定可以获得有关气候变化的气象数据. 但是气象数据是以时间序列而采集, 通常以分钟为单位, 采集的密度浓且指标多. 随着时间的累积将获得大量监测的气象数据, 增加了数据的复杂性. 而数据融合技术则是大数据处理中处理数据的一种方式. 通常的数据融合算法针对多个传感器在同一时间不同空间的特征数据的融合. 而在实际应用中, 一个气象站节点上不止一类传感器, 况且每种传感器都用有自己的特性, 例如温度传感器所采集的温度变化缓慢, 如果按照固定的采样频率, 将会产生大量的重复冗余的数据, 并增加网络的传输量, 所以数据融合的研究成为人们关注的焦点[3]. 例如, 刘卫萍等人将数据融合技术应用于环境测量中, 对多传感器监测的环境数据进行转换、相关性分析、融合, 降低数据的规模[4]. 张鹏鹏等对矿井安全监测数据实施融合, 提高数据采集的准确性[5].
数据融合是充分利用不同时间与空间的多传感器数据资源, 采用计算机技术按时间序列获得传感器的观测数据, 在一定准则下进行分析. 当前, 主要的数据融合方法有加权平均、卡尔曼滤波法、贝叶斯估计法、证据推理等. 其中贝叶斯估计法和证据推理是在静态环境适用于高层的数据融合; 加权平均和卡尔曼滤波法适用于动态环境的低层数据的融合. 卡尔曼滤波是目前应用最广泛的滤波方法. 刘超云等人提出卡尔曼滤波算法对多个滑坡体位移监测数据进行滤波融合, 从而对其稳定状态和变化趋势做出预测[6]. 邹波等人提出基于EKF的改进非线性定姿估计方法, 通过多传感器互补, 利用仪器的进行误差修正, 得到准确的姿态角[7]. Ou等人通过多传感器互补, 采用连续EKF进行姿态估计, 提高姿态角估计的动态和稳态性能[8]. 龙慧提出基于Consensus滤波的分布式卡尔曼融合算法, 引入一致滤波算法用于计算节点平均观测数据和平均你协方差, 从而获得各节点的分布式状态估计[9]. Subhro等人提出一种单一时间尺度的分布式卡尔曼滤波算法, 获得不稳定系统的有节MSE的无偏估计[10]. Lvanjko等通过采用扩展卡尔曼滤波和无迹卡尔曼滤波的融合实现移动机器人姿态的跟踪[11]. 吴勇等提出一种收缩无迹卡尔曼滤波器, 并应用于SLAM问题中, 通过设置收缩参数降低计算复杂度[12].
卡尔曼滤波是线性无偏最小方差估计, EKF是将非线性系统线性化, 然后进行卡尔曼滤波, 但是线性化处理时需要用雅克比矩阵, 其繁琐的计算过程导致该方法实现相对困难. UKF是针对非线性系统, 但是计算量大. 与EKF相比较, 它有更高的估计精度和更强的鲁棒性及稳定性, 但当周围环境发生较大变化, 其精度和稳定性都会大大降低[13].
已提出的各种不同卡尔曼滤波算法, 在融合的精度上和计算的复杂性有所提高, 但是都是针对不同空间的多个传感器的数据融合算法, 属于横向融合. 而实际采集的气象数据仅来源于相距较远的两个气象站, 采集数据密度密, 所以将上述算法应用于纵向基于时间序列数据的融合, 计算复杂性相对高. 因此, 本文将卡尔曼滤波算法应用于纵向基于时间序列数据的融合. 因此本文以典型草原流域锡林河流域为研究对象, 引入分布图法, 利用传统的卡尔曼滤波算法对气象数据中变化缓慢的空气温度指标进行同一空间不同时间序列的融合, 以减少数据的传输量, 提高数据的准确性与科学性, 同时方便以后的计算. 通常探测数据采用平均值作为瞬时值, 如果测量的数据出现不完整性或者存在异常, 将会导致最终结果的不准确. 所以处理异常或者缺失数据进行融合将是本研究的重点.
1 融合算法 1.1 卡尔曼滤波算法卡尔曼滤波算法采用递归方法来解决线性滤波问题, 主要用于动态环境中冗余信息的融合, 根据上一状态的估计值和当前状态的观测值推出当前状态的估计的滤波方法[14,15]. 首先引入一个离散控制过程的系统和系统的测量值, 用公式(1)和(2)描述:
| ${X_k} = A{X_{k - 1}} + B{U_k} + {W_k}$ | (1) |
| ${Z_k} = H{X_k} + {V_k}$ | (2) |
其中, Xk是k时刻对系统状态变量, Uk是k时刻对系统的控制量, A和B是系统的参数, Zk是k时刻的测量值, H为测量系统的参数, Wk和Vk是过程和测量噪声, 假设其均为高斯白噪声, 噪声协方差分别用q, r表示.
由公式(1)和(2), 可得出卡尔曼滤波器的时间更新方程, 包含时间递推状态变量计算和向前推算误差协方差的计算:
| ${\hat X_{k,k - 1}} = A{\hat X_{k - 1}} + B{U_k}$ | (3) |
| ${P_{k,k - 1}} = A{P_{k - 1}}A' + Q$ | (4) |
基于现在时刻的观测值和前一时刻的估计值, 可得卡尔曼滤波器的状态更新方程, 包含观测量的更新估计、卡尔曼增益计算和更新误差协方差:
| ${\hat X_k} = {\hat X_{k,k - 1}} + K{g_k}\left( {{Z_k} - H{{\hat X}_{k,k - 1}}} \right)$ | (5) |
| $K{g_k} = {P_{k,k - 1}}H'/\left( {H{P_{k,k - 1}}H' + R} \right)$ | (6) |
| ${P_k} = \left( {1 - K{g_k}H} \right){P_{k,k - 1}}$ | (7) |
其中,
卡尔曼滤波算法通过不断的预测和校正获得最终的准确的测量值.
1.2 卡尔曼滤波的参数设置在实际滤波时, 需要根据测量数据的实际情况设置初值X0, 初始误差协方差P0(P0≠0), 过程噪声协方差Q, 和测量噪声协方差R, 使得滤波收敛速度和效果最佳. 由于卡尔曼滤波算法是一个最优化自回归的算法, 所以X0可以取0或者测量的初始值. 通常P0越小表示初始的估计较好. 如果测量的环境相对稳定, Q可设置为一个确定的值, Q的取值越接近0, 融合的曲线越光滑, 但不宜特别小. R与测量仪器的精度有关, R取值与Q相类似, R越小, 滤波效果好, 收敛快[16].
1.3 改进的卡尔曼滤波算法 1.3.1 分布图法对于一个相对稳定的环境, 传统的卡尔曼滤波算法可以获得较好的融合结果. 当是当数据出现异常或者缺失, 传统的卡尔曼滤波算法的融合结果将会出现波动. 针对该问题, 对传统的卡尔曼滤波算法实施改进, 引入了分布图法[17], 对测量数据进行处理, 在利用卡尔曼滤波算法融合, 得到可靠的融合结果. 分布图法通过计算判断区间[ρ1, ρ2]来排除50%的离异值干扰. 而且中位值和四分位离散度的选择与极值点的大小无关, 仅取决于数据的分布位置, 有效区间的获得与疏失数据的关系不大, 而且利用分布图法获得的数据不受数据分布的限制[18]. 所以分布图法消除疏失数据具有运算量小、鲁棒性强、实时性好的优点[19]. 为了保证数据的维数不变, 将采用估计值来代替疏失数据, 这样可以减少维数的判断, 提高计算的效率.
首先引入分布图法的参数, 将测量的气象温度数据按从小到大的顺序排列, 设为T1, T2, …, TN, 则中位数Tm按公式(8)的定义, 中位数将数据序列分为上四分位FU和下四分位FL, 四分位离散度dF为FU和FL的差值. 如果气象温度数据与中位数的距离大于βdF, 则称该数据为无效数据, β为常数.
| ${T_M} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle{T_{\frac{{N + 1}}{2}}},\;\;\;\;\;\;\;\;\;\;\;\;\;N \text{为奇数}}\\{\frac{{{T_{\frac{N}{2} + 1}} + {T_{\frac{N}{2}}}}}{2},\;\;\;\;\;N \text{为偶数}}\end{array}} \right.$ | (8) |
假设有效数据的判断区间为[ρ1, ρ2], 则不包含在这个区间内的数据认为异常数据. 其中,
| ${\rho _1} = F{}_L - \frac{\beta }{2}dF\;,\;{\rho _2} = {F_U} + \frac{\beta }{2}dF$ | (9) |
当判断出异常数据, 为了使得数据维数保持一致, 则通过对中间温度数据求平均值, 来代替当前时刻的估计值, 如表1.
| 表 1 中间数据的平均值计算 |
1.3.2 算法步骤
改进的卡尔曼滤波算法的具体步骤如下:
1)读入融合的测量数据, 并对数据进行排序, 利用分布图法确定异常或疏失数据, 并用平均值来代替测量数据中的异常数据;
2)初始化卡尔曼滤波算法的参数, 包括参数A, B, H, 以及P0和X0的初始值, 并计算过程和测量的噪声的协方差q, r;
3)利用卡尔曼滤波算法中的公式, 通过循环迭代计算, 对测量数据实施融合.
2 实验及结果分析选取锡林河流域内石门景区气象站2016年1月1日每隔5分钟所采集的空气温度数据, 所以1小时之内可以采集到12个空气温室数据, 24小时, 共288个采用数据, 部分数据如表2所示, 利用改进的卡尔曼滤波算法按照小时对数据实施融合, 将融合为12个数据.
由于空气温度传感器采集过程相对稳定, 且采集的数据与温度是直接对应的, 所以采用一维线性的离散系统, 将变量A和H均设置为1. 噪声的来源主要源于环境和采集仪器, 所以Wk和Vk且均为零均值的独立的高斯白噪声, 方差分别为q=0.04和r=0.2.
1)原始数据的融合
表2中的空气温度数据如图1所示. 可以明显的看出一天温度变化趋势, 中午两点空气温度已经达到了极值, 将其使用平均值、卡尔曼滤波和改进的卡尔曼滤波融合后的结果如图1(b)所示.
从图1结果对比中可以看出, 三种方法的融合趋势大致相同. 在上午6点, 卡尔曼滤波算法的融合值存在微小的突变; 凌晨2点到3点, 平均值算法的融合结果也存在突变, 所以与平均值算法和卡尔曼滤波算法相比, 改进的卡尔曼滤波算法的融合曲线更光滑, 符合空气温度的缓慢变化规律
| 表 2 空气温度采样数据(单位: °C) |
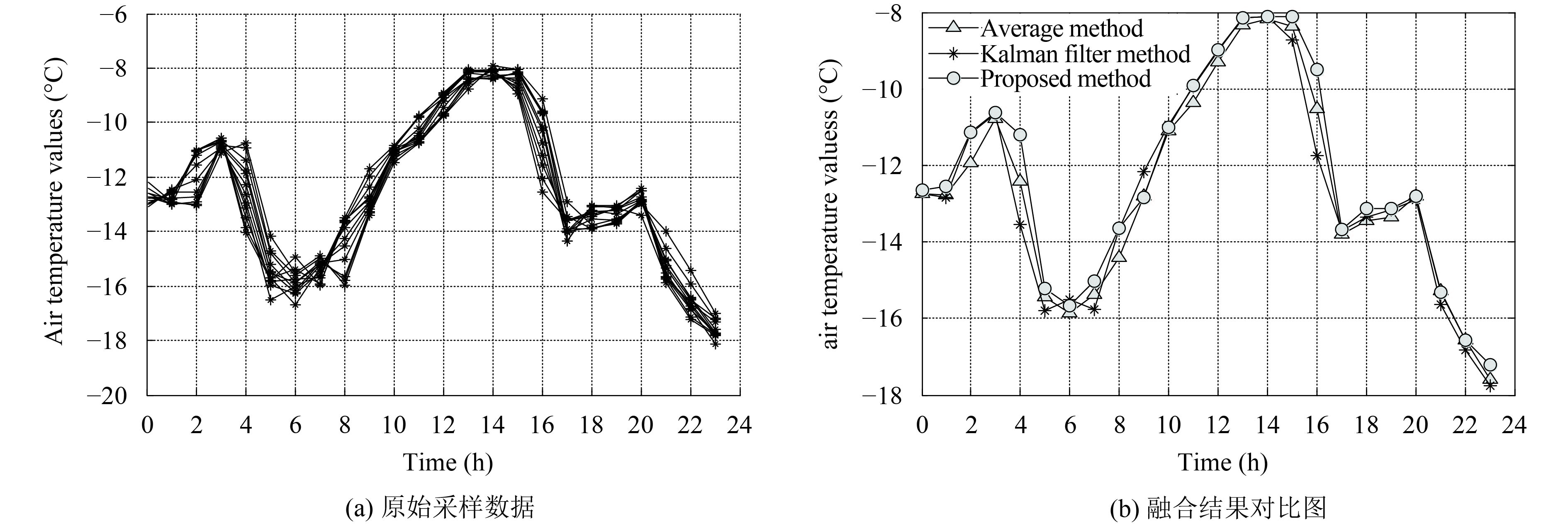
|
图 1 原始数据及融合结果 |
2)添加扰动数据和突变数据
为了验证改进的算法的性能, 在原始的空气数据中设置了四个扰动数据和两个突变数据, 其中突变数据是将原始数据设置为最大或者是0, 0点和9点设置减小的扰动数据, 13点和22点设置增大的扰动数据. 设置的位置如表3所示.
| 表 3 添加的扰动和突变的数据(℃) |
由于设置了6个疏失数据, 利用分布图法判断该数据, 并赋予估计值, 如表4所示.
从表中可知, 估计值与原始数据值相差较小, 误差介于–0.4~0.28.
| 表 4 疏失数据的估计值(℃) |
对扰动数据和突变数据分别用平均值、卡尔曼滤波和改进的卡尔波滤波算法融合, 其融合结果显示在图2中, 相应的改变的值显示在表5和表6中.
依据图2(a)和表5可知, 在0点设置的扰动数据, 平均值法融合结果显然从–12.74℃下降到–13.76℃, 不能避免扰动数据的干扰. 卡尔曼滤波算法的融合结果仅在–0.33到0.02的小范围内波动. 而改进的算法的融合结果的波动范围更小, 为–0.1到0.09. 同时, 与卡尔曼滤波算法, 改进方法的融合结果与设置扰动数据的增减性一致. 因此, 改进的算法不受扰动数据的影响.

|
图 2 设置异常数据的融合结果 |
| 表 5 三种方法对扰动数据的融合结果对比(℃) |
| 表 6 三种方法对突变数据的融合结果对比(℃) |
从图2(b)和表6可知, 平均值法对突变数据的融合结果影响大于其他两种方法的融合结果. 对于改进的融合算法在16点时, 添加突变数据和原始数据的融合结果是一样的, 是由于改进的融合算法将突变数据剔除, 用表1中计算的平均值代替突变数据. 因此改进的方法能避免突变数据. 综上所述, 利用分布图法判断疏失数据, 并用估计值来代替疏失数据, 在利用卡尔曼滤波算法进行融合, 能够获得光滑的融合结果, 具有较强的稳定性、健壮性.
对于时间跨度比较的大的温度数据, 可以利用本文的算法对数据进行融合, 从而了解温度的变化趋势. 选择2016年1月1日到10日的数据, 每隔五分钟采集, 则共有2880条记录. 按小时融合后的数据共240条, 显示在图3中; 按天进行融合的数据共10条, 如图4所示. 从中可以清楚的看到, 温度在1月6日和1月7日出现极值点, 且1月7日的温度最低.
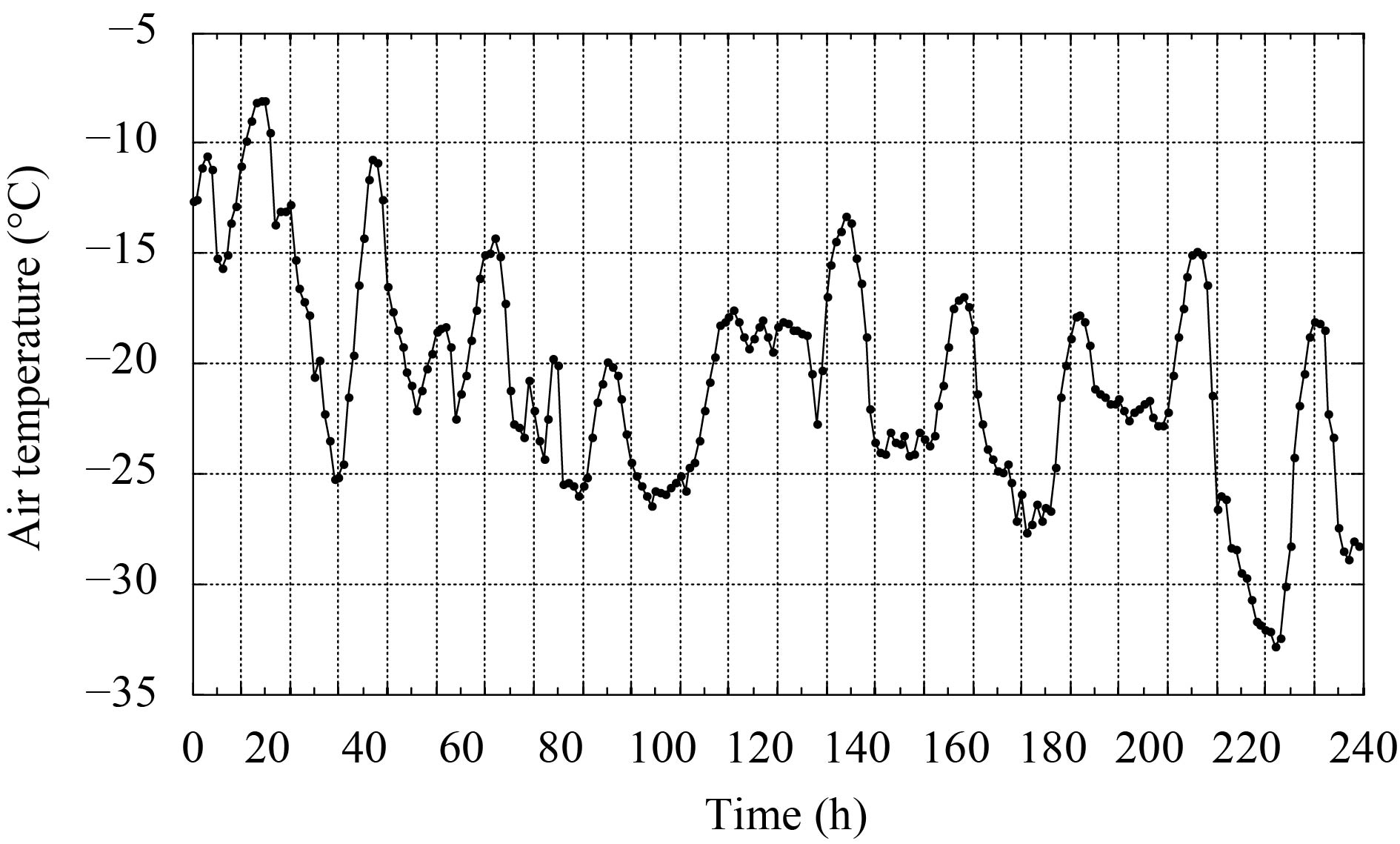
|
图 3 按小时的融合结果 |
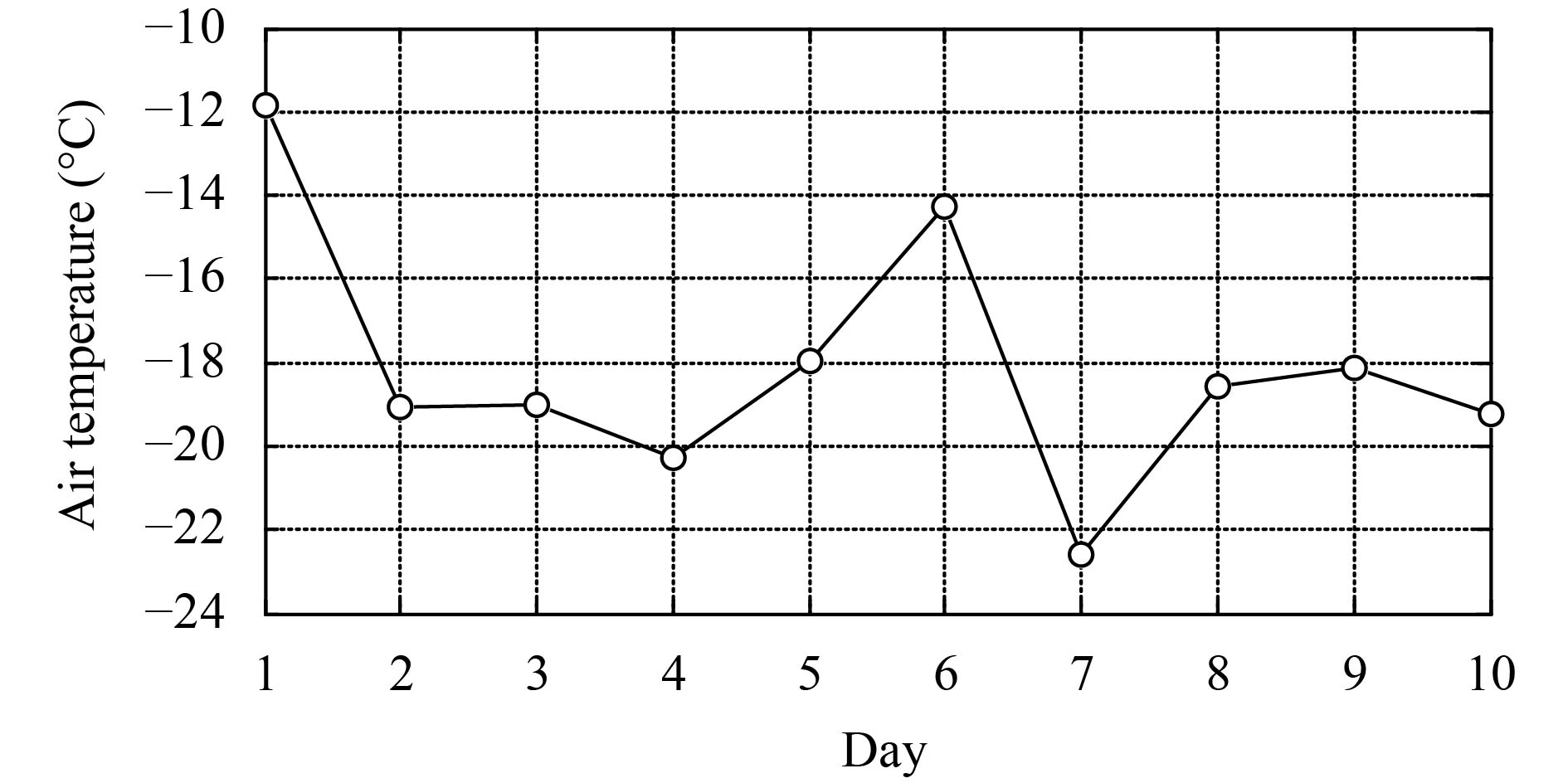
|
图 4 按天的融合结果 |
3 结束语
因为气象数据中的空气温度变化缓慢, 并且受到噪声干扰小, 提出了一种线性模型的改进的卡尔曼滤波融合算法. 它根据数据缓慢变化趋势, 利用上一时刻的估计值和当前时刻的观测值推出当前状态进行融合. 通过仿真实验, 改进的算法能够避免扰动数据和突变数据的干扰, 为同一空间的时间序列数据融合提供新的方法, 为下一步的气象数据的研究奠定基础.
| [1] |
张雪峰, 牛建明, 张庆, 等. 内蒙古锡林河流域草地生态系统土壤保持功能及其空间分布. 草业学报, 2015, 24(1): 12-20. DOI:10.11686/cyxb20150103 |
| [2] |
宋小园, 朱仲元, 张圣微, 等. 锡林河流域气候变化特征诊断分析. 干旱区资源与环境, 2016, 30(4): 151-158. |
| [3] |
李翀, 王沁, 李磊, 等. 一种基于时间序列的节点级数据融合方法. 计算机科学, 2008, 35(11A): 307-311. |
| [4] |
刘卫萍, 王宁, 周晓磊, 等. 数据融合技术在环境监测领域的应用. 计算机系统应用, 2016, 25(6): 88-93. |
| [5] |
张鹏鹏, 俞阿龙, 孙诗裕, 等. 多传感器数据融合在矿井安全监测中的应用. 工矿自动化, 2015, 41(12): 5-8. |
| [6] |
刘超云, 尹小波, 张彬. 基于Kalman滤波数据融合技术的滑坡变形分析与预测. 中国地质灾害与防治学报, 2015, 26(4): 30-35, 42. |
| [7] |
邹波, 张华, 姜军. 多传感信息融合的改进扩展卡尔曼滤波定姿. 计算机应用研究, 2014, 31(4): 1035-1038, 1042. |
| [8] |
Ou Y, Xia YQ, Fu MY. A modified method of nonlinear attitude estimation based on EKF. Proceedings of the 12th International Conference on Control Automation Robotics & Vision (ICARCV). Guangzhou, China. 2012. 901–906.
|
| [9] |
龙慧. 基于Consensus滤波的分布式卡尔曼信息融合方法. 物联网技术, 2011(3): 61-64. |
| [10] |
Das S, Moura JMF. Distributed Kalman filtering with dynamic observations consensus. IEEE Transactions on Signal Processing, 2015, 63(17): 4458-4473. DOI:10.1109/TSP.2015.2424205 |
| [11] |
Ivanjko E, Vasak M, Petrovic I. Kalman filter theory based mobile robot pose tracking using occupancy grid maps. Proceedings of International Conference on Control and Automation. Budapest, Hungary. 2005, 2. 869–874.
|
| [12] |
吴勇, 关胜晓. 基于无迹卡尔曼滤波器的改进SLAM问题求解方法. 计算机系统应用, 2017, 26(3): 30-36. DOI:10.15888/j.cnki.csa.005674 |
| [13] |
周卫东, 乔相伟, 吉宇人, 等. 基于新息和残差的自适应UKF算法. 宇航学报, 2010, 31(7): 1798-1804. |
| [14] |
蔡小庆, 鲁小利, 张伟娟, 等. 基于卡尔曼滤波数据融合的温室监控系统. 电子测试, 2016(6): 59-60. |
| [15] |
Chen YK, Si XC, Li ZG. Research on Kalman-filter based multisensor data fusion. Journal of Systems Engineering and Electronics, 2007, 18(3): 497-502. DOI:10.1016/S1004-4132(07)60119-4 |
| [16] |
Wang J, Xue HR, Jiang XH. Application of Kalman filtering algorithm in greenhouse environment monitoring. Proceedings of the 2013 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation (IMSNA). Toronto, ON, Canada. 2013. 539–544.
|
| [17] |
范满红, 马胜前, 陈彦, 等. 基于多传感器数据融合的温湿度监测系统. 压电与声光, 2012, 34(3): 459-462, 465. DOI:10.11977/j.issn.1004-2474.2012.03.037 |
| [18] |
夏卓君. 分布图法在疏失误差处理中的应用. 实用测试技术, 2002, 28(2): 33-34, 8. |
| [19] |
滕召胜. 基于多传感器数据融合的热处理炉温度测量方法. 计量学报, 2000, 21(2): 148-152. |
 2018, Vol. 27
2018, Vol. 27


