随着我国经济水平的不断提高, 人们住房、生活得到了大幅度的改善, 出现了许多大型建筑. 在建筑构建过程中, 工程造价是大家关心的重要问题, 其直接影响到工程的管理、成本以及其它方面, 因此建立高精度的建筑工程造价预测模型一直是人们关注的焦点[1–3].
建筑工程造价建模常基于时间序列数据进行, 把建筑工程造价看作是一种按时间前后顺序组织在一起的数据, 数据之间存在明显时序特性, 同时受到其它因素影响, 具有较强的非线性变化特点. 传统建筑工程造价预测模型有: 多元性线回归, 滑动平均模型等, 它们属于线性建模方法, 无法描述建筑工程造价的非线性变化特征, 建筑工程造价预测结果不太可靠[4,5]. 近些年, 人们将神经网络引入到了建筑工程造价的建模中, 由于具有非线性预测能力, 获得了比传统模型更高的建筑工程预测精度[6–8]. 神经网络要求建筑工程造价的历史数据多, 如果历史数据太少, 会出现“过拟合”的建筑工程造价预测结果. 支持向量机(Support Vector Machine, SVM)是一种非线性建模能力强的算法, 克服了神经网络对训练样本规模的约束条件, 预测性能要优于神经网络, 为建筑工程造价提供了一种新的建模工具[9]. 如何对历史数据间的时间相关性进行有效挖掘十分关键, 常采用拓阶的方法实现, 拓阶过程消耗时间长, 而且属于线性拓阶方法, 结果无法描述建筑工程造价的非线性变化特性. 为了精确对建筑工程造价进行预测, 根据对建筑工程造价样本时间相关性和非线性变化特点, 构建了基于地统计学与支持向量机相融合的建筑工程造价预测模型, 并通过建筑工程造价预测实例对性能进行测试与分析.
2 支持向量机与地统计学基于支持向量机的建筑工程造价预测建模过程中, 由于根据建筑工程造价数据间的时间相关性, 由支持向量机自身无法确定表示时间相关性的嵌入维数, 地统计学(Geostatistics, GS)[10,11]是一种时序特性分析法, 可以将变程作为时间序列的阶数, 即嵌入维数, 而且工作过程简单、执行速度快, 可以用于确定支持向量机的建筑工程造价时间序列拓阶.
2.1 支持向量机设训练样本集合为:
| $f(x) = w\Phi (x) + b$ | (1) |
式中, w为权向量, b为阈值,
为了使预测结果的风险最小化, 建立如下的经验风险函数:
| ${R_{{emp}}} = \frac{1}{m}\sum\limits_{i = 1}^m {L({y_i} - f({x_i}))} $ | (2) |
式中, L为损失函数, 具体为
| $L( \cdot ) = \left\{ {\begin{array}{*{20}{l}}{0{\kern 1pt}, \;\;\;\;\;\;\;{\kern 1pt} if{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{y_i} - f({x_i})} \right| < \varepsilon }\\{\left| {{y_i} - f({x_i})} \right| - \varepsilon, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} else}\end{array}} \right.$ | (3) |
式中,
对于小样本预测问题, 基于经验风险原理进行建模可能导致预测结果差, 为此支持向量机考虑了泛化风险, 得到如下回归函数:
| $f(x) = \sum\limits_{i = 1}^m {{w_i}{\Phi _i}(x)} + b$ | (4) |
式(4)可以转化为求解以下函数规划问题:
| $\min {\kern 1pt} {\kern 1pt} \left( {\frac{1}{2}{{\left\| w \right\|}^2} + C\sum\limits_{i = 1}^m {\left( {{\xi _i} + \xi _i^*} \right)} } \right)$ | (5) |
约束条件为:
| ${{s.t}}{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{c}}{{y_k} - f({x_k}) \le \varepsilon + {\xi _i}}\\{f({x_k}) - {y_k} \le \varepsilon + \xi _i^*}\\{{\xi _i} \ge 0,{\kern 1pt} {\kern 1pt} \xi _i^* \ge 0}\end{array}} \right.$ | (6) |
式中,
引入拉格朗日算子
| $f(x) = \sum {(\alpha _i^*} - {\alpha _i})K({x_i},x) + b$ | (7) |
式中,
| $K({x_i},{x_j}) = (\Phi ({x_i}) \cdot \Phi ({x_j}))$ | (8) |
本文采用RBF函数, 其定义为
| $K({x_i},x) = \exp \left( {\frac{{\left\| {{x_i} - x} \right\|}}{{2{\sigma ^2}}}} \right)$ | (9) |
在建筑工程造价进行建模时, 相关研究表明, 下一时刻建筑工程造价与前m个建筑工程造价相关, 即时间序列的嵌入维数, 用
| ${y_{k + 1}} = f({y_k},{y_{k - 1}}, \cdots ,{y_{k - m}})$ | (10) |
地统计学(GS)是一种现代统计学理论, 根据变异函数(
| $\gamma (h) = \frac{1}{{2N(h)}}{\sum\limits_{i = 1}^{N(h)} {\left[ {Z({x_i}) - Z({x_i} + h)} \right]} ^2}$ | (11) |
协方差函数定义为:
| $C(h) = E\left[ {Z(x)Z(x + h)} \right] - {m^2}$ | (12) |
式中, h表示时间间隔距离.
3 GS-SVM的建筑工程造价预测模型(1) 收集建筑工程造价相关数据, 得到数据形式为X={x1, x2, …, xn}, 并进行如下处理.
| ${x_{{norm}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} \times 0.8 + 0.1$ | (13) |
(2) 采用地统计学通过变程确定建筑工程造价的最优嵌入维数, 具体为: 根据不同h, 由式(11)得到不同的γ(h), 刚开始, h与γ(h)之间是一种线性变化关系, 当h超过一定距离后, γ(h)得到第一个最大值, 该γ(h)的值为基台值, 此时的h为变程, 用α表示, 即得到了时间序列的嵌入维值.
(3) 根据最优嵌入维数和建筑工程造价的影响因素构建支持向量机的输入向量, 与相应的建筑工程造价组成学习样本.
(4) 将建筑工程造价训练样本集输入支持向量机, 并设置支持向量机参数, 建立建筑工程造价预测模型. GS-SVM的工程造价建模过程如图1所示.

|
图 1 工程造价预测模型的工作流程 |
4 建筑工程造价预测实例 4.1 数据来源
选择某市2000~2016年的每月工程造价数据作为研究对象, 共获得180个样本, 采用单层面积、层数、层高、承载力、基深作为影响, 工程造价数据如图2所示, 以130个月数据作为训练样本, 建立建筑工程造价预测模型, 其余50个样本对建筑工程造价预测模型的泛化能力进行测试.

|
图 2 实验对象 |
从图2可知, 2000~2016年的每月建筑工程造价数据具有明显上升变化态势, 为此建立建筑工程造价模型之前, 对原始数据进行去趋势平稳化法处理, 具体如下:
首先对2000~2016年的每月建筑工程造价数据取对数, 然后进行拟合, 即
| $\ln {y_t} = a + bt$ | (14) |
根据式(14)得到去趋势平稳化后的2000~2016年的每月建筑工程造价数据:
| ${y_t} = \ln {y_y} - (a + bt)$ | (15) |
后续建模基于平稳化后的建筑工程造价数据.
4.2 基于GS确定建筑工程造价数据嵌入维数建筑工程造价不仅与单层面积、层数、层高、承载力、基深等因素有关, 而且与前一段时间的建筑工程造价相关, 因此, 建筑工程造价时间序列具有明显的时间关联特性, 对平稳化后的建筑工程造价数据进行地统计学分析, 得到建筑工程造价的半变异函数如图3所示. 从图3可知, 变程α=5, 即建筑工程造价与前5个月的建筑工程造价相关, 因此嵌入维数为5. 前5个月的建筑工程造价数据与单层面积、层数、层高、承载力、基深作为输入, 构建支持向量机的学习样本.
4.3 结果与分析 4.3.1 GS-SVM的预测结果通过十折交叉验证法确定支持向量机的参数: C=240.80, σ=1.784, GS-SVM的建筑工程造价预测结果如图4所示. 从图4可知, GS-SVM的建筑工程造价预测精度相当高, 能够较好描述建筑工程造价的变化特点, GS-SVM可以应用于实际的建筑工程造价中.

|
图 3 建筑工程造价的半变异函数图 |
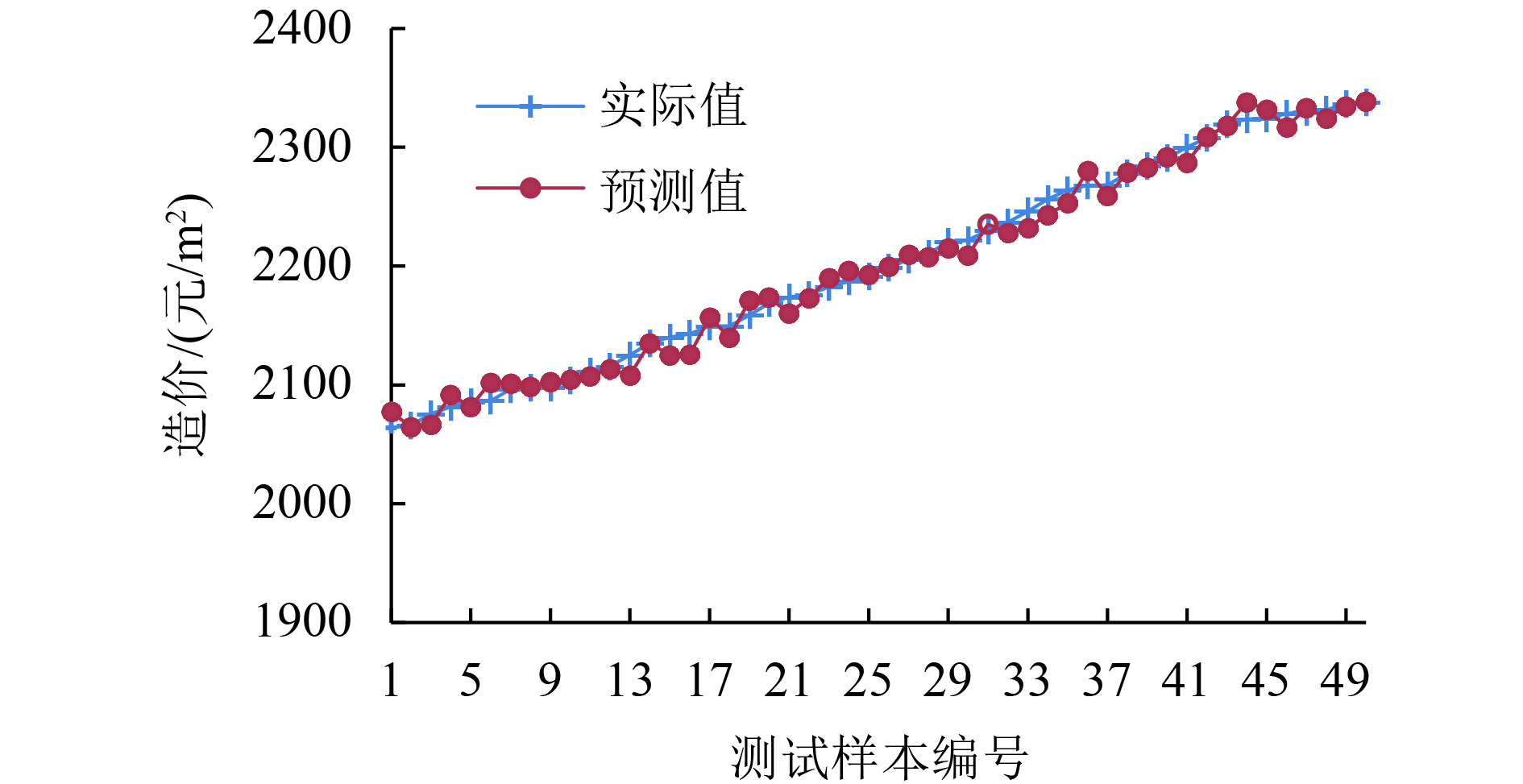
|
图 4 GS-SVM的建筑工程造价预测结果 |
4.3.2 与其它模型的预测结果
比较采用多元线性回归模型(MLR)、支持向量机(SVM)、地统计学与BP神经网络(GS-BPNN)作为对比模型, 采用平均预测精度作为建筑工程造价预测结果好坏评价指标. 统计所有模型的建筑工程造价预测精度, 得到结果如表1所示. 对表1的实验结果进行分析, 可知:
(1) 单一支持向量机(SVM)没有考虑建筑工程造价数据的时序动态特性, 没有进行拓阶操作, 只是简单采用影响因素作为输入变量, 导致建筑工程造价预测精度低.
(2) 多元线性回归模型(MLR)的建筑工程造价最低, 说明其不能准确描述建筑工程造价的变化特点, 获得了较高的建筑工程造价预测误差, 没有什么实际应用价值.
(3) GS-BPNN的建筑工程造价平均预测精度得到了一定提升, 这主要由于通过GS对建筑工程造价时间序列进行拓阶处理, 描述了数据的时序动态特性, 大幅度降低了建筑工程造价的预测误差, 表明引入变程可以有效提高建筑工程造价预测精度.
(4) GS-SVM的建筑工程造价预测精度最高, 这是因为采用支持向量机对建筑工程造价进行建模, 克服了神经网络大样本要求, 泛化能力优异, 并通过GS描述建筑工程造价数据的时序特性, 建立理想的建筑工程造价预测模型, 相比对比模型, 建筑工程造价预测精度具有明显优势.
| 表 1 建筑工程造价的预测精度对比 |
5 结束语
针对建筑工程造价中的训练样本选择问题, 以及非线性变化特点, 综合利用地统计学和支持向量机的优点, 设计了基于GS-SVM的建筑工程造价预测模型, 通过地统计学快速确定时间序列的嵌入维数, 然后通过支持向量机建立建筑工程造价的非线性预测模型, 具体应用实例测试结果表明, GS-SVM大幅度提高了建筑工程造价的预测精度, 具有广泛的应用前景.
| [1] |
陈鹏, 刘亚南. 建筑工程造价管理的现状与对策. 工业工程, 2015, 34(48): 33-34. |
| [2] |
张利荣. 多基元模糊算法在工程估价中的应用. 施工技术, 2010, 39(6): 64-66. |
| [3] |
胡六星. 基于时间序列的建筑工程造价预测研究. 太原理工业大学学报, 2012, 43(6): 706-709, 714. |
| [4] |
郭一斌, 王红革, 王翔. 基于Vague集贴近度的工程项目投资快速估算方法. 现代经济信息, 2011, 12(2): 50-55. |
| [5] |
孟俊娜, 梁岩, 房宁. 基于BP神经网络的民用建筑工程造价估算方法研究. 建筑经济, 2015, 36(9): 64-68. |
| [6] |
胡晓娟. 多元线性回归模型参数的STLS估计法及其在工程造价预测中的应用. 四川建筑科学研究, 2016, 42(4): 142-147. |
| [7] |
牛东晓, 乞建勋, 邢棉. 建筑工程造价预测的变结构神经网络模型研究. 华北电力大学学报, 2001, 28(4): 1-4. |
| [8] |
李杰. 改进粒子群算法优化支持向量机的工程造价预测. 计算机系统应用, 2016, 25(6): 202-206. |
| [9] |
Li GQ, Deng M, Zhu JJ, et al. Spatial outliers detection considering distances among their neighbors. Journal of Remote Sensing, 2009, 13(2): 197-202. |
| [10] |
Petitgas P, Woillez M, Doray M, et al. A geostatistical definition of hotspots for fish spatial distributions. Mathematical Geosciences, 2016, 48(1): 65-77. DOI:10.1007/s11004-015-9592-z |
| [11] |
刘莘, 张绍良, 王飞, 等. 基于地统计学的空间离群点检测算法的研究. 计算机应用研究, 2016, 33(12): 3700-3704. DOI:10.3969/j.issn.1001-3695.2016.12.040 |
| [12] |
王雪松. 改进支持向量机的网络流量预测. 计算机系统应用, 2017, 26(3): 230-233. |
 2018, Vol. 27
2018, Vol. 27


