随着人们生活水平的不断提高, 人们对室内环境热舒适的要求也日益提高. 现有温度控制已不能满足人们对室内舒适性的要求. 因此, 有学者就尝试将热舒适度作为空调系统的控制目标, 结果表明, 这样不仅满足了室内环境的舒适性, 同时还降低了空调系统的能耗, 达到节能的效果[1,2]. 由于热舒适度计算的复杂性和非线性, 无法直接用于空调的实时控制系统, 因此, 需要建立一个能够准确预测室内热舒适度的模型.
随着智能优化算法的不断发展, 学者提出了很多用于预测热舒适度的算法, 比如模糊聚类算法[3,4]、人工神经网络算法[5]、BP神经网络算法[6]. 其中相对其他算法, BP神经网络训练复杂性低、预测精度高, 所以将采用BP神经网络对PMV值进行预测, 但它也存在收敛慢、易出现局部最小等缺陷, 需要对其参数进行优化. 常用的优化算法包括: 粒子群(PSO)算法[7–9]、蚁群算法(ACO)[10,11]、遗传算法(GA)[12]等, 但这些优化算法都存在早熟收敛、局部寻优能力差等缺点. 本文介绍了一种新型的类似PSO算法的优化算法——鸟群算法(BSA), 它不仅具有PSO算法的优点, 同时因其多样性的优点, 有效地避免了早熟收敛. 最后, 通过与PSO算法的优化效果进行对比, 也表明BSA算法的优化效果更强, 实用性更高.
1 热舒适度指标热舒适是人体对室内环境表示满意的意识状态. 预测平均投票指标(PMV)是热舒适的一个较全面的指标, 代表了同一环境大多数人的感觉. 主要影响因素包括: 平均辐射温度、空气温度、湿度、风速、人体的新陈代谢和人体的热阻.
PMV指标的范围为[–3 3], 分为7等级分度, 见表1.
| 表 1 PMV指标的分度表 |
PMV指标数学模型为[13]:
| $\begin{split}{{PMV}} = & [0.303\exp ( - 0.036M) + 0.0275] \times \{ M - W - 3.05[5.733 - 0.007(M - W) - {P_a}] -0.42(M - W - 58.2) - \\ & 0.0173M(5.867 - {P_a}) - 0.0014M(34 - {t_a}) - 3.96 \times {10^{ - 8}}{f_{cl}}{[{t_{cl}} + 273)^4} - {({t_r} + 273)^4}] - {f_{cl}}{h_c}(tcl - {t_a})\end{split}$ | (1) |
| ${t_{cl}} = {{ }}35.7 - 0.028(M - W) - {I_{cl}}\left\{ {3.96 \times {{10}^{ - 8}}{f_{cl}}} \right.\left. {\left[ {{{\left( {{t_{cl}} + 279} \right)}^4} - {{\left( {{t_r} = 273} \right)}^4}} \right] + {f_{cl}}{h_c}\left( {{t_{cl}} - {t_a}} \right)} \right\}$ | (2) |
| ${f_{cl = }}\left\{ {\begin{array}{*{20}{c}}{1.00 + 1.290\;{I_{cl}}\;\;\;\;\;\;\;\;\;\;{\text{当}}{I_{cl}} \le 0.078}\\{1.05 + 0.645\;{I_{cl}}\;\;\;\;\;\;\;\;\;\;{\text{当}}{I_{cl}} > 0.078}\end{array}} \right.$ | (3) |
| ${h_{c = }}\left\{\!\!\! {\begin{array}{*{20}{c}}{0.38{{({t_{cl}} - {t_a})}^{0.25}}\;\;\;{\text{当}}\;0.38{{({t_{cl}} \!-\! {t_a})}^{0.25}}\! > \!12.1\!\!\!\sqrt {{V_a}} }\\\!\!\!{12.1\sqrt {{V_a}} \;\;\;\;\;\;\;\;\;\;\;\;{\text{当}}0.38{{({t_{cl}} - {t_a})}^{0.25}}\! \le \!12.1\!\!\sqrt {{V_a}} }\end{array}} \right.$ | (4) |
模型符号说明如表2所示.
| 表 2 模式符号说明 |
2 热舒适度的预测算法描述 2.1 BP神经网络
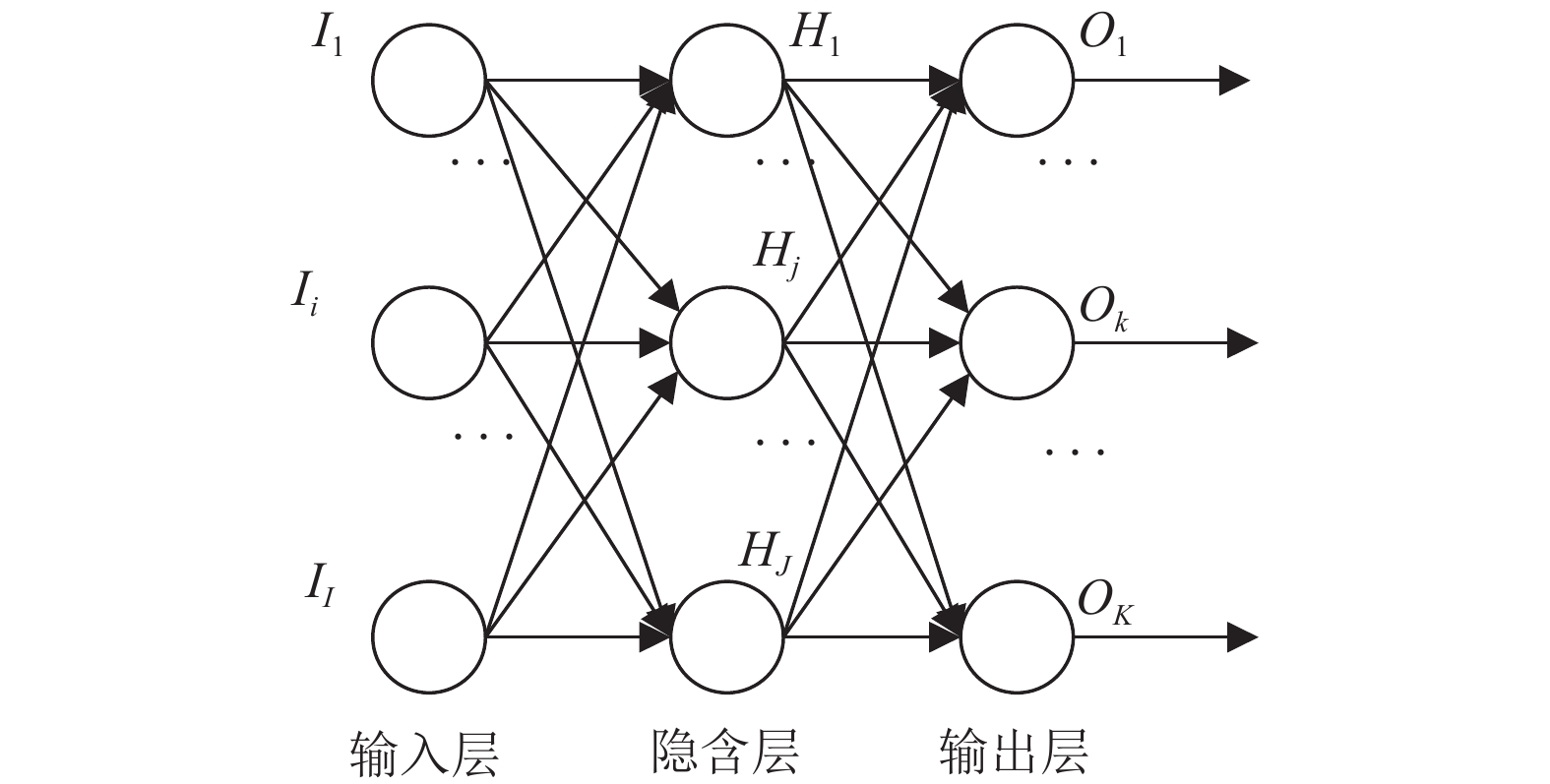
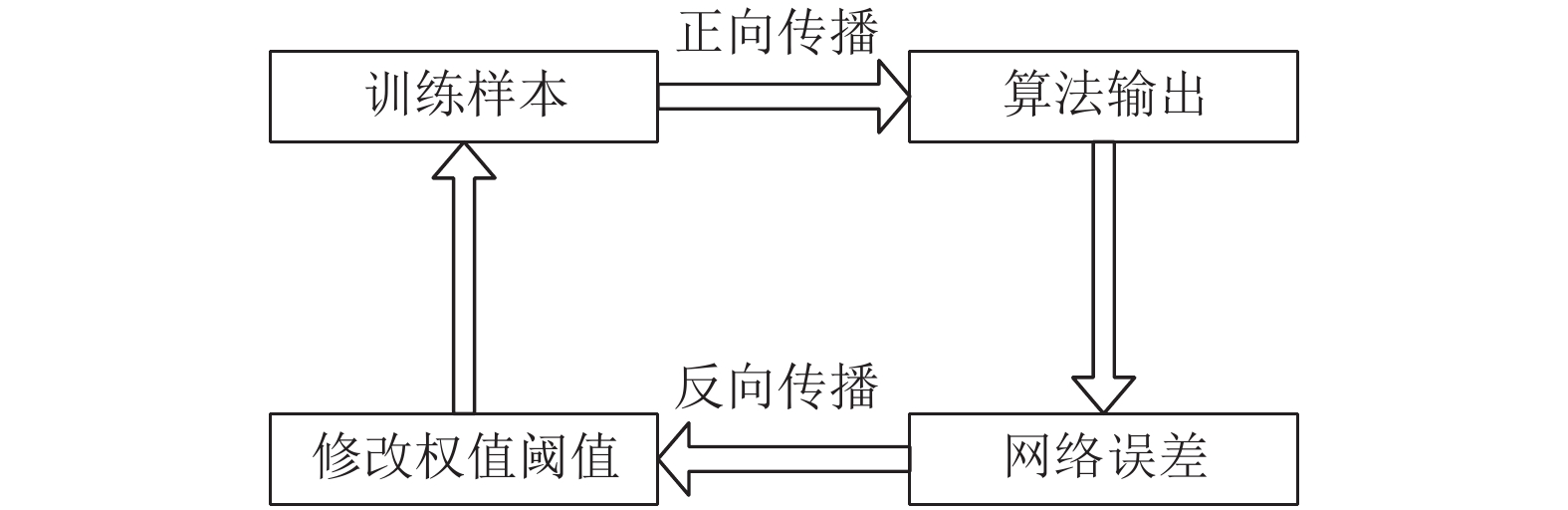
BP神经网络是一种按误差逆向传播算法训练的多层前馈网络, 主要由输入层、中间层和输出层组成, 拓扑结构如图1所示[14,15]. BP神经网络是通过不断对样本进行训练, 并调整网络的权值与阈值, 使输出值与期望值间的误差最小. BP神经网络算法主要包括两部分: 信号正向传播与误差反向传播. 其算法示意图如图2所示[14].
|
图 1 三层前馈神经网络 |
|
图 2 BP神经网络学习算法示意图 |
BP神经网络算法学习过程: 正向传播时, 样本信号通过输入层、隐含层和输出层被逐层处理, 网络的权值不变, 且同层的神经元只作用于后一层的神经元. 当输出值达不到预期值时, 则进行误差反向传播. 误差反向传播时, 误差信号通过从输出层向隐含层、输入层逐层传播. 通过误差不断调整网络的权值与阈值, 使均方误差最小, 从而使得输出值更接近期望值.
2.2 鸟群算法(BSA)文献[15]表明, 鸟类主要是通过觅食行为、警戒行为和飞行行为3种行为共享信息, 而获取生存优势. 鸟群算法的灵感起于鸟群, 它是基于信息共享机制及搜索策略而发展起来的一种新型全局优化算法.
设鸟N群规模为, 搜索空间的维数为D, 第i只鸟在觅食空间中第t时刻的位置可表示为
如果一个在(0,1)范围内均匀分布的随机数小于
觅食行为的数学描述为:
| $\begin{array}{c}x_{i,j}^{t + 1} = \;x_{i,j}^t + ({P_{i,j}} - x_{i,j}^t) \times C \times rand\;\,(0\,,\,1)\\ + ({g_j} - x_{i,j}^t) \times S \times \;rand\;\,(0\,,\,1)\end{array}$ | (5) |
警戒行为的数学式描述为:
| $\begin{array}{c}x_{i,j}^{t + 1} = \;x_{i,j}^t + A1\,(mea{n_j} - x_{i,j}^t) \times rand\;\,(0\,,\,1)\\ + A2\,({p_{k,j}} - x_{i,j}^t) \times \;rand\;\,( - 1\,,\,1)\end{array}$ | (6) |
| $A1 = a1 \times \exp \left( { - \frac{{pFi{t_i}}}{{sumFit + \varepsilon }} \times N} \right)$ | (7) |
| $A2 = a2 \times \exp \left( {\left( {\frac{{pFi{t_i} - pFi{t_k}}}{{\left| {pFi{t_k} - pFi{t_i}} \right| + \varepsilon }}} \right)\frac{{N \times pFi{t_k}}}{{sumFit + \varepsilon }}} \right)$ | (8) |
飞行行为中生产者和索取者的行为数学描述分别为:
| $x_{i,j}^{t + 1} = x_{i,j}^t + rand(0,1) \times x_{i,j}^t$ | (9) |
| $x_{i,j}^{t + 1} = x_{i,j}^t + (x_{k,j}^t - x_{i,j}^t) \times FL \times rand(0\,,\,1)$ | (10) |
上述公式符号说明如表3所示.
BSA算法与PSO算法均是模仿鸟群在自然界中的行为提出的, 其中PSO算法只是单纯的模仿了鸟群的觅食行为, 而BSA算法模仿了觅食行为、警戒行为和飞行行为3种行为. BSA算法是一种先天的集成算法, PSO算法则是在适当简化下的BSA算法的特殊情况, 其觅食公式与PSO算法公式的相似, 所以BSA算法具有PSO算法的优势, 即收敛速度快、全局搜索能力强、鲁棒性能好等优点. BSA算法又模仿了鸟类的警觉行为和生产者的行为, 所以又具有自己的特征.
因BSA算法具有4种搜索策略, 使其能灵活调整不同搜索策略并更易于扩展, 可看出它具有良好的多样性和稳定性. 相对PSO算法易陷入局部最优解与易早熟收敛的劣势, BSA算法则更加稳定且可避免早熟收敛. 总之, BSA算法的性能优于PSO算法, 具有更高的精度、效率、稳定性、收敛性和鲁棒性能.
2.3 BSA算法优化BP神经网络BSA算法优化BP神经网络的基本思想[16]是: 利用BSA算法的全局搜索能力, 优化BP神经网络初始的权值和阈值, 也就是决策变量, 其中每一组决策变量均包含在鸟群个体所处的空间位置中. 然后, 通过适应度函数来衡量个体所处空间位置的优劣度, 并利用鸟群觅食过程中的觅食行为、警戒行为和飞行行为等策略不断更新个体空间位置, 直至获取最佳的个体空间位置, 即获得待优化问题的最佳决策变量.
| 表 3 公式符号说明 |
BSA-BP算法预测PMV指标主要包括以下几个部分: 确定训练样本数据、设计BP神经网络结构、利用BSA算法优化BP神经网络初始的权值和阈值、训练优化后的网络. 具体实现步骤如下:
步骤1. 确定训练样本数据. 确定所需输入变量的取值范围; 然后, 根据PMV指标的数学模型, 利用MATLAB软件编辑PMV指标的计算程序, 获取相当数量的样本数据; 最后, 经过预处理, 作为BP神经网络的训练样本和测试样本数据.
步骤2. 设计BP神经网络结构. 依据标准BP神经网络模型以及PMV指标的数学模型, 确定BP神经网络的层数、每层的神经元数, 以及其他参数.
步骤3. 确定BSA算法中各参数. 包括初始化种群规模N、搜索空间维数D、最大迭代次数T、飞行间隔FQ、觅食概率P、常量C、S、a1、a2、FL以及随机初始化鸟群个体空间位置xti.
步骤4. 计算BSA算法的适应度函数值, 将样本的均方误差作为适应度函数, 找到最小的适应度值, 并保留当前最好个体空间位置. 判断算法终止条件是否满足, 若满足则转至步骤6, 否则执行步骤 5.
步骤5. BSA算法优化BP神经网络初始的权值和阈值. 依据BSA算法的步骤, 不断迭代进行寻优, 直到迭代停止, 输出全局最优值, 也就是最优网络初始的权值和阈值, 并将其赋给BP神经网络.
步骤6. 训练BSA算法优化后的BP神经网络. 网络经训练结束后, 将得到最佳的PMV指标预测模型.
上面所述的实现步骤可见图3

|
图 3 改进的BSA算法优化BP神经网络的流程 |
3 热舒适度预测模型的仿真 3.1 准备样本数据
依据传统的PMV计算公式, 确定各输入变量的取值范围, 并在其范围内, 随机生成1400组数据作为样本数据. 为了较好的训练效果, 须对数据归一化预处理, 并将数据分为1200组的训练样本和200组的测试样本. 输入变量的取值范围[17,18]如下:
人体新陈代谢率M: 55 ~75 W/m2;
服装热阻
空气温度
空气相对湿度
空气流动速度
平均辐射温度
人体对外做功
因单隐层能反映大部分的非线性关系, 因此, 采用三层网络结构来构建PMV预测模型. 从PMV数学模型中可知, 有6个输入量, 1个输出量, 所以网络的输入层节点数为6, 输出层节点数为 1; 可依据下面的经验公式确定隐含层的神经元数目[18]:
| ${n_1} = \sqrt {n + m} + a$ | (11) |
式中, n为输入神经元节点数; m为输出神经元节点数;
确定BP网络的结构为 6-10-14; 最大步数为 1000; 学习率为0.01; 学习目标为 0.00001; 激活函数选取S型函数.
|
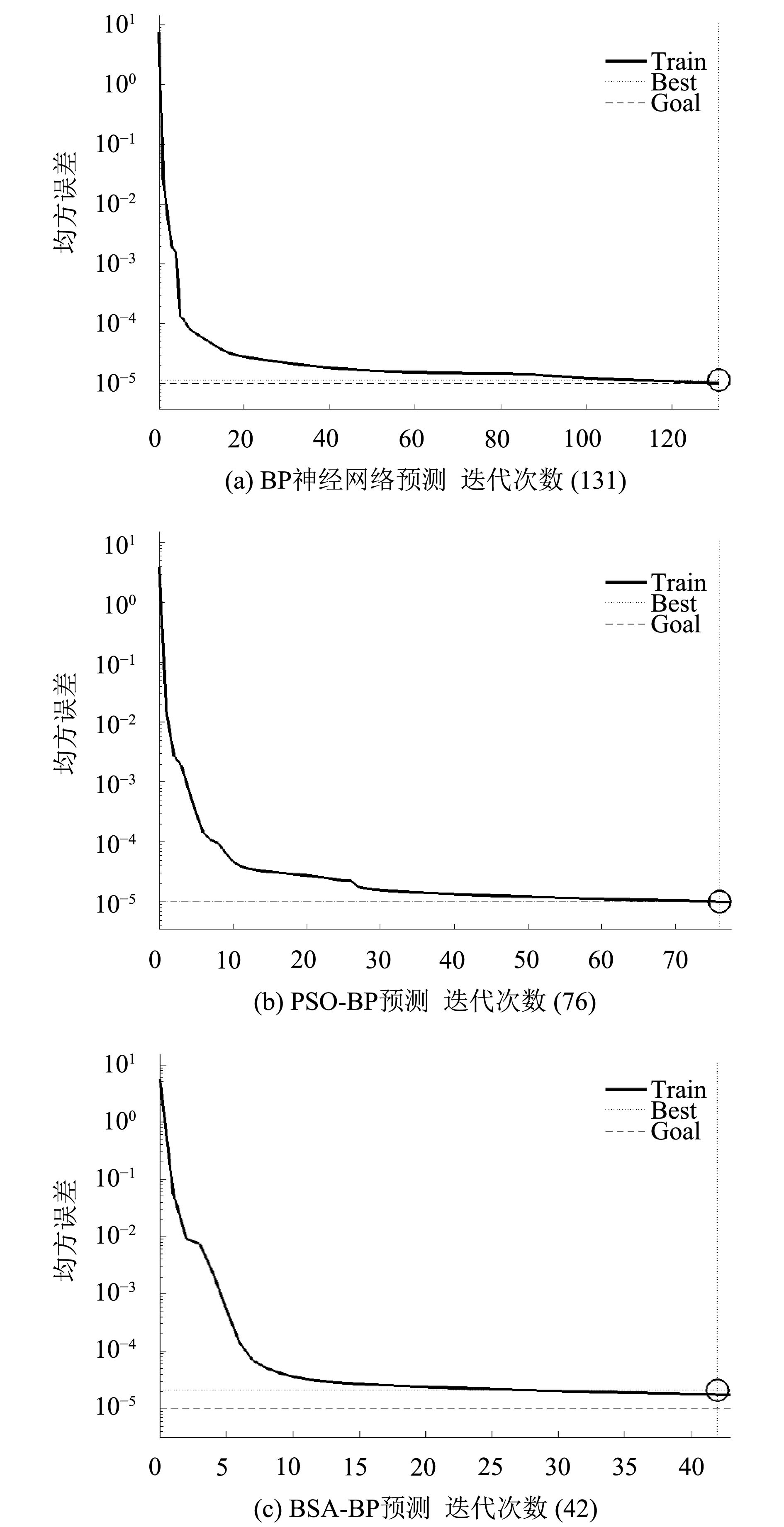
图 4 预测模型的收敛曲线图 |
BSA算法的参数设置如下: 搜索空间维数
在上述算法的参数设置及样本数据的基础上, 构建了PSO-BP算法和BSA-BP算法的预测PMV指标的模型, 并在MATLAB的运行环境下进行仿真. 为评判不同预测模型性能的好坏, 在采用相同样本数据和算法参数的条件下, 对传统的BP预测模型、PSO-BP预测模型与BSA-BP预测模型进行仿真对比分析.
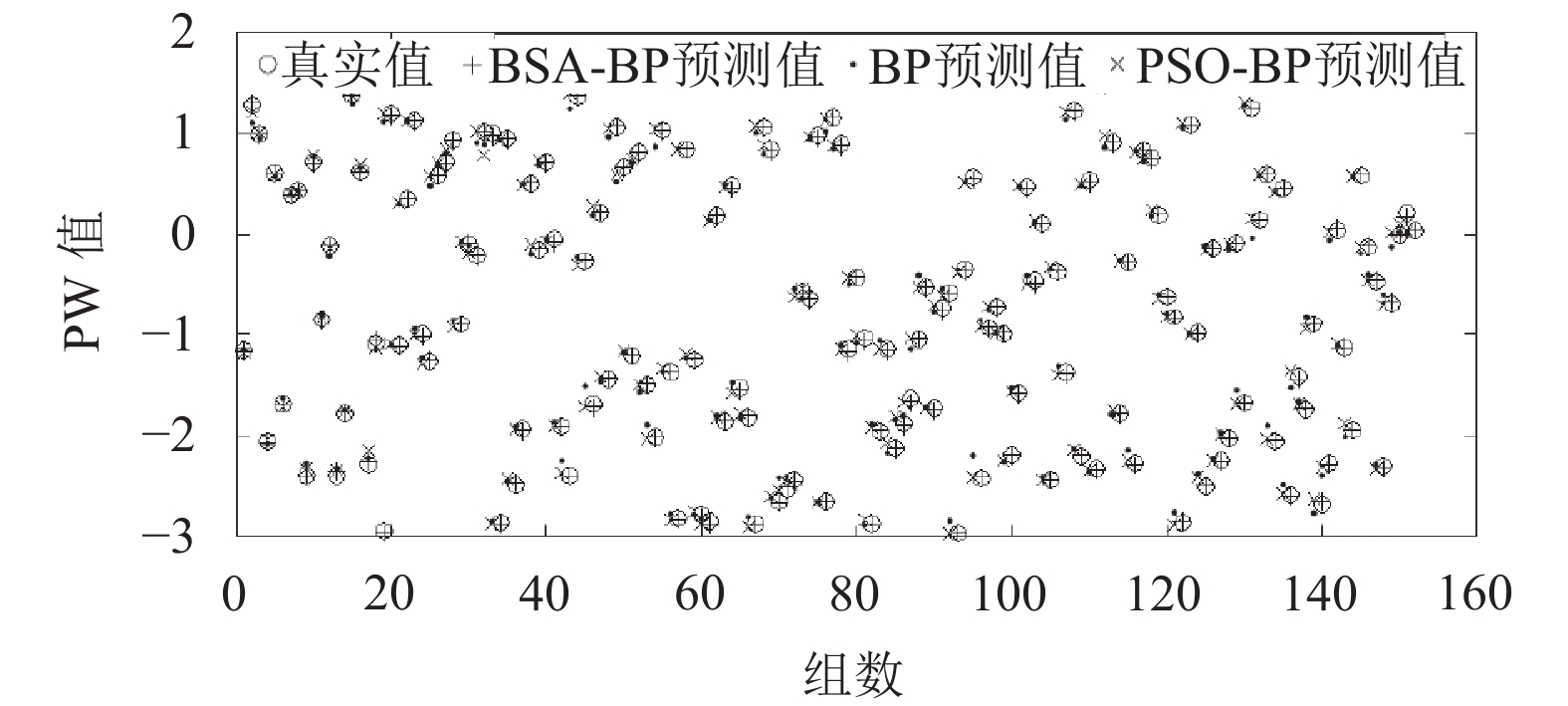
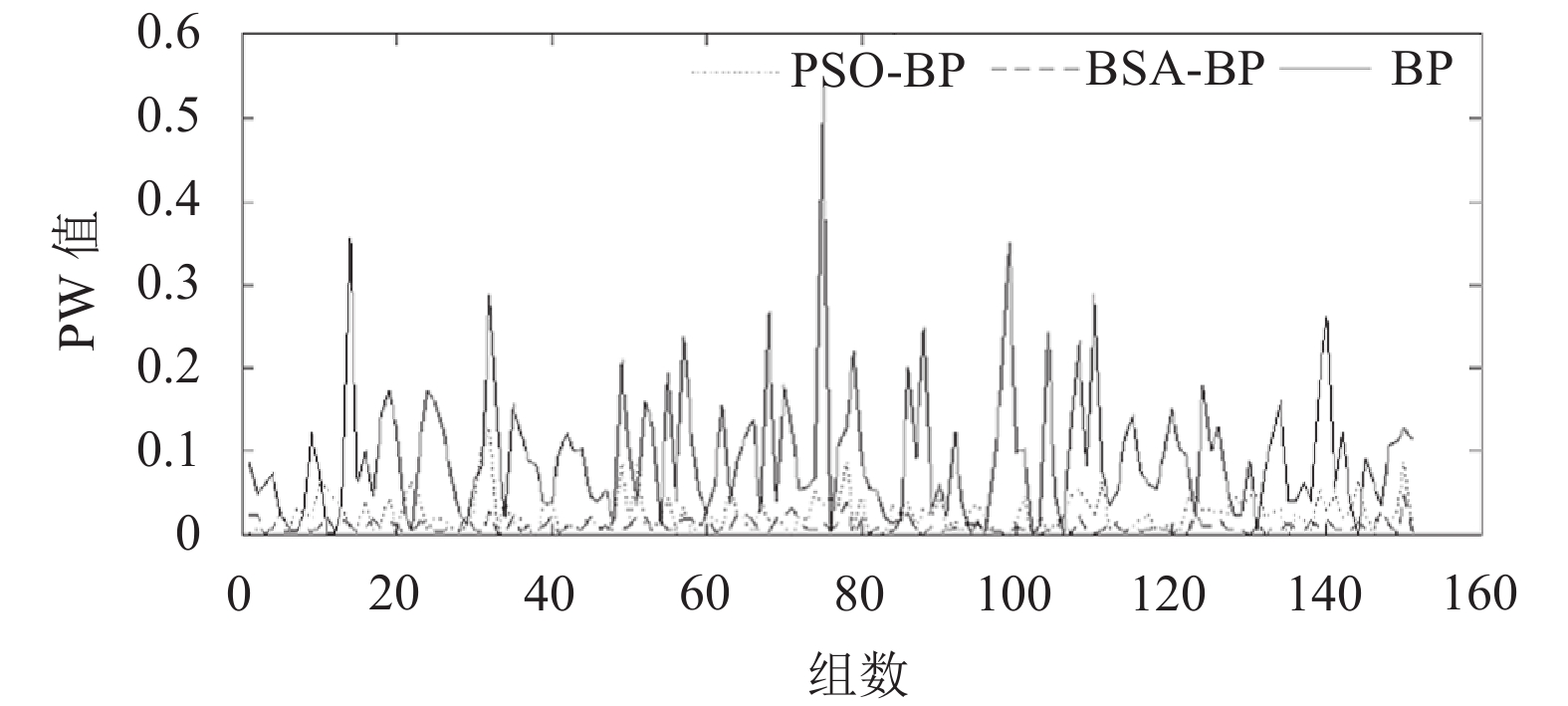
图4是预测模型的均方误差变化曲线图; 图5是200组测试样本中PMV值在[–3,3]范围内, 预测模型的拟合效果图; 图6是预测模型的绝对误差曲线图; 表4是预测模型的3种性能对比. 结果显示, 相对于其余两种预测模型, BSA-BP预测模型有较快的收敛速度和较高的精度.
|
图 5 预测模型的拟合效果图 |
|
图 6 预测模型的绝对误差曲线图 |
| 表 4 预测模型的3种性能对比 |
4 结语
本文首先对预测热舒适度算法的基本原理进行了简单简介. 然后, 用BP神经网络预测热舒适度, 但为了改善传统的BP神经网络的收敛速度慢及局部最优的缺点, 又采用了BSA算法优化BP网络初始的权值和阈值, 来提高模型的精度和算法的收敛速度. 最后, 利用MATLAB软件对传统的BP预测模型、PSO-BP预测模型与BSA-BP预测模型进行仿真实验, 并对实验结果进行比较分析, 结果显示基于BSA-BP预测模型有较快的收敛速度和较高的预测精度.
| [1] |
段培永, 刘聪聪, 段晨旭, 等. 基于粒子群优化的室内动态热舒适度控制方法. 信息与控制, 2013, 42(1): 100-110. |
| [2] |
杨昌智, 张清琳, 杨菊菊, 等. 定温控制空调系统的舒适性及节能性分析. 湖南大学学报(自然科学版), 2012, 39(5): 18-22. |
| [3] |
徐远清, 陈祥光, 王丽, 等. 一种基于模糊因果聚类的室内热舒适预测方法. 仪器仪表学报, 2006, 27(S1): 850-852. |
| [4] |
徐巍, 陈祥光, 彭红星, 等. 基于模糊C-均值聚类与支持向量机的PMV指标预测系统. 系统工程理论与实践, 2009, 29(7): 119-124. DOI:10.12011/1000-6788(2009)7-119 |
| [5] |
Castilla M, Álvarez JD, Ortega MG, et al. Neural network and polynomial approximated thermal comfort models for HVAC systems. Building and Environment, 2013, 59: 107-115. DOI:10.1016/j.buildenv.2012.08.012 |
| [6] |
Cao Y, Tian LW, Zhao HW. The application of BP neural net real-time data forecasting model used in home environment. Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER). Shenyang, China. 2015. 1486–1490.
|
| [7] |
张卉. 基于粒子群优化BP神经网络的房价预测. 价值工程, 2012, 31(14): 207-209. DOI:10.3969/j.issn.1006-4311.2012.14.120 |
| [8] |
赵梅香. 基于粒子群和BP神经网络的PMV预测模型在智能办公建筑中应用研究[硕士学位论文]. 广州: 华南理工大学, 2012.
|
| [9] |
沈学利, 张红岩, 张纪锁. 改进粒子群算法对BP神经网络的优化. 计算机系统应用, 2010, 19(2): 57-61. |
| [10] |
闫婷. 基于蚁群与神经网络算法的变风量空调末端控制研究[硕士学位论文]. 西安: 西安建筑科技大学, 2015.
|
| [11] |
年浩, 顾沈明, 李雪. 基于蚁群优化的BP神经网络对于水质预测的应用. 闽南师范大学学报(自然科学版), 2014(1): 62-67. |
| [12] |
李松, 刘力军, 解永乐. 遗传算法优化BP神经网络的短时交通流混沌预测. 控制与决策, 2011, 26(10): 1581-1585. |
| [13] |
曹勇. 面向室内热湿环境热舒适度预测与控制模型优化研究[硕士学位论文]. 沈阳: 沈阳大学, 2016.
|
| [14] |
樊振宇. BP神经网络模型与学习算法. 软件导刊, 2011, 10(7): 66-68. |
| [15] |
Meng XB, Gao XZ, Lu LH, et al. A new bio-inspired optimisation algorithm: Bird swarm algorithm. Journal of Experimental & Theoretical Artificial Intelligence, 2016, 28(4): 673-687. |
| [16] |
刘天舒. BP神经网络的改进研究及应用[硕士学位论文]. 哈尔滨: 东北农业大学, 2011.
|
| [17] |
张玲. 空调热舒适度预测及控制算法研究[硕士学位论文]. 长沙: 湖南大学, 2014.
|
| [18] |
刘慧芳. 基于室内热舒适的空调系统测控与节能研究[硕士学位论文]. 重庆: 重庆大学, 2009.
|
 2018, Vol. 27
2018, Vol. 27



