安全电子交易协议(Secure Electronic Transaction, SET), 是一个安全的电子支付模型, 它主要为了解决用户、商家、银行的支付交易行为. SET的出现在最大程度上帮助交易参与方提高了交易的信任度, 也保证了交易信息的安全性和完整性. 参与SET一次完整流程的成员有: 持卡者、商家、银行(包括发卡行与收单行)、支付网关以及认证中心. 其中持卡人是支付卡持有者, 得到了发行者的授权; 发卡行是给持卡者发行信用卡的金融机构; 商家是提供货物或服务的经营者; 发卡行是给商家提供开设帐号的金融机构; 收单行也是一个金融机构, 它是接受付款的最终端, 为商家建立一个账户并处理支付卡授权和支付; 支付网关是金融网的安全屏障与关口, 实现对支付信息从Internet到银行内部网络的转换, 用来处理支付功能, 并对商家和持卡人进行认证; 认证中心是参与交易各方都信任的第三方中介组织, 为交易过程中的成员进行身份验证[1,2].
SET核心技术包括数字签名、数字证书、加密算法体制等. 其中SET中的加密算法体制主要应用于支付过程中的数据交换, 在一般的SET支付环境中使用的公钥加密算法是RSA的公钥密码体制. 本文针对SET中的加密算法体制进行研究改进.
1 椭圆曲线加密算法椭圆曲线加密算法(Elliptic Curve Cryptography, ECC)[3–6]是基于椭圆曲线离散对数问题的密码体制, 相对于别的算法, 它的每bit安全性最高. 相比RSA密码体系, ECC体系无论在安全性能上还是通信带宽上都具有一定的优势, 文献[3]中对相同安全级别下的ECC和RSA的密钥长度和密码长度进行了对比, 结果显示随着对于安全性能的要求加强, RSA算法的密匙长度增加的越快, ECC比RSA的硬件要求就更低.
椭圆曲线常用的定义的有限域包括两种: 素数域GF(p)和二进制域GF(2m). 在二进制域上, 元素在计算机中可实现并行的加、减、乘等操作, 因此硬件实现的椭圆曲线加密系统中通常使用二进制域的椭圆曲线加密方法. GF(2m)上一个非奇异椭圆曲线E由Weierstrass公式定义的: y2+xy=x3+ax2+b. 其中a, b是GF(2m)中的元素, 且b≠0. 同时曲线E包括一个无穷远点作为曲线上点的加法单位元, 用O表示. 令P1=(x1, y1), P2=(x2, y2), 是E上的两个点, 且P1≠–P2, 则P3=P1+P2=(x3, y3)可由下式计算:
1) P1≠P2
| $\left\{ \begin{array}{l}\lambda = \left( {{{{y}}_{{2}}} + {y_1}} \right)/\left( {{x_2} + {x_1}} \right)\\{x_3} = {\lambda ^2} + \lambda + {x_1} + {x_2} + a\\{y_3} = \lambda \left( {{x_1} + {x_3}} \right) + {x_3} + {y_1}\end{array} \right.$ |
2) P1=P2
| $\left\{ \begin{array}{l}\lambda = {{{y}}_{{1}}}/{x_1} + {x_1}\\{x_3} = \lambda + \lambda + a\\{y_3} = \lambda \left( {{x_1} + {x_3}} \right) + {x_3} + {y_1}\end{array} \right.$ |
ECC的加密、解密过程, 公钥协议都要求计算椭圆曲线数乘运算.
方案流程:
首先选择一个基域F, 定义一个点P为该域上的椭圆曲线E和F上为素数阶, 点的坐标以(xp, yp)表示. 有限域F, 域元素a和b为椭圆曲线的参数, 公开信息为点P和阶n. 系统建立后每个使用者将会生成各自的密钥.
1) 选取一个随机证书d, d在区间[1, n–1]内
2) 计算点Q=dP;
3) Q为实体的公开密钥, 整数d则为实体的私钥.
生成密钥后的每个使用者将进行加密处理, 当实体B给实体A发送一条信息M时, 实体B执行步骤:
① 查找A的公开密钥Q;
② 将信息M表示为域元素M∈Fq;
③ 选择一个随机整数k, k属于区间[1, n–1];
④ 计算点(x1, y1)=kP;
⑤ 计算点(x2, y2)=kQ;
⑥ 计算c=mx2. 传送加密数据(x1, y1, c)给A.
当实体B完成步骤后进行解密过程后, 实体A解密实体B传输的密文(x1, y1, c), A执行步骤:
(a) 使用他的私钥d, 计算点(x2, y2)=d(x1, y1);
(b) 通过计算m=c×x2–1, 解析出数据m.
上述过程中, Q=dP为公开的, 若存在第三者能够解开上述的椭圆曲线上的离散对数问题, 即能从dP中求出d, 就可得到解密的消息.
2 椭圆曲线数乘算法在有限域中曲线上的两个互异点相加, 需要1次求逆, 2次乘法, 1次平方, 9次加法(在有限域中加法的运算耗时相当少, 通常略去不考虑). 由椭圆曲线密钥交换协议可知, 要提高加解密速度必须提高点的数乘的效率. ECC的加密、解密过程所要求计算的椭圆曲线数乘运算的计算如下形式:
| ${{Q}} = {{kP}} = \underbrace {{{P}} +\cdots+ P}_{k次}$ |
其中P为椭圆曲线上一点, k=(an–1, an–2,…, a2, a1, a0).
2.1 典型算法算法1. 计算从左到右二进制点乘方法
输入: k=(an–1, an–2,…, a2, a1, a0), P为椭圆曲线上一点. 输出: kP.
1. Q=O;
2. 对i从n–1到0, 重复执行
(1) Q=2Q;
(2) 如ai=1, 则Q=Q+P;
3. 返回Q.
该算法平均需要(m–1)次倍乘, (m–1)/2次点加, 其平均计算时间复杂度是记为: t1=(m/2)A+(m–1)D.
NAF (Non-Adjacent Form)表示形式是, 在二进制域椭圆曲线上, 设P=(x, y), 则–P=(x, x+y). 大整数k表示为
算法2. 二进制NAF方法的椭圆曲线数乘算法
输入: 正整数k, 椭圆曲线上一点P.
输出: kP.
1. 计算
(1) i←0;
(2) k≥1时, 重复执行
① 若k是奇数, 则ki←2–(k mod 4), k←k–ki;
② 否则, ki←0;
③ k←k/2, i←i+1;
(3) 返回(ki, ki–1, ki–2,…, k1, k0);
2. Q=O;
3. 对于i从m–1到0, 重复执行
(1) Q=2Q;
(2) 如ai=1, 则Q=Q+P;
(3) 如ai=–1, 则Q=Q–P;
4. 返回Q.
NAF形式的期望权重为m/3, 因而计算其平均计算时间复杂度是t2=(m/3)A+(m−1)D.
算法3. Montgomery数乘算法
输入: k=(an–1, an–2, …, a2, a1, a0), P为椭圆曲线上一点.
输出: kP.
1. Q=O;
2. 对i从n–1到0, 重复执行
(1) Q=2Q;
(2) 如ai=1, 则Q=Q+P;
3. 返回Q.
算法3的平均时间复杂度是t3=(m–1)A+(m−1)D.
结合文献[7]的NAF算法本文给出了一个改进的NAF算法, 具体见算法4.
算法4. 改进的NAF算法
输入: k=am(am–1, …,a0)a–1a–2, ama–1a–2=0(为了方便计算, 我们在最左 边添加0, 同时在末尾添加00, 表示不产生进位), P为椭圆曲线 上一点.
输出: kP.
1. s, t←m+1; change, begin, end, count←0; Q=P;
2. 对于t从m+1到–1, 重复执行
如atat–1=01
begin←1; Q=2Q; Q=Q+abeginP ;
如atat–1!=00, 重复
如atat–1=11,
change←1; end←t–1; t=t–1;
如change=1,
当abeginabegin–1abegin= 010,
判断Rcount;
如Rcount! =0
begin←t–2; count←count+1; abegin=1; Q=2Q; Q=Q+abeginP.
begin=begin–1.
如begin!=end, 重复
abegin=abegin–1;
abeigin=–1.
如begin!=t, 重复
Q=2Q; Q=Q+abeginP ;
begin=begin–1.
否则begin=begin–1.
如begin!=end, 重复
Q=2Q; Q=Q+abeginP ;
否则Q=2Q.
begin←0; change←0; end←0.
3.返回Q.
改进算法使用随机的带符号二进制表示, 其随机性主要通过用011替换二进制表示的
表1对上述算法进行了平均计算时间复杂度的比较.
| 表 1 几种算法的时间复杂度比较 |
改进的算法不仅确保了ECC的安全性, 而且还具有更加优秀的平均计算时间复杂度. 另外也不需要存储NAF码直接进行点乘法, 节省了计算资源.
3 椭圆曲线密码体制与MD5的融合方案提出的方案包含了应用改进的NAF编码算法的椭圆曲线密码体制以及MD5哈希生成算法. 在原有步骤中添加对信息M运用MD5进行128位密码的生成. 具体步骤如图1所示, 首先在进行加密过程中, 将信息M在进行ECC加密的同时, 进行MD5加密得到128位密码. 传输过程由只发送信息M替换为发送信息M以及128位密码. 原有加密过程不变, 而在解密时, 在通过ECC解密得到解密信息M后对信息M进行MD5哈希生成算法. 通过对比解密得到的128位密码与接收到的密码来判断是否接受信息M.
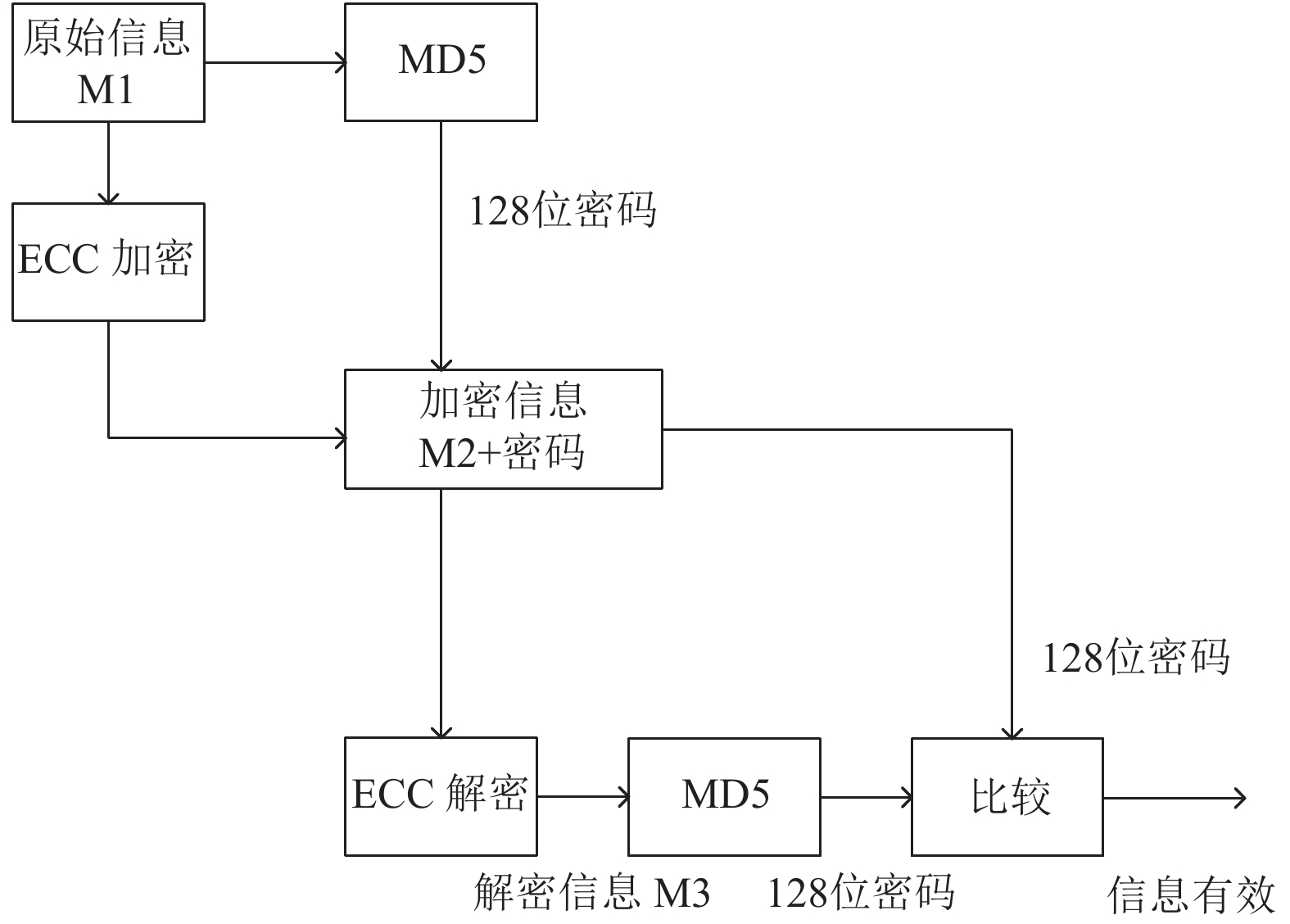
|
图 1 融合方案流程图 |
3.1 安全性分析
改进方案通过MD5算法生成密钥代替了原有的简单步骤, 相对原有数字签名所使用的Hash算法, MD5进一步增强了算法的安全性. 而对于ECC的安全性, 我们通过对ECC与RSA、DSA对比分析. 在目前整数因子分解技术与方法的不断改善, 计算机运行速度的提高的大环境下, RSA加解密安全保障的大整数要求日益变高, 为保证安全性, 就必须不断增加RSA的密钥长度. 目前普遍采用的安全字长为1024位以上, 但密钥长度的增加会直接导致解密速度的降低, 硬件实现也越发困难. 安全性分析如表2所示. 表中MIPS表示每秒执行100万条指令的计算机运行一年. 一般认为破译时间到达1012 MIPS年为安全. 从表中可以知道: 保证安全性的情况下, ECC只需要160密钥长度, 而RSA和DSA则需要1024位. ECC的安全性递增也大大快于RSA和DSA. 攻击有限域上离散对数问题有指数积分法, 而它对椭圆曲线上的离散对数问题并不有效. 对RSA和DSA而言, 均存在指数时间算法, 而对于ECC至今还没有发现指数时间算法. 故在综合比较下ECC的安全性更高、抗攻击性更强.
| 表 2 破译时间比较 |
3.2 融合算法性能评估
本节将对性能进行评估并列出. 对样本文件进行随机抽取进行加解密操作. 以增加文件大小为基础进行不同的实验. 表3表示了有关所有加密文件的信息, 包括文件序号, 存储, 时间, 内存信息和所有加密文件的文件大小. 图2以及图3各自对表格内的内存消耗以及时间消耗给出更为直观的展示. 其中内存消耗表示所需的处理加密算法的主内存量.
| 表 3 文件加密时间, 内存和文件大小 |
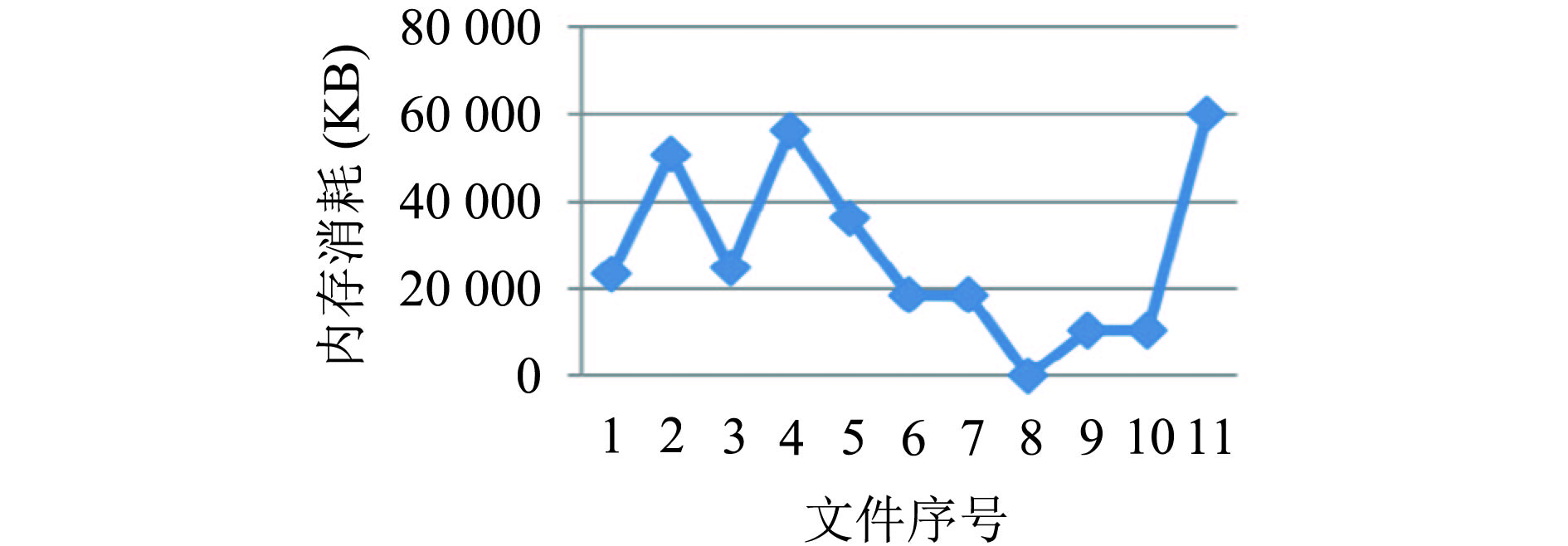
|
图 2 加密内存消耗 |

|
图 3 加密时间消耗 |
表4描述了有关所有解密文件的信息. 解密文件的准确性, 时间, 内存和文件大小给出的信息. 图4对解密的内存消耗进行了展示, 图5则对于解密时间消耗给出直观的展示. 图6中的存储开销是指待加密的原始文件额外的密码的数量. 图7展示了数据解密的准略率, 数据解密准确率是在加密文件解密之后准确恢复的数据量.
| 表 4 文件解密时间, 内存和文件大小 |

|
图 4 解密内存消耗 |

|
图 5 解密时间消耗 |
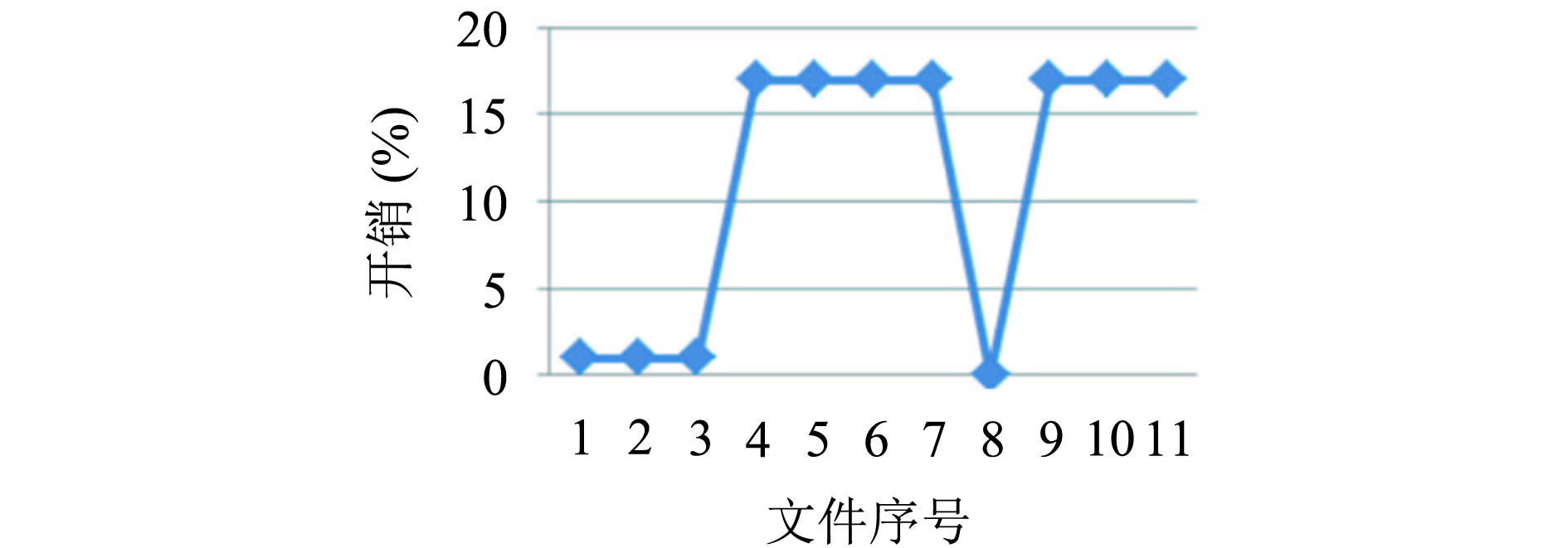
|
图 6 加密存储开销 |

|
图 7 解密准确率 |
分析可得加解密所消耗的时间与内存都在可接受范围内. 由上图分析可得: 存储开销随着原始文件大小增加而增加, 并且总体上开销较少. 结果表明系统在解密过程中可恢复100%的数据. 因而算法在保证安全性的同时, 消耗较少的内存资源以及时间资源从而表明所提出的技术的有效性.
4 结论与展望SET协议是电子支付系统中的关键, 本文通过对SET协议核心技术中的加密算法体制进行研究, 使用椭圆曲线算法取代目前所流行的RSA算法, 从而提高了协议的安全性和工作效率. 同时本文对传统的ECC安全算法进行了比较, 使用一种改进的NAF算法. 对几种加密算法的性能进行了评估内存消耗量和时间消耗. 同时结合了椭圆曲线密码体制与MD5提出了改进性方案, 使用MD5算法代替原有随机生成密钥方法. 比较证明了改进性方案消耗较少的资源并提高了安全性.
| [1] |
Lu S, Smolka SA. Model checking the secure electronic transaction (SET) protocol. Proceedings of the 7th International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems. College Park, MD, USA. 1999. 358–365.
|
| [2] |
SetCo. SET secure electronic transaction specification: Business description. http://www.mastercard.com/set/set.htm.1997.
|
| [3] |
魏来, 杨朵. 一个改进的椭圆曲线密码体制在物联网传输中的研究应用. 信息技术与信息化, 2015(10): 209-212. DOI:10.3969/j.issn.1672-9528.2015.10.079 |
| [4] |
Koblitz N. Elliptic curve cryptosystems. Mathematics of Computation, 1987, 48(177): 203-209. DOI:10.1090/S0025-5718-1987-0866109-5 |
| [5] |
Miller VS. Use of elliptic curves in cryptography. Advances in Cryptology-CRYPTO’85. Santa Barbara, CA, USA. 1986. 417–426.
|
| [6] |
Kobayashi T, Morita H, Kobayashi K, et al. Fast elliptic curve algorithm combining Frobenius map and table reference to adapt to higher characteristic. Advances in Cryptology-EUROCRYPTO’99. Prague, Czech Republic. 1999. 176–189.
|
| [7] |
Wang X, Wang LP, Bai YC, et al. Optimization of elliptic curve cryptography resisting power attack scalar multiplication algorithm in security system on chip. 2015 IEEE 12th International Conference on Ubiquitous Intelligence and Computing and 2015 IEEE 12th International Conference on Autonomic and Trusted Computing and 2015 IEEE 15th International Conference on Scalable Computing and Communications and its Associated Workshops (UIC-ATC-ScalCom). Beijing, China. 2015. 1397–1401.
|
 2018, Vol. 27
2018, Vol. 27



