1 引言

轮询服务系统是一类调度控制模型的代表, 它具有着很好的公平性^[1], 不仅可以对有限的资源进行分配, 而且可以实现资源的共享, 因此它在当前的计算网络中得到了大量的使用. 轮询系统自从被研究和使用以来, 因其控制的灵活性、公平性和实用性, 无论是在工业制造、过程控制, 还是交通调度、设备维修以及通信和计算机网络等领域都得到了广泛应用^[2,3]. 随着研究的不断深入以及应用的不断扩展, 有关轮询系统的研究及应用也将会呈现前所未有的发展空间. 按服务方式的不同, 轮询服务系统可以分为门限、完全以及限定三类^[4]. 而现今大多数对于轮询服务的研究都集中在对称性的轮询服务当中, 对于非对称服务而言, 任意时刻进入网络的数据信息、服务时间和转移时间等参数都是随机可变的, 因此其对应的性能分析具有相当的复杂度, 所以实质性突破相对较难. 但非对称的服务能够更加灵活的运用于实际生活当中, 由于在实际应用中, 经常会有不同类信息或不同类站点, 相应要求在同一种服务策略下, 系统设置的参数需要满足不同类站点自身所需的要求, 这就需要非对称的服务策略. 同时, 无线传感器网络作为下一代的传感器网络, 它在人们的各个领域和生产活动都有着广阔的应用前景. 将轮询服务与无线传感器网络相结合, 可以提高系统的资源利用率, 能够减少数据业务在进行服务时带来的冲突. 如图1所示展现了本文的分析以及设计过程, 主要由理论分析, 仿真实验和无线传感器网络的应用这三部分组成.

2 两队列的非对称模型 2.1 非对称服务的工作条件

(1) 在任意时刻进入队列的数据信息是独立、同分布的Poisson过程^[5,6], 其分布的概率母函数、均值和方差分别为 A i ( z i ) , λ i = A i ' ( 1 ) , δ λ i 2 = A i ' ' ( 1 ) + λ i − λ i 2 , 其中i=1, 2;

(2) 任意队列中每一个数据信息接受的服务时间也是一个独立、同分布的过程, 其概率母函数、均值、方差为 B j ( z j ) , β j = β j ' ( 1 ) . δ β j 2 = A j ' ' ( 1 ) + β j − β j 2 , 其中j=1, 2;

(3) 查询转换时间分布过程的概率母函数、均值和方差各为 R k ( z k ) , γ k = A k ' ( 1 ) , δ γ k 2 = A k ' ' ( 1 ) + γ k − γ k 2 , 其中k=1, 2;

(4) 假设任意一个队列的缓存容量是足够大的, 每个数据信息都可存储在其中, 不会有数据信息丢失的情况发生;

(5) 每个队列中的每个数据信息遵照先到先服务(FCFS)的准则进行服务.

2.2 系统分析定义的变量

u_i(n): 第i队列发送完其所有的数据信息之后, 转向第i+1队列所需的转换时间长度;

v_i(n): 第i队列发送完其中所包含的数据信息所需的时间长度;

μ_j(u_i): 表示在u_i(n)这段时间内加入第j队列的所有数据信息;

η_j(v_i): 表示在v_i(n)这段时间内加入第j队列所有数据信息.

马尔可夫链在 ∑ i = 1 N λ i β i = ∑ i = 1 N ρ i < 1 的条件下达到稳态, 稳态下概率母函数为:

lim n → ∞ P [ ξ i ( n ) = x i ; i ​ = ​ 1 , 2 , ⋅ ⋅ ⋅ , N ] ​ = π i ( x 1 , x 2 , ⋅ ⋅ ⋅ , x i , ⋅ ⋅ ⋅ , x N )

(1)

π i ( x 1 , x 2 , ⋅ ⋅ ⋅ , x i , ⋅ ⋅ ⋅ , x N ) 的概率母函数为:

G i ( z 1 , z 2 , ⋅ ⋅ ⋅ , z i , ⋅ ⋅ ⋅ , z N ) = ∑ x 1 = 0 ∞ ∑ x 2 = 0 ∞ ⋅ ⋅ ⋅ ∑ x i = 0 ∞ ⋅ ⋅ ⋅ ∑ x N = 0 ∞ π i ( x 1 , x 2 , ⋅ ⋅ ⋅ , x i , ⋅ ⋅ ⋅ , x N ) · z 1 x 1 z 2 x 2 ⋅ ⋅ ⋅ z i x i ⋅ ⋅ ⋅ z N x N i = ( 1 , 2 , ⋅ ⋅ ⋅ , N ) .

(2)

2.3 系统的性能分析 2.3.1 两队列的非对称门限服务

由两个队列和一个服务器构成的两队列非对称门限的轮询服务系统^[7]. 其中两个队列采用的服务方式是门限策略. 对于同在一个队列所有的数据信息按照先进先出(FCFS)的方式接受服务. 队列1中, 服务的过程中仍然会有数据信息到达, 而门限服务的方式是将在开始服务之前到达的全部的数据信息服务完成, 至于在服务时段内到达的数据信息会被存储下来, 在下一次轮询时再对其进行服务. 经过一个查询转换时间, 服务器对当前队列2所包含的数据信息进行服务, 同样, 在服务期间到达的数据信息会累积下来, 等下次轮询服务开始时再对其进行访问, 队列2服务完毕之又会经过一个查询转换时间, 再一次转到队列1, 以此来构成了两队列的非对称轮询服务系统. 因此可以得到, 两队列非对称门限服务的在t_n+1时刻有如下关系式:

{ ξ 2 ( n + 1 ) = ξ 2 ( n ) + η 2 ( v 1 ) + μ 2 ( u 1 ) ξ 1 ( n + 1 ) = η 1 ( v 2 ) + μ 1 ( u 2 )

(3)

由此得状态变量在t_n+1时刻的概率母函数为:

G 1 ( z 1 , z 2 ) = R 2 ( A 1 ( z 1 ) A 2 ( z 2 ) ) G 2 ( z 1 , B 2 ( A 1 ( z 1 ) A 2 ( z 2 ) ) )

(4)

G 2 ( z 1 , z 2 ) = R 1 ( A 1 ( z 1 ) A 2 ( z 2 ) ) G 1 ( B 1 ( A 1 ( z 1 ) A 2 ( z 2 ) ) , z 2 )

(5)

g i ( j ) = lim z 1 , z 2 → 1 ∂ G i ( z 1 , z 2 ) ∂ z j i = 1 , 2 , ⋅ ⋅ ⋅ , N ; j = 1 , 2 , ⋅ ⋅ ⋅ , N

(6)

对式(4)和式(5)求一阶偏导可得:

g 1 ( 1 ) = ( γ 1 + γ 2 ) λ 1 1 − ρ 1 − ρ 2

(7)

g 2 ( 2 ) = ( γ 1 + γ 2 ) λ 2 1 − ρ 1 − ρ 2

(8)

其中, g₁(1), g₂(2)分别表示队列1的平均排队队长, 队列2的平均排队队长. 系统的平均查询周期是指同一个站点被系统服务器两次查询访问之间的时间差的统计平均值, 由转换时间以及服务时间组成, 通过计算得到其表达式为:

T θ 1 = T θ 2 = ∑ i = 1 2 γ i 1 − ∑ i = 1 2 ρ i

(9)

2.3.2 两队列非对称完全服务

两队列非对称完全服务的轮询服务系统构成与门限服务相同, 其服务方式是将队列中所有的数据信息全部服务完(包括服务进入的数据信息), 所以我们可以得到其状态变量在t_n+1时刻的概率母函数为:

G 1 ( z 1 , z 2 ) = R 2 ( A 1 ( z 1 ) A 2 ( z 2 ) ) · G 2 ( z 1 , B 2 ( A 1 ( z 1 ) F 2 ( A 1 ( z 1 ) ) ) )

(10)

G 2 ( z 1 , z 2 ) = R 1 ( A 1 ( z 1 ) A 2 ( z 2 ) ) · G 1 ( B 1 ( A 2 ( z 2 ) F 1 ( A 2 ( z 2 ) ) ) , z 2 )

(11)

式中 F i ( z i ) = A i ( B i ( z i F i ( z i ) ) ) , i=1, 2, 表示服务器对任意一个队列, 在任一时隙内到达的数据信息以及在服务期间到达的数据信息使用完全服务的方式所需时间的随机变量的概率母函数^[8].

对式(9), (10)都进行一阶偏导可得

g 1 ( 1 ) = lim z 1 , z 2 → 1 ∂ G 1 ( z 1 , z 2 ) ∂ z 1 = λ 1 ( 1 − ρ 1 ) ( γ 1 + γ 2 ) 1 − ρ 1 − ρ 2

(12)

g 2 ( 2 ) = lim z 1 , z 2 → 1 ∂ G 2 ( z 1 , z 2 ) ∂ z 2 = λ 2 ( 1 − ρ 2 ) ( γ 1 + γ 2 ) 1 − ρ 1 − ρ 2

(13)

平均查询周期为

T θ 1 = T θ 2 = ∑ i = 1 2 γ i 1 − ∑ i = 1 2 ρ i

(14)

式中g₁(1)为队列1的平均排队队长, g₂(2)表示为队列2的平均排队队长, 其中两个队列使用的策略是非对称完全服务.

3 多队列非对称模型

多队列非对称门限服务和多队列非对称完全服务轮询系统, 由一个服务器和多个队列组成, 其中多个队列均采用门限服务的服务策略或均采用完全服务的服务策略进行工作. 对于同在一个队列的所有数据信息也是按照先进先出(FCFS)的策略接受服务^[9]. 当队列i(i=1, 2, …, N)采用门限服务时, 队列i只发送在开始服务之前队列中所包含的数据信息, 对于发送期间到达的数据信息将在下一周期轮询时再发送. 如果队列i使用完全服务, 队列i不仅要发送队列中所有的数据信息, 而且还要发送在服务期间进入的数据信息, 直到队列为空时, 才停止发送, 然后经过一个查询转换时间, 服务器开始对下一队列进行服务.

3.1 多队列非对称门限和完全服务

多队列的非对称门限服务和完全服务在分析的过程中, 其工作条件和系统分析所定义的变量与两队列的服务系统保持一致, 只是在此处分析过程中将两队列的服务机制, 扩展为多对列的服务策略. 因此可以得到多队列非对称门限服务在t_n+1时刻的系统方程为:

{ ξ j ( n + 1 ) = ξ j ( n ) + μ j ( u i ) + η j ( v i ) j ≠ i ξ i ( n + 1 ) = μ i ( u i ) + η i ( v i )

(15)

状态变量在t_n+1时刻的概率母函数为:

G i + 1 ( z 1 , z 2 , ⋯ , z i ⋯ , z N ) = lim n → ∞ E [ ∏ j = 1 N z j ξ j ( n + 1 ) ] = ​ R [ ​ ∏ j = 1 N A ( ​ z j ​ ) ​ ] G i [ ​ z 1 ​ , z 2 ​ , ⋯ , z i − 1 ​ , ​ B ( ​ ∏ j = 1 N A ( ​ z j ​ ) ​ ) , z i + 1 ​ , ⋯ , z N ​ ​ ] i = 1 , 2 , ⋯ , N

(16)

多队列非对称完全服务在t_n+1时刻满足的系统方程为:

{ ξ j ( n + 1 ) = ξ j ( n ) + μ j ( u i ) + η j ( v i ) j ≠ i ξ i ( n + 1 ) = μ i ( u i )

(17)

则状态变量在t_n+1时刻的概率母函数为:

G i + 1 ( z 1 , z 2 , ⋅ ⋅ ⋅ , z i , ⋅ ⋅ ⋅ , z N ) = lim n → ∞ E [ ∏ j = 1 N z j ξ j ( n + 1 ) ] = R [ ∏ j = 1 N A ( z j ) ] G i [ z 1 , z 2 , ⋅ ⋅ ⋅ , z i − 1 , B ( ∏ j = 1 ≠ i N A ( z j ) F ( ∏ j = 1 ≠ i N A ( z j ) ) ) , z i + 1 , ⋅ ⋅ ⋅ , z N ] i = 1 , 2 , ⋅ ⋅ ⋅ , N

(18)

3.2 系统的特性分析

设定在t_n时刻第i队列发送数据信息时, 第j队列缓存区中平均存储的数据信息为:

g i ( j ) = lim z 1 , z 2 , ⋅ ⋅ ⋅ , z i , ⋅ ⋅ ⋅ , z N → 1 ∂ G i ( z 1 , z 2 , ⋅ ⋅ ⋅ , z i , ⋅ ⋅ ⋅ , z N ) ∂ z j

(19)

计算得到第i队列使用非对称门限服务时的平均排队队长为^[10]:

g i ( i ) = λ i ∑ j = 1 N γ j 1 − ∑ j = 1 N λ j β j i , j = 1 , 2 , ⋅ ⋅ ⋅ , N ;

(20)

计算得到第i队列在接受非对称完全服务时的平均排队队长为:

g i ( i ) = λ i ( 1 − λ i β i ) ∑ j = 1 N γ j 1 − ∑ j = 1 N λ j β j i , j = 1 , 2 , ⋅ ⋅ ⋅ , N ;

(21)

通过理论计算得到多队列非对称门限服务和完全服务系统的平均查询周期的表达式均为:

T θ i = E [ θ i ] = ∑ i = 1 N γ i 1 − ∑ i = 1 N λ i β i

(22)

4 仿真实验及性能分析

根据以上所建立的非对称门限、完全服务的系统模型, 并基于下面的工作条件进行数值计算和仿真实验．

(1) 各队列的参数都遵从相同的概率分布, 但并不具有对称性;

(2) 任一时隙内进入各队列的数据信息都满足Poisson分布;

(3) 轮询系统满足 ∑ i = 1 N λ i β i = ∑ i = 1 N ρ i < 1 稳态条件^[9].

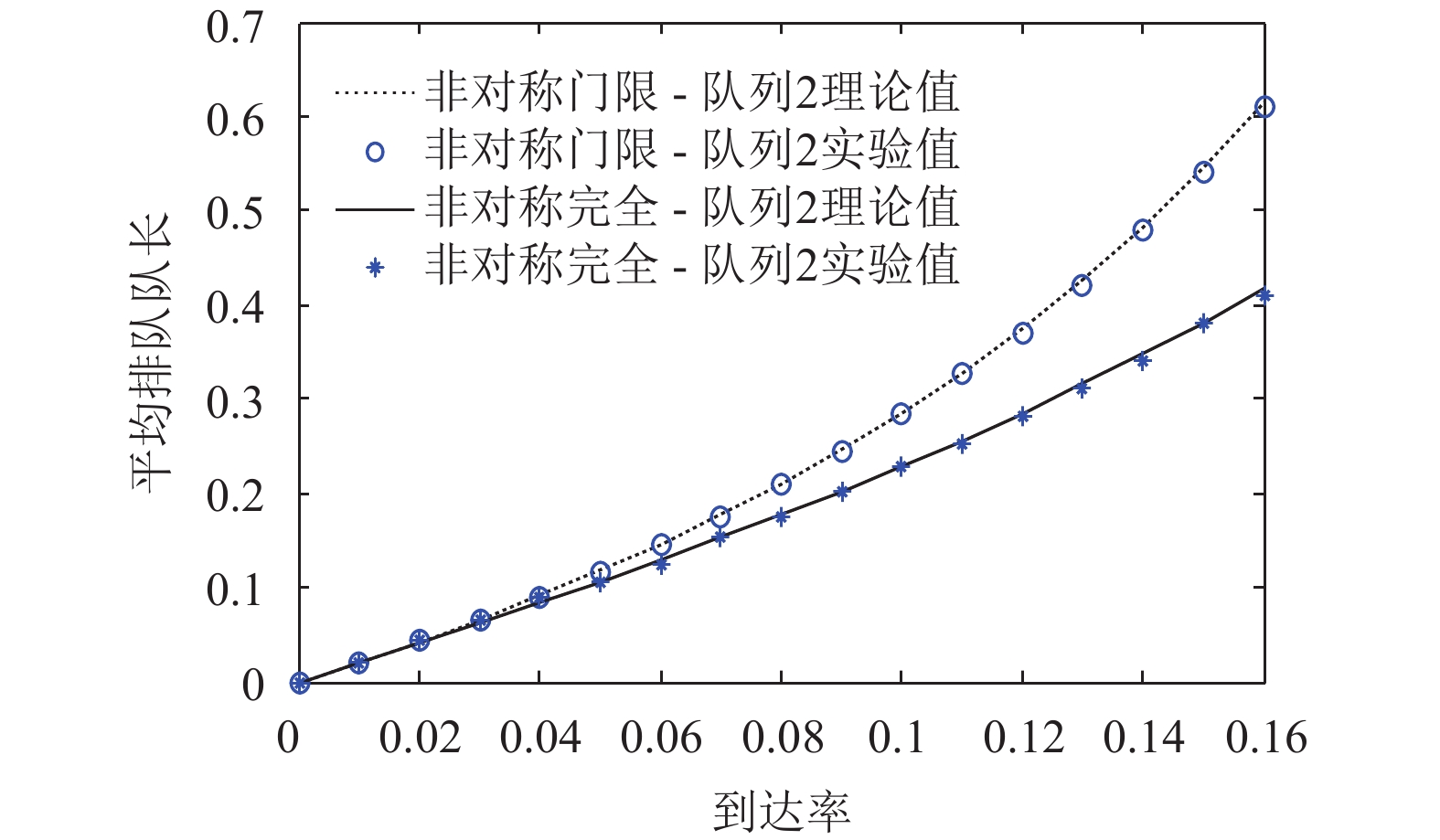
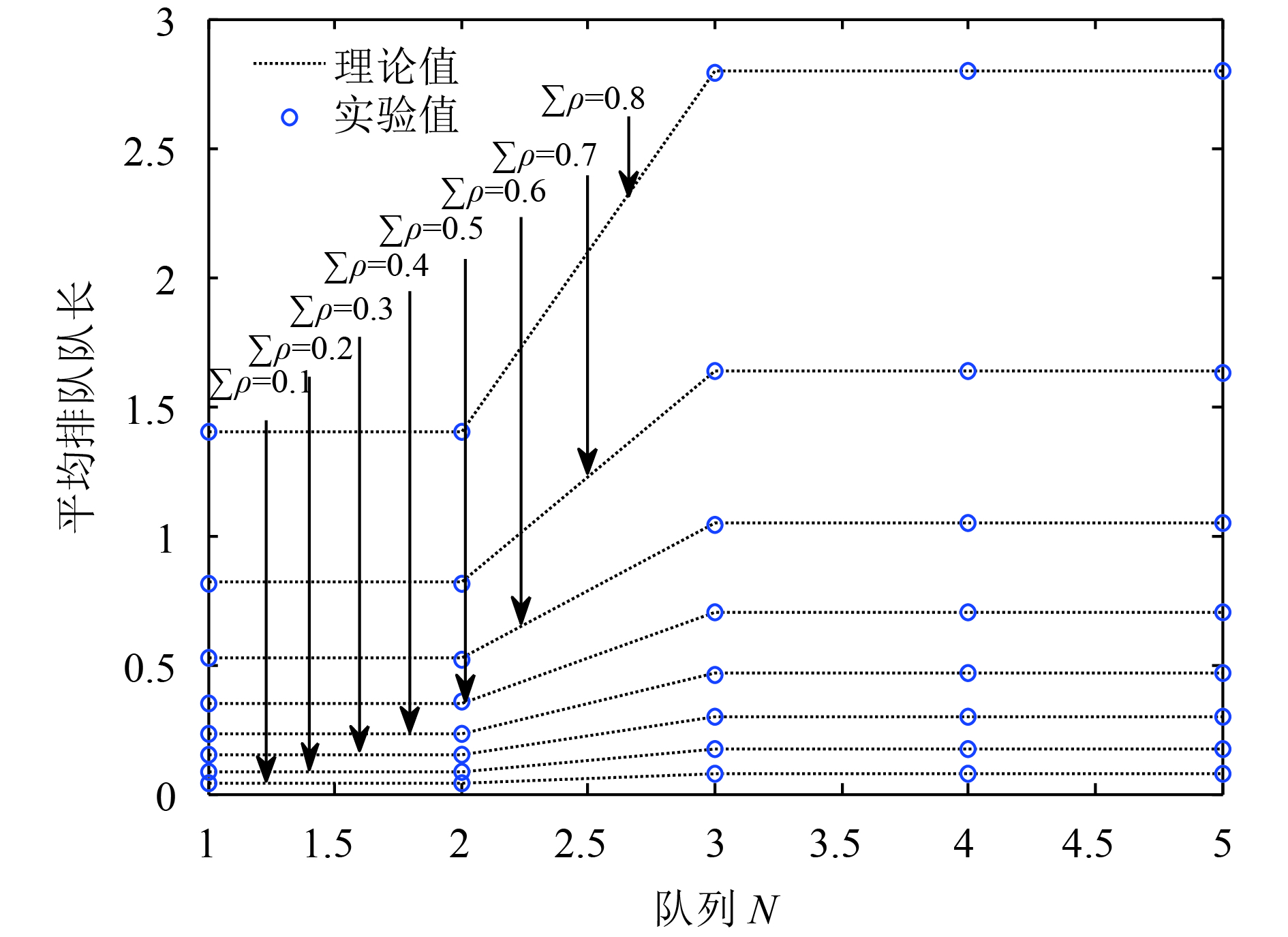
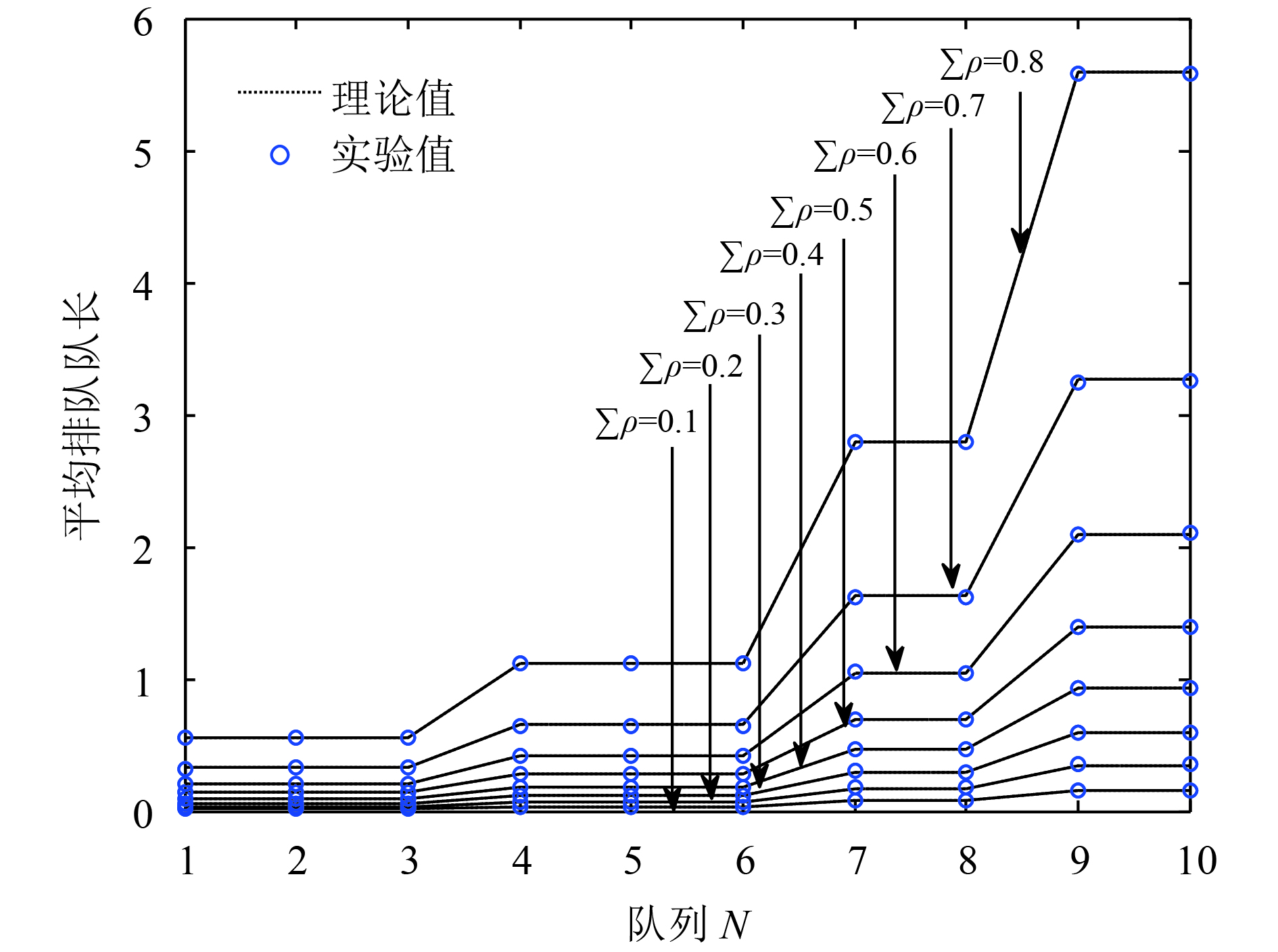
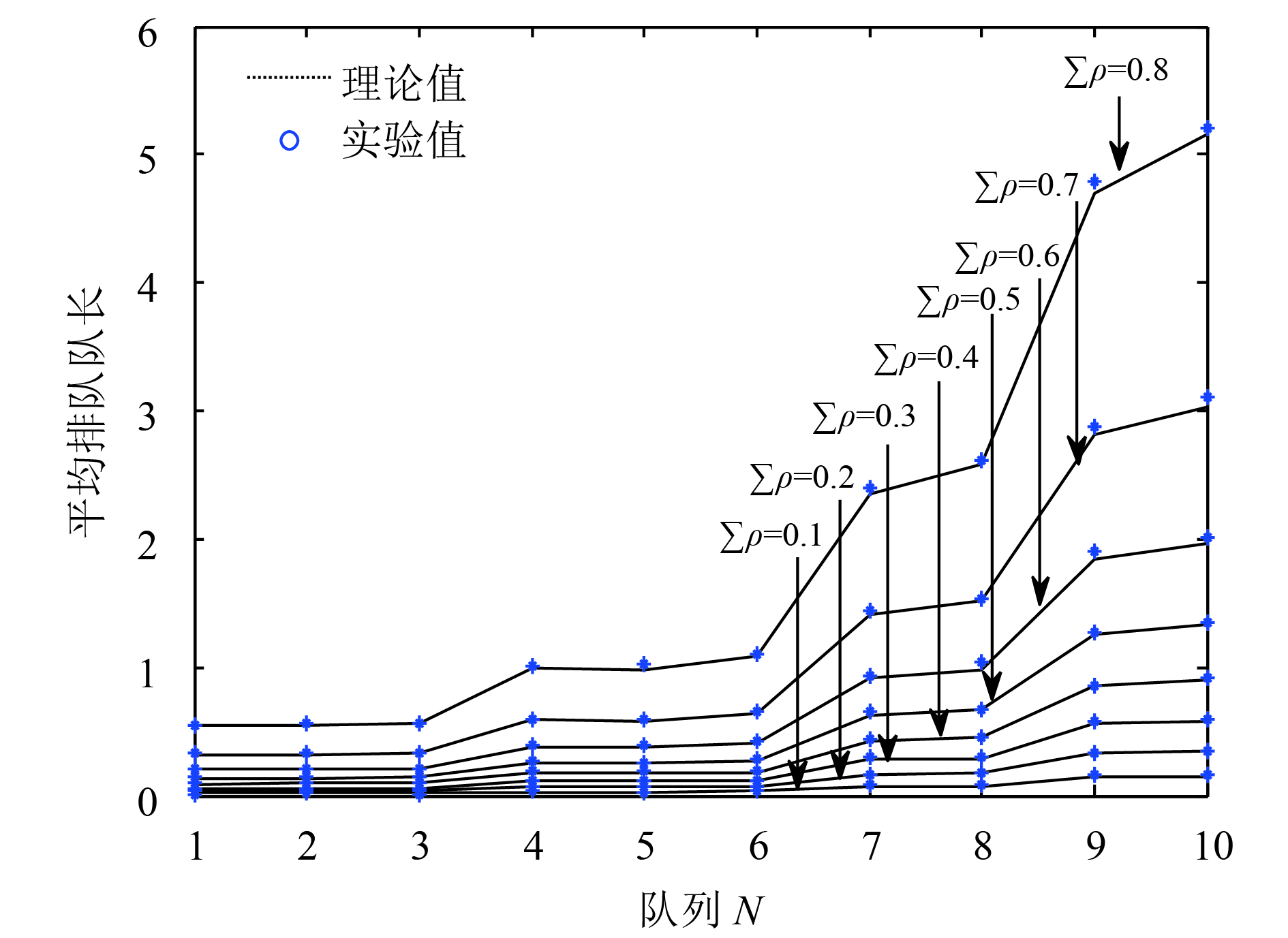
从图2和图3中, 我们可以看出无论是非对称门限服务还是还是非对称完全服务, 随着到达率的增大, 它们的平均排队队长都是随之而增大的. 但是非对称完全服务的平均排队队长小于非对称门限服务的队长, 到达率越大, 这种关系更加明显. 从图4中, 可以观察到, 两队列的非对称门限、完全服务的平均排队队长随着服务率的增大, 它们的平均排队队长也在变大, 同时也满足非对称门限服务的平均排队队长大于非对称完全服务的变化关系. 图5至图8为多队列非对称门限、完全服务系统性能特性的理论值计算与实验仿真的关系图, 当选取统计循环次数足够大时, 信息分组的平均排队队长的实验值与理论值结果保持一致, 误差较小. 对同一系统而言, 两种非对称服务, 受负载的影响是比较明显的, 尤其是当负载变大时, 平均排队队长会急剧变大, 从式(20)和式(21)中我们可以看出负载与队长呈一个正比关系, 所以图形的变化情况与理论推导是相一致的. 与此同时, 从图5与图6, 两种非对称服务在队列数N=5时平均排队队长随负载变化的关系曲线, 图7与图8, 两种服务在队列数N=10时平均排队队长随负载变化的关系曲线, 都满足在同一负载下, 非对称门限服务的平均排队队长大于非对称完全服务的平均排队队长, 随着负载的变大这种关系更加明显, 而且无论队列数是多还是少, 这种关系是一直存在的. 所以就其平均排队队长而言, 非对称完全服务是优越于非对称门限服务的, 然而从公平性来看非对称门限服务要比非对称的完全服务好. 综上, 也给在无线传感器网络中, 选择一种合适的轮询服务提供了参考, 例如, 当数据业务量或者是网络流量较大时, 非对称完全服务的公平性相对较差, 业务的服务质量得不到很好的保障, 此时我们应当选择非对称门限的机制来进行服务.

5 无线传感器网络中轮询服务的设计

在无线传感器网络中实现非对称的轮询服务, 我们将选择由加州伯克利分校根据无线传感器网络的特点专门为其设计并实现的Tiny0S嵌入式操作系统作为软件平台^[10,11]. 在硬件平台的选择上, 我们选择cc2538cb来作为传感器节点. 测试过程中将设定一个节点作为汇聚节点来充当服务器, 负责对其他多个子节点进行服务. 每个子节点在未接受服务之前, 一直处于睡眠侦听的状态, 当接收到来自于服务器的信标帧时, 就会被唤醒, 此时就会选择门限服务或完全服务的方式对对数据包进行发送. 在无线传感器网络的应用中, 我们可以根据此前分析得到两种非对称服务的性能差异去选择一种合适的服务, 因为在数据业务量较大时, 完全服务系统的公平性和服务质量较差, 此时就可以去选择门限服务的方式.

节点程序主要用到的组件有main组件, led灯组件LedC, 时钟组件TimeC, IPStackC组件, 还有StaticIPAddressTosIdC和UdpSocket组件, 组件之间的连接关系如下图9所示.

6 结论

本文以两对列的非对称服务模型作为基垫, 使用嵌入式马尔可夫链和概率母函数的方法对非对称性门限服务和非对称完全服务控制技术建立了模型^[12,13], 对两种非对称服务的特性进行了比较, 得到了两队列非对称的轮询服务系统中, 随着到达率和服务率的增大完全服务的平均排队队长小于门限服务的平均排队队长的变化关系. 同时, 在此基础之上, 将两种非对称服务的分析拓展到多个队列, 随之分析了两种多对列的性能特性, 通过理论计算和实验仿真证明了两种多队列非对称服务模型的有效性. 与对称的轮询服务相比较, 对称性的轮询系统各参数是固定不变的, 所以存在一定的局限性, 但是在非对称的轮询服务中, 其系统参数是可变化的, 也因此其能够更好的满足实际应用的需求. 在未来的工作中, 我们将对非对称的轮询服务在无线传感器网络中的应用中进行深入的研究, 并可以根据本文分析得到的两种非对称服务的性能差异, 针对应用实际的需要动态的选择一种更为适合的轮询服务.