随着科学技术的迅猛发展, 计算机在人类日常的学习、生活、工作中扮演着越来越重要的角色. 而键盘作为计算机的主要输入工具, 其重要性不言而喻. 此外, 诸如机房、网吧等公共场所使用计算机人群众多且复杂, 实时地对计算机键盘实施异常检测可以减轻不必要的经济损失, 同时亦可提高用户的满意度, 因此对键盘的异常检测十分具有现实意义.
异常检测是基于行为的检测, 即根据使用者的行为或者资源的使用状况来判断异常情况是否发生, 因为我们每个人都有不同的生物特征, 即每个人对键盘的敲击习惯都是不同的, 如击键的轻重, 快慢等, 所以我们可以选用它作为识别用户的信息源[1]. 常用的生物技术有语音识别技术, 指纹识别, 人脸识别, 击键认证. 本文采用的就是击键认证, 由每个人的击键行为, 在键盘上产生的按键时间序列, 通过一些特征变换衍生, 构建出识别模型, 用来对键盘的异常情况进行识别. 击键特征是一种能够反映用户行为的动态特征, 通常情况下无需借助其他设备我们便可以捕获个人的击键特征. 我们通过训练出的模型和定义异常指数, 检测出键盘是否发生异常.
支持向量机方法在检测方面已经应用于多个领域, 如: 冯慧玲等[2]提出的基于拉普拉斯分值和超球支持向量机的轴承故障诊断方法设计; 郝英等[3]提出的基于支持向量机的民航发动机故障检测研究; 以及张馄等[4]提出的基于支持向量机的异常入侵检测系统和郭月玲[5]对支持向量机在语音识别中的应用研究. 目前, 对于键盘的异常检测方法并不多, 考虑到超球支持向量机适合处理非线性, 多维模式的小样本数据识别问题, 且在处理不均衡样本中有独特的优势[6], 而人们的击键时间序列正是非线性, 不均衡, 小样本数据, 所以本文提出了一种基于超球支持向量机的键盘异常检测方法.
1 超球支持向量机模型及粒子群算法优化模型参数 1.1 超球支持向量机模型[7–10]支持向量机是以统计学习理论为基础的一种新的机器学习算法, 它具有简洁的数学形式、标准快捷的训练方法, 基本思想是通过一个非线性变换将输入空间变换到一个高维特征空间, 然后构造平面对样本进行划分. 支持向量机具有更坚实的理论基础、更强的泛化能力, 性能也更加优异, 且适合处理小样本多特征的数据, 因此成为主流的机器学习算法之一. 目前, 常用的异常检测的支持向量机模型有两种, 其中一种是就是本文应用的超球模型, 它是Tax提出来的, 它比另一种超平面模型具有更大的优势. 超平面模型的不足在于特征空间内的原点被先验地认为是异常样本区域的中心, 然后寻找超平面使得正常样本区域尽量远离该中心. 且超平面只是将两类样本分开, 由于超平面把空间一分为二, 两边的地位都是相等的, 对于第三类样本无法做出相应的处理. 而超球模型不仅可以处理第三类样本, 还具有训练速度快, 检测效率高的优点. 通过控制超球的大小和范围, 使超球的含义不仅仅是分开两类, 而且还有把球里面的样本尽量包“牢”和包“纯”, 拒绝其它类样本的进入.
Tax提出的超球模型思路如下: 在样本特征空间内寻找一个中心为a, 半径为R的超球, 正常样本点位于超球内, 异常点位于超球之外, 所谓异常点就是比如我们要将10 000个样本进行分类, 我们可以找到一个分类面将9999个样本正确分类, 但只有一个样本错误分类, 那我们就不需要不断调整分类面直到将10 000个样本完全正确分类了. 优化目标是超球体积尽量小, 同时位于超球外的样本点也要尽量少. 该模型目标函数如下:
| $\begin{array}{c}\min \left( {{R^2} + C\sum\limits_i {{\xi _i}} } \right)\;\;{{s.t.}}\;\;{({x_i} - a)^{{T}}}({x_i} - a) \le {R^2} + {\xi _i}\;\;{\xi _i} \ge 0\end{array}$ | (1) |
其中,
| $\begin{align}L(R,a,{\alpha _i},{\xi _i})& = {R^2} + C\sum\limits_i {{\xi _i}} - \sum\limits_i {{\gamma _i}} {\xi _i} \\&- \sum\limits_i {{\alpha _i}} [{R^2} + {\xi _i} - {({x_i} - {{a}})^{{T}}}({x_i} - {{a}})] \end{align}$ | (2) |
其中,
| $\left\{ \begin{array}{l}\sum\limits_i {{\alpha _i} = 1} \\a = \sum\limits_i {{\alpha _i}{x_i}} \\C = {\alpha _i} + {\gamma _i}\end{array} \right.$ | (3) |
将式(3)带入Lagrange函数, 可得到:
| $W(\alpha ) = \sum\limits_i {{\alpha _i}} ({x_i},{x_i}) - \sum\limits_{i,j} {{\alpha _i}} {\alpha _j}({x_i},{x_j})$ | (4) |
其中,
| $W(\alpha ) = \sum\limits_i {{\alpha _i}} k({x_i},{x_i}) - \sum\limits_{i,j} {{\alpha _i}} {\alpha _j}k({x_i},{x_i})$ | (5) |
其中,
| $s.t.\left\{ \begin{array}{l}\sum\limits_i {{\alpha _i} = 1} \\0 \le {\alpha _i} \le C\end{array} \right.$ | (6) |
对式(5)进行优化求出
| ${\left\| {z - a} \right\|^2} = k(z,z) - 2\sum\limits_i {k(z,{x_i})} + \sum\limits_{i,j} {{\alpha _i}} {\alpha _j}k({x_i},{x_j}) \ge {R^2}$ | (7) |
则判断z为异常点.
本文选用径向基核函数作为HSSVM核函数, 公式如下:
| $k({x_i},{x_j}) = \exp ( - {\left\| {{x_i} - {x_j}} \right\|^2}/{\sigma ^2})$ | (8) |
其中xi, xj分别为第i, j个样本,
粒子群算法(PSO)是一种迭代寻优方法[11]. 该算法来源于对鸟群捕食行为的研究, 具有智能搜索的性质, 同时, 它利用速度与位置的更新策略, 致使算法简单易操作. 算法可以描述为: 设在n维空间中分布一个粒子种群, 该种群由m个粒子组成, 每个粒子的位置对应求解问题中一个潜在解, 每个粒子同时还具备向其它粒子飞行的速度, 该速度决定它们飞行的方向和距离. 首先随机产生一组粒子的初始位置和速度, 根据预定的适应度函数计算每个粒子当前位置的适应度值, 此时, 各个粒子本身的最优解称为个体极值, 整个种群的最优解称为全局极值. 然后, 粒子按公式(9)、(10)通过
实现个体在自由空间的寻优.
| $V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{r_1}(pBest_{id}^k - X_{id}^k)+ {c_2}{r_2}(gBest_{gd}^k - X_{id}^k)$ | (9) |
| $X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1}$ | (10) |
式中
| $\omega = \left\{ \begin{array}{l}{\omega _{\min }} - \displaystyle\frac{{({\omega _{\max }} - {\omega _{\min }})(f - {f_{\min }})}}{{{f_{{avg}}} - {f_{\min }}}},f < {f_{{avg}}}\\{\omega _{\min }}, \quad\quad\quad\text{其他}\end{array} \right.$ | (11) |
其中,
| $\left\{ \begin{array}{l}{c_1} = {c_{1ini}} + ({c_{1fin}} - {c_{1ini}})(t/{T_{\max }})\\{c_2} = {c_{2ini}} + ({c_{2fin}} - {c_{2ini}})(t/{T_{\max }})\end{array} \right.$ | (12) |
其中,
由于超球支持向量机中模型参数对分类结果有较大影响[13], 本文利用粒子群优化算法对超球体支持向量机中的参数进行优化, 其整个建模流程如下;
1) 读入训练样本集;
2) 进行初始化包括种群规模
3) 定义PSO的适应度函数来进行粒子的适应度值计算和评估, 选取最为常用的均方误差(MSE)作为为适应度函数. 公式如(13)所示:
| ${f_{{MSE}}} = \left( {\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } \right)/n$ | (13) |
式中xi为估计值, yi为实际值;
4) 根据粒子的适应值来更新粒子本身和群体所对应的最佳适应值, 根据公式对粒子的速度, 位置, 学习因子
5) 如未满足结束条件或达到最大迭代次数, 返回步骤3)否则输出最优参数值;
6) 把最优参数值代入超球支持向量机得到键盘异常模型, 并用测试样本集对模型检测准确率进行验证.
2 基于IPSO-HSSVM键盘异常检测模型构建 2.1 模型样本数据采集及样本参数指标构建在用户整个敲击键盘的过程中, 用户实际上完成了一套连续按下弹起行为, 每个这样的按键行为都是按键被输入进了电脑[14]. 一个按键被电脑识别, 一共会产生两次的时间记录, 一次是按键按下(DOWN)的时间, 另一次则是按键弹开(UP)的时间. Windows系统是建立在事件驱动的机制上的, 说穿了就是整个系统都是通过消息的传递来实现的. 而钩子是Windows系统中非常重要的系统接口, 它的种类是有很多种, 每一种钩子都可以截获并处理相应的消息, 得到此消息的控制权, 此时在钩子函数中就可以对截获的消息进行加工处理, 甚至可以强制结束消息的传递, 用它可以截获并处理送给其他应用程序的消息, 来完成普通应用程序难以实现的功能. 所以, 本文在Windows操作系统中, 通过开发的钩子(hook)程序捕获键盘的击键消息, 并记录下每个键按下(DOWN)和弹开(UP)的时间间隔以及任意两个键之间的时间间隔(即前一个键弹开(UP)和下一个键按下(DOWN)的时间间隔).
键盘的异常特征是可以通过按键之间的时间序列来较好判断的. 因为模型算法是来检测现实情况下的键盘异常情况的, 所以训练样本的质量尤为关键, 必须真实有效, 能够反映用户习惯的数据. 实验数据来源一部分是让用户在正常情况下连续打印了课外阅读中一篇完整的文章, 另一部分是让一位不太熟悉计算机的中年人打印同样一篇文章并加入一些人为模拟出的异常数据组合起来作为异常样本, 因为各个按键之间的频率是不一样的, 本文从采集的数据样本中找出按键频率较高的几种数据作为样本, 通过观察采集的数据和参考国内外相关文献[15,16], 我们发现其中a键按下和弹开, a键弹开之后再按下n键, a键弹开之后再按下i键, i键弹开之后再按下a键, h键弹开之后再按下a键出现的频率较高, 所以采集的数据样本较多, 本文中把其时间间隔分别记为Taa, Tan, Tai, Tia, Tha, 单位为秒. 从而组成一组样本点数据x(Taa, Tan, Tai, Tia, Tha), 包含用户敲击a键的5个击键特征作为指标. 通过收集和整理, 最终选取了230组数据, 其中100组数据作为训练集, 其余130组数据作为训练集(包含100组正常数据和30组异常数据). 钩子程序是在Visual Stdio 2010环境中开发的, 表1是采集数据时的部分整理数据.
| 表 1 采集数据时的部分整理数据 |
训练样本集即是对
HSSVM键盘异常检测模型主要由3部分构成:
1) 数据采集整理部分, 由每个人的击键行为, 利用钩子(hook)程序采集在键盘上产生的按键时间序列, 从中选出能反映人们击键行为的按键时间间隔作为击键特征, 组成训练集和测试集, 以适用于实验分析需要.
2) IPSO算法部分, 通过粒子动态更新速度, 位置, 学习因子和惯性权重, 并根据训练集计算适应度值, 找到最佳的一组搜索参数
3) HSSVM算法部分, 通过训练集的监督学习, 建立对应HSSVM键盘异常检测的分类器, 再使用测试集验证模型检测准确率.
算法流程图如图1所示.
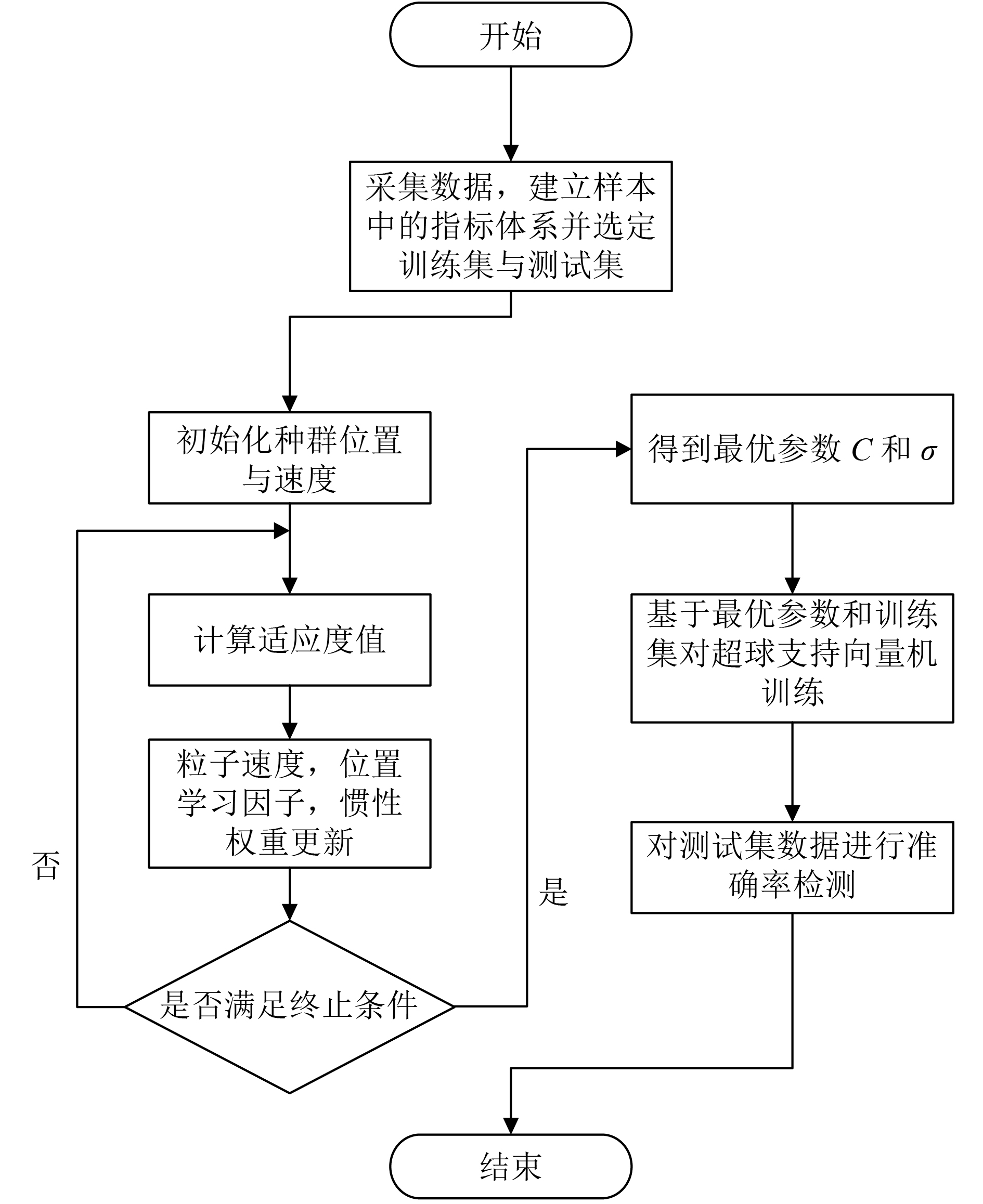
|
图 1 HSSVM模型流程 |
3 结果分析
实验相关参数设置: 粒子种群规模
为进一步对键盘异常状态程度进行衡量, 且方便对模型输出效果的直观表示, 根据公式(7)改写定义一个异常指数NI形式如下:
| $NI = {\left\| {{{z - }}a} \right\|^2}/{R^2}$ | (12) |
其中z为被测样本, a为超球中心, R为超球半径, 若NI<1, 则判z为正常样本; 若NI>1, 则判z为故障样本, 且NI越大, 表明故障越严重或者发生异常的可能性越大. 选用测试集中100组正常样本和30组异常样本作为测试样本来检测模型的输出情况, 并和没有经过改进的粒子群算法优化过参数的HSSVM相比较, 检测结果统计如表2所示.

|
图 2 两种粒子群算法的迭代过程对比 |
| 表 2 参数优化前后模型检测准确率对比 |

|
图 3 正常样本集异常指数 |
从图3中可以看出, 选取的100个正常样本, 采用IPSO-HSSVM模型时异常指数大于1的有7个, 所以误判个数为7个, 准确率为93%, 而未优化参数前采用HSSVM模型时异常指数大于1的有15个, 准确率为85%, 从图4中我们可以看出, 30个异常样本中, 采用IPSO-HSSVM模型时异常指数小于1的有1个, 所以误判个数为1个, 准确率为96.7%, 而未优化参数前采用HSSVM模型时异常指数大于1的有4个, 准确率为87%, 整体测试样本采用IPSO-HSSVM模型时误判8个, 准确率为93%, 而未优化参数前采用HSSVM模型时误判样本19个, 准确率只为85%, 对比可知, IPSO-HSSVM的测试样本准确率均高于HSSVM, 验证了IPSO-HSSVM用于键盘异常检测是有效可行的, 且较为理想的.

|
图 4 异常样本集的异常指数 |
4 总结
异常检测是基于行为的检测, 本文根据人们的击键行为提取到击键特征, 在采集按键的时间序列时, 采用的是键盘钩子程序, 它可以在windows平台捕获键盘动作, 将其挂入系统, 通过对采集的大量数据进行观察比较整理, 组成能够反映击键行为特征的数据作为训练集和测试集, 以满足实验要求. 由于模型参数的选择对实验结果的影响是非常大, 所以模型参数的选取就显得尤为重要, 本文采用IPSO进行寻优, 根据实验得到一组最好的模型参数, 带入此模型进行训练. 实验结果表明: IPSO-HSSVM模型用于键盘异常检测模型有效可行, 检测准确率达到93.8%, 在理想范围之内, 并和参数优化前相比较, 测试样本判断准确率均有所提高.
| [1] |
齐晋. 基于支持向量机的击键辅助认证系统[硕士学位论文]. 成都: 西南财经大学, 2014.
|
| [2] |
冯慧玲, 常国权, 孔娟. 基于拉普拉斯分值和超球支持向量机的轴承故障诊断方法设计. 计算机测量与控制, 2015, 23(4): 1102-1105. |
| [3] |
郝英, 孙健国, 杨国庆, 等. 基于支持向量机的民航发动机故障检测研究. 航空学报, 2005, 26(4): 434-438. |
| [4] |
张琨, 许满武, 刘凤玉, 等. 基于支持向量机的异常入侵检测系统. 计算机工程, 2004, 30(18): 43-45. DOI:10.3969/j.issn.1000-3428.2004.18.017 |
| [5] |
郭月玲. 支持向量机在语音识别中的应用研究[硕士学位论文]. 太原: 太原理工大学, 2009.
|
| [6] |
吴小豪, 张跃文, 孙培廷, 等. 基于超球支持向量机的船舶高温淡水系统状态评估. 船舶工程, 2017, 39(2): 49-52, 93. |
| [7] |
Tax DMJ, Duin RPW. Support vector data description. Machine Learning, 2004, 54(1): 45-66. DOI:10.1023/B:MACH.0000008084.60811.49 |
| [8] |
Tax DMJ, Duin RPW. Support vector domain description. Pattern Recognition Letters, 1999, 20(11–13): 1191-1199. DOI:10.1016/S0167-8655(99)00087-2 |
| [9] |
龙熙华, 张兵, 高凯. 超球体支持向量机在测井岩性识别中的应用. 数学的实践与认识, 2013, 43(18): 110-115. DOI:10.3969/j.issn.1000-0984.2013.18.015 |
| [10] |
刘其琛, 穆炜炜. 最小二乘支持向量机的核函数及参数选择算法研究. 电脑知识与技术, 2015, 11(19): 160-162. |
| [11] |
黄太安, 生佳根, 徐红洋, 等. 一种改进的简化粒子群算法. 计算机仿真, 2013, 30(2): 327-330, 335. |
| [12] |
吴华伟, 陈特放, 胡春凯, 等. 一种改进的约束优化粒子群算法. 计算机应用研究, 2012, 29(3): 859-861. |
| [13] |
王启明, 郑均辉. 基于支持向量机的网络参数模型研究. 现代电子技术, 2015, 38(12): 23-24. |
| [14] |
高艳, 管晓宏, 孙国基, 等. 基于实时击键序列的主机入侵检测. 计算机学报, 2004, 27(3): 396-401. |
| [15] |
Fu MY, Tian Y, Wu F. Step-wise support vector machines for classification of overlapping samples. Neurocomputing, 2015, 155: 159-166. DOI:10.1016/j.neucom.2014.12.035 |
| [16] |
李晨, 张功萱, 岳宝玲, 等. 一种基于条件随机场的击键特征身份鉴别方法. 计算机应用研究, 2014, 31(7): 2112-2115. |
 2018, Vol. 27
2018, Vol. 27



