2. 西安理工大学 计算机科学与工程学院, 西安 710054
2. School of Computer Science and Engineering, Xi’an University of Technology, Xi’an 710054, China
近几年我国煤炭产量不断增大, 但发生的煤矿事故也较为严重, 死亡人数总量是世界上其他产煤国家死亡总数的3倍, 远远超过世界其他产煤国家煤矿事故死亡总数, 此外全国每年还有十几万的事故伤残人员. 据统计, “十一五”期间, 全国煤矿发生特别重大水害事故26起, 平均每年发生5起, 共死亡506人. 种种事实数据表明, 目前我国煤炭企业安全生产形势较为严峻, 煤矿突水预测已成为煤矿安全生产亟需解决的问题, 具有非常重要的现实意义.
目前, 煤矿突水预测方法主要分为两大类: 即基于突水机理预测法和数学与计算机模型预测法. 基于突水机理预测法的缺陷在于目前的研究大多从力学角度出发, 通过试验或数值模拟建立力学模型, 因不能全面考虑突水影响因素, 建立的模型并不能真实反映实际情况, 例如实际中煤层底板很难满足薄板理论的基本条件(厚宽比小于1/5~1/7); 数学与计算机模型预测方法通常采用突水指数法, 如突水概率指数法[1], 层次分析法[2], 聚类分析法[3], 脆弱性指数法[4], Logist二元回归分析法[5], Probit回归模型[6], 事故树分析法[7]以及神经网络预测法[8–11]等等. 建立在数学方法上的突水预测方法, 都是基于某种理论并对其进行简化建立预测模型, 使得矿井突水预测方法得到一定程度提高, 但模型无法保证所有突水样本的正判(即突水样本100%的正判率)[12–14]. 事实上一次突水事故误判可能造成无法估量的经济损失, 为此本文基于煤矿突水预测需求、样本数据非均衡、空间交错以及不同样本误判后果的巨大差别, 提出面向非均衡样本集的煤矿突水预测模型, 以不突水样本误判率最小为代价, 力求突水样本100%的判别准确率. 重点研究基分类器的构建算法、性能评判指标、基于分类规则与样本贴近度的权重分析以及集成学习算法, 实验表明该算法在保证整体预测准确率前提下, 突水样本正判率100%, 模型测试性能良好, 与Bagging算法相比具有较快的收敛速度及较高的预测准确率.
2 煤矿突水影响因素及数据集样本特征分析如上所述, 目前的研究忽视了对矿井工程地质条件和模型的基础研究, 没能查清和分析工程地质单元特征、岩体结构、地质构造、地应力情况、水文地质条件及开采条件对突水的作用. 针对这个问题, 作者通过参阅文献和在煤炭部西安分院、陕西煤炭研究所部分专家的帮助下, 依据煤矿的构造条件、岩性组合条件、含水层条件、开采条件及突水征兆5个方面确定了影响煤矿突水的22个因素(数据结构如表1).
煤矿突水机理具有多样性, 是指在不同的地质及水文地质条件下, 采用破坏或水压破坏表现出不同的空间组合特征, 突水机理的多样性反映了地质及水文地质条件的变化, 煤矿突水是否突水受制于诸多因素的综合影响. 尽管如此, 但根据文献[2], 施工经验及《矿区水文地质工程地质勘查规范》, 在诸多因素中, 断层充水X5和含水层水压X12对煤矿是否发生突水影响最大.
| 表 1 煤矿突水预测样本数据结构 |
毫无疑问, 相对于正常煤矿生产, 发生突水毕竟是小概率事件, 通常收集的煤矿突水样本集中, 不突水样本个数远大于突水样本数目, 加之各煤矿地质条件、施工条件的综合影响, 样本数据集具有如下特征:
(1)样本种类比例呈现非均衡状态, 不突水样本个数远大于突水样本数目. 突水样本数目少, 空间分布相对集中, 不突水样本数目较大, 相对比较分散.
(2)由于地质条件、施工条件及偶然因素的影响, 导致样本数据发生冲突, 例如22个影响因素的数据大致相近, 大部分样本数据标签为“不突水”, 个别样本标签为“突水”.
(3)类别不同, 误判的严重性差别很大. “不突水”误判为“突水”无非是提醒施工人员加强防范, “虚惊一场”; 但“突水”误判为“不突水”那将是“千古罪人”.
对于传统的预测方法、神经网络、多元回归及支持向量机, 非均衡数据集可能导致训练模型包含过多的“不突水”样本信息, 但只有少量“突水”样本信息, 拟合过度, 尽管模型整体预测率较高(对大量不突水样本预测准率较高), 但对“突水”样本预测准确率较低. 加之上述特征2提到的样本冲突问题, 增加了传统预测方法对“突水”样本正确预测的难度.
近年来集成学习是近年来机器学习领域中的研究热点之一. 由于可以取数量大致相当、类别不同的样本构建基分类器, 以及在众多分类器中依据用户需求选择性能良好的分类器, 因此集成学习成为最有希望解决非均衡样本集准确预测的方法.
3 基于集成分类的煤矿突水预测模型集成学习经典的两个算法是Bagging (Bootstrap Aggregating)和AdaBoost, 其工作原理都是首先构建若干个基分类器, 然后对各基分类器的预测结果进行综合分析, 最终确定预测结果, 从而提高分类预测的准确率. 由于可以取不同类别样本数量大致相当构建基分类器, 以及在众多分类器中依据用户需求选择合适的分类器, 因此集成学习成为最有希望解决非均衡样本集准确预测的方法.
3.1 基分类器的构建从理论上讲分类器的选择是任意的, 但由于样本向量数据中通常存在数值型变量、类别及次序等多种变量, 因此经典的Bagging和AdaBoost算法中绝大多数都采用决策树分类器. 考虑到煤炭突水影响因素大多为连续性数值型变量, 采用决策树处理这类变量时需要分段离散化处理, 分段越多, 决策树节点越多, 预测精度较高, 但增加了计算量. 相反分段越少, 决策树节点少, 预测精度不能保证. 同时考虑到煤矿突水预测隶属分类预测, 本文首先识别出边界样本, 选择部分别界样本构建基分类集、采用类似聚类的距离判别法构建煤矿突水的基分类器, 即通过判定样本与不同类别聚类中心之间的距离远近做出分类, 比较适合数值变量处理.
(1)寻找边界样本, 更新其边界样本抽样概率.
传统的随机森林法采用随机抽取法构建分类集, 尽管具有泛涵性, 但由于边界样本占总样本比例较少, 这种分类集不能保证对边界样本的学习能力, 而边界样本判别的准确率决定着这个系统的预测精确度. 如何识别出边界样本? 本文思路如下: 从训练集突水样本(突水样本少, 信息重要)中任选一样本k(图1中的红色圆点), 给定距离半径Cr, 从训练集中选择出与k的距离小于Cr的所有样本集. 如果样本集中未包含不突水, 增大Cr, 直至样本集中至少存在1个不突水样本, (如图1, Cr1圆中包含了3个三角类), 找出边界样本k1(实心三角); 再以k1为圆心, 逐次增加距离半径Cr, 直至分类集中至少包含1个圆类(如图1中, Cr2圆中包含了2个圆类), 然后找出另一个边界样本k2(绿色圆点), 找到边界样本k1和k2后, 根据附近点距离边界点的距离更新其附近样本的抽样概率.
假设训练集样本抽样概率p(i)=rand(), p(i)∈(0, 1)
令p(k1)=1, p(k2)=1
针对训练集任一样本点i, 其抽样概率的更新方法如下:
计算出k1和k2的中点k3;
fori=1 to N do //N为训练集样本总数
tp=p(k1)*d(k2, k3)/d(i, k3) //d表示两点之间的距离
| ${{if}}\;\; tp > 0{{.5 \; {{and}} \;tp > p}}\left( {{i}} \right)\;{{ then }}\;p\left( {{i}} \right){{ = tp}}$ | (1) |
end for;
考虑到i可能与其他边界样本的距离更近, 因此这里的更新条件要考虑tp>p(i). 边界样本抽样概率提高后, 构建分类器时, 便于分类集中包含不同类别的样本.

|
图 1 边界样本的查找法 |
(2)构建基分类集SD.
基分类集是用来构建基分类器的, 而分类通常依靠边界样本, 因此基分类集应尽可能包含边界样本(或其附近样本)信息. 随着分类器的增多, 更多边界及其附近样本抽样概率在提高, 后续分类集包含边界样本的比例增多, 整个模型的预测准确率提高. 考虑到煤矿突水非均衡集特点, 每次样本成对出现, 即随机选择某个别界样本(或别界附近样本)以及与之距离最近的不同类样本, 以保证基分类集中不同类别的样本数目均衡. 假设基分类集样本编号用数组TempD(Cn)表示, Cn表示基分类集样本个数.
Step 1. 构建边界样本列表Tube(k1, k2);
Step 2. 任取样本点k, 按照图2所示方法寻求边界点k1和k2, 如果k1和k2不在Tube列表中, 加入列表, 按照公式(1)更新训练样本的抽样概率;
Step 3. TempD(1)=k1:TempD(2)=k2:n=2;
Step 4. 产生随机概率P, 产生随机样本k;
Step 5. 如果样本k的抽样概率p(k)大于随机概率P, 样本k被抽取, 加入基分类器TempD数组, 按照以上所述边界样本寻找法, 寻找另类样本中与k样本最近的边界样本k’加入TempD.
Step 6. 如果基分类集中样本数n大于等于Cn, 转Step 7, 否则转Step 4;
Step 7. 根据抽取样本的编号TempD, 从训练集读取样本数据, 构建基分类集SD().
(3)构建基分类器.
以上构建的基分类集中包含随机抽取的样本和边界样本, 利用这些样本如何构建基分类器呢? 本文的思路为首先采用有监督学习技术, 即根据基分类集样本标签对样本分类, 求出各类的初始聚类中心, 然后采用无监督学习法(不考虑样本分类标签, 只考虑影响因素, 以揭示影响因素与样本类别的内在联系), 即通过K-means聚类法对基分类集样本进行学习, 若干次迭代学习后, 最终获取聚类中心, 根据样本与聚类中心的距离作为基分类器判别分类的结果, 考虑到在实际应用中, 每个影响因素对煤矿是否突水的影响度并不相同, 为此本文借鉴随机森林构建决策树的思想, 在构建基分类器时, 除了考虑训练集数据行信息(随机产生分类集)外, 同时随机抽取Ck个列变量(各基分类器所包含的列变量不同), 构建基分类器, 以提高分类器的多样性.
输入: Numk: 基分类器编号, 按构建次序进行编号; Cn: 基分类集样本数量; SD(i, j): 基分类集样本数据, i=1, 2,…,Cn, j=1, 2,…,23 (22个影响因素外加一个突水标签); Ck: 基分类器样本数据的维度 (共22个影响因素), 2≤Ck≤22;
输出: W(Numk,i)=1/0: 基分类器列变量(影响因素), i=1, 2,…,22, 其中有Ck个W(Numk, i)=1; CenterP(Numk, i): 分类器突水类中心, i=1,2,…, 22; CenterN(Numk, i): 分类器不突水类中心,i=1,2,…,22;
Algorithm makeClassifier(Numk, Ck, Cn);
W(Numk, i)=0; // i=1,2,…,22;
产生Ck个互不相等的整数ak, 1≤ak≤22;
W(Numk, ak)=1, 随机抽取ak个影响因素;
假设SD(k, 23)=1/–1; //1表示突水, –1表示不突水;
//采用有监督学习求出“1”类和“–1”类的初始聚类中心
for i=1 to Cn do
Tempi=D(i, 23);
FL(Tempi)= FL(Tempi)+1; //统计各类样本数;
TempCenter(tempi, j)=TempCenter(tempi, j)+SD(i, j); // j=1, 2, …, 22;
End for
//求出初始聚类中心
InitCenterP(Numk, j)=TempTenter(1, j)/FL(1);
InitCenterN(Numk, j)=TempTenter(–1,j)/FL(–1), j=1,2,…,22;
//依据两个初始聚类中心, 采用Kmeans无监督学习求出基分类类中心CenterP(Numk, i)和CenterN (Numk,i).
Repeat
for i=1 to Cn do
//计算样本i与初始聚类中心InitCenterP和InitCenterN的距离dP和dN, 计算方法见公式(2).
If dP<dN then
nP=nP+1;
IcenterP(j)=IcenterP(j)+SD(i, j); //j=1,2,…,22
Else
nN=nN+1;
IcenterN(j)= IcenterN(j)+SD(i, j); //j=1, 2, …, 22
End for
CenterP(Numk, j)= IcenterP(j)/nP; //j=1, 2, …, 22
CenterN(Numk, j)= IcenterN(j)/nN; //j=1, 2, …, 22
Compute新旧居类中心的误差E;
Until E不再发生明显变化.
两个样本x1和x2之间的距离计算采用公式(2):
| $d(x_1,x_2) = \sqrt {\sum\limits_{i = 1}^{22} {W({{Numk,}}i) \times {{({x_{1i}} - {x_{2i}})}^2}} } $ | (2) |
尽管基分类器对训练样本集进行了学习, 融合了众多的训练样本数据信息, 对多数样本有较好的分类准确率. 但单个分类器的稳定性、可靠性不能保障, 为此需要构建一系列的基分类器对测试集进行预测以达到“集成功效”. 由于分类器来自不同的训练样本, 它们对同一测试集的预测结果不一. 因此对这些分类器的预测结果进行投票从而确定最终预测结果. 若超过半数的分类器的预测结果为突水(或不突水), 则最终预测结果为突水(或不突水). 假设采用2n+1个分类器对同一测试集进行预测, 每个基分类器的预测正确率都为P. 根据概率统计学公式, 最终预测结果的正确率PA为:
| $PA = \sum\limits_{k = n + 1}^{2n + 1} {C_{2n + 1}^k \times {P^k}} \times {(1 - P)^{2n + 1 - k}}$ | (3) |
例如, 当采用11个预测正确率均为0.7的基分类器对同一测试集进行投票预测时, 根据公式(3)得到最终预测结果的正确率为0.92. 可见相较于单个弱分类器的预测正确率, 多个分类器综合分析法的正确率有很大的提高, 这就是集成功效, 最终形成一个强分类器.
3.2.1 基分类器预测性能指标公式(3)中的P为传统的预测准确率, 即正确预测数(TA=TP+TN, TP为正确预测的不突水样本数, TN为正确预测的突水样本数)所占样本总数比例, 假如TP=TP+2, TN=TN–2, 尽管P未变, 但对煤矿企业的来说, 一次突水误判, 企业将遭受致命打击. 为此为了选择出良好的分类器, 必须修订分类器性能衡量指标.
ROC(Receiver Operating Characteristic)曲线常被用来评价一个二值分类器的优劣, ROC曲线的横坐标为误判率(False Positive Rate), 这里对应不突水误判率; 纵坐标为正判率(True Positive Rate), 这里对应突水正判率. ROC曲线用构图法揭示敏感性和特异性的相互关系, 曲线下面积越大, 判别准确性越高. 本例中的物理含义为输出较少的代价(不突水误判率较低), 就能对突水样本获取较高的判别率. 这里将曲线下面积近似计算为:
| $SAUC = (1 + PT - NF)/2$ | (4) |
式中,PT为突水样本的正判率, NF为不突水样本误判率. SAUC不仅可以衡量某基分类的预测性能, 也是系统(强分类器)的预测性能衡量指标, 显然SAUC越大, 分类器预测性能越好. 考虑到一次突水事故将造成巨大损失, 本文的算法思想为确保PT=1的前提下, 力求NF最小, 即以牺牲不突水样本的最小误判率为代价, 换取所有突水样本的正判率.
3.2.2 基分类器权重分析集成学习就是利用众多的分类器综合评判, 分类器性能不同, 对最终判决结果的贡献不同, 所占权重就不同. 考虑到即使SAUC相同的分类器, 其分类规则与样本的匹配度也不相同, 所谓匹配度是指分类器规则与样本分类结果贴近的程度, 所以本文依据分类器的匹配度计算分类器的权重. 权重较大的分类器的两分类中心的中间点(图1中的蓝色点)连线, 就可以把整体样本划分为不同的类, 如图1所示.
假设某分类器的分类中心突水类和不突水类分别为kp和kn, 针对某突水样本j, 分类器正判匹配度ψP(j)和误判匹配度ψN(j)计算公式如下:
| $\psi P(j) = 1 - \frac{{d(j,kp)}}{{d(j,kp) + d(j,kn)}}$ | (5) |
| $\psi N(j) = 1 - \frac{{d(j,kn)}}{{d(j,kp) + d(j,kn)}})$ | (6) |
针对所有训练集样本, 利用公式(5)和(6)分别计算所有正判样本的匹配度和所有误判样本的匹配度, 然后根据公式(7)计算分类器k对训练集的匹配度.
| $\psi PN(k) = \frac{{\sum\limits_{i \in \text{正判}} {\psi P(i) - \sum\limits_{{{i}} \in \text{误判}} {\psi {{N}}({{i}})} } }}{{\sum\limits_{i \in \text{正判}} {\psi P(i) + \sum\limits_{{{i}} \in \text{误判}} {\psi {{N}}({{i}})} } }}$ | (7) |
在集成学习的过程中, 尽可能选取SAUC和ψPN较高的分类器, 分类器数目选定后, 对其匹配度归一化处理后, 可求取该分类器的权重, 为后续测试集样本准确预测奠定基础.
3.2.3 基于改进型Boosting的集成学习集成学习目前应用较为广泛的算法有Bagging和Boosting, 采用Bagging算法, 各分集随机抽样, 基分类器可以并行生成. Bagging算法具有“集成功效”, 并不具备“学习能力”. Boosting算法根据每次训练集之中每个样本的分类是否正确, 以及上次的总体分类的准确率, 修正各样本的抽样概率, 依据修正后的新数据集生成新的分类器, 基分类器串行生成. 这种学习能力可以提高错分样本抽样概率, 无法保证新分类器对其他样本的准确率, 为此本文提出改进措施:
(1) 新分类集构建时, 除了考虑错分样本, 提高了边界样本抽样概率, 确保分类集中边界样本的比例.
(2) 在保证分类器多样性的同时, 后续选择性能良好(权重较大)的分类器参与投票, 丢弃误判率较高的分类器, 见Step 3.
(3) 在集成学习(投票)时, 考虑了各基分类器的权重, 使判别结果更为客观、科学.
改进后的学习步骤如下描述:
Step 1. 设置合适的参数Cn, 采用3.1节的算法构建分类集SD.
Step 2. 采用makeClassifier算法构建基分类器, 计算分类器的突水样本的正判率PT, 如PT=1,Numk=Numk+1, 计算分类器的权重ψW(Numk), 转Step 3; 否则转Step 1.
Step 3. 如果分类器个数Numk大于突水样本总数, 并且ψW(Numk)>(Max(ψW)+Min(ψW))/2, 存储新分类器, 转Step 4; 否则丢弃新分类器, 转Step 1. 即选择性能良好的分类器, 减小振幅, 以便于模型快速趋于稳定.
Step 4. 针对所有的训练样本数据, 利用这Numk个基分类器进行分类预测, 每个训练样本预测结果如公式(8)计算.
| $Spr(i) = \sum\limits_{k = 1}^{NumK} {\Pr (i,k)*\psi w(k)} $ | (8) |
Pr(i, k)为第k个分类器对样本i的预测值, 取值1(突水)/–1(不突水), 如Spr(i)>0, 最终预测结果为突水, 否则为不突水.
Step 5. 对于训练集中所有预测结果错分的样本, 计算其错分概率. 假如某样本k, 其样本标签为1(突水), Numk个基分类器中有N (N>=Numk–N) 个分类器投票它为–1(不突水), 那么其错分概率计算为N/Numk.
Step 6. 错分样本的抽样概率被提高后, 再次调用3.1节的makeClassifier算法构建新的基分类器, 转Step 1.
重复Step 1和Step 6, 直至所有的样本数据都能分类正确, 或者经过若干次迭代后所有训练样本的整体分类正确率不再明显变化时, 退出循环.
4 实验分析按照第2节中的影响因素分析, 本次实验共收集华北煤矿(主要来自河北省和河南省的部分煤矿), 工作面突水情况样本数据1551个, 其中突水样本97个, 未突水样本1454个. 随机选取2/3的样本为训练集, 全部样本为测试集.
4.1 分类集样本数Cn对模型SAUC的影响集成学习的本质主要依靠众多分类器对某样本的分类投票结果来进行分类, 那么针对特定的样本集, 每个分类集的样本数量Cn如何取值以及时需要多少个分类器, 才能使系统预测性能趋于稳定, 目前还没有固定的计算方式, 例如随机森林需要构建多少个决策树使得系统预测准确率稳定, 只能通过实验来确定. 因此本次实验分别取Cn为20, 40和60, 考虑22个影响因素, 通过训练集构建一系列基分类器, 分类器总数为200进行测试, 这里测试的是对总体样本, 而不仅限于测试集. 实验结果如图2所示.

|
图 2 分类集样本数Cn对模型SAUC性能影响 |
当Cn取值为20和40时, 每个基分类器训练样本较少, 随机性较强, 不具有代表性, 随着分类器个数增加, 尽管系统预测准确率振幅有所减少, 但几乎不能稳定, 可见Cn取值不能过小.
当Cn取值为60时, 每个基分类器训练样本较多, 取样样本空间分布的代表性较强, 随着分类器个数逐渐增多, 当分类器个数大于97后(见3.2.3节), 模型可以选择性能优良的分类器, 振幅减小, 达到170个时系统SAUC趋于稳定于0.99.
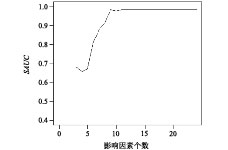
4.2 影响因素个数Ck对模型SAUC的影响为了构建更多的分类器及考察各指标因素对系统整体分类的影响, 在3.1节构建基分类器时, 并没有采用所有影响因素指标, 而是随机抽取Ck个指标, 就如同随机森林中的每个决策树的节点数, 节点数如何科学选取, 依然没有固定规律, 只能是针对特定的训练样本集通过实验分析获取. 为此本文针对不同的Ck =2,…, 22, 分别构建200个分类器进行测试, 实验结果如图3所示. 从图3不难发现, 当基分类器中的指标取12时, 系统SAUC稳定于0.99.
|
图 3 影响因素个数Ck对预测准确率的影响 |
4.3 集成学习能力对系统模型SAUC的影响
分类集样本数量Cn和煤矿突水影响因素Ck确定后, 系统的优化模型已经获取, 本节通过与Boosting算法比较, 分析本文算法的学习能力. 由于本文算法不仅考虑了错分样本抽样概率、并且充分考虑边界样本的分类影响、后续选择性能良好的分类器及通过加权综合考虑众多分类器的集成功效, 因此学习能力较强. 实验中参数Cn取60, Ck取12, 两种方法分别构建200个分类器进行测试, 实验结果如图4所示.

|
图 4 本文算法与Boosting算法模型SAUC对比 |
分析图4不难发现, 本文算法的集成学习功效表现在两个方面: 一是系统预测SAUC指标比Boosting高, 本文算法SAUC为0.99, Boosting算法学习能力差, SAUC稳定于0.96和0.97之间震荡; 二是系统预测性能SAUC稳定速度快, 尤其是在分类器数量大于突水样本数目之后, 本文算法在170个分类器时趋于稳定, Boosting算法在200个分类器时几乎不能稳定.
4.4 算法的预测准确度比较分析为了更全面的比较分析本文算法与其他模型性能, 随机抽取训练集(占总样本比例2/3)构建基分类器后, 以全体样本作为测试集, 共进行5次实验, 测试结果取平均值, 如表2所示.
| 表 2 工作面样本数据(1551:97)算法测试结果 |
由表2不难看出, 由于样本呈非均衡分布, 各种算法整体预测准确率PA取决于算法对不突水样本的预测率NT, 四种算法PA都在95%以上, 随机森林PA最高, 支持向量机和神经网络存在对不突水样本信息过分拟合, 泛函能力较差, 对突水样本预测率较低. 但观察PT和SAUC性能参数, 本文算法最好, 突水样本的正判率达到了100%. 在实际应用中, 误判的不突水样本其实危险系数很高, 已经接近于突水, 即使误判也是对煤矿企业突水安全工作敲响警钟, 督促企业提前预防、整改; 而突水的精准、无误差判别, 才是重中之重, 是煤矿突水预测的最根本目的.
5 结论煤矿突水预测关系着国民经济的重大发展及人民群众的生命安全, 是一个长期的系统工程, 同时基于大数据分析的预测技术已成为当前的研究热点. 本文在大数据分析技术的基础上, 考虑到样本数据集呈非均衡分布的特点, 提出一种基于集成分类的煤矿突水预测模型, 实验结果证明, 该算法可达到100%的突水样本正判率, 具有一定的现实意义, 且算法简单, 易于实现.
| [1] |
施龙青, 韩进, 宋扬, 等. 用突水概率指数法预测采场底板突水. 中国矿业大学学报, 1999, 28(5): 442-460. |
| [2] |
李博. 灰色关联——层次分析法的煤层顶板突水危险性评价模型. 河南理工大学学报(自然科学版), 2015, 34(3): 333-338. |
| [3] |
刘双跃, 陈丽娜, 王娟, 等. 基于模糊聚类分析和模糊模式识别的煤层底板突水区域预测. 矿业安全与环保, 2013, 40(2): 85-88. |
| [4] |
李建林, 张洪云, 王心义, 等. 脆弱性指数法在煤层底板突水预测中的应用与建议. 煤炭学报, 2014, 39(4): 725-730. |
| [5] |
刘再斌, 靳德武, 刘其声. 基于二项logistic回归模型与CART树的煤层底板突水预测. 煤田地质与勘探, 2009, 37(1): 56-61. |
| [6] |
王江荣, 赵睿, 文晖, 等. 基于Probit回归模型的煤矿底板突水预测. 中国煤炭地质, 2015, 27(3): 40-42, 48. |
| [7] |
许江涛, 邓寅生, 文广超, 等. 事故树分析法在矿井水害防治中的应用. 西安科技大学学报, 2009, 29(4): 405-409. |
| [8] |
雷西玲, 张景, 谢天保. 基于遗传神经网络的煤矿突水预测. 计算机工程, 2003, 29(11): 132-133. DOI:10.3321/j.issn:1002-8331.2003.11.044 |
| [9] |
姜成志, 张绍兵. 建立在神经网络基础上的煤矿突水预测模型. 黑龙江科技学院学报, 2006, 16(1): 8-11. |
| [10] |
陶一明, 刘瑞英. 基于BP神经网络的煤矿突水预测系统的设计. 内蒙古煤炭经济, 2012(12): 66-67. DOI:10.3969/j.issn.1008-0155.2012.12.042 |
| [11] |
胥良, 贾宪生. 基于神经网络的PID控制方法在矿井提升机中的应用. 工业仪表与自动化装置, 2015(2): 77-80. |
| [12] |
徐星, 孙光中, 王公忠. 基于层次分析法的矿井突水风险模糊综合评价. 工业安全与环保, 2016, 42(6): 26-29. |
| [13] |
刘仕瑞, 王凤英. 对兖矿集团Y煤矿突水的安全评价研究. 科技信息, 2013(10): 141. DOI:10.3969/j.issn.1673-1328.2013.10.135 |
| [14] |
魏军, 题正义. 灰色聚类评估在煤矿突水预测中的应用. 辽宁工程技术大学学报, 2016, 25(S): 44-46. |
 2018, Vol. 27
2018, Vol. 27


