计算机系统应用  2018, Vol. 27 Issue (4): 151-156   PDF    
引用本文
宋董飞, 徐华. 基于Spark的K-means改进算法的并行化实现. 计算机系统应用, 2018, 27(4): 151-156.http://www.c-s-a.org.cn/1003-3254/6296.html   
Song DF, Xu H. Parallel Implementation of Improved K-means Algorithm Based on Spark. Computer Systems and Applications, 2018, 27(4): 151-156(in Chinese).http://www.c-s-a.org.cn/1003-3254/6296.html   
基于Spark的K-means改进算法的并行化实现
宋董飞, 徐华     
江南大学 物联网工程学院, 无锡 214122
收稿日期：2017-07-23; 修改日期：2017-08-09; 采用时间：2017-08-14; csa 在线出版时间：2018-03-31
基金项目：江苏省自然科学基金(BK20140165); 国家留学基金委项目(201308320030)
摘要：针对传统K-means算法在处理海量数据时, 存在计算复杂度高和计算能力不足等问题, 提出了SKDk-means (Spark based kd-tree K-means)并行聚类算法. 该算法通过引入kd-tree改善初始中心点的选择,克服传统K-means算法因初始点的不确定性, 易陷入局部最优解的问题, 同时利用kd-tree的最近邻搜索减少K-means在迭代中的距离计算, 加快聚类速度, 并在Spark平台上实现了该算法的并行化, 使其适用于海量数据聚类,最后通过实验验证了算法具有良好的准确率和并行计算性能.
关键词: kd-tree    Spark    K-means    并行化    云计算    
Parallel Implementation of Improved K-means Algorithm Based on Spark
SONG Dong-Fei, XU Hua     
School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China
Abstract: In view of the problems that when processing massive data the traditional K-means is highly complex and insufficient in computation, a SKDk-means (Spark based kd-tree K-means) parallel clustering algorithm has been proposed. The algorithm improves the choice of initial center point by introducing kd-tree and overcomes the problem that the traditional K-means algorithm is easy to fall into the local optimal solution due to the uncertainty of the initial point. During K-means iterative calculation, the redundant computation has been reduced and clustering speed has been accelerated by the nearest neighbor search of kd-tree. The parallelization of the algorithm is realized on the spark platform and it is applied to the massive data clustering. Finally, the experimental results show that the algorithm has good accuracy and parallel computing performance.
Key words: kd-tree     Spark     K-means     parallel     cloud computing    

引言

随着移动互联网和物联网技术的不断发展, 极大地丰富和便捷了人们的生活, 但随之也伴随着巨量数据的产生. K-means作为典型的聚类算法, 已很难适应大数据环境下的数据处理要求, 其缺点主要表现为[1]: (1)随机选择初始中心点易使算法陷入局部最优; (2)迭代过程中需要进行大量冗余距离计算, 增加算法复杂度; (3)面对海量数据集, 传统的串行K-means算法运行效率低.

针对传统K-means算法的缺点, 已有很多学者在K-means的基础上提出了改进措施. 文献[2,3]引入通过引入canopy算法, 对K-means算法进行了优化, 利用canopy算法生成重叠子集, 在生成的重叠子集中进行聚类, 同时文献[2]提出了基于“最大最小原则”的canopy中心点选择方法, 解决了canopy选择的盲目性与随意性, 提高了算法的分类准确率, 但在实际应用中非常耗时. 文献[4]基于“距离最远的样本点不可能分到同一个簇中”这一事实, 提出了最大距离法选取初始簇中心的K-means聚类算法, 能够选取质量较好的初始中心点, 克服了传统K-means算法聚类结果不稳定和局部最优等问题. 文献[5,6]分别利用Mapreduce框架和Spark框架, 实现了改进K-means算法的并行化, 通过并行计算提高聚类速度, 使其适用于海量数据聚类中.

基于以上研究, 为了进一步减少数据聚类迭代过程中的冗余计算, 加快聚类速度, 提高聚类准确率, 本文提出了SKDk-means (Spark based kd-tree K-means)并行聚类算法. 文献[7]提出kd-tree数据结构, 将其应用在K-means迭代过程中, 加快聚类速度. 受文献[7]启发, 本文在初始点选取阶段引入kd-tree数据结构, 改善初始中心点预选取算法, 并在迭代过程中利用kd-tree解决了聚类过程中距离冗余计算的问题, 同时将改进后的算法部署在Spark平台上, 通过并行计算提高数据处理的速度. 本文实验分别以UCI标准数据集和人工产生的不同规模的数据集验证算法具有较好的聚类质量和并行计算性能, 更适合应用于海量数据的聚类分析中.

1 基于kd-tree改进的K-means聚类算法 1.1 kd-tree

kd-tree(k-dimensional tree)是由Bentley于1975年提出[8], k是空间数据对象的维度数, 在多维的空间数据结构中, kd-tree常用来数据索引和数据查询.

kd-tree的构建思想[9]是: 选择数据对象方差值最大的维度作为分割维度, 为了保证左右子树平衡, 在分割维度上选取数据的中值. 根据选取的维度和中值将k维数据空间划分为两个部分, 小于等于中值的点划分到左子树, 大于中值的点划分到右子树. 我们可以继续分别对这两个子k维空间进行如上划分, 又会得到新的子空间, 重复以上过程直到每个子空间都不能再划分.

kd-tree上的最近邻查找算法即在kd-tree中检索与某一查询点欧式距离最近的数据点[10]. kd-tree数最近邻查找算法思想如下: 从根节点递归地向下搜索, 进行二叉搜索; 搜索到叶子结点, 记为当前最近邻nearest; 进行回溯搜索, 如果超球面与父节点超平面相交, 进入相反的空间搜索, 更新nearest, 否则继续向上回溯, 回溯到根节点, 结束并返回最近邻.

1.2 基于kd-tree的初始中心点选取算法

给出一组n个对象 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n ) , 其中 x i = ( x i 1 , x i 2 , ⋅ ⋅ ⋅ , x i N ) . 在N维空间中选择数据对象方差最大的维度作为分割维度, 分割值为该维度上坐标的中值, 这样将数据集分割为左右两个大致相等的超矩形. 然后在每个超矩形上递归的执行分割, 直到任何超矩形不再划分为止.

该方法以方差最大维度上的坐标中值进行分割, 所以每个框中的对象个数大致相同. 该属性显示, 如果超矩形中的物体的密度比其他超矩形中的物体密度更高, 则该超矩形的体积更小.

假设超矩形i中所有对象的平均值为mi, 计算公式如下:

m i = ∑ i = 1 n x i n (1)

其中n表示超矩形中数据对象的个数, xi表示超矩形中的数据对象.

超矩形的密度, 顾名思义就是表示超矩形单元中数据对象的密集程度, 我们用ρi表示, 其定义如下:

ρ i = N i V i = N i ( max ( d max − d min ) ) 2 (2)

其中, Ni表示超矩形单元内数据对象数量; Vi表示超矩形的体积; dmax、dmin分别表示超矩形内数据的最大值和最小值.

q个超矩形的密度表示为 ( ρ 1 , ρ 2 , ⋅ ⋅ ⋅ , ρ q ) , 其对应的超矩形中心表示为 ( m 1 , m 2 , ⋅ ⋅ ⋅ , m q ) . 选择初始中心方法如下: 首先选择密度最高的超矩形中心mi作为第一个选取的初始中心点.

我们通过公式计算gi[11]来选择第2个初始中心点. 选择最大gi的超矩形中心mi作为第2个初始中心点

g i = d ( c 1 , m i ) * ρ i (3)

当第t个初始中心点已经被选择, 那通过下面的公式计算gi来选取第t+1个初始中心点. 选择满足gi最大超矩形的mi作为第t+1个初始中心点:

g i = { min k = 1 ⋯ t [ d ( c k , m i ) ] } * ρ i (4)

算法描述如下:

算法1. 基于kd-tree的初始中心点选取算法.

输入: 数据集 X = ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n ) , 聚类个数k.

输出: 初始聚类中心点 ( c 1 , c 2 , ⋅ ⋅ ⋅ , c k ) .

1) 创建给定数据集 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n ) 的kd-tree.

2) for j=1,…,q计算超矩形的中心mi和密度ρi.

3) 选择密度最大的超矩形中心作为第一个初始中心 c 1 = m z , 其中 z = arg max j ( ρ j ) .

4) for t=2,…,k:

for j=1,…,q计算 g i = { min k = 1 ⋯ t [ d ( c k , m j ) ] } * ρ j ;

第t个初始中心 c t = m z , 其中 z = arg max j ( ρ j ) .

5) 返回初始中心点 ( c 1 , c 2 , ⋯ , c k ) .

1.3 基于kd-tree的K-means算法

在kd-tree中采用最近邻查找思想, 检索kd-tree中与查询点距离最近的数据点, 可以很快速的找到最佳点, 而不需要进行过多的距离计算. 在K-means算法中, 我们引入kd-tree这一数据结构, 建立聚类中心点的kd-tree, 然后采用最近邻查找思想, 将各数据点分配给距离最近的中心点, 很好地解决了K-means算法聚类迭代过程中距离冗余计算的问题.

本文提出的基于kd-tree优化的K-means聚类算法的基本思想是: 首先应用基于kd-tree改进的初始中心点选取算法即算法1, 选取出k个有效的初始聚类中心点 C = { ( c 1 , c 2 , ⋯ , c k ) } . 然后建立聚类中心点集C的kd-tree, 数据点依次遍历kd-tree, 采用最近邻查找的思想, 将数据点分配给距离最近的中心点. 各数据点都分配给最近的聚类中心后, 进行全局的聚类中心点更新, 将更新后的聚类中心点与原中心点比较, 判断是否收敛. 若不收敛则进行迭代; 若收敛则退出迭代, 输出聚类结果.

算法描述如下:

算法2. 基于kd-tree优化的K-means聚类算法.

输入: 数据集 X = ( x 1 , x 2 , ⋯ , x n ) , 聚类个数k.

输出: k个最优聚类结果簇.

1) 应用算法1, 选出k个有效的初始聚类中心点 ( c 1 , c 2 , ⋯ , c k ) .

2) 建立中心点的kd-tree.

3) 将数据集中每个点依次遍历kd-tree:

① 从kd-tree根节点出发, 递归地向下搜索, 如果xi的当前维度上坐标值小于分裂点的值, 则进入其左子树进行搜索, 否则进入到右子树进行搜索, 直到叶节点为止, 记录下搜索路径, 将叶节点标记为Nearest, 计算叶节点与xi的距离Distance;

② 根据①中记录的搜索路径递归地向上回溯, 计算搜索路径上的每一个节点与目标点的距离, 如果其与目标点xi的距离小于Distance, 则更新此节点为最近点Nearest, 同时更新Distance, 比较Distance与xi到分裂轴的距离如果Distance比xi到分裂轴的距离大, 则需要向此节点父节点的另一个分支进行搜索; 否则继续回溯, 直到退回到根节点, 搜索结束, 此时的Nearest即为xi的最近聚类中心.

4) 更新聚类中心点, 并计算数据对象的误差平方和判断是否收敛, 若收敛则停止迭代; 否则进入2) 重复以上步骤, 直至算法收敛.

5) 输出k个最优聚类中心点, 完成聚类.

2 基于Spark的K-means算法并行化实现 2.1 Spark框架

Spark[12]由加州大学伯克利分校的AMP实验室开发, 在处理大规模数据时, Spark表现出其特有的优势. Spark通过引入内存计算, 在各计算节点内存内分布式缓存数据集, 从而大大减少了磁盘I/O操作时间, 这一特性使Spark特别适合运用于需要多次迭代的机器学习算法中.

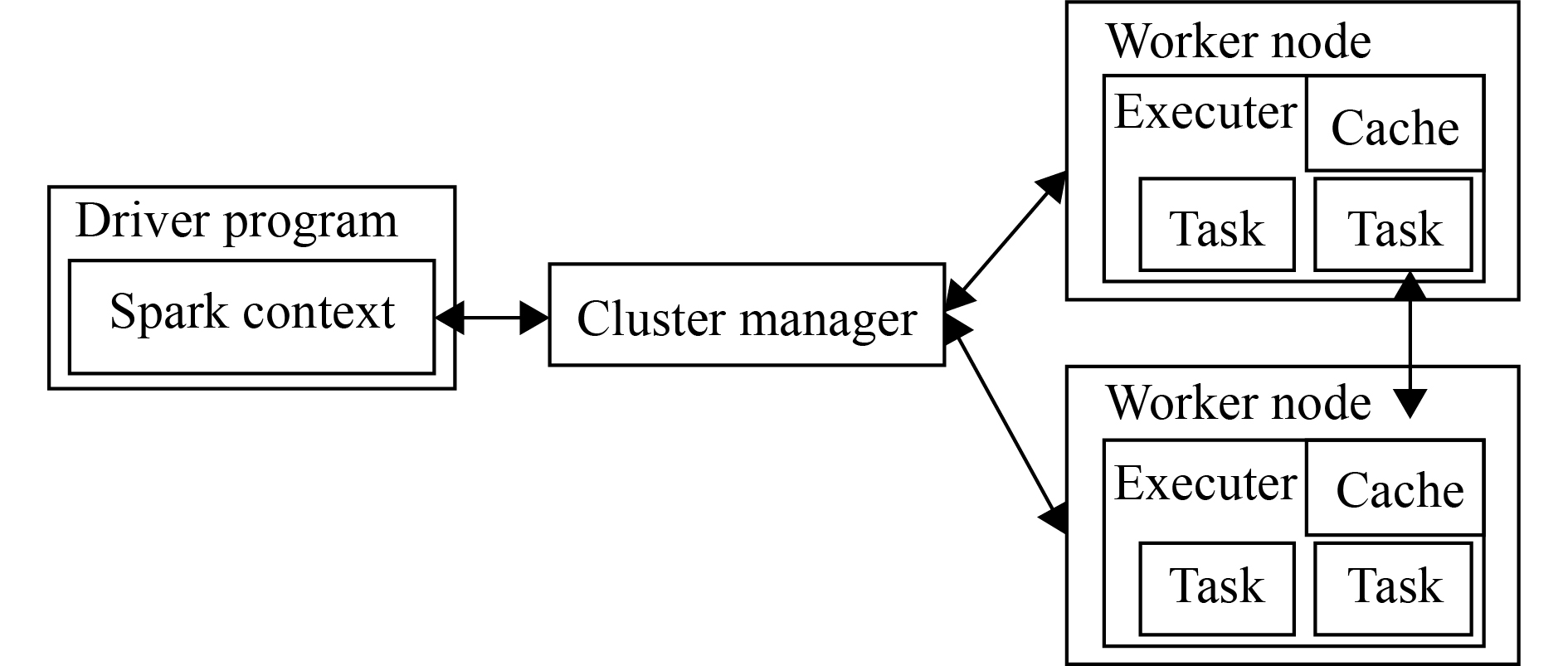
Spark运行架构如图1所示. Spark可以高效的部署在一个计算节点到数千个计算节点之间, 为了实现Spark集群在各个计算节点之间的通信与资源分配, Spark支持多种集群资源管理器(standalone、Mesos或Yarn). Spark context对象在主程序中负责总体调度, 并可与集群管理器相连接, 本文选择的是Yarn模式.

图 1 Spark运行架构图

2.2 初始点选取阶段

基于kd-tree改进的K-means算法改善了初始点选择问题, 并减少了迭代过程中的距离计算, 但kd-tree的建立以及kd-tree的搜索都需要花费很多的时间代价, 并不适用于海量数据的聚类. 本文利用Spark并行计算框架实现了基于kd-tree改进的K-means算法, 使其能应用于海量数据聚类中. 基于Spark的kd-tree优化K-means算法主要分为两个阶段: 初始点选取阶段和基于kd-tree的K-means并行阶段.

初始点选取阶段, 我们通过并行建树和并行计算各超矩形属性值, 在确保初始聚类中心点选择效果的同时, 减少初始点选择的时间. 启动算法, 集群从HDFS读取数据集形成初始RDD0; RDD0启动map算子执行Vectors.dense(), 将原始文本数据转化为可处理的向量数据键值对, 形成RDD1; RDD1启动map算子通过statistics.clostats计算数据方差最大的维度值, 并形成(维度值, 维度值上的数据值)形式的键值对, 保存为RDD2; RDD2启动reduceByKey、countByKey算子计算该维度上数据分割点split、该维度上数据个数count; RDD1启动map算子判断各条数据划分维度上的数据值与split的大小, 并据此进行左右子树划分, 左子树的键在原key后面添加0作为新的键, 右子树的键在原key后面添加1作为新键. 然后再依次对RDD1执行上述算子, 将左右子树进行划分, 每次循环的最后对相应RDD执行count函数, 计算出叶子节点个数, 当叶子节点个数大于聚类个数k时, 停止划分. 这样完成了kd-tree并行建树过程.

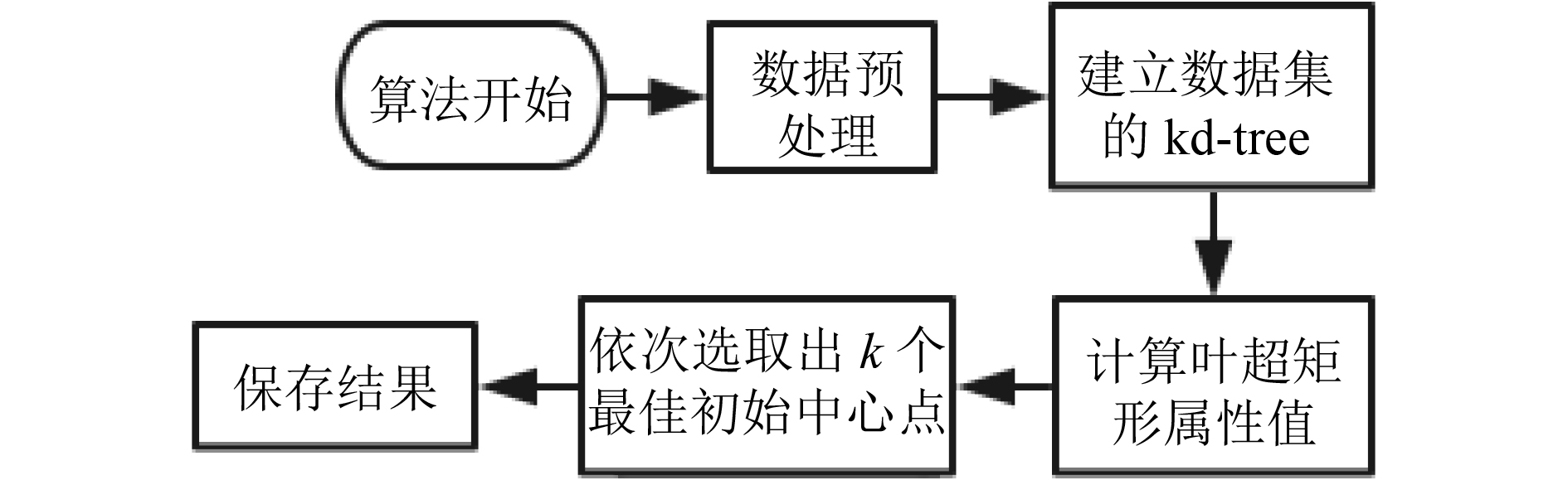
RDD1启动countByKey计算各超矩形中包含数据的个数, 记为countKey. 对RDD1启动reduceBy Key算子, 通过公式(1), 可计算出各个叶超矩形的中心点形成RDDm. 对RDD1启动reduceByKey算子, 通过公式(2)来计算出各超矩形的密度, 形成RDDd. 对RDDd启动reduceByKey计算出密度最大的超矩形, 并将其中心加入初始中心点集C中. 对于C中已有点, RDDm启动mapValues算子, 根据公式(4)计算出各超矩形的gi, 选出最大的gi的超矩形中心加入C中, 更新C继续迭代计算. 当C中点的个数为k时, 保存初始中心点数据, 程序结束. 初始中心点选取阶段流程如图2.

图 2 初始中心点选取流程图

2.3 基于kd-tree的K-means并行计算阶段

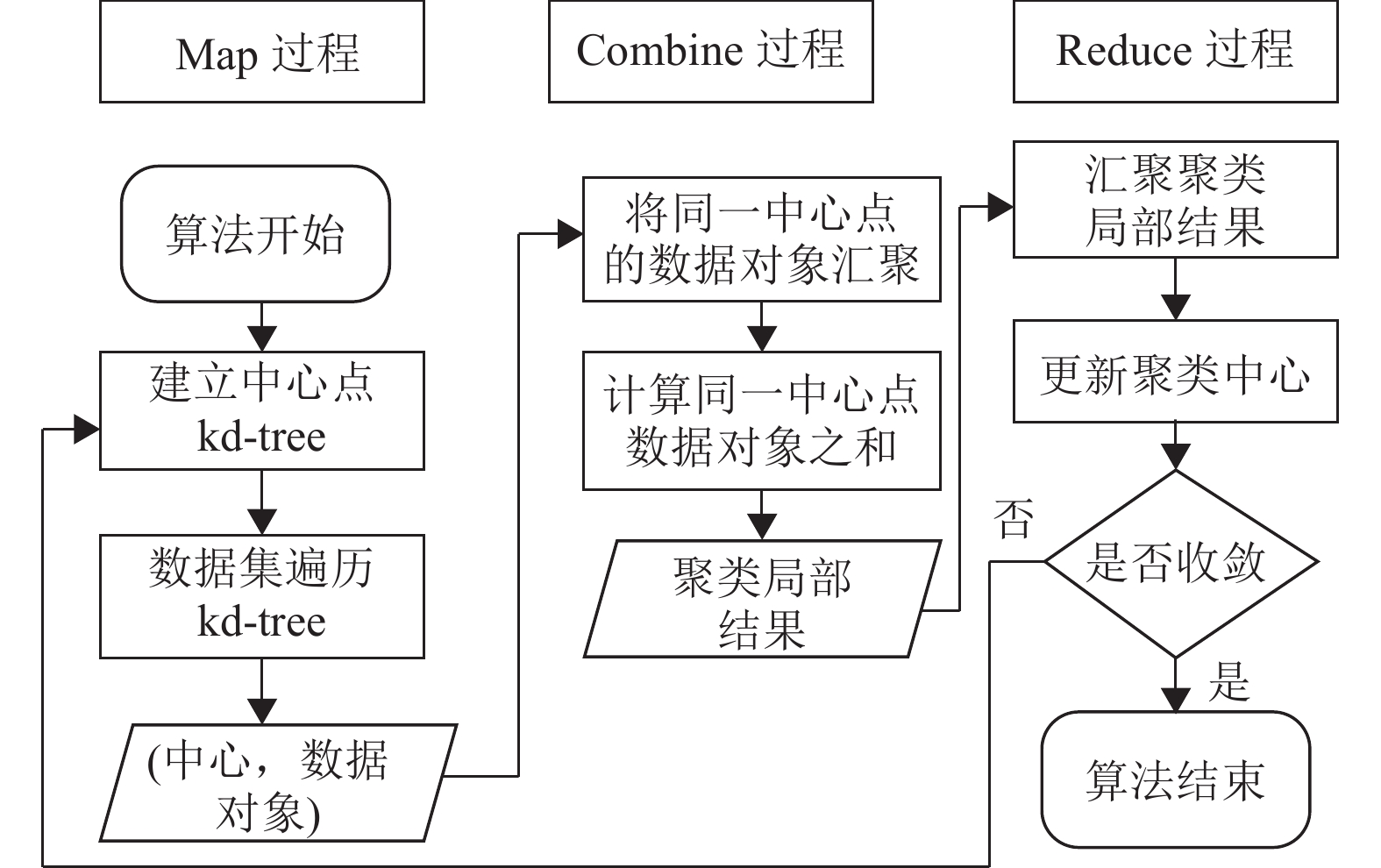
K-means算法利用kd-tree的最近邻搜索, 可以有效地减少迭代过程中不必要的距离计算, 将各个数据点快速划入所属簇中, 从而大大地加快了聚类速度. 各从节点间的并行计算, 总体上是采用“map”和“reduce”的思想, 并行计算流程图如图3所示.

图 3 SKDk-means并行聚类算法流程

算法开始, 程序读取初始中心点选取阶段选取的中心点数据, 建立初始中心点的kd-tree, 保存为center_tree, 并将center_tree作为广播变量发送给所有工作节点. 程序读取原始数据集保存为RDD_data, RDD_data启动map算子, map中的函数为kd-tree的最近邻查找函数: 首先比较数据点当前坐标是否小于分裂点的坐标, 如果小于进入左子树搜索, 否则进入右子树搜索, 直到叶节点为止, 标记为Nearest, 计算叶节点与数据点距离记为Nearest; 进行回溯搜索, 如果回溯点的超球面与父节点抄平面相交, 进入相反空间搜索, 更新Nearest, 否则继续向上回溯, 回溯到根节点, 返回Nearest. 数据集遍历kd-tree, 形成(Nearest, 数据点)形式的键值对, 记为RDD_kv. RDD_kv启动reduceByKey算子, 计算出新的聚类中心, 并计算误差平方和判断是否收敛, 若不收敛则建立新聚类中心的kd-tree, 进行迭代; 若收敛则输出聚类结果.

3 实验结果与分析 3.1 实验环境、实验数据及评价指标

实验采用阿里云平台的服务器, 创建了一个Master节点, 6个Slave节点. Master配置为8 G内存, 80 G硬盘; Slave配置为8 G内存, 160 G硬盘. Hadoop版本为2.7.2, Spark版本为2.0.2.

实验测试数据利用UCI[13]数据集下的Iris、Wine、Ecoli来验证算法的有效性, 数据集详细情况如表所示. 为了验证算法的并行效果, 采用了人工数据集Data1~4, 数据集详细信息如表1和表2所示.

表 1 实验测试数据集

表 2 人工数据集Data1~4

为了测试SKDk-means算法的整体性能, 采用以下评价指标: 准确率、加速比(Sizeup)、扩展比(Scaleup).

3.2 实验结果

1) 算法准确度

为了验证算法的有效性, 利用Iris、wine、Ecoli数据集进行20次实验, 取20次实验的平均值为最终值. 在传统k-means算法中, 由于每次聚类初始中心为随机选择, 聚类效果不稳定, 迭代次数较多, 而本文算法优化了初始中心点的选择, 拥有十分稳定的聚类结果. 由表3可知, 文本算法正确率高于传统k-means算法.

表 3 数据集测试结果

2) 算法扩展性

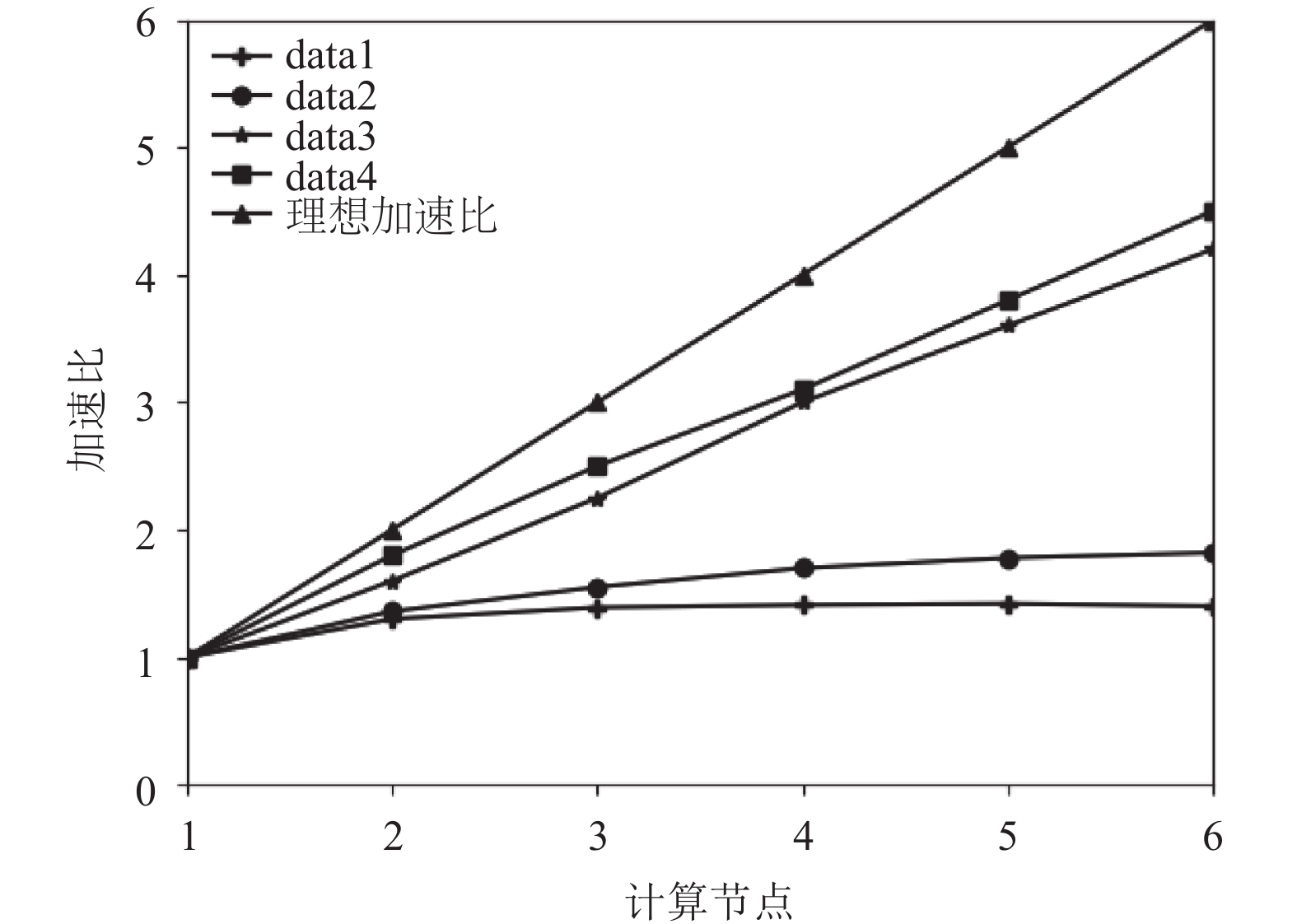
为了分析算法在Spark框架下并行执行的性能, 需要计算算法执行的加速比. 加速比是用来衡量程序执行并行化的重要指标. 算法的加速比曲线如图4所示. 在数据量较小时, 随着节点数的增加, 加速比开始时线性增加, 后渐渐趋于平缓或逐渐下降, 这是因为当数据规模较小时, 数据量远小于集群能够处理的数据量, 这时再将数据分成很多小块发送给各子节点, 随着子节点数目增加, 集群运行时间、任务调度时间、数据通信时间增加, 降低了计算速度, 此时并行效果不佳; 数据量较大时, 加速比随着节点数增加线性上升, 虽然距离“理想加速比”这个理想状态还很远, 但此时的并行效果已很明显. 这说明, 数据规模越大, SKDk-means算法的处理效率越高, 聚类效果越明显.

图 4 SKDk-means算法的加速比

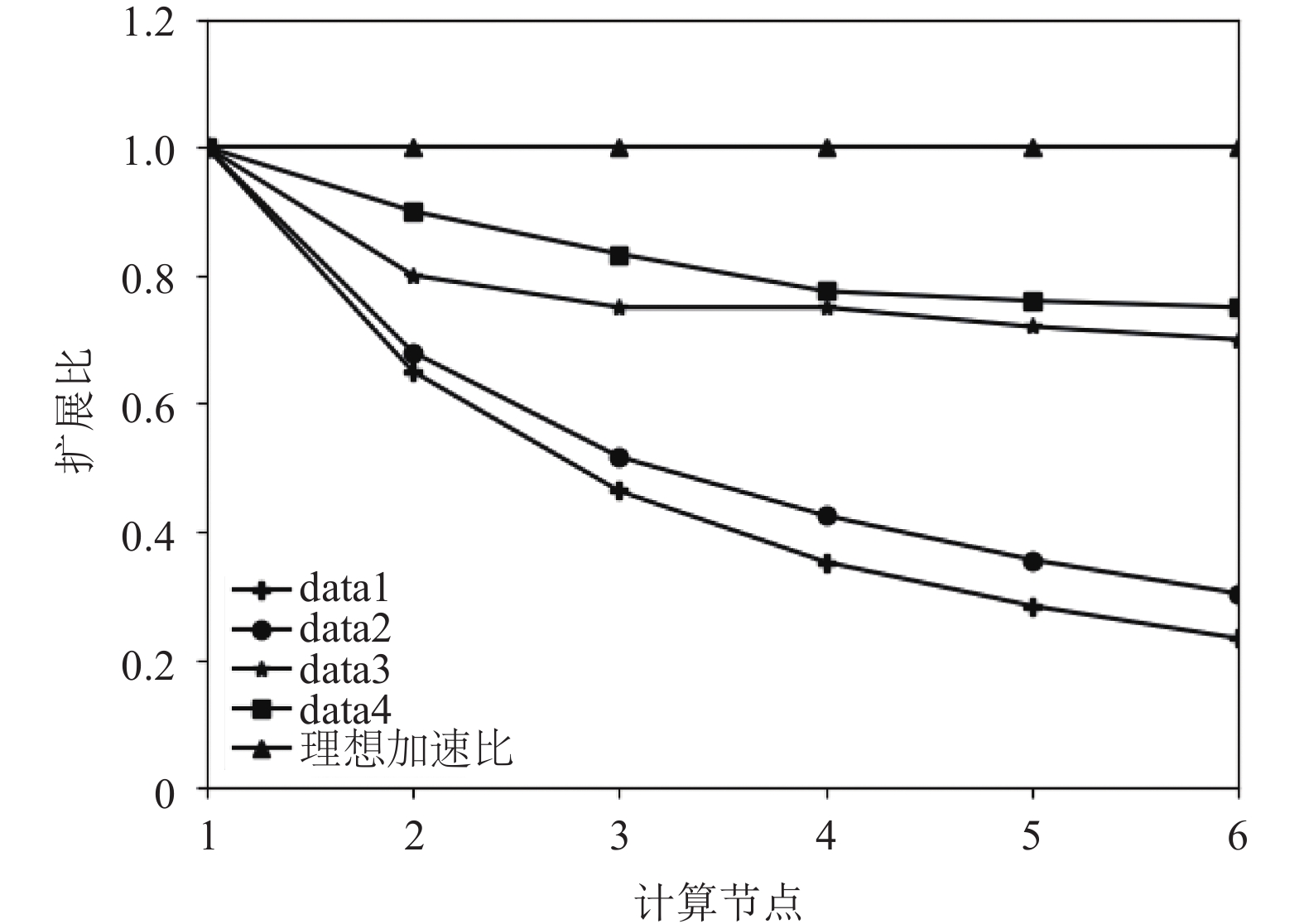
当集群中的计算节点的数目不断增加时, 并行算法的加速比并不能无限地增大, 此时仅用“加速比”已不能反映集群的利用率, 因此引入并行算法效率(扩展比)的概念. 如图5所示, 数据量较小时扩展比下降很快, 此时集群得不到很好的利用; 当数据量增大时, 扩展比下降速率相对趋缓, 并逐渐趋于稳定. 综合算法的加速比和扩展比, 样本规模越大, SKDk-means算法的处理效率越高, 聚类效果越明显.

图 5 SKDk-means算法的扩展比

4 结束语

本文针对传统K-means算法随机选择初始点及迭代过程中冗余距离计算问题, 通过引入kd-tree数据结构, 对算法进行了改进, 并将改进后的算法应用于Spark大数据计算框架, 实现了算法的并行化. 实验验证了该算法具有较高的聚类准确率, 并且具有优良的加速比和扩展比, 适合应用于海量数据聚类中.

参考文献
[1]
孙吉贵, 刘杰, 赵连宇. 聚类算法研究. 软件学报, 2008, 19(1): 48-61.
[2]
毛典辉. 基于MapReduce的Canopy-Kmeans改进算法. 计算机工程与应用, 2012, 48(27): 22-26, 68. DOI:10.3778/j.issn.1002-8331.2012.27.005
[3]
衣治安, 王月. 基于MapReduce的K_means并行算法及改进. 计算机系统应用, 2015, 24(6): 188-192.
[4]
翟东海, 鱼江, 高飞, 等. 最大距离法选取初始簇中心的K-means文本聚类算法的研究. 计算机应用研究, 2014, 31(3): 713-715, 719.
[5]
张石磊, 武装. 一种基于Hadoop云计算平台的聚类算法优化的研究. 计算机科学, 2012, 39(S2): 115-118.
[6]
刘鹏, 滕家雨, 张国鹏, 等. 基于Spark的大规模文本k-means并行聚类算法. 第二届CCF大数据学术会议论文集. 北京, 中国. 2014. 1–11.
[7]
Tiwari S, Solanki T. An optimized approach for k-means clustering. 9th International ICST Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness. 2013. 5–7.
[8]
Bentley JL. Multidimensional binary search trees used for associative searching. Communications of the ACM, 1975, 18(9): 509-517. DOI:10.1145/361002.361007
[9]
陈晓康, 刘竹松. 基于改进Kd-Tree构建算法的k近邻查询. 广东工业大学学报, 2014, 31(3): 119-123.
[10]
Panigrahy R. An improved algorithm finding nearest neighbor using Kd-trees. Proceedings of the 8th Latin American Conference on Theoretical informatics. Búzios, Brazil. 2008. 387–398.
[11]
Redmond SJ, Heneghan C. A method for initialising the K-means clustering algorithm using Kd-trees. Pattern Recognition Letters, 2007, 28(8): 965-973. DOI:10.1016/j.patrec.2007.01.001
[12]
Zaharia M, Chowdhury M, Franklin MJ, et al. Spark: Cluster computing with working sets. Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing. Boston, MA, USA. 2010. 10.
[13]
UCI. UCI machine learning repository. http://archive.ics.uci. edu/ml, 2015-03-30.