基于轨迹相似度的伴随人员推荐

引用本文

廖闻剑, 田小虎, 邱秀连. 基于轨迹相似度的伴随人员推荐. 计算机系统应用, 2018, 27(4): 157-161.http://www.c-s-a.org.cn/1003-3254/6295.html

Liao WJ, Tian XH, Qiu XL. Companion Recommendation Based on Trajectory Similarity. Computer Systems and Applications, 2018, 27(4): 157-161(in Chinese).http://www.c-s-a.org.cn/1003-3254/6295.html

基于轨迹相似度的伴随人员推荐

廖闻剑^1,2, 田小虎^1,2, 邱秀连¹

1. 南京烽火软件科技有限公司, 南京 210019;
2. 武汉邮电科学研究院, 武汉 430074

收稿日期：2017-07-24; 修改日期：2017-08-09; 采用时间：2017-08-14; csa 在线出版时间：2018-03-31

通讯作者：田小虎, E-mail: tianqianshmily@qq.com.

摘要：移动网络和智能终端的发展使得基于优质用户的伴随人员的推荐成为互联网发展的热点之一, 而伴随人员的推荐算法则是至关重要的因素. 针对以往基于地理位置的用户轨迹性相似推荐算法中需基于地理位置或基站数据, 且数据稀疏时推荐结果不理想的问题, 提出了基于IP场所的轨迹余弦相似度的伴随人员推荐, 以更完善的IP场所数据代替地理位置数据, 以一段时间的纵向日期和横向时刻分别计算余弦相似度以消除数据稀疏性问题. 最后推荐出了相似度质量更高的伴随人员.

关键词: 移动轨迹 IP场所推荐算法余弦相似度伴随人员

Companion Recommendation Based on Trajectory Similarity

LIAO Wen-Jian^1,2, TIAN Xiao-Hu^1,2, QIU Xiu-Lian¹

1. Nanjing FiberHome Software Technology Co. Ltd., Nanjing 210019, China;
2. Wuhan Research Institute of Posts and Telecommunications, Wuhan 430074, China

Abstract: With the development of mobile networks and intelligent terminals, the recommendation of the companion based on high-quality users has become one of the hot topics in the Internet, and the recommendation algorithm about companion is the crucial factor. In the past, the user location trajectory similarity recommendation algorithm was mainly based on geographic location or base station data and the data sparse may result in undesirable results. This paper proposes a companion recommendation model based on the cosine similarity of IP sites. More comprehensive IP sites data have been used instead of geographic data, and the date time data are calculated for cosine similarity to eliminate the data sparseness problem. Finally, the people with higher similarity and higher quality are recommended.

Key words: mobile trajectory IP sites recommendation algorithm cosine similarity companion

随着移动通信和互联网应用的快速发展, 移动用户对手机和互联网的依赖性和使用率越来越高, 移动运营商和互联网服务商积累了大量移动用户的实时IP数据. 分析移动用户的位置相似性、移动轨迹相似性, 发现同一用户使用的不同手机或者使用不同ID账号或者同行人员的情况, 以上都可以列入未被发现的潜在伴随人员, 潜在伴随人员的发现具有巨大的商业价值.

但目前关于用户轨迹相似性的研究主要是基于位置的社交网络(LBSN)用户轨迹相似性推荐^[1–3]或基于最长公共子序列(LCSS)的用户轨迹相似性推荐^[4,5]. 如陈少权^[6]结合TP数获得用户常驻区域解决用户轨迹随机性而改进的LCSS算法. 曹孟毅^[7]等利用Geohash编码快速搜索计算用户历史路线和推荐路线的相似度并不断调优的基于内容相似度的推荐算法. Chen^[8]等研究了基于位置的社交网络中用户通常访问时间和访问地点的规律性. Li^[9]等利用GPS日志计算用户活动轨迹的相似性. 由于LBSN是基于位置签到, 仅通过位置来分析用户的相似性过于片面. 而LCSS由于用户轨迹数据的稀疏性导致算法效率低下^[10]. 本文以某小区基站实时IP数据做支撑, 结合时间序列信息和IP位置, 并补充IP下出现的全部用户完整信息, 解决稀疏性问题, 建立以余弦相似度做相似性推荐的伴随人员推荐模型.

1 轨迹相似度的伴随人员推荐模型 1.1 基于IP轨迹相似度的推荐模型

移动用户的轨迹显示出高度的空间及时间规律性, 多数情况下个体会在较为固定的场所活动, 这是基于移动轨迹的研究的前提, 而之前的研究中的场所多指的是地理场所, 本文分析的场所是IP场所, 并不是固定不变的地理场所, 而是会变动的. 但是IP场所的研究更加符合互联网时代的伴随人员实际情况. 现阶段WLAN已经基本普及, 家庭、公司、餐馆等场所基本都已接入, 而WLAN在一段时间内的IP是固定不变的, 只要是接入WLAN的设备, 联网的IP都是一样的, 不同的只是端口, 只需要记录设备的联网IP和接入时间即可做伴随分析. 一段时间内每天纵向的登录次数和每个横向小时的登录次数都相似的话基本上是伴随人员.

本文提出的基于轨迹相似度的推荐模型, 从要分析伴随的原始人员出发, 完整记录N天内的登录轨迹(ID+IP+TIME), 并完整记录出现过的IP的这段时间内的全部记录, 以纵向天数登录建立N维向量, 再以横向的每天24小时, 建立24维向量, 最后加上登录的IP(即IP场所)都以余弦相似度做相似度的衡量算法, 以原始人员作为训练集, 以IP内出现的其他人员作为测试集, 最后推荐出相似轨迹行为的伴随人员.

1.2 轨迹相似度算法的选择

相似度衡量的方法有很多, 常见的有欧式距离、编辑距离(Edit Distance on Real Sequence, EDR)^[11]、最长公共子序列(Longest Common Subsequence)^[12]、动态时间调整(Dynamic Time Warping, DTW)、最大时间出现法(Maximum Co-occurrence Time, MCT)、余弦相似度等, 这些算法分别适应的不同的数据类型和应用场景^[13–15]. 基于本文的轨迹数据情况, 以下重点介绍基于加权欧式距离的移动轨迹相似度、基于编辑距离的Lenvenshtein算法以及本文选用的余弦相似度算法.

(1) 加权欧式距离

欧式距离是计算每个时间点上轨迹对应的两个点的欧式距离, 加权欧式距离是将轨迹点在时间维度上划分, 每个时间段内的特征点进行特征提取, 并给不同的时间段赋予不同的权值, 例如, 筛选家庭成员则给予夜间时间区间以较高的权值, 筛选学习工作同伴则给予日间时间区间以较高的权值.

(2) Lenvenshtein算法

编辑距离是指由原向量P转换到目标向量Q所需的最少编辑次数. 这里编辑操作的含义是: 对向量指定位置的单个元素进行插入、删除、替换的操作.

(3) 余弦相似度

以上两种常应用在轨迹相似度中的衡量算法, 加权欧式距离在考虑时间维度及保留数据特征情况下, 降低了数据比较过程中的数据量, 但很多时候登录轨迹是从宏观一段时间内的伴随, 对相对时间内的登录场所并不敏感; 而编辑距离需要对每个指定位置的每个元素持续比较并作出相应的增删改查等操作, 数据处理的时间复杂度较高, 且在数据稀疏时效果不理想.

综合以上考虑, 为了同时应付数据稀疏情况和相对时间内数据不敏感的情况, 本文选择余弦相似度算法作为相似性度量, 同时考量了相对时间段内的伴随及宏观时间内的伴随, 降低某段时间内数据稀疏导致结果不理想的问题, 且不必针对每个指定位置元素单独分析相似度, 而是一起做相似性度量, 降低了时间复杂度.

而要计算两个向量X(x₁, x₂, …, x_n)和Y(y₁, y₂, …, y_n)之间的相似度除了欧氏距离, 还有明可夫斯基距离:

d i s t (X, Y) = {(\sum_{i = 1}^{n} {| x_{i} - y_{i} |}^{p})}^{1 / p}

(1)

其中, p=1时是曼哈顿距离, p=2时是欧氏距离, p无穷大时是切比雪夫距离, 这些距离在处理轨迹数据时, 有一个共同点, 就是绝对数值敏感, 将其中一个向量的维度扩大或缩小n倍, 距离改变.

另一个系列是通过计算向量之间的夹角来表示距离, 该系列主要有余弦相似度、调整余弦相似度和皮尔森相关系数, 这个系列的算法最大的特点就是对绝对数值不敏感, 只对向量的方向敏感, 就是说把向量的维度扩大或缩小n倍, 距离值不变. 目前用的最多的就是余弦相似度, 调整余弦相似度是特殊情况下对余弦相似度的调整, 皮尔森相关系数是数据中心化后的余弦相似度, 多用于线性回归.

本文的研究是为了找出伴随人员具体是两个用户的登录轨迹是否相似, 对用户的维度(登录次数)不敏感, 因此选择余弦相似度, 公式如下:

d i s t (X, Y) = \cos θ = \frac{\vec{x} \cdot \vec{y}}{| | x | | \cdot | | y | |} = \frac{\sum_{i = 1}^{n} x_{i} y_{i}}{\sqrt{\sum_{i = 1}^{n} x_{i}^{2}} \cdot \sqrt{\sum_{i = 1}^{n} y_{i}^{2}}}

(2)

现根据余弦相似度算法提出轨迹相似的伴随人员推荐模型如图1所示.

图 1 基于余弦轨迹相似度的伴随人员推荐模型

1.3 算法相似度阈值的确定

利用公式2判定图1中的相似度时, 需要分别从纵向的日期和横向的时刻判定余弦相似度. 而且在实际的应用情景中还会遇到公共IP场所的情况, 公共IP场所下登录的用户ID众多, 且大部分是不想关的人员, 因此比较的意义不大而且会徒增算法复杂度, 因此有必要排除公共IP场所的影响.

以上余弦相似度和公共IP场所的判定都需要设定判定的阈值, 以确定相似与否及是否为公共IP场所, 阈值的设定需满足误判率低和切合实际, 误判率低是尽量不造成原始样本的少取带来的误差. 而实际指的是同一IP出现的ID数量不大, 但当出现的ID次数较大时的IP又较少, 综合历史实际情况出现ID较少的IP和出现ID较多的IP(公共IP)分布判定比例为7:3, 这是因为实际情况下公共IP出现的ID一般都较多. 且本文根据设定的原始阈值不断对确定的样本进行训练, 进一步优化了阈值.

2 实验测试 2.1 实验数据源

数据源来自于烽火通信公司及职工小区2017-03-09到2017-06-06这90天的上网登录记录, 该数据是通过Wifi设备采集并记录得来的, 数据至少包含用户唯一ID、IP、时间等信息. 记录场所广阔, 人员驳杂, 大部分人员并不相识, 住所也不尽相同, 同时还有外来人员的访问等, 因此适合做伴随人员的分析.

2.2 实验过程

本实验以日期分布、时刻分布、IP分别三个切入视角进行维度提取和相似度计算.

Step 1. 针对随机抽取的5个原始用户, 获取这5个用户ID在90天内完整的登录记录(ID+IP+ TIME), 共得到896条记录, 其中IP去重后为434条.

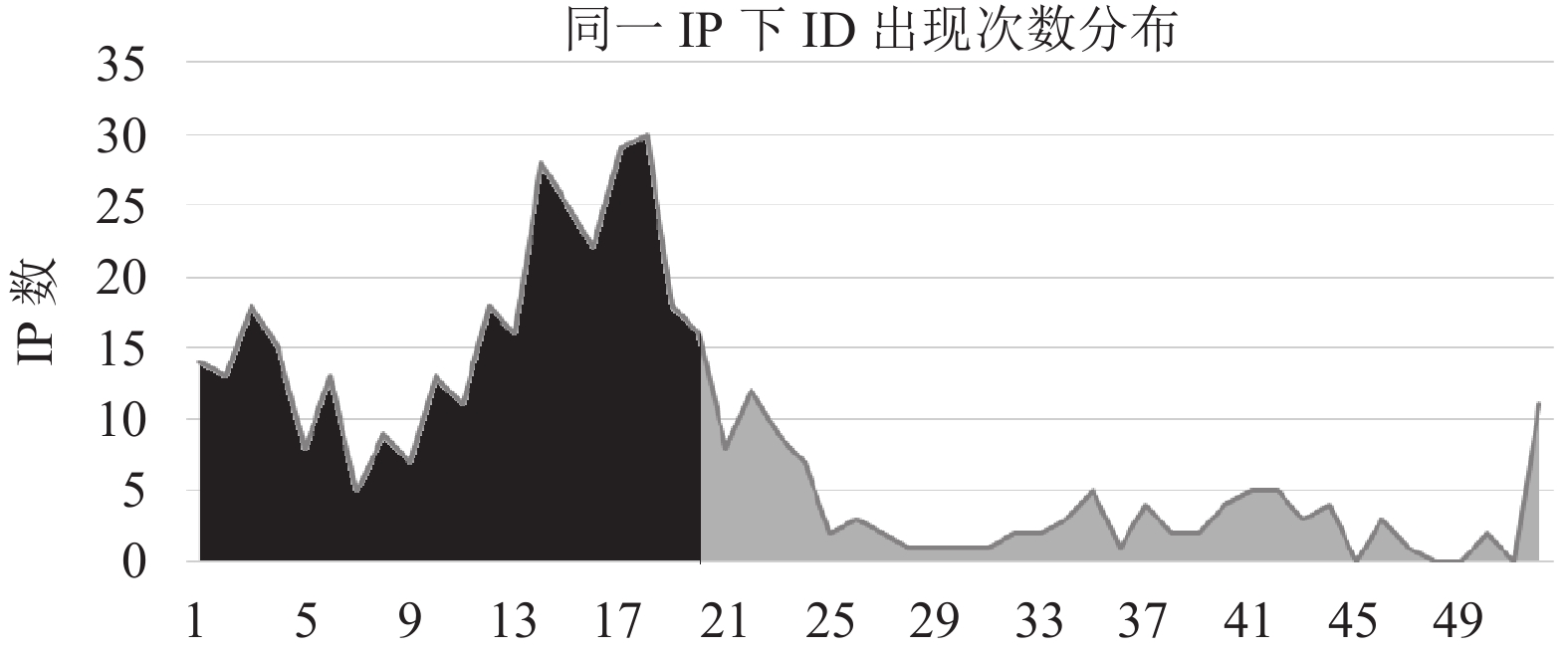
Step 2. 获取448个IP下所有的出现过的ID信息, 共得到76 180条记录, 这些IP中有公共IP的存在需要过滤掉. 过滤公共IP主要是看IP下出现的ID数, 超过一定ID次数阈值的IP很可能是公共IP, 如图2所示, 绝大部分IP下出现的用户ID数都小于20, 20之后IP数量明显减少, 考虑到作为模型的首次过滤, 过滤比例不能太大, 以免过滤掉有效数据, 再结合样本的实际情况将IP下用户ID出现次数阈值定为20, 最后得到非公共场所的有效IP为312个, 得到有效登录用户ID为1470个.

图 2 同一IP下ID出现次数分布情况

Step 3. 按照日期分布分析, 把5个原始用户在2017-03-09到2017-06-06这90天间每天的登录次数构成一个90维的向量(x₁, x₂, …, x₉₀)代表第i天的登录次数, 我们把1470个样本用户的登录向量分别和5个原始用户的登录向量按照公式(2)算夹角余弦, 因为都是整数, 所以余弦值范围在0–1之间, 如果值越接近1, 代表这两个向量越相似, 也就说明这两个账号的轨迹日期分布越相似, 根据阈值确定的的原则, 确定阀值为0.75, 就是说如果两个向量余弦值大于等于0.75, 我们认为他们的轨迹日期分布相似.

Step 4. 按照时刻点分布分析, 把5个原始用户在00到23点的登录次数构成一个24维的向量(y₁, y₂, …, y₂₄)代表第j时刻的登录次数, 我们把1470个样本用户的登录向量分别和5个原始用户的登录向量按照公式(2)算夹角余弦. 不过由于时刻分布只有24个维度, 而日期分布有90个维度, 所以确定时刻分布相似的阀值需要比日期分布阀值高, 按照阈值确定原则, 确定阈值为0.9, 即余弦值大于0.9, 我们就认为这两个账号的轨迹时刻分布相似.

Step 5. 按照登录IP分析, 5个原始用户在90天内的所有登录IP, 如果在样本用户的IP中有半数以上相同, 则认为两个用户的轨迹IP相似.

2.3 实验结果

将原始5个抽样人员依次编号为1~5, 根据公式10分别计算的日期、时刻和IP相似度分别计算和1470个其他用户的相似度, 不同维度的相似性, 其中择选相似度最高部分如表1所示.

表 1 相似度最高的部分人员

ID	日期分布相似	时刻分布相似	IP分布相似	相似维度数
5985**	-	2, 5	2	2
18**85	2	5	-	2
41**92	2	5	-	2
43**97	2	5	-	2
5541**	2	2, 5	-	2
73**78	2	3, 5	-	2
76**74	2	3	-	2
76**56	2	5	-	2
84**65	2	5	-	2
91**04	2	3	-	2
91**40	2	3	-	2
10**52	2	3	-	2
12**19	2	3	-	2
14**04	2	3	-	2
14**81	2	5	-	2
15**97	2	5	-	2
16**75	2	3, 5	-	2
19**17	2	3, 5	-	2
21**26	2	5	-	2
2262**	2	2, 5	-	2
24**62	2	3	-	2
25**95	2	3	-	2
2762**	2	2	-	2
31**38	2	5	-	2
33**91	2	5	-	2
35**12	2	5	-	2
35**89	2	5	-	2
2490**	-	-	4	1
3373**	-	-	3	1

表 1 相似度最高的部分人员

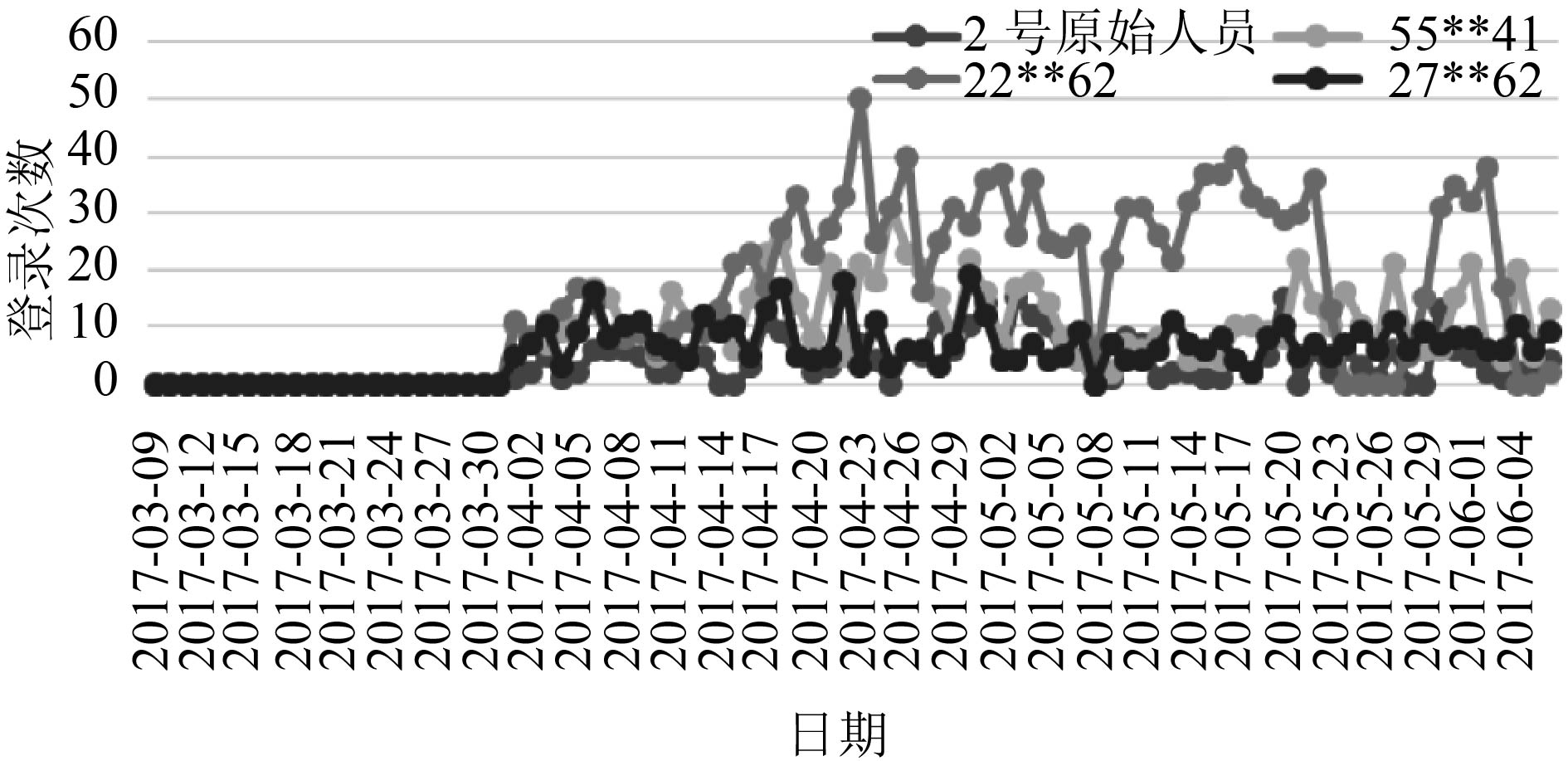
可以看出表1中标粗的6个ID跟原始抽样人样人员轨迹极为相似, 详见图3和图4. 再补充加入IP相似, 详见表2. 如果一个ID一段时间内登录的IP中有超过一半另一个账号都登陆过, 再加上之前两个相似性特征, 那就足以说明伴随了. 综合以上3个维度, 59**85, 55**41、22**62、27**62、33**73、24**90这几个新得到的人员为伴随人员.

图 3 横向时刻登录次数分布对比

图 4 纵向日期登录次数分布对比

表 2 相似人员相同IP登录情况

最后根据对公司人员的调研数据和外来人员的登记数据, 最终确认59**85, 55**41、22**62、27**62为2号抽样人员的伴随人员, 24**90为4号抽样人员的伴随人员. 判断准确率为83.3%.

3 结束语

本文使用IP场所的用户登录数据, 提出基于轨迹相似度的伴随人员推荐模型, 根据要分析的原始人员, 提取该人员在IP场所下的登录信息, 进一步提取IP下的相关人员, 利用余弦相似度算法计算原始用户和提取用户之间的轨迹相似度, 综合多维度推荐出最终的伴随人员. WLAN的普及使得IP数据的获取比以往基于地理位置的数据(基站数据、GPS数据等)更易获取, 且数据比经纬度数据容易处理. 以上结果表明: 1)基于IP场所的轨迹伴随比基于地理位置的伴随更加容易分析也更加实用; 2)本实验综合一段时间的纵向日期分析和横向时刻分析, 相对以往的降低了Lenvenshtein算法的维度和算法复杂度, 同时也降低了加权欧式距离中单位时间内数据稀疏性带来的误差.

参考文献

[1]	张莹, 李智, 张省. 基于位置的社交网络用户轨迹相似性算法. 四川大学学报(工程科学版), 2013, 45(S2): 140-144.
[2]	符饶. 基于位置服务的潜在好友推荐方法. 软件, 2015, 36(1): 62-66. DOI:10.11907/rjdk.143816
[3]	郭岩, 罗珞珈, 汪洋, 等. 一种基于DTW改进的轨迹相似度算法. 国外电子测量技术, 2016, 35(9): 66-71.
[4]	裴剑, 彭敦陆. 一种基于LCSS的相似车辆轨迹查找方法. 小型微型计算机系统, 2016, 37(6): 1197-1202.
[5]	肖啸骐. 一个有效的稀疏轨迹数据相似性度量. 微型电脑应用, 2014, 30(4): 25-30.
[6]	陈少权. 基于改进LCSS的移动用户轨迹相似性查询算法研究. 移动通信, 2017, 41(6): 77-82.
[7]	曹孟毅, 黄穗, 王会进, 等. 基于内容相似度的运动路线推荐. 计算机工程与应用, 2016, 52(9): 33-38, 55.
[8]	Chen L, Özsu MT, Oria V. Robust and fast similarity search for moving object trajectories. Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data. Baltimore, ML, USA. 2005. 491–502.
[9]	Hung CC, Chang CW, Peng WC. Mining trajectory profiles for discovering user communities. Proceedings of the 2009 International Workshop on Location Based Social Networks. 2009. 1–8.
[10]	赵作鹏, 尹志民, 王潜平, 等. 一种改进的编辑距离算法及其在数据处理中的应用. 计算机应用, 2009, 29(2): 424-426.
[11]	姜华, 韩安琪, 王美佳, 等. 基于改进编辑距离的字符串相似度求解算法. 计算机工程, 2014, 40(1): 222-227.
[12]	Lee SL, Chun SJ, Kim DH, et al. Similarity search for multidimensional data sequences. Proceedings of the 16th International Conference on Data Engineering. San Diego, CA, USA. 2000. 509–608.
[13]	Marascu A, Khan SA, Palpanas T. Scalable similarity matching in streaming time series. Proceedings of the 16th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin, Heidelberg, Germany. 2012. 218–230.
[14]	Vlachos M, Gunopulos D, Kollios G. Discovering similar multidimensional trajectories. Proceedings of the 18th International Conference on Data Engineering. Washington, DC, USA. 2002. 673.
[15]	Zheng Y, Zhou XF. Computing with Spatial Trajectories. New York: Springer, 2011.