2. 南京烽火软件科技有限公司, 南京 210019
2. Nanjing Fiberhome Software and Science and Technology Co. Ltd., Nanjing 210019, China
信息可视化通过将数据映射为容易感知的图形、符号、颜色等, 可以增强数据呈现效果, 让用户以直观交互的方式实现对数据的观察和浏览, 从而发现数据中隐藏的特征、关系和模式[1], 为其对数据做进一步分析和处理提供参考思路.
Web相关的人物关系可视化成果, 目前已有的百度知心、搜狗知立方等人物关系图, 都是近似于静态的展示, 交互性弱, 拓展和布局均是有限且固定的, 不能动态满足用户需求. 且未能对特定人物关系做出标识, 故本文研究无向图多最小环算法, 以便于隐含团体关系的求解.
类库D3.js是实现可视化的很好选择. 赵聪[2]和权庆乐[3]对D3的特性做了阐述, 权鑫[4]基于D3实现了可视化系统框架, Daniel等[5,6]将数据驱动应用于可视化取得了较好的效果, 但以上均未涉及人物关系的可视化实现.
Dijkstra算法是图论中求取最短路径的经典算法. 王树西[7]改进Dijkstra以求多条最短路径; 汤志贵[8]则讨论了基于Dijkstra求解最小环的朴素算法. 但并不能解决无向图多最小环问题.
本文结合D3.js可视化库的数据驱动、高效灵活的特点, 实现了以力导向布局为基础的人物关系图, 并结合需求, 改进了最短路径算法, 以求解无向图的全部最小环, 动态标识人物团体关系.
1 无向图经指定顶点的最小环算法对于由顶点集V和边集E构成的图
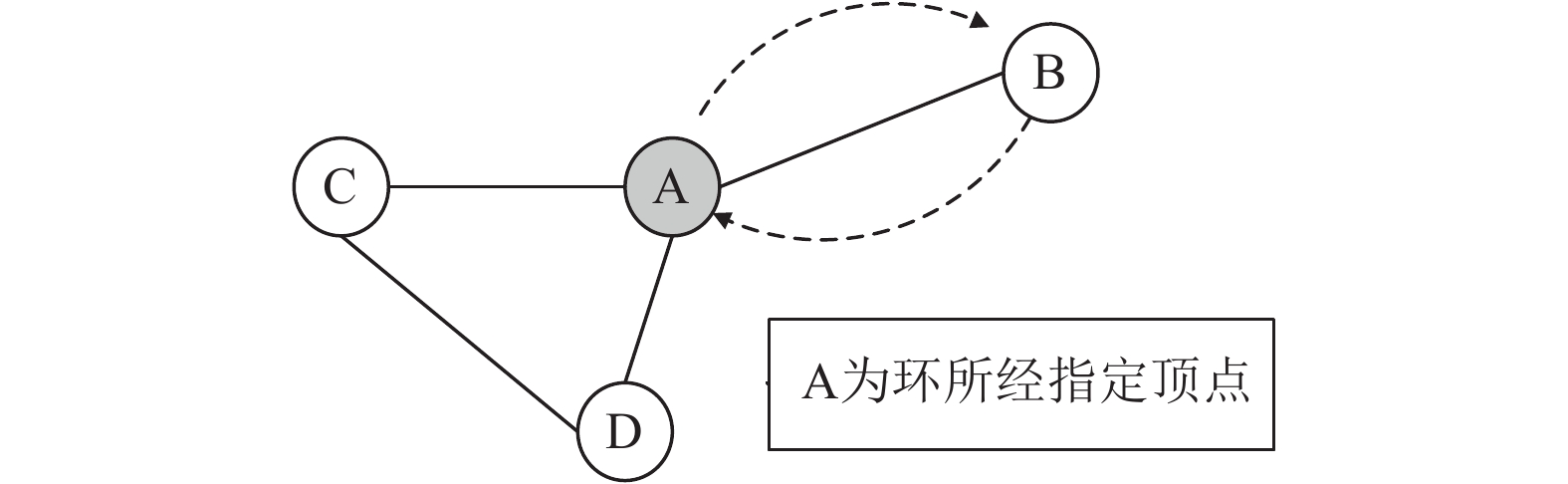
|
图 1 无向图邻接点自成“环” |
另外, 图中某顶点可能有多个邻接点, 故可能存在多条权重相同的最短路径. 由于Dijkstra在比较路径的“长短”时, 忽略掉等权重的路径, 仅当存在“更短”路径时, 才考虑更新最短路径. 致使结果只有一条最短路径, 用于求最小环, 也只能得一环.
对于上述弊端, 本文讨论与改进如下:
无向图G中顶点v的度记为
设预处理后的图为
求解无向图经指定顶点全部最小环算法伪代码实现如下:
G过滤满足
初始化matrix[][],pre_path[], dist[]
for u in
tmp = matrix[v0][u];
matrix[v0][u] = matrix[u][v0] = INF;//断开连接
for vi in N(G'):
for vj in N(G') ordered by dist:
if dist[vi]+matrix[vi][vj]<dist[vj]:
dist[vj] = dist[vi] + matrix[vi][vj];//更新最短距离
clear path[vj];
path[vj] = vi;//重置前置路径
elif dist[vi] + matrix[vi][vj] = dist[vj]:
path[vj].push(vi);//添加前置路径
End if
End for
End for
findPath(v0, u, path); //逆向跟踪路径, 得环集
matrix[v0][u] = matrix[u][v0] = tmp //恢复连接
End for
findShotestPath(v0, u);//全部环集中择最小环集
该最小环算法用于求解关系图的人物团体关系, 复杂度为
相较于文献[7], 本文算法考虑了多最短路径到多最小环的应用; 文献[8]虽讨论了最小环的求解, 但给出的两种算法均未考虑多邻接点问题, 且复杂度均为
数据驱动文档(Data Driven Documents)[11]是一个大数据下的开源可视化工具, 简称D3, 是基于数据的文档操作JavaScript库. D3 结合功能强大的可视化组件和数据驱动的方法对文档对象模型(DOM)进行操作, 可以将任意数据绑定到DOM. 将数据和HTML、SVG[12]、CSS结合起来, 创造数据图表. D3.js采用的是链式语法[13], 为开发者提供了便捷的调用方式. D3最突出的特性是数据驱动, 不隐藏用户原始数据, 避免了局限的数据展现, 提供了强大的灵活性.
本文的人物关系的可视化采用力导向布局, 该布局是模拟弹簧电荷模型, 在每两个节点间添加斥力, 每条边的两节点间添加引力, 每次迭代节点会在各个斥力和引力的作用下发生位移, 多次迭代后, 节点会静止于受力平衡的位置, 达到模型的能量最小化.
D3提供了诸多类型的布局(layout)函数, d3. layout.force就是D3中实现力导向布局的对象, 该对象封装了很多参数设定的方法. 其中, size方法用于设定画布尺寸和重心位置, linkStrength、linkDistance分别设置边强度和边长度, 摩擦系数friction主要影响速度衰减, 电荷作用力charge表现为节点间的引力或斥力, chargeDistance为引力作用距离, 向心力gravity以微弱牵引作用将节点吸引至布局几何中心. 力导向布局的结果有良好的对称性和局部聚合性, 在平面上布局产生很少的边交叉, 清晰美观.
2.2 d3.layout.force改进d3.layout.force中nodes和links方法分别为节点和边的数据接口, start函数为布局做准备, 包括数据格式的映射和初始化图元位置, tick函数则使节点在各个作用力下迭代运动直至收敛平衡.
但适用于第三版D3.js力导向图的数据有一定要求, links中传入的关系数据, “source”和“target”字段, 作为连线两端的标识, 必须指向nodes中节点相应索引(从0开始的连续整数, 或者nodes对象的属性名), 并不能依据用户指定的字段而建立边与点之间的映射关系. 由于索引的连续性, 添加或删除某节点, 会影响其后所有节点的索引, 进而影响相关连线两端的标识. 文献[13]中所提到的代码方式, D3.js本身并不能通过迭代自动建立联系. 基于本文中数据交互较为频繁多变, 每次重新建立索引较为繁琐且易出错, D3原来的数据结构无法有效处理数据, 故改进D3.js源码, 使d3.layout.force迭代关联数据时, 判断relevance指向关系, 实现边-节点间的映射关系可自定义化, 即可指定节点的某一特征或属性建立关联, 灵活且直观, 同时也便于开发过程中的调试. start函数建立映射部分改进的核心代码如下:
force.start = function() {
…
for (i = 0; i < links.length; ++ i) {
o = links[i];
//默认关系指向, 依索引建立映射
typeof o.source == "number" && (o.source = nodes[o.source] );
typeof o.target == "number" && (o.target = nodes[o.target] );
// relevance定义映射关系
typeof o.source == "string" && (o.source = findNode(nodes, o.source, o.relevance) );
typeof o.target == "string" && (o.target = findNode(nodes, o.target, o.relevance) );
…
}
…
}
findNode = function(nodes, nodeFlag, relevance) {
for (var i = 0; i < nodes.length; i++) {
if( nodes[i][relevance] && nodes[i][relevance] == nodeFlag) return nodes[i];
}
}
改进后的D3.my.js, 保留D3.js原始的边-节点之间的关系, 即默认情况(不指定关联字段)仍由节点索引建立关联. 指定关联属性的情况下, 可根据指定属性建立关联. 示例如下:
节点数据:
nodes={['name': '李某', 'id':'u235654'],
['name':'张某', 'id':'u364354'],
['name':'周某', 'id':'u46356']};
d3.v3.js原始关联关系的关系数据:
links={['source': 0, 'target': 2, 'relation':'好友'],
['source': 0, 'target': 1, 'relation':'同学'],
['source': 1, 'target': 2, 'relation':'夫妻']}
改进后关系数据:
links={['source': u235654’, 'target': u364354’,
'relevance':'id', 'relation':'好友'], //id关联
['source': '李某', 'target': '张某',
'relevance':'name', 'relation':'同学'], //name关联
['source': 1, 'target': 2, 'relation':'夫妻']} //默认索引关联
可见改进后的关联关系更加直观且灵活, 但需注意的是关联属性值须具有唯一性.
力导向布局的迭代运动过程, 每次位移重绘消耗较大, 依D3的布局收敛条件, 会存在冗余震荡, 即后期较多时间的运动对布局无明显效果, 本文在无明显布局误差的情况下, 限制迭代次数.
对改进前后性能进行了对比验证, 以chrome52浏览器作为验证工具, 改进前后的布局准备before-start、after-start耗时和布局总耗时before-end、after-end如图2所示, 其中end与start的差为布局迭代运动重绘耗时.
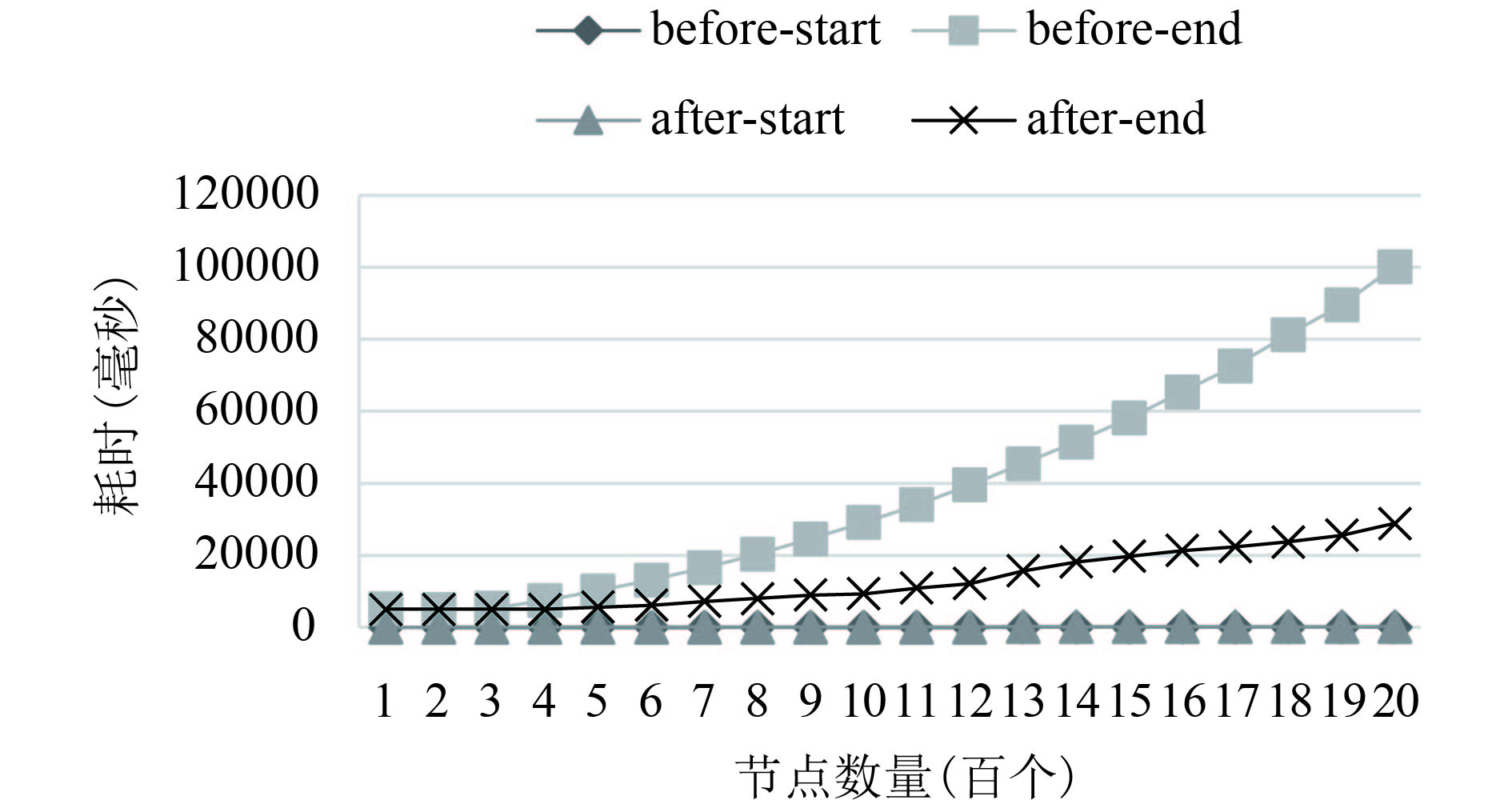
|
图 2 改进前后性能对比 |
由上图不难发现, 随节点数量的增加, 改进前, 力导向布局迭代的时间消耗急剧增加, 改进后的布局迭代耗时增长缓慢很多, 性能有明显改善. 改进前后, 数据准备阶段耗时几乎一致, 说明指向关系的改进在没有增加额外消耗的情况下, 增强了D3库的可用性.
3 人物关系可视化设计 3.1 整体架构根据CARD可视化模型可以将信息可视化的过程分为以下几个阶段: 数据预处理, 绘制、显示和交互[14]. 传统可视化模型又叫流水线模型, 缺陷是未考虑用户交互需求, 可视化回路模型[15], 解决了用户交互的问题, 使用户对于数据的挖掘和了解有了更多可能性, 但频繁的前后台的交互操作加大了系统的开销. 王子毅等提出的Drilldown模型[15]较好的解决了这个问题, 但该文基于Echarts的实现过于复杂. 而D3恰好具有良好的数据驱动特性, 可以不需要过于复杂的处理而实现高性能交互.
本文根据人物关系可视化的实际业务需求, 采用Tomcat 7.x作为服务器, Oracle 11g作为数据库, 后台采用Java编写, 前端应用Html、JavaScript、compass等技术, 实现人物关系的图谱展示, 并实现一定的基于数据的交互功能. 系统的框架描述如图3.
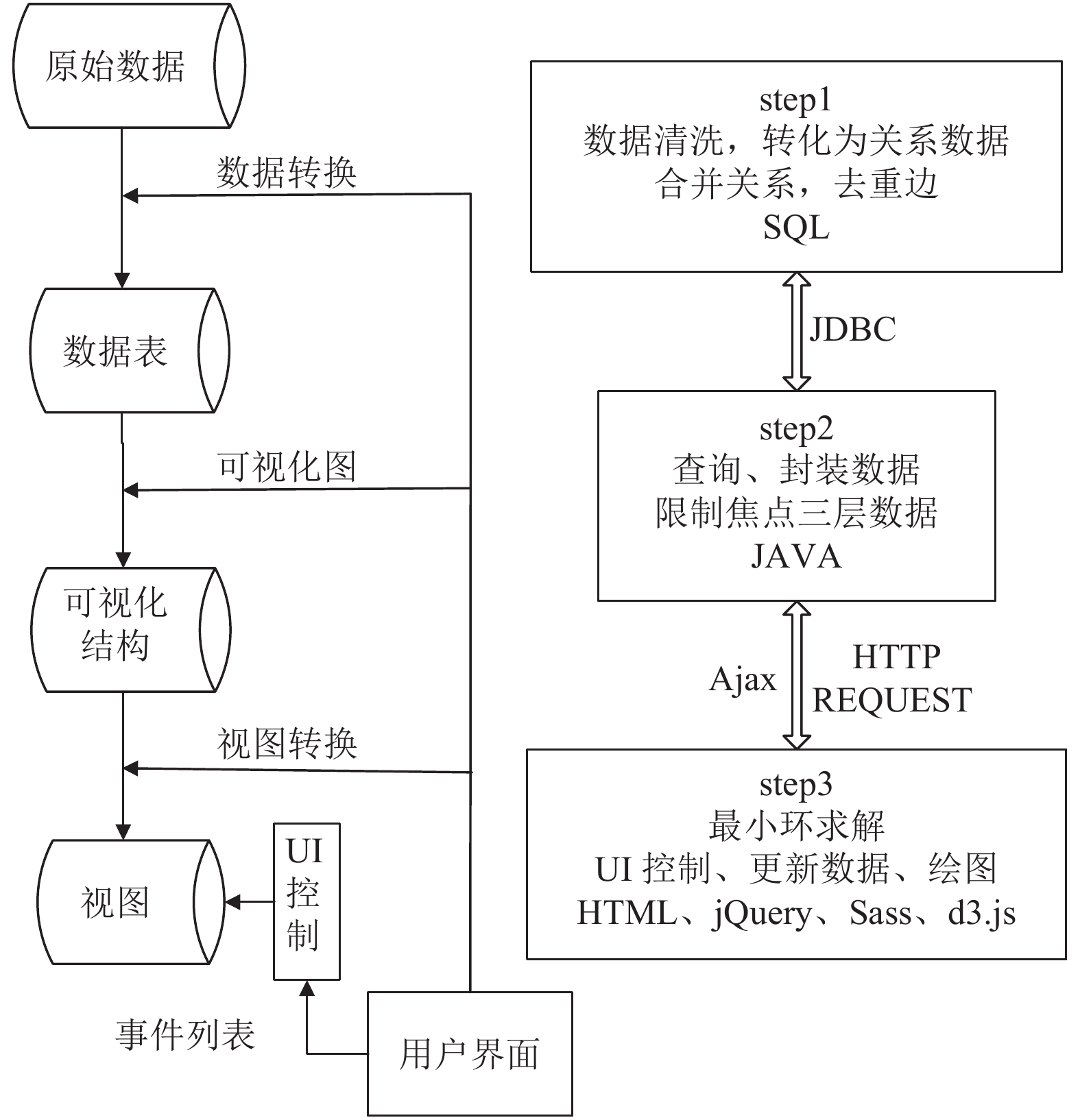
|
图 3 系统框架流程 |
信息可视化过程中, 依据数据的转换可划分为: 原始数据到数据表、数据表到可视化结构、可视化结构到视图的三个转换过程.
数据交互中, 一部分交互是基于前端后台的, 应用Ajax异步传输数据, 完成前后台的数据交互, 如通过人员ID搜索人物关系; 另一部分交互则是利用d3.js的数据驱动特性, 使得可以不向后台发送http请求而获取到相应数据, 如鼠标单击人物节点进行详情展示, 回调函数直接调取节点数据, 大大减小服务器端负担, 缩减了响应时间, 提高了用户体验效果.
3.2 数据处理(1)亲密度
引入亲密度, 量化描述人物间的关系, 考虑联系类型(书信、电话、邮件、在线聊天工具等)和互动次数两个维度, 亲密度定义(依据不同业务需求, 可调整)如式(1).
| $Intimacy(u,v){{ = }}\sum\limits_i {{w_i}{I_i}} (u,v)$ | (1) |
其中Intimacy(u, v)表示u和v之间的亲密度, wi为联系类型i的权重, Ii(u, v)为u、v以i方式进行交互联系的总次数. 为便于定量筛选, 式(2)将亲密度量化至0~100.
| $Intimacy(u,v){{ = }}\frac{{Intimacy(u,v) - {{MIN}}}}{{MAX - MIN}} \times 100$ | (2) |
MAX和MIN分别为亲密度的最大和最小值.
另外, 本文中的人物关系实际上是混合图, 既有有向边(如父子关系)又有无向边(如好友关系), 且存在重边(两人间可能存在多种关系, 如既是母女关系又是师生关系). 本文在数据处理中合并重边, 依赖亲密度大小排序, 标识所有关系, 以最大亲密度作为合并亲密度, 将混合图简化为无向简单图.
(2)数据库设计
张运良[16]将关系和节点存储在一张表中, 由于节点数据的重复, 会造成大量的数据冗余, 且不便于数据更新, 本文将关系和节点信息分存于两张表中, 以用户ID作为关联信息.
本文中数据库共设计两张表nodes和relation, 分别用于存储人物信息和人物间的关系信息, 部分字段及数据如表1和表2所示.
| 表 1 人物节点nodes表的部分字段 |
| 表 2 关系节点relation表 |
(3)多最小环模块
运用第1节的经指定顶点的无向图多最小环算法, 标识当前界面中的团体关系, 采用流程如图4.

|
图 4 最小环数据处理模块 |
当界面中显示图的内容发生变化时, 需要计算或者重新计算, 将当前节点数据nodes和关系数据links作为最小环模块的输入. 递归去除度不大于1的点及与其相连的边, 得到预处理后的数据nodes’和links’. 对节点进行编号, 初始化邻接矩阵, 利用无向图多最小环算法计算最小环路径集合. 最后通过编号映射回节点和边的数据, 更新视图对应边的stroke-width属性, 以达到标识团体关系的目的.
3.3 视图交互为了开发思路清晰, 便于后期维护, 前端视图逻辑共分四个模块D3、relation、circle、index, 每个模块封装为一个Object, 以require.js管理模块依赖, 便于各个模块间的相互调用.
relation.draw() 调用d3.layout.force(), 使用力导向布局, 传入nodes、links数据以及size、linkDistance、charge等参数, 使图元与数据建立映射关系, D3通过执行映射规则, 将抽象数据转为直观图像. 以<g>分组不同语义的svg元素, 便于不同视图元素的层级设置, 定义各元素的事件回调, 完成画图及界面事件监听功能. relation.update()接受新的数据, 更新视图.
人物信息按照用户关注程度, 分为三个等级, 关系图通过交互形式实现信息的多级钻取, 呈现于不同位置: 关系图节点处标识核心信息, 悬浮框显示次要信息, 个人档案页显示人员全量信息.
不同于文献[16]的动态交互, 点击节点查询为关系扩展, 而非另一个初始查询, 避免频繁移焦而使用户失去方向. 同时本文做了关系层级限制, 通过限制当前显示信息量, 以减少感知超载问题, 将关系限制在以中心人员为中心的三层关系内.
鼠标悬浮于人物节点时, 交互响应行为为该节点放大并且沿线显示与该节点直接相关的关系描述标签; 双击该节点实现关系拓展; 单击弹出详情悬浮框; 拖拽节点后可重新布局. 其中, 对于浏览器来说, 双击操作会触发两次单击事件, 本文采用设定定时器的方式来判定区分用户端的单击和双击操作.
4 实现本文通过编码, 对以上理论进行实践, 效果展示如图5至图10.
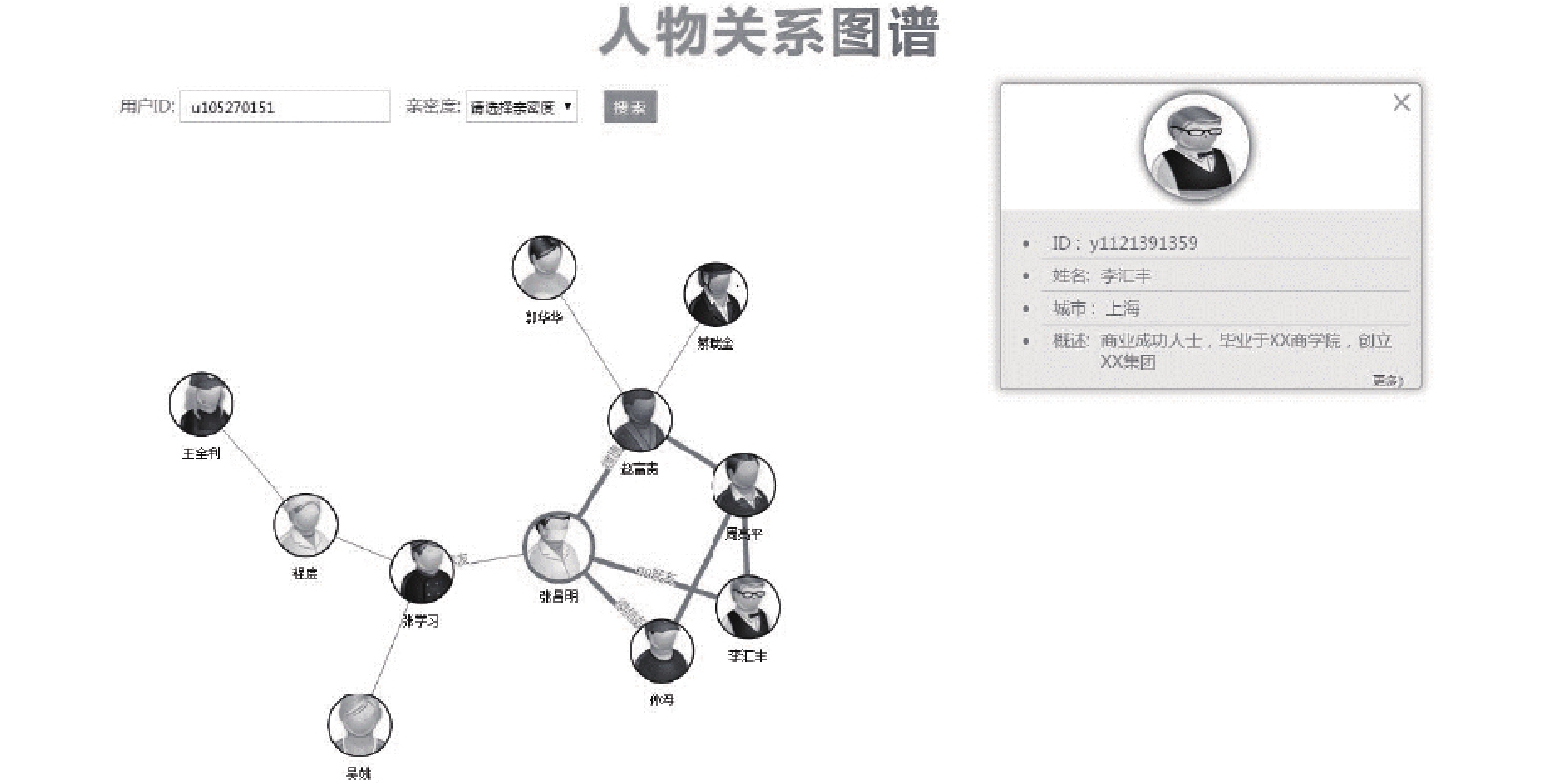
|
图 5 人物关系图整体界面 |
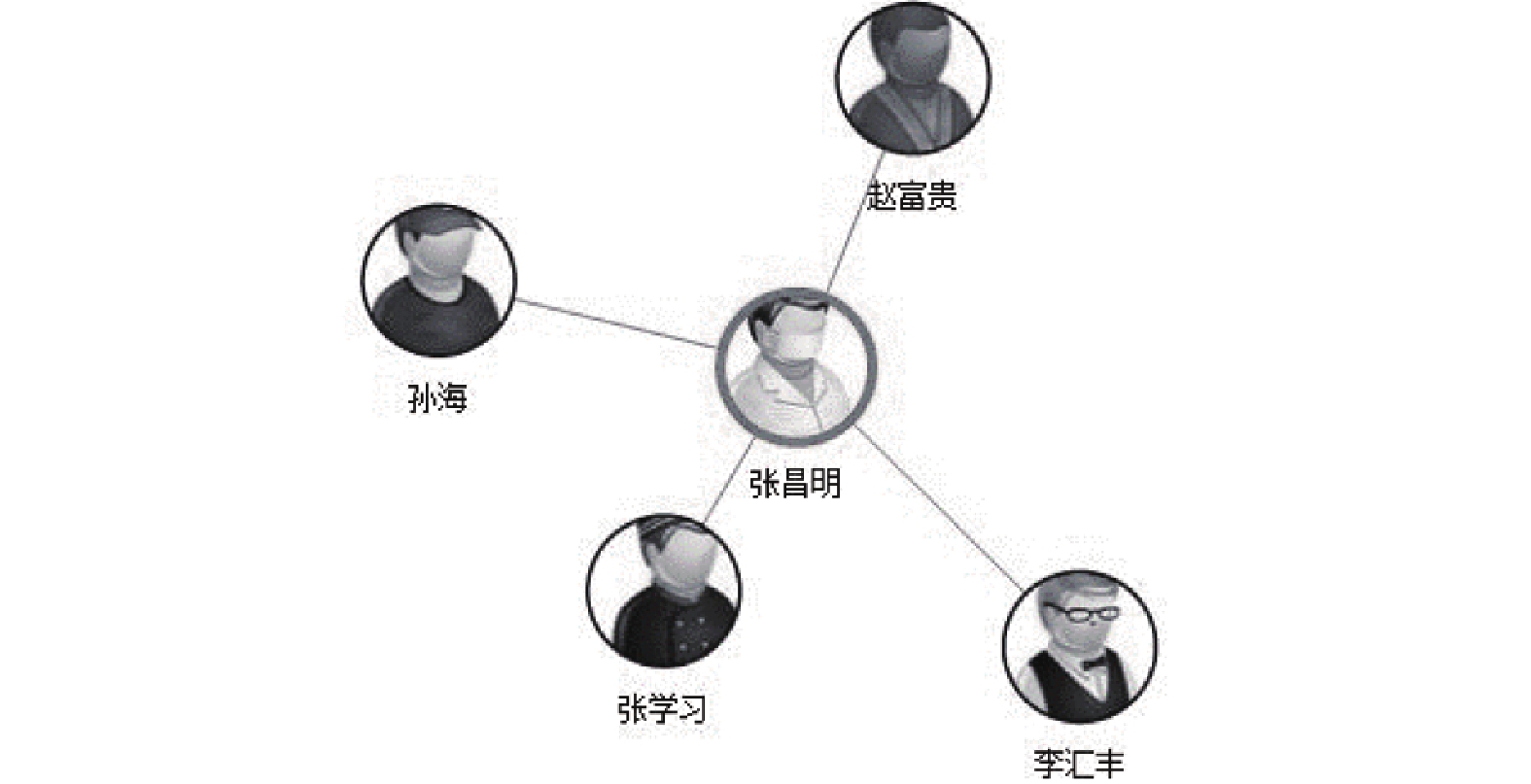
|
图 6 根据ID查询关系 |
图5为人物关系可视化整体界面, 分为查询区、视图区、人物卡片区(提供档案页入口), 鼠标悬浮某节点可沿连线方向显示关系描述; 图6为查询某ID后的结果, 视图节点处显示人物图片和姓名, 中心人物有视觉突出效果; 图7为对图2结果集进行亲密度过滤后的结果; 图8是双击人物节点后拓展关系; 图9中则是计算当前视图中包含中心节点在内的所有最小环, 通过连线加粗的方式标识了人物间的团体关系; 图10为单击节点后, 以悬浮框的形式显示人物详情, 并提供人员档案的入口.
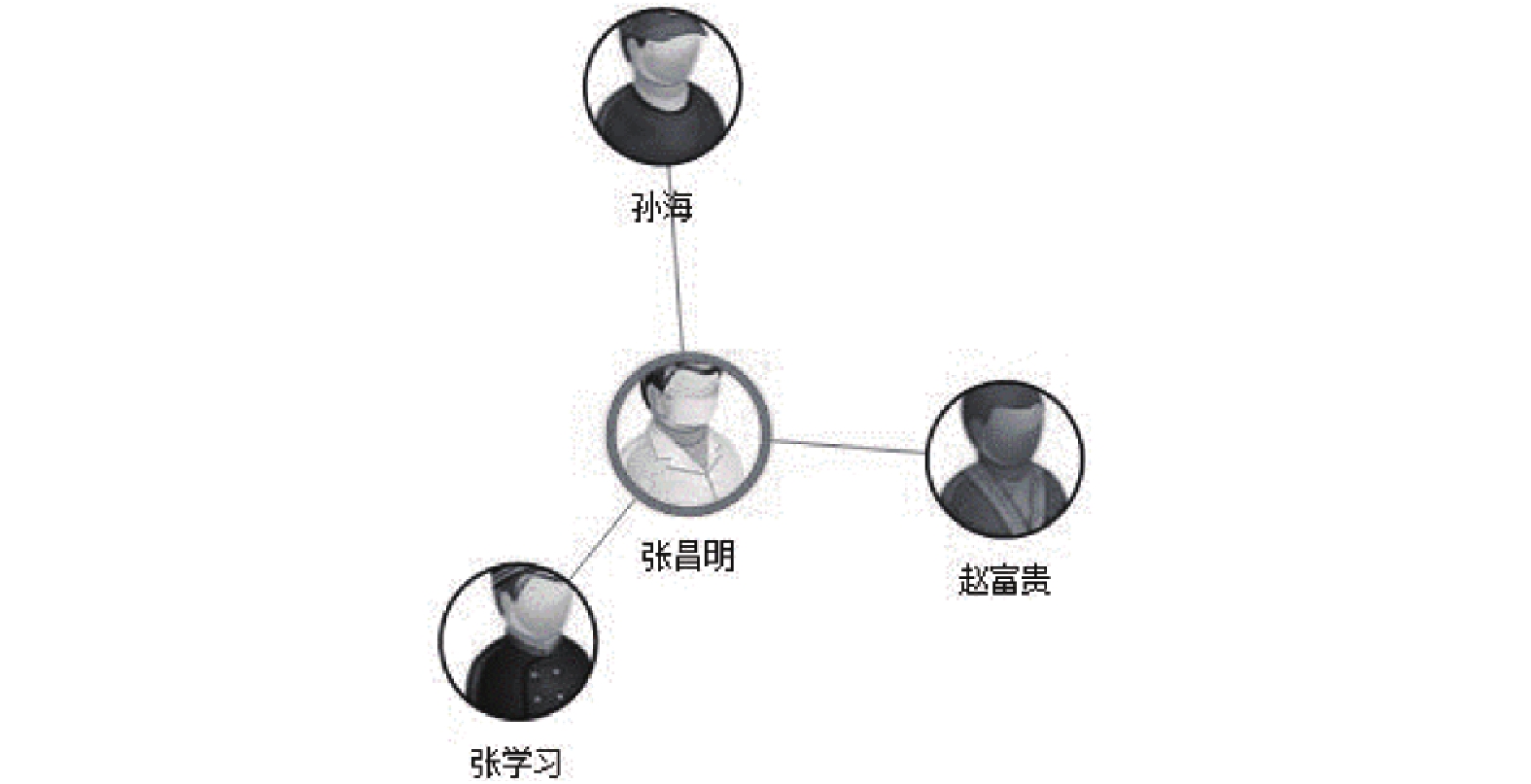
|
图 7 亲密度过滤 |
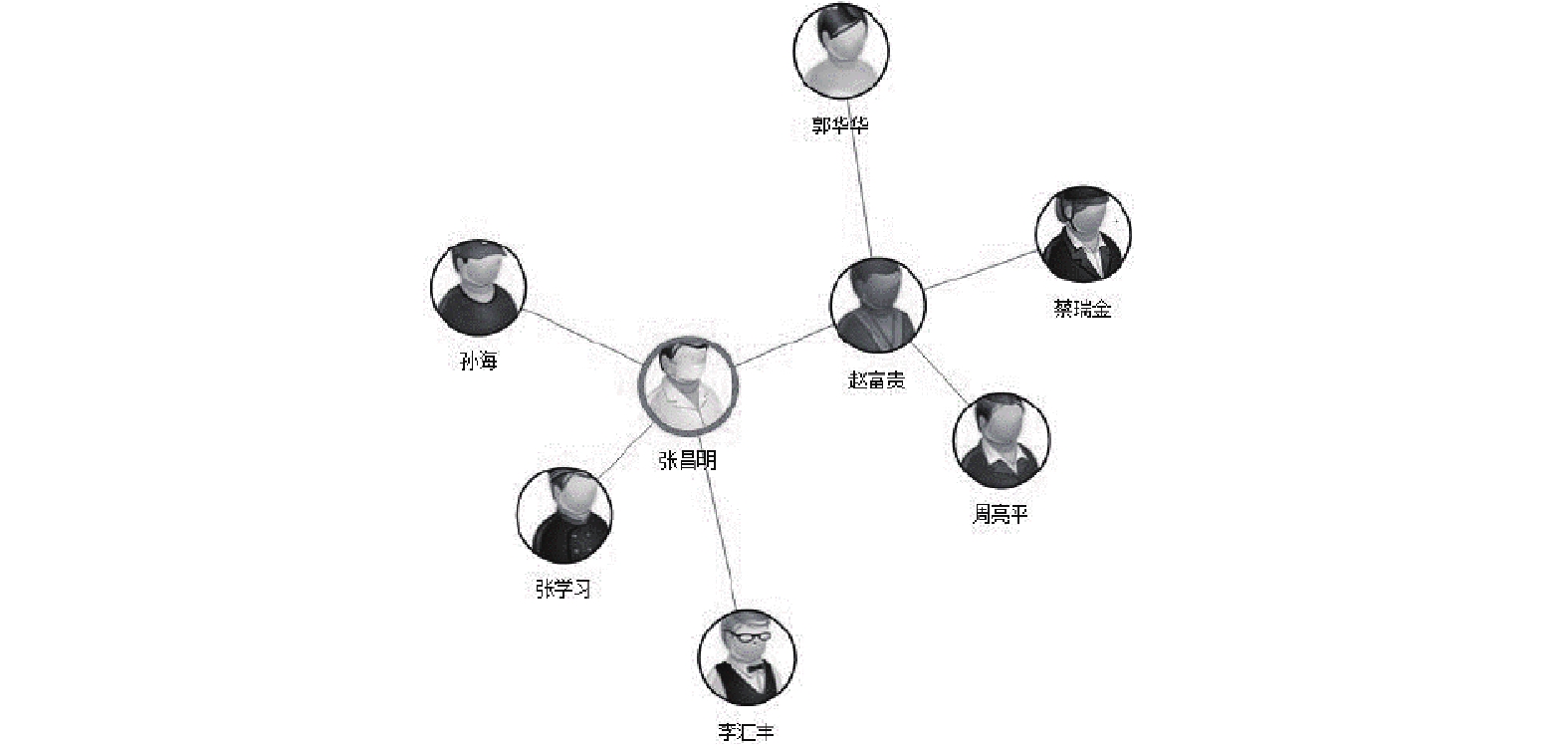
|
图 8 关系拓展 |
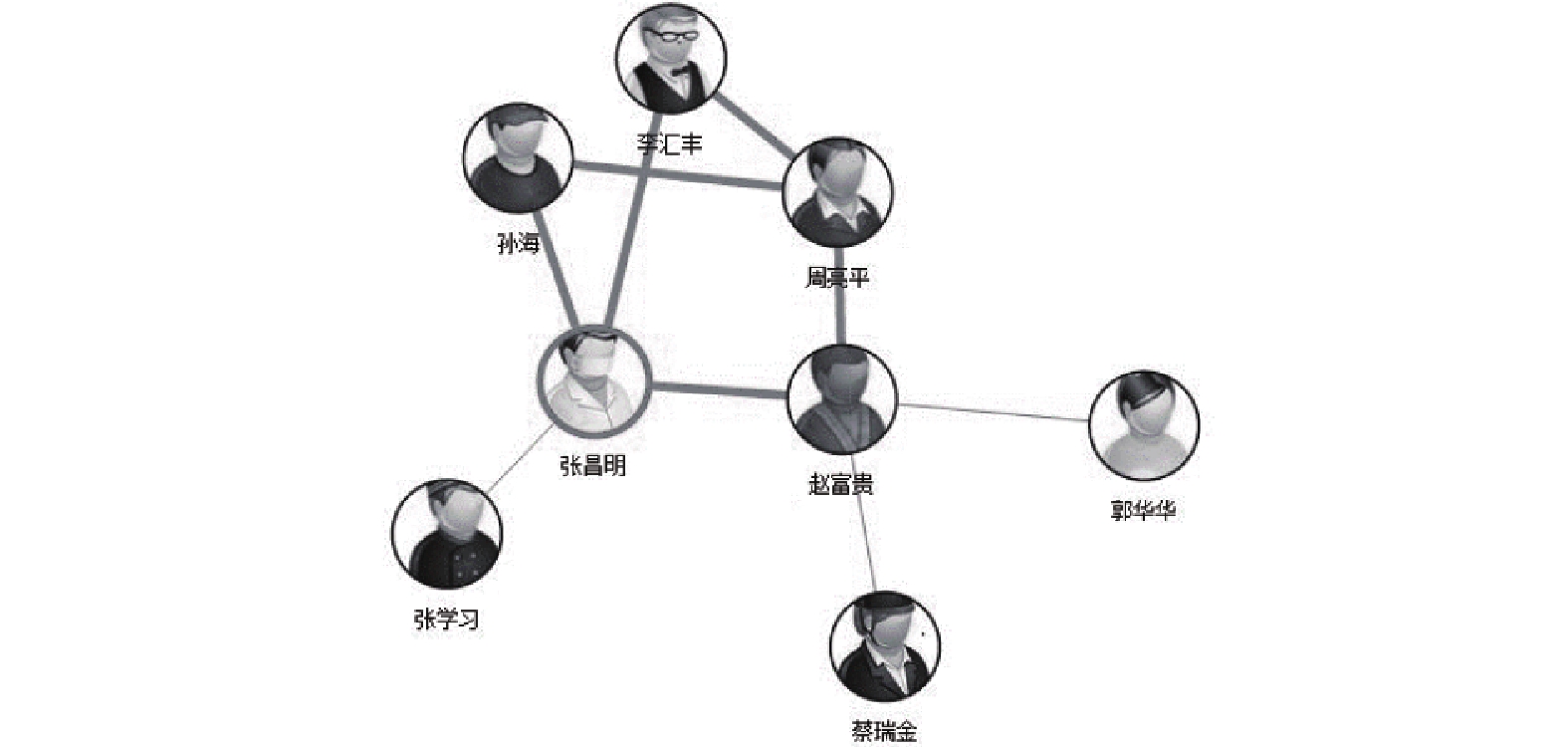
|
图 9 最小环团体 |

|
图 10 详情悬浮框 |
以6组不同数据验证人物关系可视化系统, 结果如表3.
表3中, 实验1与实验2对比, 实验3与实验4对比可证, 最小环处理模块因为对度小于2的点的预处理, 求解过程耗时较少, 对于相对稀疏的图, 效果明显.
实验3、4与实验6对比, 可见更新后需重新布局的节点个数相当时, 更新节点数较少比更新点数多时, 更新布局耗时较少, 因为图中元素只有少部分的被更新节点附近的点需要移动, 而对大部分节点而言, 更新节点带来的受力变化可以忽略不计或者很小, 经过较少次迭代即可达到收敛条件. 实验5与实验6对比, 剩余点数点数越多, 重新布局越耗时.
5 结论与展望本文深入了解了D3.js的特性和工作机制, 基于改进的D3.js可视化库, 利用力导向合理布局, 实现了动态交互的人物关系可视化原型, 直观、有效地展现人物间的关联关系及团体关系, 以交互的形式实现数据多级钻取, 进一步探索对象相关信息, 满足了动态交互的基本要求. 在以后的研究中, 视图与交互细节, 如视图多样性和图谱的再编辑性等还需做深入探讨和实现.
| 表 3 6组实验结果 |
| [1] |
杨彦波, 刘滨, 祁明月. 信息可视化研究综述. 河北科技大学学报, 2014, 35(1): 91-102. DOI:10.7535/hbkd.2014yx01016 |
| [2] |
赵聪. 可视化库D3.js的应用研究. 信息技术与信息化, 2015(2): 107-109. |
| [3] |
权庆乐, 连卫民. 对可视化库D3.js的应用研究. 电子技术与软件工程, 2014(18): 203. |
| [4] |
权鑫. 基于D3.js的数据可视化系统框架设计与实现[硕士学位论文]. 北京: 北京交通大学, 2016.
|
| [5] |
Craw D, Block J, Lin K, et al. Firemap: A dynamic data-driven predictive wildfire modeling and visualization environment. Procedia Computer Science, 2017, 108: 2230-2239. DOI:10.1016/j.procs.2017.05.174 |
| [6] |
Zou J, Chang Q, Arinez J, et al. Data-driven modeling and real-time distributed control for energy efficient manufacturing systems. Energy, 2017, 127: 247-257. DOI:10.1016/j.energy.2017.03.123 |
| [7] |
王树西, 李安渝. Dijkstra算法中的多邻接点与多条最短路径问题. 计算机科学, 2014, 41(6): 217-224. DOI:10.11896/j.issn.1002-137X.2014.06.043 |
| [8] |
汤志贵. Dijkstra与Floyd在求最小环时其算法优劣比较. 电脑知识与技术(学术交流), 2007(9): 709-711. |
| [9] |
鲍培明. 距离寻优中Dijkstra算法的优化. 计算机研究与发展, 2001, 38(3): 307-311. |
| [10] |
赵礼峰, 梁娟. 最短路问题的Floyd改进算法. 计算机技术与发展, 2014, 24(8): 31-34. |
| [11] |
Bostock M, Ogievetsky V, Heer J. D3: Data-driven documents. IEEE Transactions on Visualization and Computer Graphics. 2011. 2309.
|
| [12] |
Dailey D, Frost J, Strazzullo D. Building web applications with SVG. Sebastopol, California: Microsoft Press, 2012.
|
| [13] |
黄冠华, 杨鹤标. 基于D3.js的微博舆情分析可视化研究. 软件导刊, 2016, 15(6): 142-144. |
| [14] |
陈鹏鹏. 移动互联网下数据可视化技术及应用. 智能计算机与应用, 2015, 5(6): 38-41. |
| [15] |
王子毅, 张春海. 基于ECharts的数据可视化分析组件设计实现. 微型机与应用, 2016, 35(14): 46-48, 51. |
| [16] |
张运良, 张兆锋, 张晓丹, 等. 使用D3.js的知识组织系统Web动态交互可视化功能实现. 现代图书情报技术, 2013, 29(7–8): 127-131. |
 2018, Vol. 27
2018, Vol. 27



